基于直覺模糊的科技型小微企業信用評價

張 笑，吳 堅，曹清瑋

（浙江師范大學 經濟與管理學院，浙江 金華 321004）

基于直覺模糊的科技型小微企業信用評價

張 笑，吳 堅，曹清瑋

（浙江師范大學 經濟與管理學院，浙江 金華 321004）

我國現行的信用評價體系不能準確地評估科技型小微企業的信用狀況。為解決信用評價中的不確定性和模糊性，利用直覺模糊數的多屬性評價方法，構建綜合信用評價指標體系；建立直覺模糊判斷矩陣，利用定性與定量相結合的層次分析法確定評價指標權重，并利用改進的TOPSIS法對方案進行排序。應用實例表明，基于直覺模糊的科技型小微企業信用評價方法計算簡便，評價結果精準科學，具有較好的實用價值。

科技型小微企業；信用評價；直覺模糊數；層次分析法；TOPSIS法

Abstract:China’s current credit evaluation system cannot accurately assess the credit status of SMEs. In order to solve the uncertainty and ambiguity in credit evaluation, the paper employs multi-attribute evaluation method based on intuitionistic fuzzy number to build a comprehensive credit evaluation index system, establishes valued intuitionistic fuzzy judgement matrix with a combination of both qualitative and quantitative methods to obtain subjective weight of attribute, and adopts improved TOPSIS solution for order preference. The application result shows that the calculation of multi-attribute evaluation method based on intuitionistic fuzzy number is simple, its assessment result is more accurate and scienti fi c, and its application value is much better.

Key words:Technology-based SMEs; Credit risk evaluation; Intuitionistic fuzzy number; Analytic hierarchy process; TOPSIS method

0 引 言

科技型小微企業一般都處于初創期或成長期，與處于成熟期的科技型大中企業相比，具有發展時間短、資金規模小、收益不穩定、經營風險高、擔保能力弱等劣勢，不能向銀行和資本市場傳遞有效的“硬信息”，導致其在發展過程中面臨融資的信用障礙[1]。學界從不同角度探討了中小企業信用評價體系或信用評估模型，但都存在以下問題：一是沒有考慮科技型小微企業信用風險評價的模糊性和不確定性。科技型小微企業信用評價需要綜合考慮財務指標（如資產負債率）和非財務指標（如企業領導者素質），而非財務指標往往是不定性的，需要運用不確定決策方法。二是缺乏專門針對科技型小微企業的信用風險評價體系，忽略企業的科研創新能力及發展前景。三是科技型小微企業信用風險的評價方法存在一定的不合理性，如Probit模型、Logit模型、Z-score模型等，雖然結果更為準確，但缺點是過分強調定量分析。模糊評價方法及信用風險度量模型等適用于包含大量定量數據的大中型企業。在信用評價過程中，由于受客觀環境的復雜性、決策者的知識結構和專業水平等諸多因素影響，決策者往往不能提供對決策方案的精確偏好信息，給出的信息存在著一定的猶豫度，具有模糊的特點。Atanassov[2]在對模糊集進行擴展的基礎上提出了直覺模糊集的概念，同時考慮了隸屬度、非隸屬度和猶豫度三方面的信息，在處理模糊性和不確定性等方面與Zadeh的模糊集[3]相比能更細膩、全面地描述客觀現象的自然屬性。本文運用直覺模糊集描述模糊性，可同時表示支持、反對和中立三種狀態，使得在處理不確定信息時具有更強的表現力。同時將直覺模糊集與層次分析法（AHP）相結合，提出一種直覺模糊層次分析法，運用直覺模糊層次分析法表達定性指標的模糊性，并結合TOPSIS法，提出科技型小微企業信用評價決策中相應的評價模型。在商業銀行的科技型小微企業信用評價中，采用直覺模糊層次分析法，為商業銀行提供了一種新的評價方法，能很好地為商業銀行提供貸款決策。

1 相關知識

1.1 直覺模糊集基本理論

定義1[4]假設X是一個論域。若X上兩個映射μA：X→[0, 1]，υA：X→[0, 1]，使得x∈X→μA(x)∈[0, 1]，x∈X→υA(x)∈[0, 1]，并滿足條件0≤μA(x)+υA(x)≤1，則稱μA, υA確定了論域X上的一個直覺模糊集A，可記為A={＜x, μA(x), υA(x)＞|x∈X}，分別稱μA, υA為A的隸屬函數和非隸屬函數，μA(x), υA(x)為元素x屬于A的隸屬度和非隸屬度，稱πA(x)=1-μA(x)-υA(x)為A中元素x的猶豫度。論域X中的元素x屬于A的隸屬度與非隸屬度所組成的有序對稱＜μA(x), υA(x)＞為直覺模糊數[5]，直覺模糊集A可看作是全體直覺模糊數的集合，表示為：A=[＜μA(x1), υA(x1)＞, ＜vA(x2), υA(x2)＞,…,＜ vA(xn), υA(xn)＞]。

定義2[6]13-15假設X是一個非空集合，A={＜x,μA(x), υA(x)＞|x∈X}，B={＜x, μB(x), υB(x)＞|x∈X}均為直覺模糊集，則

A×B={＜x, μA(x) μB(x), υA(x)+υB(x)-υA(x) υB(x) ＞|x∈X }

λA={＜x, 1-(1-μA(x))λ, (υA(x))λ＞|x∈X }

定義3[7]假設A={＜x, μA(x), υA(x)＞|x∈X}和B={＜x, μB(x), υB(x)＞|x∈X}為給定論域X上的兩個直覺模糊集，πA=1-μA(x)-υA(x)，πB=1-μB(x)-υB(x)分別為直覺模糊集A和B的猶豫度，則定義A, B的距離為：

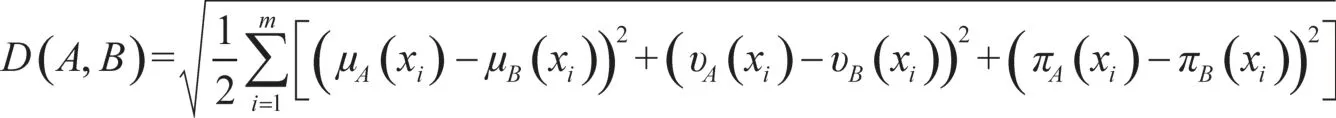
若不同元素具有不同的權重，其加權距離為：

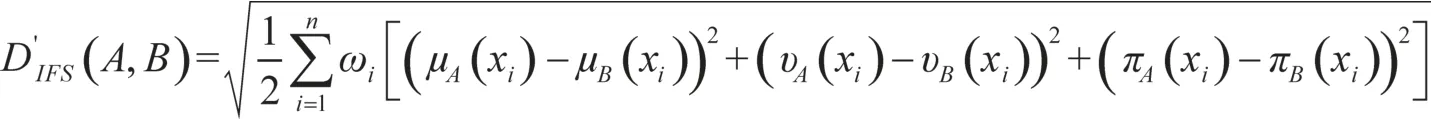
其中ωi為xi的權重，滿足

1.2 TOPSIS原理

TOPSIS法是C. L. HWang等為解決單個決策者的多屬性決策問題，于1981年最先提出來的一種接近于線性加權平均方法的排序法，其基本思想是：所選擇的滿意方案應盡可能地接近正理想解，同時又盡可能地遠離負理想解[8]。正理想解是一個虛擬的最優解，其各個指標值都達到評價對象中的最優解；負理想解是虛擬的最差解，其各個指標都達到評價對象中的最差值。在原有的方案中一般不存在正理想解和負理想解，可把每個實際的方案與正理想解和負理想解作比較，若其中有一個方案最接近正理想解，同時又遠離負理想解，則該方案就是最優解。

定義4[6]59-60假設直覺模糊集A的正理想解和負理想解分別為A+和A-，則其直覺模糊集向量分別為：

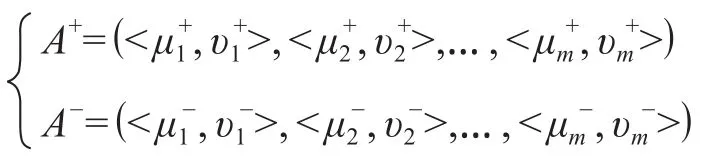
2 科技型小微企業信用評價指標體系的構建

2.1 建立評價指標體系

目前，我國現行信用評價指標體系缺乏對現金流量、企業科研創新能力、履約狀況的分析，不夠重視企業的信用品質，過分依賴定量指標。為解決現行評價指標體系存在的不足，借鑒國內外學者研究成果，同時考慮科技型小微企業的創新性、發展潛力等定性指標，構建由6個一級指標、16個二級指標組成的科技型小微企業信用評價指標體系（見表1）。

2.2 確定評價指標權重

就表1設定的評價指標，對國內信貸領域的20名專家開展了問卷調查，考慮到評價指標權重確定過程中存在的不確定性，采用定性與定量相結合的層次分析法來確定權重[9-11]。以科技型小微企業償債能力指標為例，利用MATLAB計算得到其權重（見表2）。

同樣，采用上述方法計算各指標單層權重并進行一致性檢驗，得到科技型小微企業信用評價指標各單層權重和最終權重（見表3）。

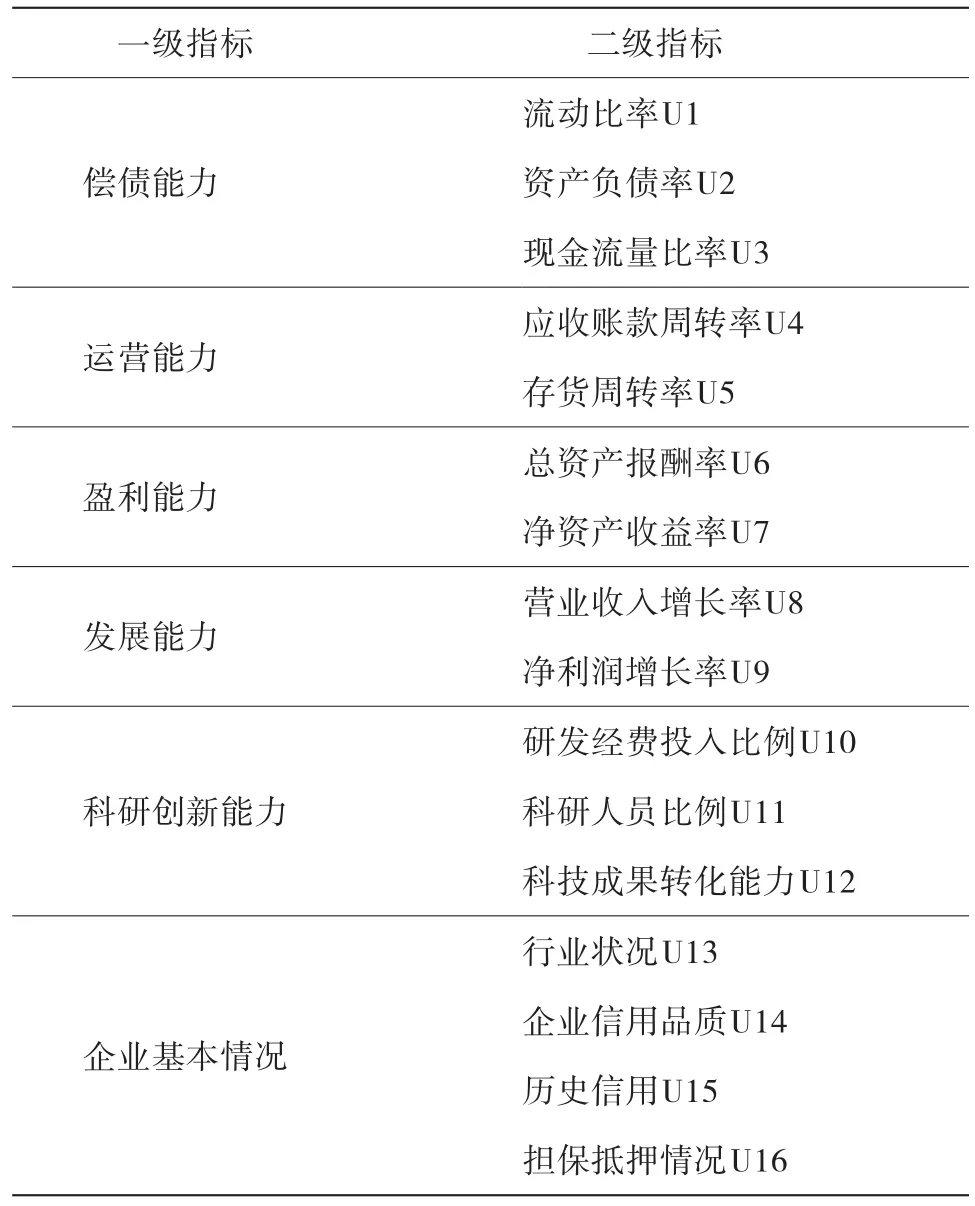
表1 科技型小微企業信用評價指標體系

表2 科技型小微企業償債能力指標單層權重

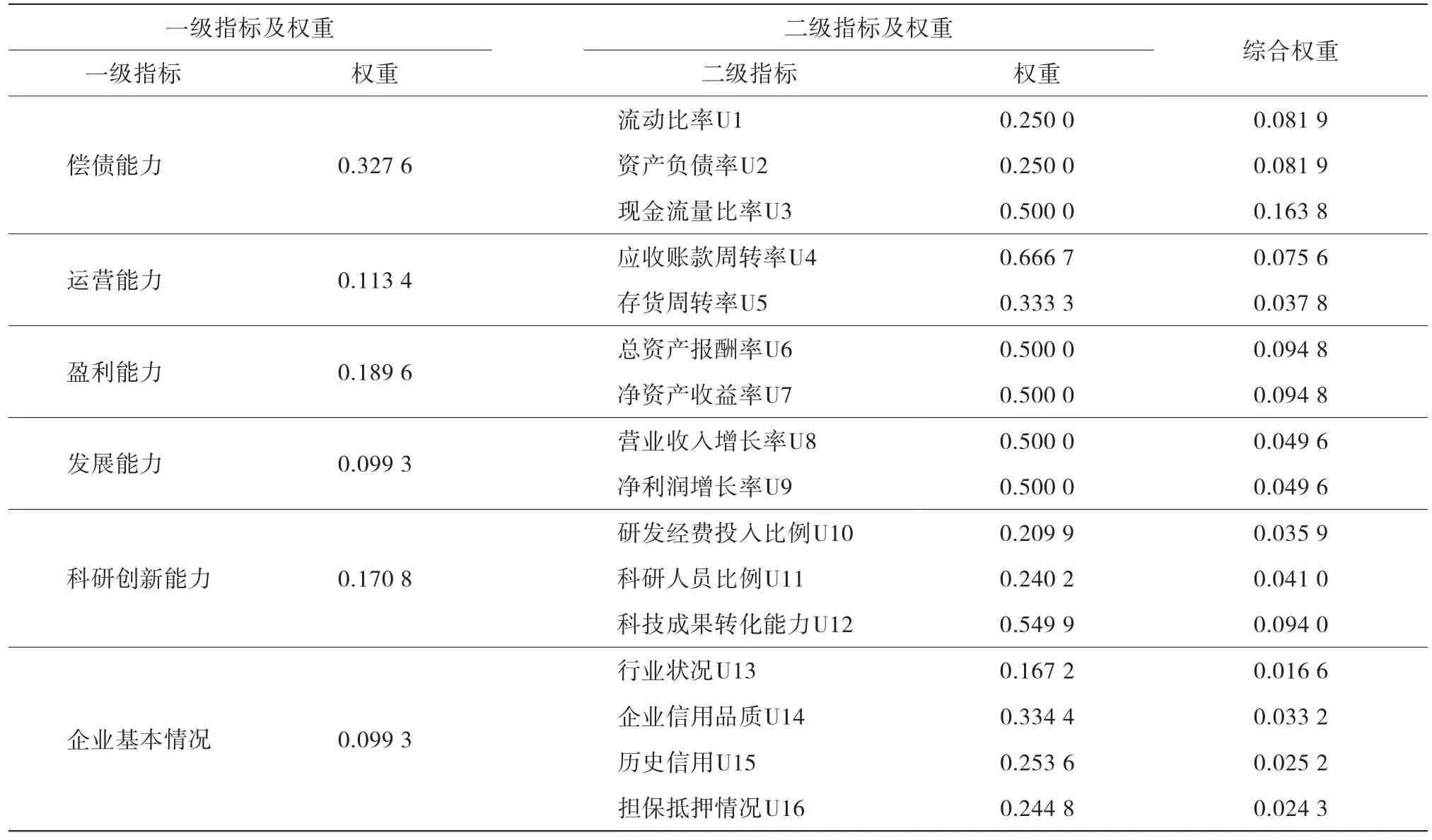
表3 科技型小微企業信用評價指標權重

3 基于直覺模糊的科技型小微企業信用評價方法

現有n個可行方案xj( j=1, 2, …, n)組成方案集X=，由K個專家P(K)組成一個決策群體，對每個方案關于m個屬性oi( i=1, 2, …, m)進行評價，記屬性集為O={o1, o2, …, on}。假設專家Pk對方案xj關于屬性oi的評價值可表示為直覺模糊集于是，專家Pk對方案xj關于所有m個屬性的評價結果可用向量表示為[6]164-168：

從而直覺模糊集多屬性群體問題可用矩陣記為：

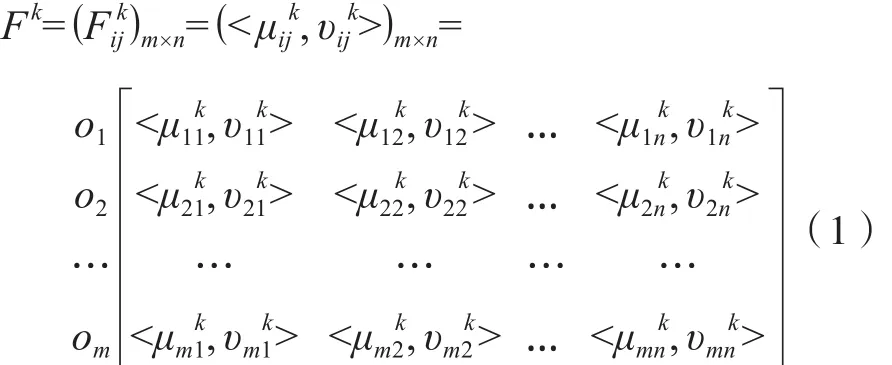
給定所有m個屬性的權重矩陣表示為ωi= (ω1, ω2,…, ωm)T(i=1, 2, …, m)，利用定義2和直覺模糊集決策矩陣Fk( k=1, 2, …, K)，直覺模糊集權重向量ωi( i=1, 2,…, m)，可得到每個決策者Pk的加權直覺模糊集決策矩陣為：

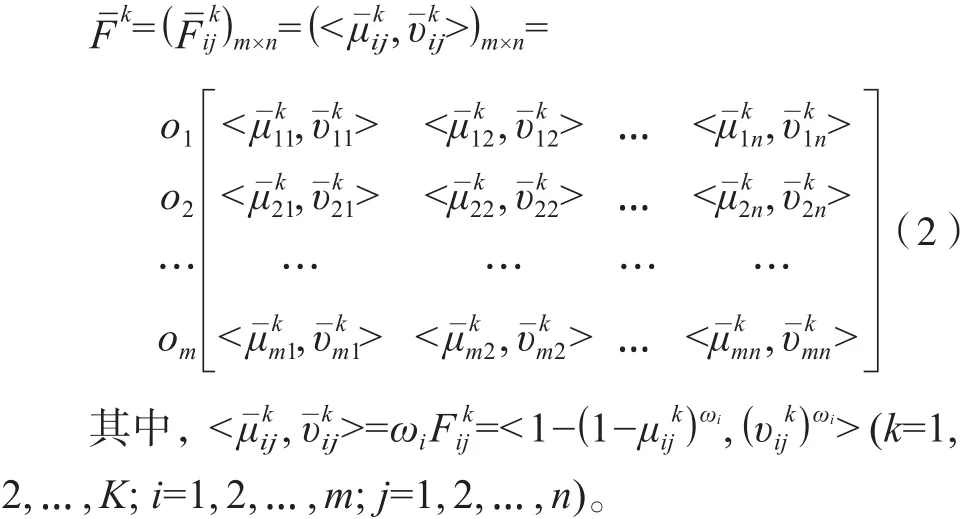
定義決策者Pk的直覺模糊集正理想解xk+和負理想解xk-，其直覺模糊集向量分別為：

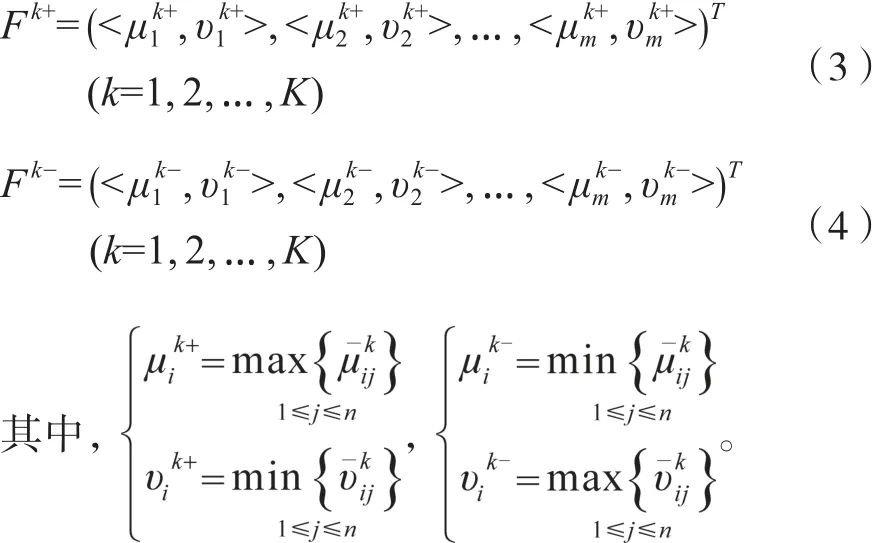
將決策者Pk( k=1, 2, …, K)關于方案xj∈X ( j=1, 2,…, n)與直覺模糊集正理想解xk+和負理想解xk-的歐幾里得距離分別定義為：

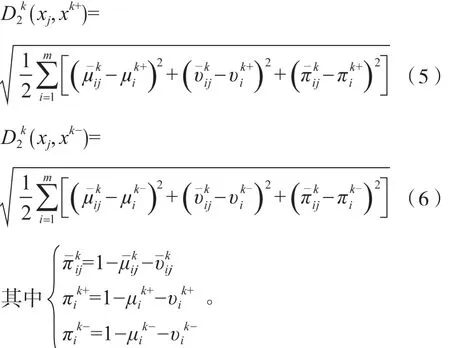
就決策者Pk而言，定義方案xj∈X ( j=1, 2, …, n)與直覺模糊集正理想解xk+的相對接近度為：

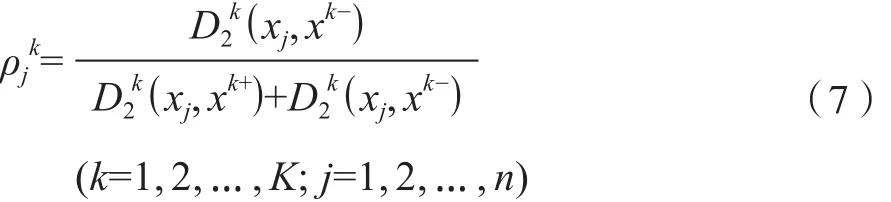
顯然，0≤ρjk≤1，且ρjk越大，其相應的方案越優。

由于在決策群體中有K個決策者并有n個方案，因而可得K×n個相對接近度ρjk(k=1, 2, …, K; j=1, 2, …,n)。把每個決策者Pk(k=1, 2, …, K)看作“屬性”，仍記為Pk，則此時的決策問題可看作是n個方案K個屬性的多屬性決策問題，其中方案xj∈X ( j=1, 2, …, n)關于“屬性”Pk(k=1, 2, …, K)的優屬度為（6）式確定的相對接近度ρjk(k=1, 2, …, K; j=1, 2, …, n)，用矩陣形式記為：

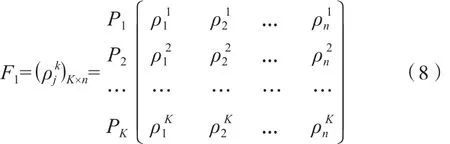
其中F1簡稱為相對接近度決策矩陣。

考慮到不同的決策者可能具有不同的權重，因而假設決策者Pk(k=1, 2, …, K)的權重為ωk(k=1, 2,…, K)，滿足規范化條件：ωk∈[0, 1] (k=1, 2, …, K)，表示決策者的權重向量，可得到加權相對接近度決策矩陣為：

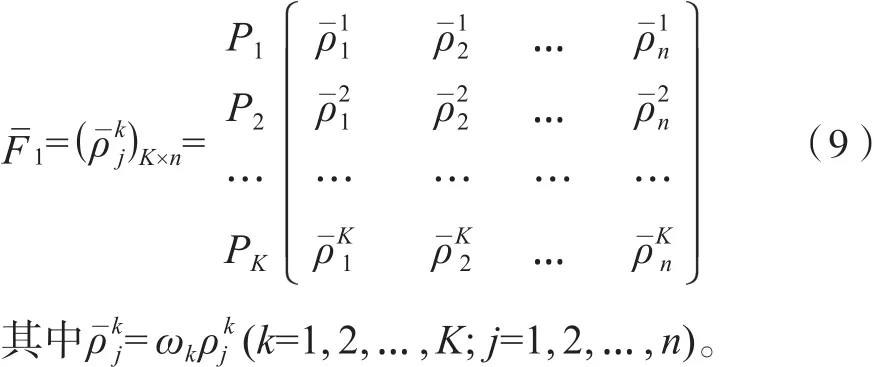
類似地，可定義決策群體的正理想解x+和負理想解x-，其加權相對接近度向量分別為：

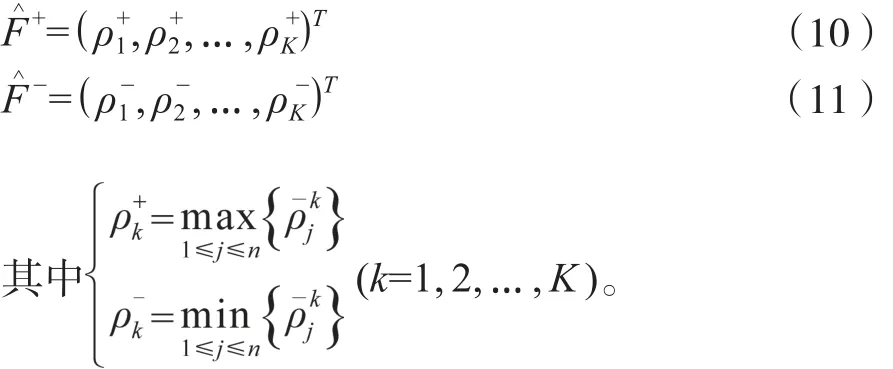
把方案xj∈X ( j=1, 2, …, n)與決策群體的正理想解x+和負理想解x-的歐幾里得距離分別定義為：

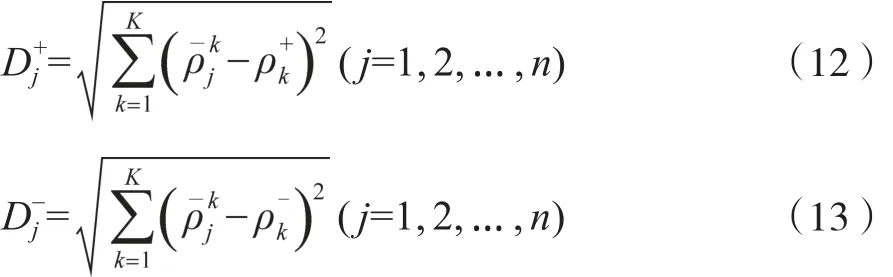
計算方案xj∈X ( j=1, 2, …, n)與決策群體的正理想解x+的相對接近度為：

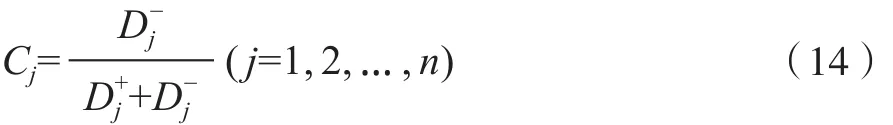
顯然，Cj∈[0, 1] (j=1, 2, …, n)，且Cj越大，則方案xj∈X ( j=1, 2, …, n)越優。根據相對接近度Cj(j=1,2, …, n)從大到小的順序，可確定方案X={x1, x2, …,xn}的優劣排序，并確定其滿意方案。

綜上所述，直覺模糊集多屬性群體TOPSIS法決策過程步驟如下：

（1）識別、確定方案集X={x1, x2, …, xn}，屬性集O={o1, o2, …, om}和決策者Pk( k=1, 2, …, K)。

（2）確定決策者Pk的直覺模糊集決策矩陣Fk和直覺模糊集權重向量ωi( ω1, ω2, …, ωk)T。

（3）利用（2）式計算決策者Pk的加權直覺模糊集決策矩陣。

（4）利用（3）、 （4）式確定決策者Pk的直覺模糊集正、負理想解。

（5）對每個決策者，利用（5）、 （6）式計算方案xj與直覺模糊集正、負理想解的歐幾里得距離。

（6）對每個決策者Pk，利用（7）式計算方案xj與直覺模糊集正、負理想解的相對接近度。

（7）確定決策者的權重向量ω= (ω1, ω2, …, ωK)T。

（9）利用（10）、 （11）式確定決策群體的正、負理想解。

（10）利用（12）、 （13）式計算方案xj與決策群體正、負理想解的歐幾里得距離。

（11）利用（14）式計算方案xj與決策群體正理想解的相對接近度Cj。

（12）根據Cj的不增順序確定方案集X的優劣排序和最滿意的方案。

4 應用實例

表4 專家對方案屬性的評估

根據表3、表4的數據，利用（2）式計算得到3個加權直覺模糊集決策矩陣（見表5）。

利用（3）、 （4）式確定決策者Pk(1, 2, 3)的直覺模糊集正理想解xk+( k=1, 2, 3)和負理想解xk-( k=1, 2, 3)。對每個決策者Pk(1, 2, 3)，利用（5）、 （6）式計算得到方案xj( j=1, 2, 3)與直覺模糊集正理想解xk+( k=1, 2, 3)和負理想解xk-( k=1, 2, 3)的歐幾里得距離（見表6）。

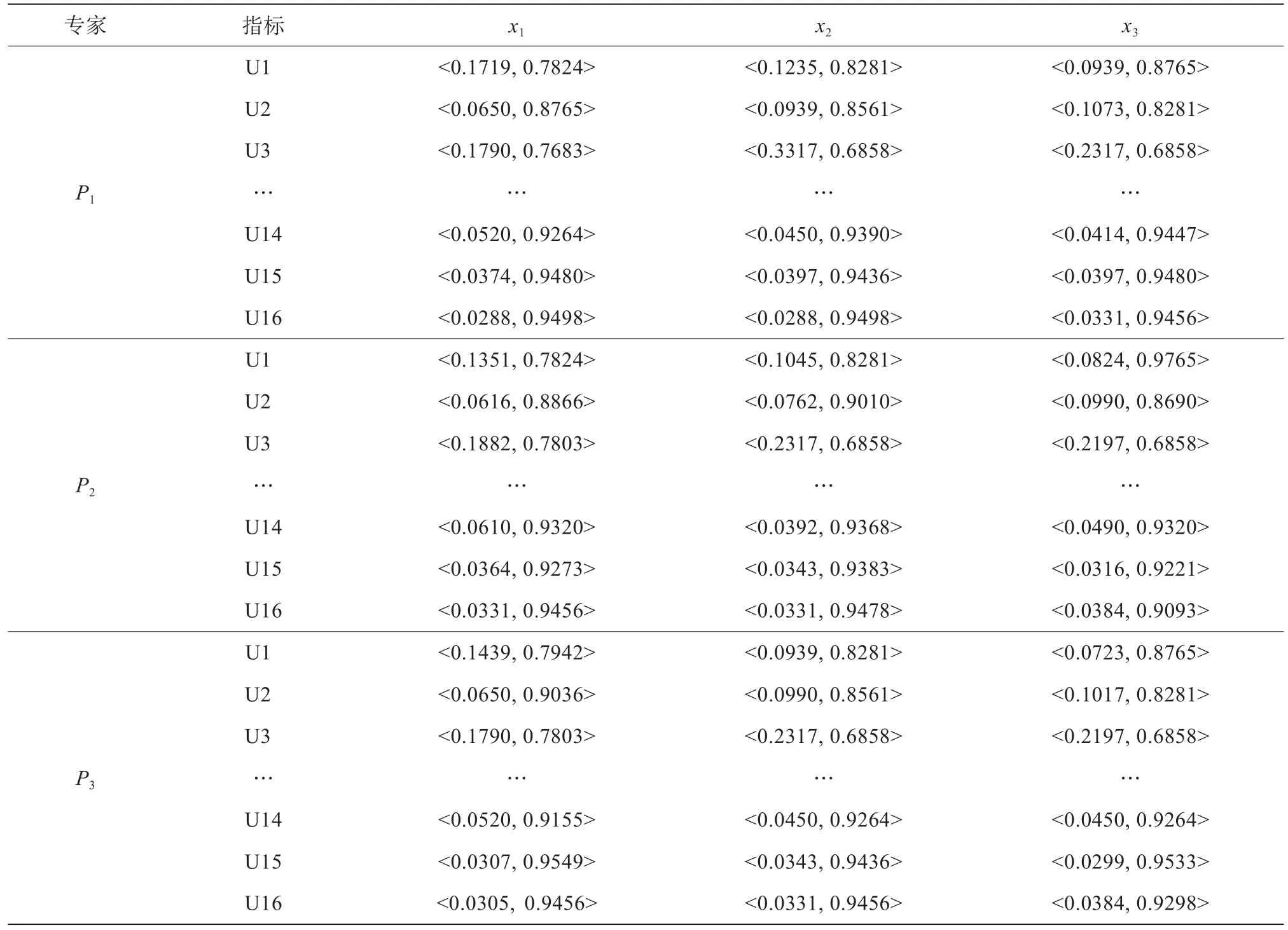
表5 加權直覺模糊集決策矩陣

表6 各方案與直覺模糊集正、負理想解的歐幾里得距離

對每個決策者Pk(1, 2, 3)，利用（8）式計算得到方案xj( j=1, 2, 3)與直覺模糊集正理想解xk+( k=1, 2, 3)的相對接近度決策矩陣為：

根據決策者的工作經驗與實際水平，確定3個決策者Pk(1, 2, 3)的權重向量為ω= (0.4, 0.4, 0.2)T。

利用（9）式計算得到決策群體的加權相對接近度決策矩陣為：

根據（10）、 （11）式，并結合1，確定決策群體的正理想解xk+和負理想解xk-，其加權相對接近度向量分別為：

F^+= (0.2460, 0.2221, 0.1162)T

F^-= (0.1589, 0.1734, 0.0877)T

利用（12）、 （13）式計算得到方案xj( j=1, 2, 3)與決策群體的正理想解x+和負理想解x-的歐幾里得距離分別為：D ( x1, x+)=0.0078，D ( x2, x+)=0.0917，D ( x3,x+)=0.0937，D ( x1, x-)=0.1004，D ( x2, x-)= 0.0487，D ( x3,x-)=0.0122。

根據（14）式計算得到方案xj( j=1, 2, 3)與決策群體的正理想解x+的相對貼近度分別為：C1=0.9275, C2=0.3469, C3=0.1148。

由此可知，3家科技型小微企業信用狀況的優劣排序為x1＞ x2＞x3，且x1為最滿意方案。

5 結束語

本文在分析科技型小微企業特點的基礎上，構建了由企業的償債能力、運營能力、盈利能力和發展能力等財務指標及企業狀況、創新能力、發展潛力等非財務指標構成的科技型小微企業信用評價體系，利用模糊集理論對評價體系中各個指標進行處理，將直覺模糊集與層次分析法相結合，使評價指標權重更合理，增加了模型在描述科技型小微企業信用狀況方面的能力，同時將TOPSIS法引入科技型小微企業信用評價中，使評價結果精準科學。應用實例表明，基于直覺模糊的科技型小微企業信用評價方法計算簡便，評價結果合理性高，具有較好的應用價值。

[1] 趙玲，賀小梅．杭州市科技型小微企業金融服務體系研究—政府促進與市場化的結合[J]．未來發展，2016（12）：38-39．

[2] ATANASSOV K T．Intuitionstic fuzzy Sets[J]．Fuzzy Sets and Systems，1986，20（1）：87-96．

[3] ZADEH L A.Fuzzy Sets[J].Information and Control，1965，8（3）：338-353．

[4] ATANASSOV K T.Intuitionistic Fuzzy Sets[M].New York：Physica-Verlag Heidelberg，1999.

[5] GAU W L，BUEHRER D J.Vague Sets[J].IEEE Transaction on System，Man and Cybernetics，1993，23（2）：610-614．

[6] 李登峰.直覺模糊集決策與對策分析方法[M]．北京：國防工業出版社，2012．

[7] LI D F.Crucial and Unsolved Problems on Atanassov’s Intuitionistic Fuzzy Sets[J].Advances in Fuzzy Sets and Systems，2012，11（1）：57-64．

[8] HWANG C L，YOON K.Multiple Attributes Decision Making Methods and Applications[J].Springer Berlin Heidelberg，1981，164（4）：287-288．

[9] SAATY T L.The Analytic Hierarchy Process，Planning，Piority Set-ting，Resource Allocation[M].New York：Mc Graw-Hill，1980．

[10] WU D T，LI D F.Shortcomings of Analytical Hierarchy Process and the Path to Improve the Method （In Chinese） [J].Journal of Beijing Normal University：Natural Science，2004，40（2）：264-268.

[11] ZHANG Q，TAKASHI N.Some Methods of Raising Exactness of Evaluation in AHP（In Chinese）[J].Systems Engineering—Theory &Practice，1997，17（11）：29-35．

[責任編輯：彭壽康]

Credit Risk Evaluation of Small and Medium Enterprises Based on Intuitionistic Fuzzy Sets

ZHANG Xiao, WU Jian, CAO Qingwei
(School of Economics and Management, Zhejiang Normal University, Jinhua, 321004, China)

O159; F832.4

A

1671-4326 (2017) 03-0067-07

10.13669/j.cnki.33-1276/z.2017.059

2017-03-08

張 笑（1993—），女，江西鷹潭人，浙江師范大學經濟與管理學院碩士研究生；吳 堅（1977—），男，江蘇無錫人，浙江師范大學經濟與管理學院講師，博士；曹清瑋（1982—），女，江蘇無錫人，浙江師范大學經濟與管理學院講師，碩士．