聯系實際整體考慮

◎ 相 輝

聯系實際整體考慮

◎ 相 輝

有關圓的周長計算，題型多樣，方法不一，如果不聯系實際，不從整體出發，往往容易出錯且不易解答。例如：

聯系實際求周長

例1：一個鬧鐘的分針長5厘米，經過一晝夜，分針的針尖走過多少厘米？

【分析與解】

有的學生認為求分針針尖走過的厘米數就是求5厘米為半徑的圓的周長，即2×3.14×5=31.4（厘米）。其實分針一晝夜轉了2圈，不是圓一圈的周長，而是圓周長的2倍。所以分針走過的厘米數是2×3.14×5×2=62.8（厘米）。

例2：下圖是一個操場，直跑道100米，半圓直徑60米。請你求出繞著它跑一圈的距離。

【分析與解】

聯系生活實際，求圍操場跑一圈的距離，就是求2條相等長邊和兩個相同的半圓弧長的總和，不能加上兩條直徑。所以跑一圈的距離是100×2+3.14×60=388.4（米）。

整體考慮求周長

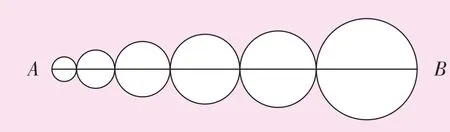
例3：已知AB=200分米，即下圖6個圓直徑的總和，求這6個圓周長的總和。

【分析與解】

6個圓的直徑沒有分別給出，也不易求出。我們可以從整體進行考慮，設這6個圓的直徑分別是 R1、R2、R3、R4、R5、R6，則這 6 個圓的周長分別為 πR1、πR2、πR3、πR4、πR5、πR6，周長總和就是C=πR1+πR2+πR3+πR4+πR5+πR6=π（R1+R2+R3+R4+R5+R6）

而R1+R2+R3+R4+R5+R6的和就是200分米，所以圖中6個圓周長的總和是3.14×200=628（分米）。

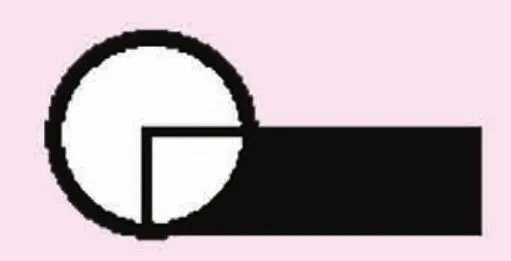
例4：把一個周長是12.56厘米的圓沿著半徑剪開，拼成如下的一個長方形，求圖中陰影部分的周長。

【分析與解】

陰影部分的周長是由三條線段和一段弧線組成的，如果逐個計算再求和，雖然可以，但比較麻煩。我們結合圓形轉化成長方形的過程，發現三條線段合起來就是圓的周長，圓弧是圓周長的，所以陰影部分的周長是12.56+12.56÷4=15.7（厘米）。