基于試驗結果的碰撞前車速誤差的校正?

張 健，梁 超，高金貴，丁同強，李 江

基于試驗結果的碰撞前車速誤差的校正?

張 健1，梁 超1，高金貴1，丁同強2，李 江2

(1.北華大學汽車與建筑工程學院，吉林 132013； 2.吉林大學交通學院，長春 130022)

為控制基于典型汽車碰撞模型計算的碰撞前車速誤差，采用了反推算法。對2起車輛碰撞事例進行了碰撞前車速的模擬和試驗。模擬結果表明，碰撞后車速誤差是影響模型計算的碰撞前車速準確性的關鍵因素，而相對而言力學參數誤差的影響則小得多。以碰撞試驗結果為準確值對模擬計算的碰撞前車速誤差進行了不同校正的研究。結果表明，對碰撞后車速誤差和力學參數誤差進行一次校正就能夠消除碰撞前車速誤差。研究結果證明該模型和算法具有極好的穩定性和收斂性。

碰撞前車速；碰撞后車速；誤差

Keywords:pre-crash speed； post-crash speed；error

前言

在汽車碰撞事故分析中，準確計算碰撞前車速至關重要。汽車碰撞事故分析有多種方法，其中基于動量守恒定律的典型汽車碰撞模型(以下簡稱模型)被廣泛用于計算碰撞前車速[1]。通常采用反推算法(以下簡稱反推法)計算碰撞前車速，即根據現場勘查數據，應用動能定理和運動學公式計算碰撞后車速，然后將其代入模型計算碰撞前車速[2-3]。實用中發現，應用動能定理和運動學公式計算的碰撞后車速有時不符合實際情況。因此，應用模型計算的碰撞前車速難免也存在誤差。盡管有些學者研究了模型中主要參數誤差對碰撞前車速的影響規律[4-5]，但是鑒于碰撞后車輛運動的復雜狀態，應用動能定理和運動學公式難以準確計算碰撞后車速。國外多利用已開發的事故分析軟件和配套的事故車輛與現場參數數據庫，通過模擬迭代的正推算法計算出與停車位置吻合的碰撞前車速[6-8]，并不斷對數據庫進行更新。目前國內進行的相關研究甚少，缺乏完整的事故車輛和現場參數數據庫，故多根據實際經驗對模型計算的碰撞前車速誤差進行調整[9]，這種方法速度慢且準確性難以保證。為對汽車碰撞事故做出準確的分析，剔除實用中模型存在的瑕疵，對碰撞前車速誤差進行校正的研究具有重要的意義。

1 模型

模型基于切向和法向坐標系建立。以車輛2(被撞車輛)的質心垂直被撞面向外為n軸(法向坐標軸)，n軸逆時針旋轉90°為τ軸(切向坐標軸)。為統一車速和車輛轉動角速度的方向，在車輛1和車輛2的質心上建立坐標軸方向相同的切向和法向坐標系，即τicini坐標系(下標i＝1，2表示車輛1和車輛2)。應用動量守恒定律和碰撞中心彈性變形條件，文獻[10]中建立的模型為

式中:A0和A分別為碰撞前車速系數矩陣和碰撞后車速系數矩陣；v0和v分別為碰撞前車速矩陣和碰撞后車速矩陣(以下簡稱碰撞前和碰撞后車速)。v0＝(v10n，v10τ，v20n，v20τ，ω10，ω20)T和 v＝ (v1n，v1τ，v2n，v2τ，ω1，ω2)T，其中:vi0n和 vi0τ分別為碰撞前車速的法向和切向分量；i＝1，2表示車輛 1和車輛 2；ωi0為碰撞前車輛的橫擺角速度(以下簡稱碰撞前角速度)；vin和viτ分別為碰撞后車速的法向和切向分量；ωi為碰撞后角速度。

式中:mi為車輛質量；ai和bi分別為碰撞中心的切向坐標和法向坐標(簡稱切向坐標和法向坐標)；Ji為車輛過質心繞垂向軸的轉動慣量；μ和k分別為碰撞中心切法比和彈性恢復系數(二者皆為力學參數)。 將 A0中第 6 行元素依次用 1，0，-1，0，-a1，a2替代后得到A。

2 算法與誤差

反推法就是先根據事故車輛損壞情況估算μ和k，再根據事故現場勘查數據計算碰撞后車速v，最后應用模型計算碰撞前車速v0的計算過程。應用動能定理公式和運動學公式計算的v和根據事故車輛損壞情況估算的μ和k難免存在誤差，而用車輛碰撞試驗結果檢驗反推法計算的碰撞前車速是研究誤差原因的有效方法。用于研究碰撞前車速誤差原因的2起車輛碰撞試驗現場分別如圖1和圖2所示。試驗數據[11-12]列于表1。

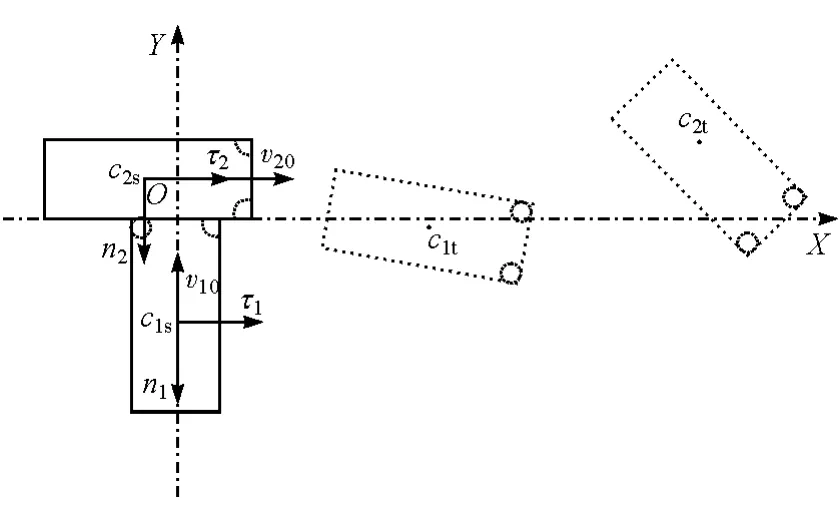
圖1 試驗I現場簡圖

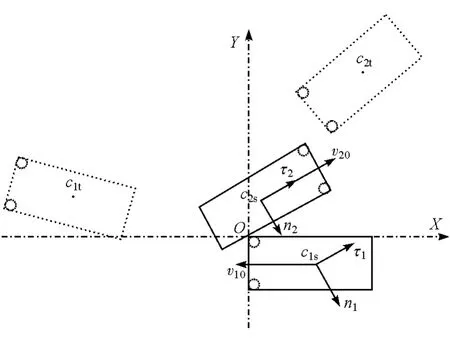
圖2 試驗II現場簡圖

表1 試驗數據

表1中:X和Y為車輛質心在地面坐標系(XOY坐標系)中的坐標值；θ為車輛縱軸與X軸正向的夾角(逆時針為正)；下標s為碰撞接觸瞬間的值；下標t為停車位置的值。

(1)計算碰撞后車速

根據試驗現場簡圖(圖1和圖2)，碰撞后車輛的滑行距離si和滑行方向角γi為

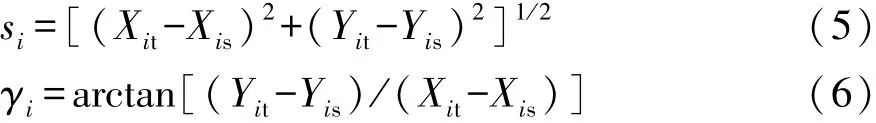
式中:si和γi為碰撞后車輛的滑行距離和滑行方向角(與X 軸逆時針的夾角為正)；(Xis，Yis)和(Xit，Yit)分別為碰撞接觸瞬間和停車位置車輛質心在XOY坐標系中的坐標值。

應用動量定理和運動學公式推導出的碰撞后車速計算公式為

式中:viX和viY為碰撞后車速的X軸和Y軸分量；g為重力加速度；fi為路面摩擦因數；ωi為碰撞后角速度；θit和θis為碰撞后停車位置車輛方向角和碰撞前車速方向角；(θit-θis)為車輛轉角。

以O點(碰撞中心)為原點的XOY坐標系和以車輛質心為原點的τcn坐標系之間可以進行坐標轉換[13]。轉換至τcn坐標系后的坐標值和車速值列于表2。

表2 轉換后的坐標值和車速值

根據表2，由式(3)和式(4)計算得到試驗I時μI＝1.301217039 和 kI＝-0.536883603。

(2)計算碰撞前車速

根據表 1、表 2，μI和 kI，由式(2)得到 A0和 A。將A0，A和表 2中碰撞后車速 v＝(-2.6235，6.3285，-0.5417，10.3709，-3.4936，-1.0371)T代入式(1)中，計算得到 v0＝(-3.8751，4.6999，0.6418，11.9109，-1.9719，-0.7694)T。 將 v0與表 2中試驗 I的結果 v0T＝(-4.94，0，0，14.39，0，0)T(準確值)進行對比，發現v0存在較大誤差。

3 誤差的原因和校正

根據反推法的計算過程，v，μ和k是導致v0存在誤差的因素。根據式(3)和式(4)，v和μ，k分別有6個和4個影響分量。為此，以試驗I為例，先以對 v 進行校正。 將 A0，A 和 v0T＝(-4.94，0，0，14.39，0，0)T代入式(1)中，計算得到 v＝(-3.6884，1.6286，-1.1835，12.85，-1.5217，-0.2677)T(校正)。將 v(校正)代入式(1)，計算得到 v0＝(-4.9399，0.0001，-0.0001，14.3899，0，0)T(校正)。計算結果表明:v的誤差是影響v0準確性的關鍵因素。

將 v0T＝(-4.94，0，0，14.39，0，0)T和 v(校正)代入式(3)和式(4)，計算得到μ＝1.3010279(校正)和 k＝-0.536869433(校正)。 根據表 1、表 2，μ(校正)和 k(校正)，由式(2)得到 A0(校正)和 A(校正)。

將A0(校正)，A(校正)和v(校正)代入式(1)，計算得到 v0＝ (-4.94，0.0003，0，-14.3897，-0.0002，-0.0001)T(校正)。結果表明:對μ和k校正后，碰撞前車速反而偏離準確值。因此，應分別對μ 或 k校正。 根據表1、表 2，μ(校正)和 kI，由式(2)得到A0(部分校正)和A(部分校正)。將A0(部分校正)，A(部分校正)和v(校正)代入式(1)，計算得到 v0＝ (-4.9399，0.0004，-0.0001，-14.3897，-0.0003，-0.0001)T(部分校正)。對μ或k進行3種校正后的計算結果列于表3。

由表3可知:力學參數誤差對碰撞前車速準確性的影響極小；而碰撞后車速誤差對碰撞前車速準確性的影響起決定性作用。

同理，以試驗II的結果為準確值進行反推法碰撞前車速誤差校正后的計算結果列于表4。

對比表3和表4可知:(1)試驗I對v進行校正后，碰撞前車速中誤差最大值僅為0.000 4(校正③)，可見力學參數誤差對碰撞前車速準確性的影響很小，因此，碰撞后車速誤差對碰撞前車速準確性的影響起決定性作用；(2)試驗II的校正①～校正④，碰撞前車速誤差更小，說明試驗II受力學參數誤差的影響更小；(3)在表3和表4中，校正④效果最好，表明在消除碰撞前車速誤差的過程中對k的誤差校正作用更明顯。

表3 誤差校正結果I

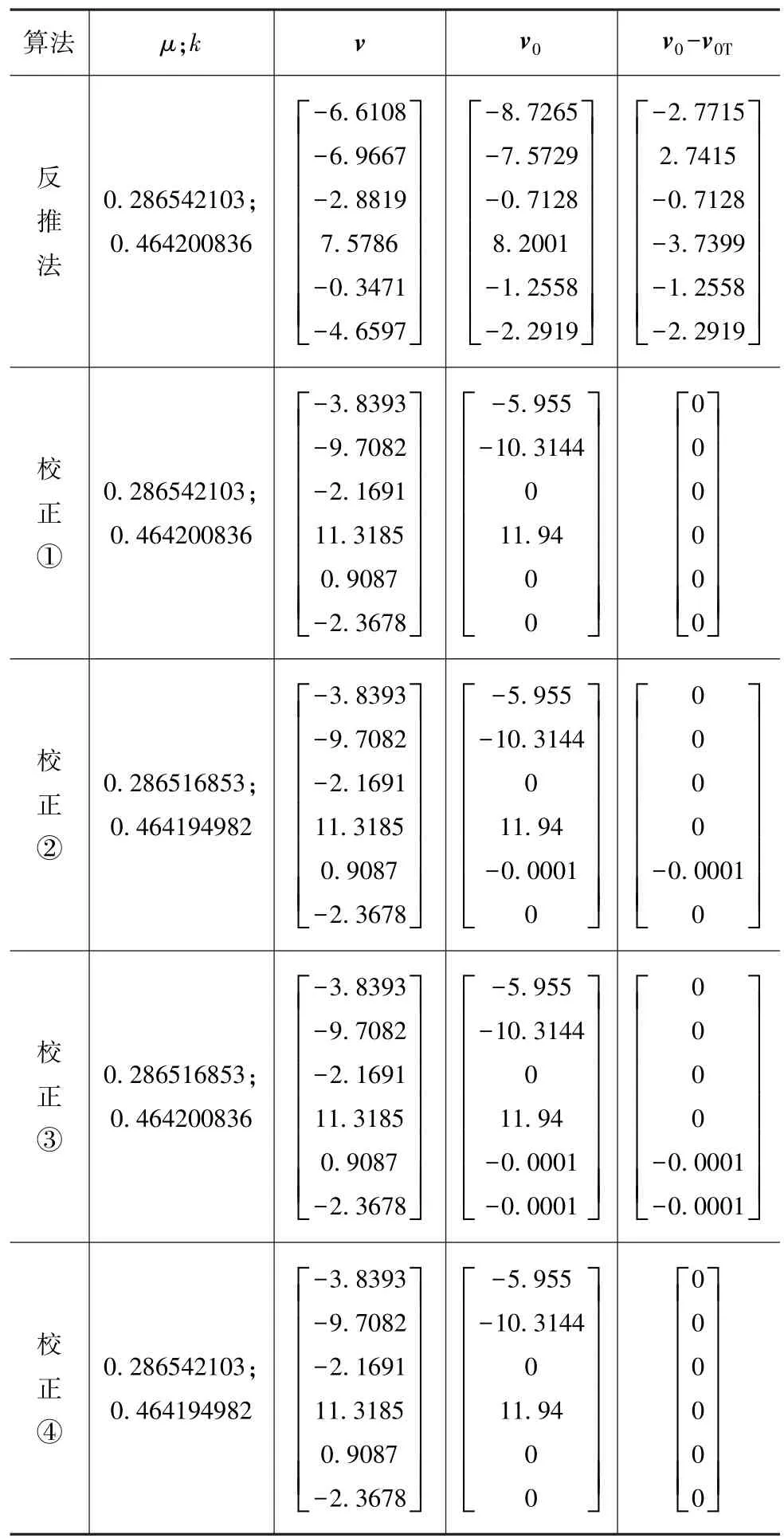
表4 誤差校正結果II

對比圖1和圖2，試驗I和試驗II在碰撞情況上的主要差別在于:碰撞位置與角度和碰撞前、后的車速不同。這些差別對力學參數產生直接的影響，為此，建立如下分析指標:式中:Eμ為碰撞中心切法比的相對誤差；μ為碰撞中心切法比的估算值；μA為碰撞中心切法比的校正值；Ek為彈性恢復系數的相對誤差；k為彈性恢復系數的估算值；kA為彈性恢復系數的校正值。

根據表5，對比分析指標Eμ和Ek，試驗I均大于試驗II。結果表明，試驗II受力學參數誤差的影響更小，因此，更易于徹底消除碰撞前車速誤差。

表5 力學參數影響分析指標

4 結論

以2起車輛碰撞試驗結果為準確值對模型反推法計算的碰撞前車速誤差進行了校正研究。結果表明:碰撞后車速誤差是導致碰撞前車速誤差的決定性原因，而相對而言力學參數誤差的影響則小得多。對碰撞試驗模擬計算的結果表明，只需對碰撞后車速誤差和力學參數誤差進行一次校正即可得到準確的計算結果，從而證明模型和算法具有極好的穩定性和收斂性。對車輛碰撞情況的研究表明力學參數相對誤差越小越易于徹底消除碰撞前車速誤差。研究成果提供了一種簡單有效的碰撞前車速誤差校正方法；確立了徹底消除碰撞前車速誤差的研究目標。

[1] 郝洪濤，余志遠，滕飛.基于VB的典型交通事故形態車輛行駛速度鑒定[J].農業裝備技術，2010，36(3):54-55.

[2] 張健，張鑫，李江，等.典型汽車碰撞模型自選參數的敏感性分析[J].汽車工程，2012，34(10):905-908.

[3] 劉志強，汪澎，張建華.斜碰撞再現反推算法研究[J].公路交通科技，2009，26(1):144-148.

[4] 張健，張鑫，梁超，等.車輛轉動慣量估算誤差對碰撞前車速估算值的影響[J].汽車工程，2015，37(2):175-178.

[5] 張健，張鑫.汽車碰撞模型中力學參數誤差對碰撞前車速的影響[J].西南交通大學學報，2011，46(2):259-263.

[6] NEADE J，SMITH R.The determination of vehicle speeds from delta-V in two vehicle planar collisions[J].Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering，2011，225(1):43-53.

[7] LIU Chunke， SONG Xinping， WANG Jiao.Simulation analysis of car front collision based on LS-DYNA and hyper works[J].Journal of Transportation Technologies，2014，4(4):337-342.

[8] PRENTKOVSKISO，SOKOLOVSKIJE，BARTULISV.Investigating traffic accident:a collision of two motor vehicles[J].Transport，2010，25(2):105-115.

[9] 李江，張大強，吳建平，等.事故再現中對速度計算結果的調整[J].公路交通科技，2003，20(2):104-107.

[10] 李江.交通事故力學[M].北京:機械工業出版社，2004.

[11] 魏朗，陳蔭三，石川，等.車輛碰撞過程的試驗分析研究[J].汽車工程，2000，22(4):256-261.

[12] 魏朗，郭應時，余強.車輛實車碰撞試驗的模擬再現[J].西安公路交通大學學報，2000，20(1):88-91.

[13] 張建.汽車碰撞事故模型病態性處理方法的研究[D].長春:吉林大學，2007.

Correction of Pre-crash Speed Error Based on Test Results

Zhang Jian1， Liang Chao1， Gao Jingui1， Ding Tongqiang2＆ Li Jiang2
1.College of Automible and Civil Engineering， Beihua University， Jilin 132013； 2.College of Transportation， Jilin University， Changchun 130022

To control pre-crash speed error calculated with typical vehicle collision model，reverse derivation algorithm is adopted，with test and simulation on pre-crash speed conducted.The results of simulation show that post-crash speed error is the key factor affecting pre-crash speed error，while the effects of mechanics parameters are relatively insignificant.With the crash test results taken as reference base，a study is performed on the different corrections on the errors of pre-crash speed simulated.The results show that pre-crash speed error can be eliminated by just one correction on post-impact speed error and mechanics parameter error，demonstrating the good stability and convergence property of the model built and the algorithm adopted.

10.19562/j.chinasae.qcgc.2017.09.008

?國家自然科學基金(51178001和31570556)和吉林市科技發展計劃項目(20090404)資助。

原稿收到日期為2016年6月3日。

張健，教授，E-mail:zhjdp＠126.com。