基于近似極小值原理的插電式混合動力汽車實時控制策略研究?

曾育平，秦大同

基于近似極小值原理的插電式混合動力汽車實時控制策略研究?

曾育平1，秦大同2

(1.南昌工程學院，江西省精密驅動與控制重點實驗室，南昌 330099； 2.重慶大學，機械傳動國家重點實驗室，重慶 400044)

將發動機的瞬時油耗擬合成由一次函數和二次函數組成的分段函數，將電池瞬時等效油耗擬合成由兩個二次函數組成的分段函數，在此基礎上，通過對Hamilton函數的分析，并根據凸函數的性質提出了通過縮小最優控制變量搜索空間來縮短尋優時間的近似極小值原理控制策略，然后選取一段隨機工況分別對此控制策略進行仿真和整車道路試驗，并分別對基于規則的CD-CS模式控制策略和基于近似極小值原理的控制策略進行整車對比道路試驗。仿真和整車道路試驗結果表明，本文中提出的基于近似極小值原理的控制策略實時性好，能應用于車輛實時能量管理控制，且具有良好的燃油經濟性，與基于規則的CD-CS模式控制策略相比，整車等效燃油消耗約降低23%。

插電式混合動力汽車；近似極小值原理；實時控制策略

Keywords:plug-in hybrid electric vehicle； approximate Pontryagin's minimum principle； real time control strategy

前言

整車控制策略是插電式混合動力汽車的關鍵技術之一，其對整車的燃油經濟性和排放性能具有重要影響，目前對插電式混合動力汽車整車能量管理控制策略的研究主要集中在以下兩個方面。

(1)基于等效燃油消耗最小的瞬時優化控制策略研究。文獻[1]和文獻[2]中研究了已知行駛工況下的等效燃油消耗最小插電式混合動力汽車控制策略；文獻[3]中研究了計及電池健康程度的等效燃油消耗最小的多目標瞬時優化控制策略；文獻[4]中研究了在未知行駛工況條件下等效系數自適應調節的等效燃油消耗最小控制策略。

(2)基于極小值原理或基于動態規劃等算法的全局控制策略研究。文獻[5]和文獻[6]中研究了已知行駛工況下的極小值原理控制策略；文獻[7]中通過模型預測控制在線調節拉格朗日因子從而實現了極小值原理在未知行駛工況下的應用；文獻[8]中研究了基于拉格朗日參數自適應調節的極小值原理控制策略；文獻[9]～文獻[11]中研究了基于動態規劃算法的插電式混合動力汽車控制策略。雖然這些控制策略的研究比較深入，但是這些控制策略的研究都是基于Matlab/Simulink的仿真研究，由于實時性差，很少應用于實際車輛。

本文中針對某單電機并聯式插電混合動力汽車，在擬合發動機的瞬時油耗和電池瞬時等效油耗的基礎上，通過分析Hamilton函數，并根據凸函數的性質提出了通過縮小最優控制變量搜索空間來縮短尋優時間的近似極小值原理控制策略。并通過Matlab/Simulink/Stateflow和D2P工具包Motohawk開發整車控制軟件，對該控制策略進行了實車道路試驗。

1 插電式混合動力汽車系統結構

本研究對象是單電機并聯式插電混合動力汽車，其動力系統結構如圖1所示，主要由發動機、ISG電機、濕式多片離合器C1、CVT(continuously variable transmission)、電動油泵、電池組和充電器組成。整車控制器通過控制濕式多片離合器的接合與分離實現整車工作模式的切換；通過控制電動油泵的運轉實現低轉速時蓄能器油壓與CVT油壓的建立；通過CAN總線實現與發動機控制器、電機控制器、電池管理系統、CVT控制器的通信，監測車輛的運行狀態，完成對ISG電機和發動機工作模式和轉矩、轉速的控制。插電式混合動力汽車動力系統參數見表1。

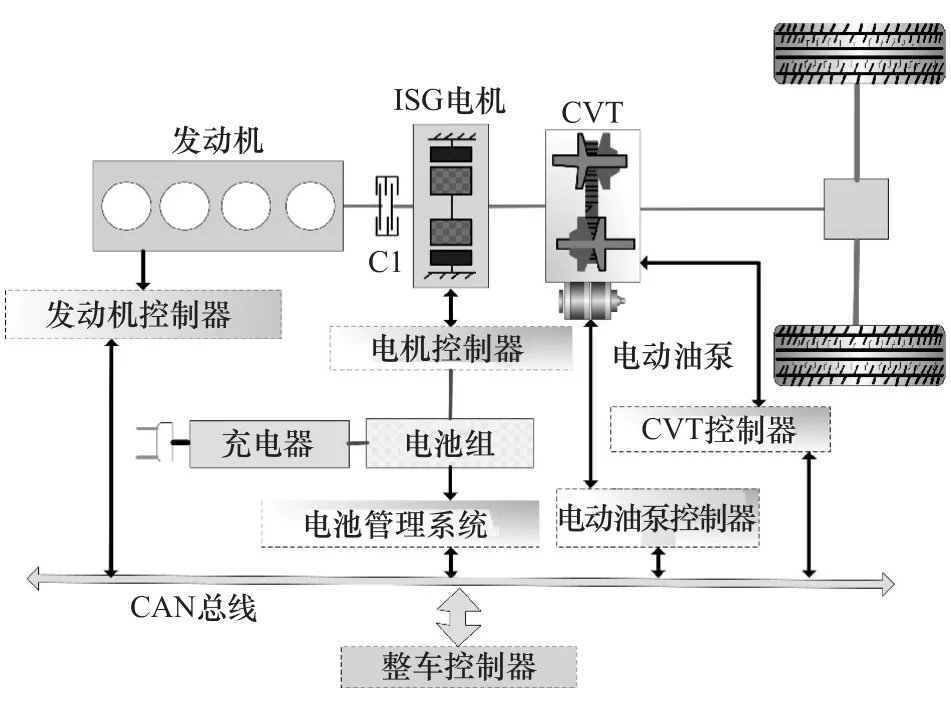
圖1 插電式混合動力汽車動力系統

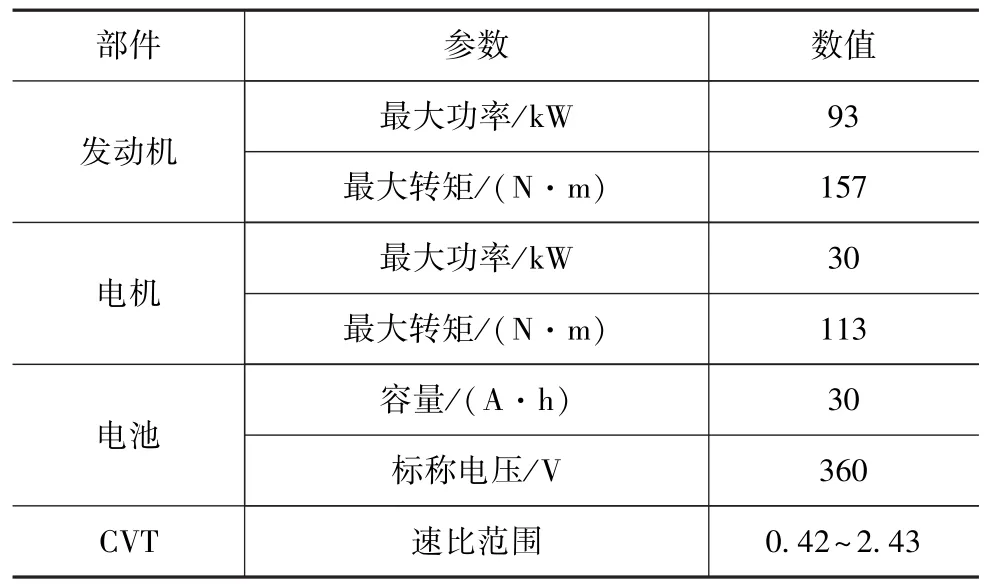
表1 插電式混合動力汽車的動力系統參數

2 基于近似極小值原理的控制策略

基于極小值原理的控制策略將全局優化轉化為瞬時優化，因此理論上該控制策略可以應用于實時控制，但是由于Hamilton函數是控制變量u(t)的復雜函數，并且在搜索最優控制變量時需要遍歷整個控制變量域，因此基于極小值原理的控制策略所需計算量大時間較長，實際上難以實現實時控制。為此本文中在擬合發動機瞬時油耗模型和電池瞬時等效油耗模型的基礎上，提出了通過縮小最優控制變量搜索空間來縮短尋優時間的近似極小值原理控制策略。

2.1 發動機瞬時油耗擬合模型

圖2為實測的發動機瞬時油耗曲線。圖中每條曲線上的星號對應于發動機該轉速下的燃油消耗率最低點。由圖可知，在一定的轉速下，發動機的瞬時油耗隨發動機輸出轉矩的變化關系可分為3段:第1段為發動機的瞬時油耗隨發動機輸出轉矩增大而迅速增大，其主要原因是發動機在此階段處于低負荷區，發動機的節氣門開度比較小，發動機燃燒室油/氣比濃度高，燃油燃燒速度比較慢；第2段為發動機的瞬時油耗隨發動機輸出轉矩的增加而線性增加，其主要原因是發動機在此階段處于中負荷區，發動機燃燒室油/氣比濃度較適中，發動機的輸出轉矩、輸出功率和瞬時油耗都隨節氣門的開度增大而近似線性增加；第3段為發動機的瞬時油耗隨發動機輸出轉矩增加而迅速增加，其主要原因是在此階段發動機處于高負荷區，發動機節氣門處于全開狀態，發動機輸出轉矩只能通過供油的增加而增加。對于插電式混合動力汽車，其發動機的實際工作要求是避免其工作在低負荷區，即避免工作在第1階段。

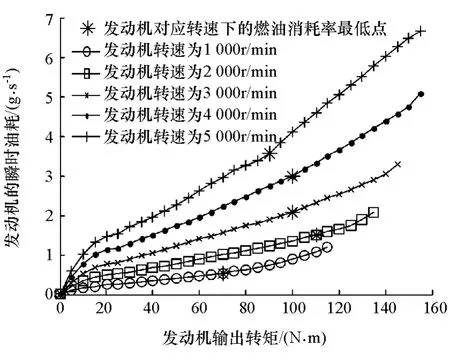
圖2 實測的發動機瞬時油耗曲線

通過對實測發動機瞬時油耗曲線的分析并結合插電式混合動力汽車發動機的實際工作要求，發動機的瞬時油耗曲線可以分別用線性函數和二次函數擬合，其擬合結果如圖3所示，星號左邊的實線通過線性擬合獲得，星號右邊的實線通過二次函數擬合獲得。圖中虛線為各轉速下發動機實測瞬時油耗曲線。由圖3可知，擬合值和實測值基本一致。因此發動機的瞬時油耗可表示為式(1)。根據凸函數的定義可以判定:在一定轉速下，發動機的瞬時油耗為[Temin，Temax]上的凸函數。

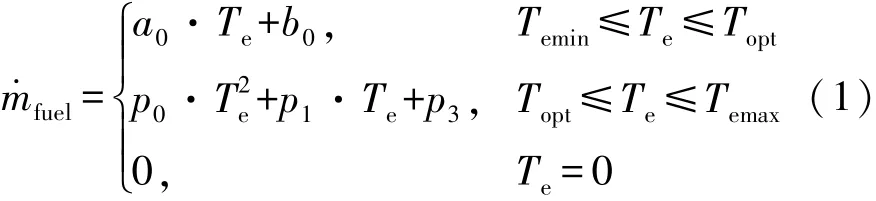
式中:a0，b0，p0，p1和 p3為擬合參數；Topt為各轉速下發動機燃油消耗率最低點所對應的轉矩；Temin和Temax分別為發動機在各轉速下的最小和最大轉矩。

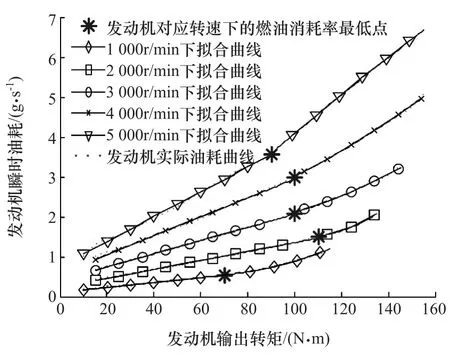
圖3 發動機瞬時油耗的擬合圖

2.2 電池瞬時等效油耗擬合模型

將電池瞬時能耗的變化等效為發動機瞬時能耗的變化，假設它們之間的轉換因子為s，則電池瞬時等效油耗可表示為

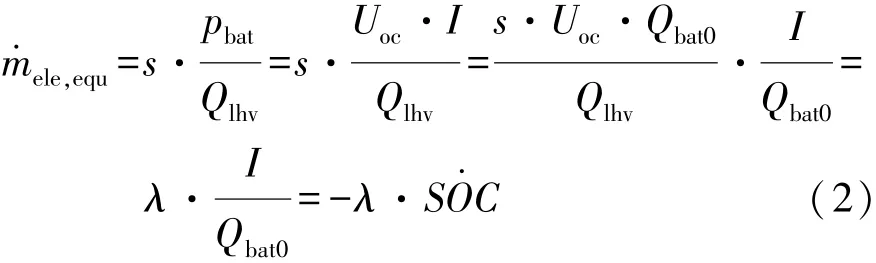
式中:pbat為電池充放電功率，W；Qlhv為燃油的低熱值，J/g；Uoc為電池電動勢；Qbat0為電池的額定容量；λ稱為等效系數。由式(2)可知，在已知行駛工況和一定的電池SOC下，電池瞬時等效油耗是電池SOC導數的線性函數，因此電池瞬時等效油耗的擬合模型可在電池SOC導數擬合模型的基礎上獲得。

根據電池內阻簡化模型，可計算SOC的導數:

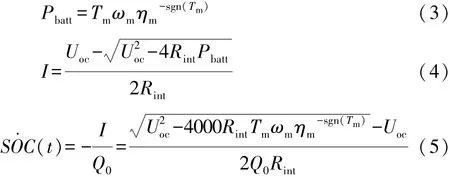
式中:Tm為電機輸出矩，N·m；ωm為電機的角速度，rad/s；Pm為電機功率，W；ηm為電機效率；I為電池電流，A；Pbatt為電池的充放電功率，W；Q0為電池的初始電量；Rint為電池內阻，Ω；Uoc為電池的開路電壓，V。

根據式(3)～式(5)算得的電池SOC導數精確值擬合出曲線，圖4為電池SOC為0.5時的SOC導數擬合曲線，其中小圓點為計算的數據點，每條曲線都由兩個二次函數擬合組成，電機輸出轉矩為0的點為兩段二次曲線的連接點。因此電池SOC的導數可表示為

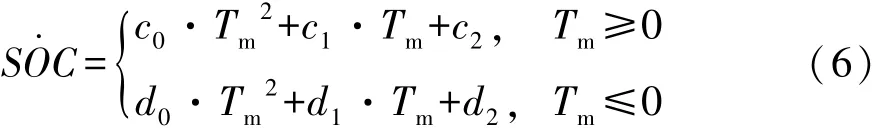
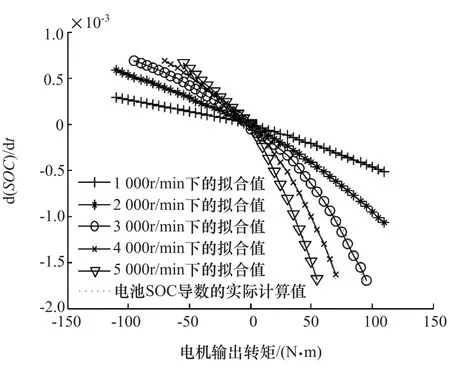
圖4 電池SOC為0.5時的SOC導數擬合曲線

圖5 為電池SOC為0.5且λ為1 800時的電池瞬時等效油耗曲線。由圖5和凸函數的定義可知，在一定的轉速下，電池瞬時等效油耗為[Tmmin，Tmmax]上的凸函數，Tmmin和Tmmax分別為電機在該轉速下的最小和最大轉矩。

圖5 電池SOC為0.5時的電池等效油耗曲線

2.3 Hamilton函數

目標函數取得最小值的條件是Hamilton函數在控制變量的容許可達集內取得極小值。式(7)為Hamilton函數，是由發動機瞬時油耗和電池瞬時等效油耗組成的總等效油耗。

由于發動機瞬時油耗和電池瞬時等效油耗分別是 Te∈[Temin，Temax]和 Tm∈[Tmmin，Tmmax]上的凸函數，且二者的中間轉折點分別為Te＝Topt和 Tm＝0。由凸函數的性質可知，Hamilton函數為Tm∈[Umin，Umax]上的凸函數，Umin和 Umax為

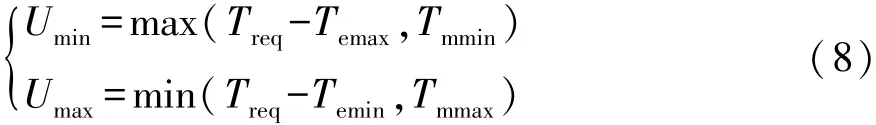
式中:Treq為發動機和電機的總需求轉矩，因此Hamilton函數在Tm∈[Umin，Umax]上的極小值只可能在Tm＝Umin，Tm＝Treq-Topt，Tm＝0 和 Tm＝Umax4 個點取得。 當 Te＝0，即 Tm＝Treq時，Tm?[Umin，Umax]，因此Hamilton函數在Tm＝Treq處也可能取極小值。綜上所述，Hamilton函數的極小值，即目標函數的最小值只可能從以下 5個點取得:Tm＝Umin，Tm＝Treq-Topt，Tm＝0，Tm＝Umax和 Tm＝Treq，因此只需比較這 5 個點的Hamilton函數值的大小就可以確定最優解。這就將最優解的搜索區域由整個控制變量的容許可達集簡化到了5個搜索點，大大減少了計算時間和計算存儲空間。

3 結果與分析

3.1 基于近似極小值原理控制策略的仿真結果與整車道路試驗結果對比分析

為驗證本文中提出的控制策略的實時性和控制效果，在同一隨機工況下對此控制策略分別進行了仿真和整車道路試驗，仿真在臺式電腦上進行，該電腦具有8GB內存、四核主頻3.1GHz處理器和64位Win7操作系統。試驗采用的控制器為D2P，其內存為64KB，處理器為 80MHz主頻的 Motorola MPC5554。控制策略的仿真軟件在Matlab/Simulink平臺上開發，整車實車控制軟件在Matlab/Simulink/Stateflow和D2P工具包Motohawk平臺上開發，圖6為等效系數λ＝1800時的整車仿真結果和道路試驗結果對比圖。

圖6(a)為選取的隨機工況，包括需求轉矩和車速隨時間的變化曲線。由需求轉矩曲線可知，整個過程中包括了起動、加速、急加速和減速等階段。圖6(b)對比了在此隨機工況下發動機輸出轉矩的仿真值和道路試驗值。圖6(c)對比了在隨機工況下電機輸出轉矩的仿真值和道路試驗值。由圖6(b)和圖6(c)可見，除了在發動機起動和關閉過程外，發動機和電機輸出轉矩的仿真值和試驗值基本一致，在發動機起動和關閉過程中，發動機輸出轉矩的試驗值要稍微滯后發動機輸出轉矩的仿真值，這是因為仿真過程中未考慮模式切換，而實車的控制軟件考慮了模式切換，試驗結果中的發動機輸出轉矩相對于仿真結果中的發動機輸出轉矩的滯后時間即為模式切換時間。在圖6(c)中，在發動機起動過程中，試驗結果中的電機輸出轉矩會出現一個峰值，而仿真結果中沒有，這是因為由純電動切換到純發動機驅動的模式切換過程中，電機需要提供比較大的補償轉矩。總的來說，整車道路試驗結果與仿真結果基本吻合，說明本文中提出的控制策略實時性好，可應用于實車的能量管理控制。

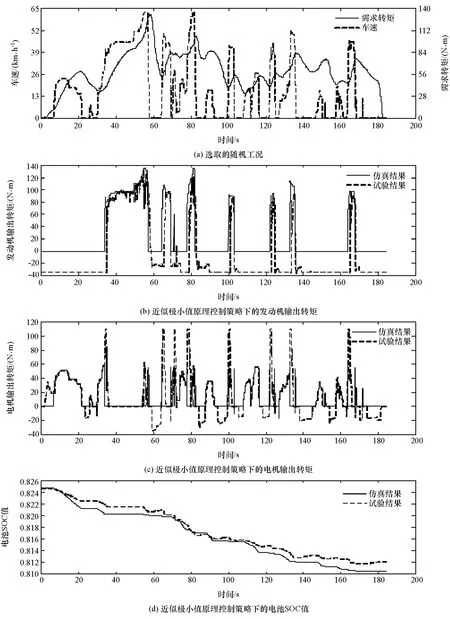
圖6 近似極小值原理的仿真結果與試驗結果對比圖

圖7 為整車仿真結果與道路試驗結果中發動機工作點對比圖。由圖可見，仿真結果中的發動機工作點和試驗結果中發動機工作點基本處于同一區域，且該區域總體為經濟工作區，表明本文中提出的控制策略能合理地分配發動機和電機轉矩。

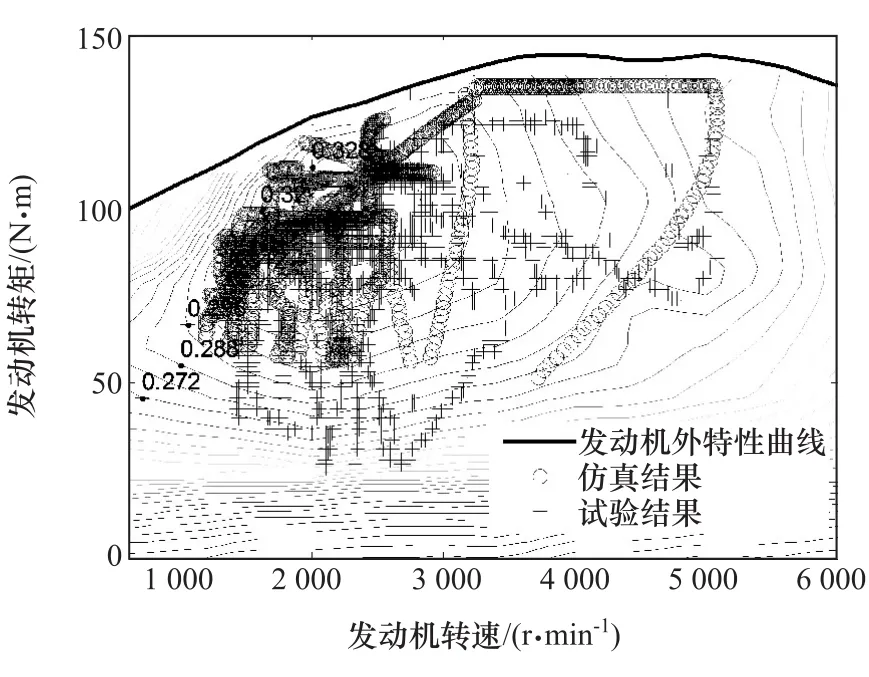
圖7 發動機工作點

3.2 基于規則CD-CS模式控制策略和基于近似極小值原理控制策略的整車對比道路試驗結果分析

根據國標GB/T 19753—2013《輕型混合動力電動汽車能量消耗量試驗方法》，整車的燃油經濟性通常是在底盤測功機上進行多個循環行駛工況測試來評價，但由于試驗條件限制，本文中用實際道路試驗來代替國標中的底盤測功機模擬試驗。

為便于對比，同時開發了基于規則的CD-CS模式控制策略的整車控制軟件，在此基礎上，按照相同的試驗要求和步驟對兩種控制策略進行對比試驗。

試驗前，車輛在20～30℃的溫度條件下的室內放置，直到發動機的潤滑油和冷卻液溫度與室溫之差在±2℃范圍內。車輛在室內放置期間，使用車載充電器對電池組進行充電，直至電池組完全充滿，然后在校園內選擇一個路段進行道路試驗，用車載油耗儀記錄發動機的油耗，試驗結果如表2所示。由表可見，與基于規則的CD-CS模式控制策略相比，基于近似極小值原理控制策略的整車燃油消耗降低了22.98%，表明基于近似極小值原理控制策略具有較好的燃油經濟性。

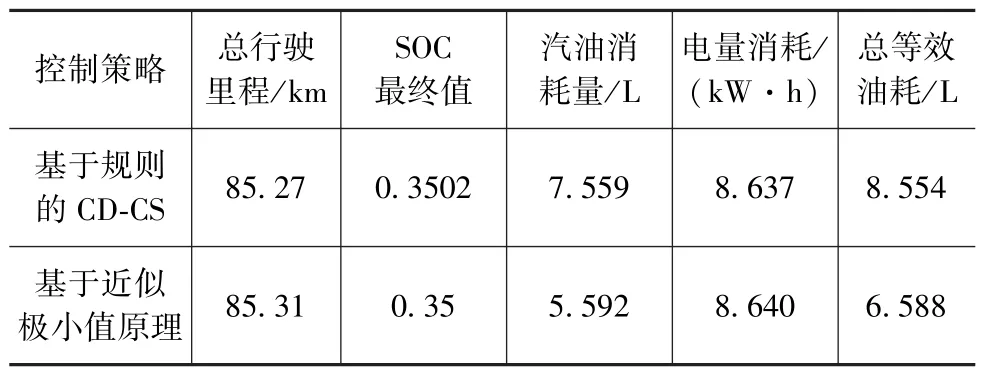
表2 兩種控制策略下的道路試驗結果

3.3 不同等效系數下的整車道路試驗結果分析

圖8為在同一路況下等效系數λ分別為1 200，1 800和2 000時的轉矩分配和電池SOC變化曲線。初始SOC為0.9，設定基于近似極小值原理控制策略下的SOC最低值為0.82，SOC低于0.82進入CS模式，即電量維持模式。由圖8可見，a1，b1和c1為整車工作在近似極小值原理控制策略模式，而a2，b2和c2為整車工作在CS模式。隨著等效系數λ的增加，發動機參與工作的比例增加，整車工作在近似極小值原理控制策略模式下的行駛里程增加。由圖8(d)可知，在λ＝1200，λ＝1800和λ＝2000時，整車工作在近似極小值原理控制策略模式下的行駛里程分別為 Sa＝4.78km，Sb＝8.18km 和 Sc＝13.53km。因此，等效系數λ需根據電池SOC值、行駛里程和路況參數進行在線調整。

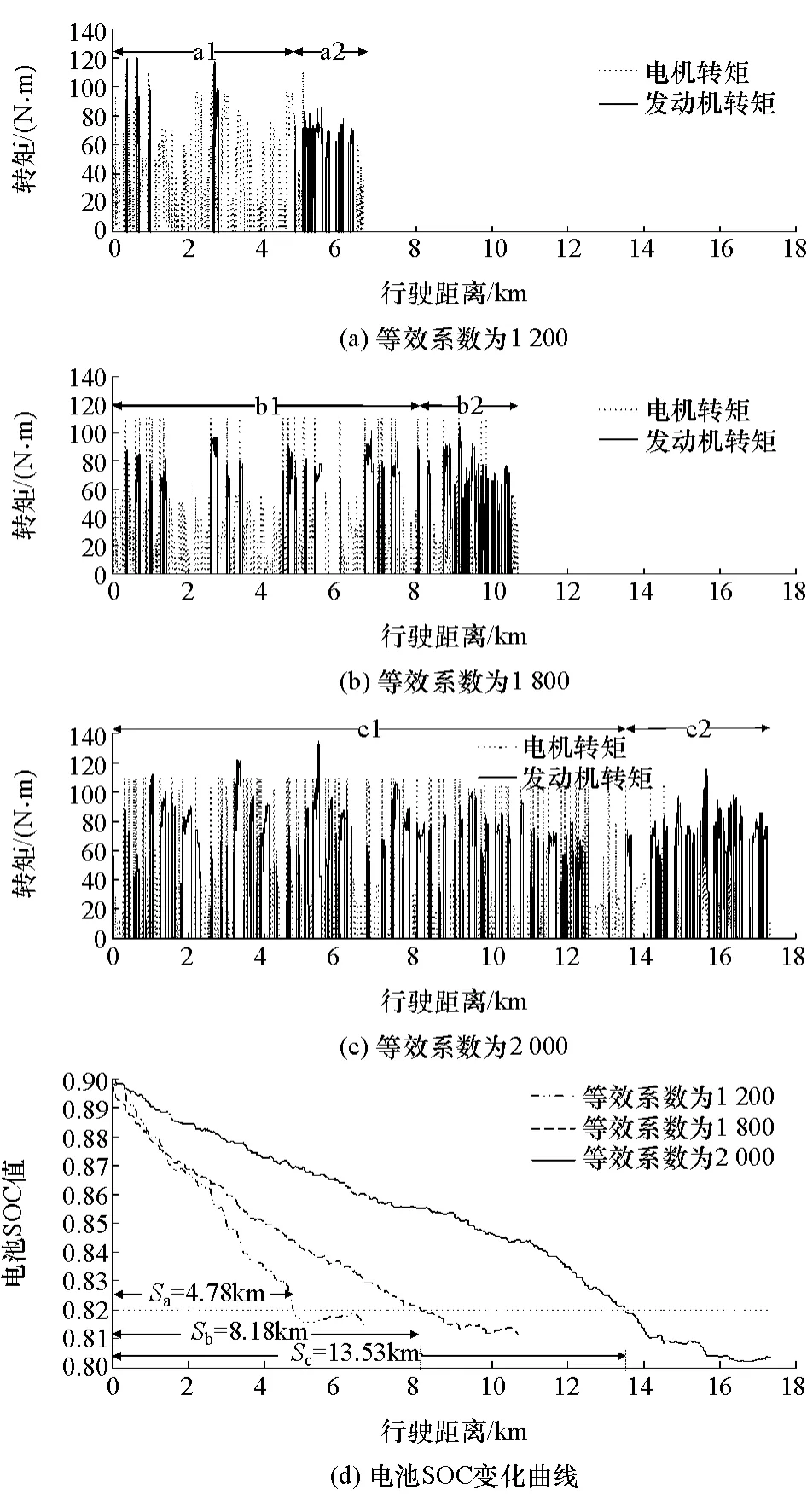
圖8 在不同等效系數下的轉矩分配及電池SOC曲線

4 結論

(1)本文中在獲得發動機瞬時油耗和電池瞬時等效油耗模型的基礎上，通過分析Hamilton函數，提出了基于近似極小值原理的插電式混合動力汽車控制策略，該策略將最優解的搜索區域由整個控制變量的容許可達集簡化到5個搜索點，大大縮短了計算時間并減小了計算存儲空間。

(2)在同一隨機工況下，對本文中提出的控制策略分別進行了仿真和整車道路試驗，仿真結果與道路試驗結果能很好吻合，且發動機工作點基本都分布在其經濟工作區，說明本文中提出的控制策略實時性好，能應用于實車能量管理控制，并能合理分配發動機和電機轉矩。

(3)進行了基于規則CD-CS模式控制策略和基于近似極小值原理控制策略的整車對比道路試驗，結果表明，與基于規則的CD-CS模式控制策略相比，基于近似極小值原理控制策略的整車燃油消耗降低了26.02%，表明基于近似極小值原理的控制策略具有較好的燃油經濟性。

(4)道路試驗還測試了整車在不同等效系數λ下的轉矩分配情況，結果表明隨著等效系數λ的增加，發動機參與工作比例增加，整車在近似極小值原理控制策略模式下的行駛里程增加。

[1] TULPULE P，MARANO V，RIZZONI G.Energy management for plug-in hybrid electric vehicles using equivalent consumption minimisation strategy[J].International Journal of Electric and Hybrid Vehicles，2010，2(4):329-350.

[2] ZHANG C，VAHID A.Real-time optimal control of plug-in hybrid vehicles with trip preview[C].American Control Conference(ACC)，2010.IEEE，2010:6917-6922.

[3] GENG B，MILLSJK，SUN D.Two-stage energy management control of fuel cell plug-in hybrid electric vehicles considering fuel cell longevity[J].IEEE Transactions on Vehicular Technology，2012，61(2):498-508.

[4] HE Y M，CHOWDHURY M，PISU P，et al.An energy optimization strategy for power-split drivetrain plug-in hybrid electric vehicles[J].Transportation Research Part C:Emerging Technologies，2012，22:29-41.

[5] KIM N，ROUSSEAU A，LEE D.A jump condition of PMP-based control for PHEVs[J].Journal of Power Sources， 2011， 196:10380-10386.

[6] STOCKAR S，MARANO V，CANOVA M，et al.Energy-optimal control of plug-in hybrid electric vehicles for real-world driving cycles[J].Vehicular Technology， IEEE Transactions on，2011，60(7):2949-2962.

[7] ZHENG C，XU G，ZHOU Y.Realization of PMP-based power management strategy for hybrid vehicles based on MPC scheme[C].Information Science and Technology(ICIST)，2014 4th IEEE International Conference on.IEEE，2014:682-685.

[8] ONORI S，TRIBIOLI L.Adaptive pontryagin's minimum principle supervisory controller design for the plug-in hybrid GM chevrolet volt[J].Applied Energy，2015，147:224-234.

[9] GONG Q，LI Y，PENG Z R.Trip-based optimal power management of plug-in hybrid electric vehicles[J].Vehicular Technology，IEEE Transactions on，2008，57(6):3393-3401.

[10] MOURA SJ，FATHY H K，CALLAWAY D S，et al.A stochastic optimal control approach for power management in plug-in hybrid electric vehicles[J].Control Systems Technology，IEEE Transactions on，2011，19(3):545-555.

[11] SHAMS-ZAHRAEI M，KOUZANI A Z，KUTTER S，et al.Integrated thermal and energy management of plug-in hybrid electric vehicles[J].Journal of Power Sources，2012，216:237-248.

A Study on Real-time Control Strategy for a Plug-in Hybrid Electric Vehicle Based on Approximate Pontryagin's Minimum Principle

Zeng Yuping1＆Qin Datong2

1.Nanchang Institute of Technology， The Jiangxi Province Key Labruary of Persision Drive and Contorl， Nanchang 330099；2.Chongqing University， The State Key Laboratory of Mechanical Transmission， Chongqing 400044

The instantaneous fuel consumption of engine is fitted with a piecewise function consisting of a linear function and a quadratic function，while the instantaneous equivalent fuel consumption of battery is fitted with a piecewise function consisting of two quadratic functions.On this basis， through the analysis of Hamilton function，and according to the properties of convex function，a control strategy based on approximate minimum principle is proposed，which shortens the optimization time by reducing the search space of optimal control variables.Then both simulation and vehicle road test are conducted on the control strategy with a chosen section of random driving condition，and a vehicle test to compare rule-based CD-CS mode control strategy and the control strategy based on approximate minimum principle is performed.The results of simulation and vehicle road test show that the control strategy based on approximate minimum principle has a better real-time performance and can be applied to the real time energy management control of vehicle with also a better fuel economy:its equivalent fuel consumption is around 23%lower than that with rule-based CD-CSmode control strategy.

10.19562/j.chinasae.qcgc.2017.09.005

?國家自然科學基金(51665020)、重慶大學機械傳動國家重點實驗室2016年開放基金(SKLMT-KFKT-201617)和江西省教育廳科學技術項目(GJJ161123)資助。

原稿收到日期為2015年4月20日，修改稿收到日期為2016年12月18日。

曾育平，博士，E-mail:zengyp198410＠163.com。