p-Laplacian橢圓型方程解的不存在性問題研究
朱勝蘭,李濤會
(無錫城市職業(yè)技術學院 無錫環(huán)境科學與工程研究中心, 江蘇 無錫 214153)
p-Laplacian橢圓型方程解的不存在性問題研究
朱勝蘭,李濤會
(無錫城市職業(yè)技術學院 無錫環(huán)境科學與工程研究中心, 江蘇 無錫 214153)
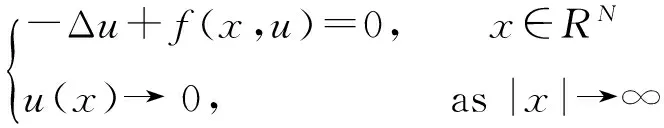
p-Laplacian橢圓型方程;Pohozaev恒等式;解的不存在性
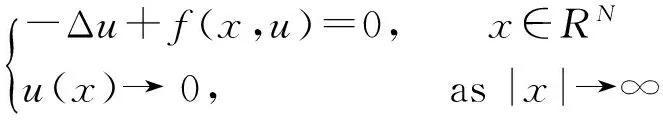
Keywords: p-Laplacian elliptic equations; Pohozaev constant equation; nonexistence of solutions
利用Pohozaev恒等式來證明偏微分方程沒有非平凡解始于1965年Pohozaev在文獻[1]中關于二階半線性橢圓型方程齊次Dirichlet問題的正則解建立的積分恒等式。由于Pohozaev恒等式在研究解的不存在性的同時也就得到了解存在的必要條件,從而引起了國內(nèi)外學者的重視,并被積極地推廣。
本文我們主要討論下面的p-Laplacian橢圓型問題
(1)
不存在非平凡解。
關于問題(1)解的存在性和非存在性及其多解性的研究已經(jīng)取得了豐富的成果。
2008年, Lari在文獻[2]中又研究了問題(1)在f(x,u)=p(x)uα+q(x)uβ時,即
Δu=p(x)uα+q(x)uβ
(2)
整體解的存在性和不存在性。這里0<α≤β,p,q是非負連續(xù)函數(shù)。筆者通過研究得到如下結(jié)果:
1) 假設0<α≤1<β且函數(shù)p,q滿足條件

(3)

2) 若方程Δv=q(x)vβ(β>1)沒有非負整體大解,那么半線性橢圓方程(2)也沒有非負整體大解。
另外,在文中 Lari還證明了方程
Δu=u+e-|x|uβ(β>2)
(4)
也沒有正的整體大解。
最近, Wu在文獻[3]中對式(1)中的

(5)
解的存在性問題進行了探索,筆者通過變分方法發(fā)現(xiàn)其在滿足一定條件時在RN上存在多個正解。這里1 與上面文獻不同的是:本文主要是利用Pohozaev恒等式來證明幾類p=2的p-Laplacian橢圓型方程解的不存在性。 (6) (7) (8) 注意到 (9) (10) 那么對于等式(8)有 (11) (12) 注意到 (13) 所以 (14) (15) 即存在rn→∞使得 (16) 下面用反正法來證明結(jié)論式(15)。 (17) 那么就可以取rn=r0+n,n=1,2,3,…,當所有n→∞時,rn→∞且r0 (18) 所以有 (19) 在式(14)中取r→∞得 (20) 結(jié)論得證,到此,定理1的證明全部結(jié)束。 定理2 假設定理1中的條件滿足,且f(x,u)∈L1(R1),若存在α∈R1,u≠0,使得 (21) 則方程 -Δu+f(x,u)=0x∈R (22) 沒有非平凡解。 下面用一個具體的例子進行說明。 例如:在全空間上考慮方程 (23) 這里,1 證明:由式(23)知此時式(6)中 所以 (24) (25) 則可以得到 (26) 所以 (27) 從而可得 (28) 那么根據(jù)所給的條件,方程(23)在下列3種情況下于空間εr,s內(nèi)均無平凡解: 1)r<2*,s<2*,λ1,λ2≥0; 2)r>2*,s>2*,λ1,λ2≥0; 3)r<2*,s>2*,λ1,λ2≤0。 本文首先介紹了由Pohozaev 提出的恒等式,然后運用它證明相關的p-Laplacian橢圓型方程解的不存在性,得到更廣泛的解存在的必要條件,并給出了一些具體的實例來驗證結(jié)論。 [1] POHOZAEV S.Eigenfunctions of the equation Δu+λf(u)=0[J].Soviet Math Dokl,1965(6):1408-1411. [2] LAIR A V.Large solutions of mixed sublinear-superlinear elliptic equations[J].Math Anal Appl,2008,346:99-106. [3] WU T F.Multiple positive solutions for a class of concave-convex elliptic problems in RN involving sign-changing weight[J].Funct.Anal.,2010,258:99-131. [4] MOSCHINI L,POHOZAEV S I,TESEI A.Existence and nonexistence of solutions of nonlinear Dirichlet problems with first order terms[J].Journal of Functional Analysis,2000,177:365-382. [5] OTANI M.Existence and nonexistence of nontrivial solution of some nonlinear degenerate elliptic equations[ J].Funct Anal,1988,76:140-159. [6] STRUWE M.Variational Methods[M].Berlin:Springer-Verlag,1996. [7] WAGNER A.Pohozaev identity from variational viewpoint[J].Math.Anal.Appl.,2002,266:149-159. [8] AN T Q.Non-existence of positive solutions of some elliptic equations in positive-type domains[J].Applied Mathematics Letters,2007,20:681-685. [9] DE PAIVA F O.Nonnegative solutions of elliptic problems with sublinear indefinite nonlinearity[J].Journal of Functional Analysis,2011,261:2569-2586. [10] 朱勝蘭.P-Laplacian 橢圓型方程的整體解[J].重慶理工大學學報(自然科學),2013,27(4):138-142. [11] LARI A V,WOOD A W.Large solutions of sublinear elliptic equations[J].Nonlinear Anal,2000,39:745-753. [12] LARI A V,WOOD A W.Existence of entire large positive solutions of semilinear elliptic systems[J].Diff.Equat,2000,164:380-394. (責任編輯何杰玲) StudyontheNonexistenceofSolutionsforP-LaplacianEllipticEquation ZHU Shenglan, LI Taohui (Wuxi Environmental Science and Engineering Research Center, Wuxi City College of Vocational Technology, Wuxi 214153, China) 2016-12-14 國家自然科學基金資助項目(11201115); 江蘇省科技廳基礎研究計劃(自然科學基金)——青年基金項目(BK20140126) 朱勝蘭(1984—),女,博士,講師,主要從事偏微分方程研究,E-mail:zhushenglan2164@126.com。 朱勝蘭,李濤會.p-Laplacian橢圓型方程解的不存在性問題研究[J].重慶理工大學學報(自然科學),2017(9):200-204. formatZHU Shenglan, LI Taohui.Study on the Nonexistence of Solutions for P-Laplacian Elliptic Equation[J].Journal of Chongqing University of Technology(Natural Science),2017(9):200-204. 10.3969/j.issn.1674-8425(z).2017.09.031 O29 A 1674-8425(2017)09-0200-051 主要結(jié)論







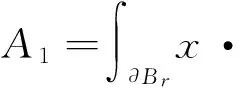




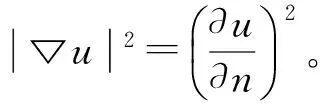




2 實例認證








3 結(jié)束語

