基于方差縮減的高維美式期權 Monte Carlo 模擬定價

陳金飚， 林榮斐

(臺州學院 數學與信息工程學院， 浙江 臺州 317000)

基于方差縮減的高維美式期權 Monte Carlo 模擬定價

陳金飚， 林榮斐*

(臺州學院 數學與信息工程學院， 浙江 臺州 317000)

美式期權給予持有者在到期日之前任何時刻的權利，因涉及最佳執行時刻問題定價較為復雜. Monte Carlo方法其估計誤差及收斂速度與問題的維數獨立，可較好地處理高維衍生證券問題，且方法靈活易于實現.利用最小二乘蒙特卡洛方法(LSM)，結合存儲量減小技術與方差縮減技術，將 Monte Carlo 模擬方法應用于多標的資產的美式期權定價，并比較、分析了不同方差縮減技術的效果及適用范圍.

Monte Carlo 方法；美式期權；方差縮減技術；定價

0 引 言

近年來隨著數據分析和計算機技術的飛速發展，高維美式期權的定價方法取得了實質性的突破[1-8]，但隨著美式期權維數的增加,存在所謂的“維數災難”問題.為了克服這一難題,研究者將Monte Carlo模擬美式期權定價作為重要的研究主題[9-10].

假設d維無紅利標的資產x=(x1,x2，…，xd)滿足幾何布朗運動

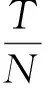
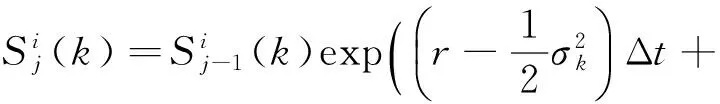
(1)

為d個獨立同分布的標準正態變量所組成的向量.

本文研究的美式看跌期權的收益均由標的資產價格的最大值決定，即期權收益為

(2)

BOYLE等[11]對美式期權的Monte Carlo模擬方法做了詳細介紹和綜述，其中提到：每生成一列Sti(i=0，1，…，N)的路徑后，一個明顯的估計量為

LONGSTAFF等[14]利用最小二乘法確定了一個“期望函數”，并以期望函數的值作為期權繼續持有的價值，與立刻執行的價值進行比較，決定是否提前執行.LSM方法的具體過程為：首先對每條模擬路徑，求出tN時刻的期權收益，作為相應路徑在tN時刻的期權收益貼現到tN-1時刻的現金流Y關于tN-1時刻d個標的資產的價格向量X的線性回歸，用最小二乘法求出回歸系數，稱所得的函數為條件期望函數.對期權收益為正的路徑，將tN-1時刻的X值代入線性回歸函數，求得相應的條件期望函數值.然后比較此值與在tN-1時刻執行的收益大小，以確定期權在該路徑上是否提前執行，進而計算tN-1時刻期權的價格.最后重復上述過程，依次計算前面各時刻美式期權的價格，直到t1時刻，計算所有路徑期權價格的平均值，取該平均值與0時刻期權價值中較大者作為期權價格的最終估計值.需要強調的是，在作線性回歸時， LSM方法僅對處于在值狀態(期權收益為正)的路徑進行回歸，其余路徑僅作為貼現，從而減少了計算時間，大大提高了算法的效率.

1≤i≤M，

(3)

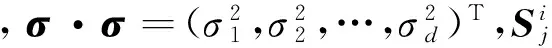
(4)

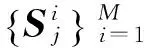
1 基于方差縮減的LSM算法

1.1 方差縮減優化方法

文獻[10-11]詳細介紹了各種方差縮減技術的理論依據，并用數值例子進行了比較和分析.本文選用了其中2種方法：對偶變量法和控制變量法.用數值例子比較這2種方法在處理實際問題時的效果.

1.1.1 對偶變量法

下面討論對偶變量法的方差縮減效果和運算效率.從理論上說，因為估計量Y1和Y2的方差相同，所以

(5)

如果Cov[Y1,Y2]≤Var(Y1)，那么就有Var(YAV)≤Var(Y1).但是YAV的計算量是Y1的2倍，在考慮效率問題時，必須將所需計算量也考慮在內.因此，想要提高計算效率，需滿足

2Var(YAV)≤Var(Y1),

(6)

此條件等價于Cov[Y1,Y2]≤0.事實上，Y1和Y2都是模擬所生成的隨機數的函數，BROADIE等[13]指出，只要Y1關于隨機數的函數(記為φ)是單調的，對偶變量法總能起到減小方差的效果.方差縮減比率為

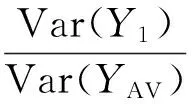
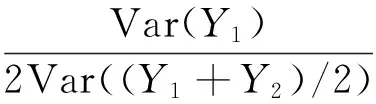
(7)

其中ρ=Cov[Y1,Y2].ρ越小，方差縮減效果越好.對美式期權來說，φ十分復雜，想要計算Y1和Y2的相關系數也很困難，方差縮減效果只能通過模擬來估計.

1.1.2 控制變量法

(8)

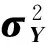
(9)

其中當系數向量b取最優系數向量

時，控制變量YCV的方差取最小值:

(10)

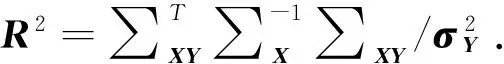
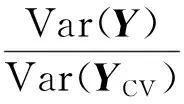
(11)

R2越大，方差縮減效果越好.在實際計算中，最優系數向量的確定步驟為：先用小樣本估計樣本方差SX與樣本協方差SXY，分別代替∑X和∑XY并代入式(10),計算最優系數向量.要求小樣本數目遠小于期權定價的模擬數目.

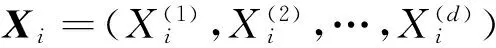
(12)

SXY為d×1矩陣，其第j個元素為

(13)

取股價關于所有模擬路徑的均值，是d維向量.最后重復上述過程，得到N0個估計值，取這N0個估計值的平均值作為最終期權價格估計，取它們的樣本標準差作為該估計的標準差.

1.2 算 法

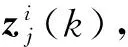
最后，分別結合對偶變量法和控制變量法對求得的估計值做進一步修正，得到最終估計值，并運用批處理方法計算估計量的方差，因為此兩方法都破壞了樣本間的獨立性.

2 數值例子

考慮3個無紅利標的資產的美式看跌期權(d=3)，期權價值由式(2)決定，敲定價格為E.3種資產的初始價格S0為(40,40,40)T，無風險利率r為0.05，資產的波動率分別為0.2,0.3和0.5，到期時間為T，假設標的資產之間的相關系數均為ρ，選取M=1 000,N=10，采用Matlab計算，并用文獻[11]中的例子進行檢驗.

表1分別給出了基本Monte Carlo方法、對偶變量法和控制變量法的計算結果.其中，mean列和std列分別代表重復10次運算的均值和樣本標準差，CI(confidence interval)列為由10次運算結果得到的置信度為95%的置信區間， PDE列是用經典積分方法算得的結果；T的單位為月，資產價格的單位為美元.

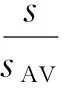
為了分析計算結果的穩定性，下面對3種方法的均值和標準差做進一步比較.選定T=7,E=40，選取ρ=0，1，對前文所述的方法分別重復50次，作散點圖，得到圖1和圖2，圖中每個點都代表10次模擬得到的均值和標準差.

根據散點圖進行橫向比較可得，在3種參數選擇下，對偶變量法和控制變量法都能起到減小方差的作用，對偶變量法縮減效果十分明顯，而控制變量法相對不明顯.縱向比較可得，控制變量法在ρ=1時的方差縮減效果比ρ=0時要高，而對偶變量法則表現得比較平均.其原因為控制變量法的縮減效率取決于控制變量與期權價格的相關程度，相關程度越高，效果越好.在本文中，控制變量為模擬股價，期權收益由股價的最大值決定，故兩者間的相關系數取決于標的資產間的相關系數.當ρ=0時，標的資產間的相關性低，控制變量的縮減效果并不明顯，甚至有幾次模擬的標準差比未使用控制變量的標準差最大值還大.當ρ=1時，標的資產間的相關性高，控制變量和期權收益的相關性也高，控制變量的縮減效果較之前有明顯提高.而對偶變量法的縮減效率由對偶變量產生的估計量的相關系數決定，與到期時間、資產間相關系數等參數無直接關系，所以對偶變量法在不同參數下表現較為平均.

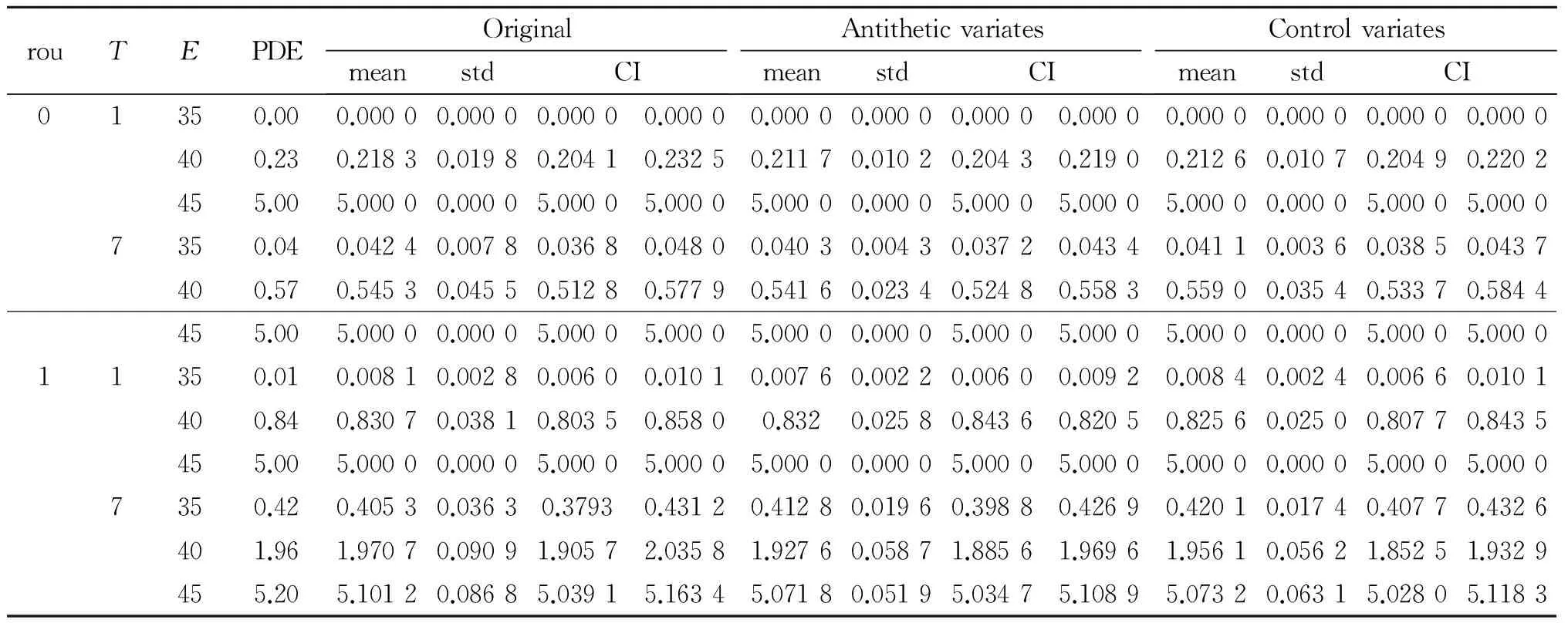
表1 原始方法、對偶變量法和控制變量法的計算結果Table 1 Computing results on original、antithetic variates and control variates methods

圖1 ρ=0,T=7,E=40情形下3種方法的比較Fig.1 Comparison of three methods in the case of ρ=0，T=7,E=40

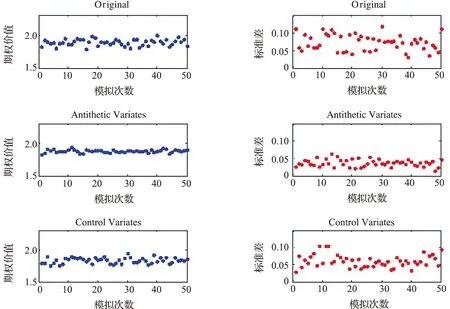
圖2 ρ=1,T=7,E=40情形下3種方法的比較Fig.2 Comparison of three methods in the case of ρ=1，T=7,E=40

rouTEVRERAVVRERCV0135##401.9411.85045##7351.8142.167401.9441.28545##7351.8522.086401.5491.617451.6721.376

3 總 結

充分利用Monte Carlo方法的特點和優勢，討論了一個多目標資產的美式期權定價問題，運用線性回歸思想以及幾何布朗運動和偽隨機數的性質，在LSM方法的基礎上，結合存儲量減小方法和方差縮減技術，對不同參數下美式期權定價進行了比較和分析.采用對偶變量法和控制變量法縮減基本方差，討論了決定其方差縮減效果的因素和參數估計的方法.從計算結果看，對偶變量法較控制變量法標準差縮減效果更明顯，且對偶變量法在不同參數下的表現比較平均，而控制變量法的效果取決于標的資產間的相關系數，這是由所選取的控制變量所決定的.

然而，需要指出的是，本文的計算結果還不夠穩定、收斂性不夠高，這也是 Monte Carlo方法的缺點之一.若采用擬蒙特卡洛方法(quasi-Monte Carlo)，用確定性的低偏差序列 (low discrepancy sequences)代替隨機點列，可改進 Monte Carlo方法的收斂性.如何利用擬蒙特卡洛方法提高算法的收斂性是未來研究的一個重要方向.

[1]JINX,YANGCY.Efficientestimationoflowerandupperboundsforpricinghigher-dimensionalAmericanarithmeticaverageoptionsbyapproximatingtheirpayofffunctions[J].InternationalReviewofFinancialAnalysis,2016,44: 65-77. [

2] BALAJEWICZ M,TOIVANEN J.Reduced order models for pricing American options under stochastic volatility and jump-diffusion models[J].ProcediaComputerScience,2016,80: 734-743.

[3] CHEN W T,XU X,ZHU S P.A predictor-corrector approach for pricing American options under the finite moment log-stable model[J].AppliedNumericalMathematics,2015,97:15-29.

[4] JIN X,LI X,HWEE H T,et al.A computationally efficient state-space partitioning approach to pricing high-dimensional American options via dimension reduction[J].EuropeanJournalofOperationalResearch,2013,231(2):362-370.

[5] HU W B,LI S H.The forward-path method for pricing multi-asset American-style options under general diffusion processes[J].JournalofComputationalandAppliedMathematics,2014,263:25-31.

[6] HU Y H,LI Q,CAO Z Y,et al.Parallel simulation of high-dimensional American option pricing based on CPU versus MIC[J].ConcurrencyandComputation-practice&Experience,2015,27(5): 1110-1121.

[7] BASTANI A F,ZAHMADI Z,DAMIRCHELI D.A radial basis collocation method for pricing American options under regime-switching jump-diffusion models[J].AppliedNumericalMathematics,2013,65:79-90.

[8] LABUSCHAGNE C C A,BOETTICHER S T V.Dupire’s formulas in the Piterbarg option pricing model[J].TheNorthAmericanJournalofEconomicsandFinance,2016,38: 148-162.

[9] YU X S,LIU Q.Canonical least-squares Monte Carlo valuation of American options: Convergence and empirical pricing analysis[J].MathematicalProblemsinEngineering,2014(1)：1-13.

[10] 陳輝.期權定價的蒙特卡羅模擬方差縮減技術研究 [J].統計與信息論壇，2008,23(7): 86-96. CHEN H.Variance reduction techniques of Monte Carlo simulation methods in options pricing[J].Statistics&InformationTribune,2008,23(7):86-96.

[11] BOYLE P,BROADIE M,GLASSERMAN P.Monte Carlo methods for security pricing[J].JournalofEconomicDynamicsandControl,1997,21: 1267-1321.

[12] BARRAQUAND J, MARTINEAU D. Numerical valuation of high dimensional multivariate American securities[J].JournalofFinancialandQuantitativeAnalysis,1995,30: 383-405.

[13] BROADIE M,GLASSERMAN P.Pricing American-style securities using simulation[J].JournalofEconomicDynamicsandControl,1997,21: 1323-1352.

[14] LONGSTAFF F A, SCHWARTZ E S. Valuing American options by simulation: A simple least-squares approach[J].ReviewofFinancialStudies,2001,14(1):113-147.

[15] CHAN R H,WONG C,YEUNG K.Pricing multi-asset American-style options by memory reduction Monte Carlo methods[J].AppliedMathematicsandComputation,2006,179: 535-544.

CHEN Jinbiao, LIN Rongfei

(School of Mathematics & Information Engineering, Taizhou University, Taizhou 317000, Zhejiang Province, China)

American options allow holders to execute an order at any moment before due date. However, the pricing of American options is comparatively complicated because it involves the optimal stopping rule. Monte Carlo method is flexible and easy to implement. Besides, its error estimation and convergence rate are independent of the dimension of the problem, providing Monte Carlo method a great advantage over classical numerical approaches in option pricing. This paper combines the Least Square Monte Carlo method with some variance reduction techniques and a memory reduction approach to price multi-asset American-style options, then compares the efficiency of different variance reduction techniques, and analyzes their application.

Monte Carlo method; American options; variance reduction techniques; pricing

O 242.28

：A

：1008-9497(2017)05-542-06

2017-01-16.

浙江省教育廳一般科研項目(Y201431077)； 浙江省教育廳高等學校訪問學者教師專業發展項目 (FX2016073).

陳金飚(1971-)，ORCID:http://orcid.org/0000-0003-0339-5880,男，碩士，講師，主要從事Monte Carlo 模擬、數據分析、圖像處理等研究.

*通信作者，ORCID:http://orcid.org/0000-0002-4347-0905,E-mail：linrfei@tzc.edu.cn.

10.3785/j.issn.1008-9497.2017.05.008

AMonteCarlosimulationonpricingofhighdimensionalAmericanoptionsbasedonvariancereduction.Journal of Zhejiang University (Science Edition)，2017,44(5)：542-547