Relation between Cartesian product andadjacent vertex distinguishing coloring

WANG Guoxing

(1. Gansu Business Development Research Center, Lanzhou University of Finance and Economics, Lanzhou 730020, China;2. College of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou 730020, China)

Relation between Cartesian product andadjacent vertex distinguishing coloring

WANG Guoxing1,2

(1. Gansu Business Development Research Center, Lanzhou University of Finance and Economics, Lanzhou 730020, China;2. College of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou 730020, China)

Cartesian product; proper edge coloring; proper total coloring; adjacent vertex distinguishing proper edge coloring; adjacent vertex distinguishing total coloring

0 Introduction

The graph coloring has a widely applications in many subject. We only consider simple, finite and undirected graph in this paper.

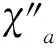
The adjacent vertex distinguishing proper edge coloring of graphs is investigated in several papers[1-6]. The adjacent vertex distinguishing total coloring of graphs is proposed in [7] and studied in several papers[7-16]. Especially, the adjacent vertex distinguishing total chromatic number ofPmKnis obtained in [11] and the adjacent vertex distinguishing total chromatic numbers of the Cartesian products ofPmwithPnandCn, and the Cartesian product ofCmwithCnare given in [13]. We use the usual notation as can be found in any book on graph theory[17].

1 Preliminaries

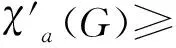
Lemma2[18]χ″=(Cm□Cn)=5(m,n≥3).

From lemma 2, we can obtain the following lemma 3 immediately since anr-regular graphGhas (equitable) total chromatic numberr+1 if and only ifGhas adjacent vertex distinguishing proper edge chromatic numberr+1.

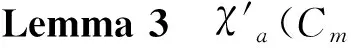
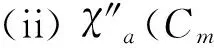
SupposeGis a graph. If a bijectionσfromV(G) toV(G) preserves the adjacency relation, i.e.,σ(u) is adjacent toσ(v) if and only ifuis adjacent tovfor any two distinct verticesuandvofG, thenσis called an automorphism of graphG.

IfGhas an automorphismσ, such that for any vertexv∈V(G),vandσ(v) are adjacent (and thenv≠σ(v)), then we say that graphGis of property (P).

The Cartesian product of two graphsGandH, denoted byG□H, is a graph with vertex setV(G)×V(H) and edge set {(u,v)(u′,v′)|uu′∈E(G),v=v′oru=u′,vv′∈E(H)}.

LetQtdenotet-cube, i.e.,

For two types of adjacent vertex distinguishing colorings of the Cartesian product of a graph with another graph which is of property (P), we will give some important results in section 2 and section 3.

2 The relation between AVDPEC andCartesian product of two graphs

Theorem1SupposeGis a graph without isolated edge andGhas property (P),tis a positive integer.

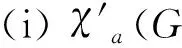
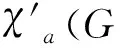
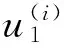
Theorem 1 (i) follows.

(ii) Since for any positive integerl,G□Qlis of property (P) whenGis of property (P), we can obtain (ii) by applying (i) repeatedly .

(iv) We can obtain (iv) by using (iii) repeatedly.

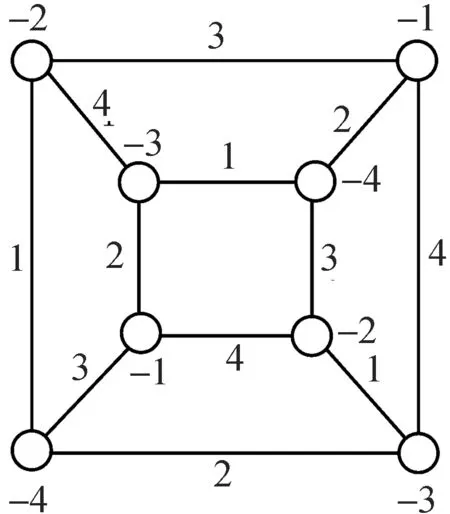
Fig.1 AVDPEC of Q3

Lemma5For any graphG,G□K2has property (P).

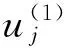
From theorem 1 and lemma 5, we may obtain the following corollary 1.

Corollary1For any graphGwith no isolated edge and integert(≥1), we have

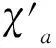
Note that for any graphGand integer numberr(≥3),G□Crhas property (P), so we have the following corollary 2 by theorem 1.

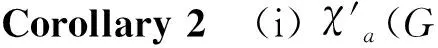
Theorem2Suppose that graphGhas property (P) and has no isolated edge,r(≥4) is an even integer.

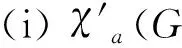
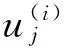
We will give an edge coloring ofG□Crusings+2 colors as follows:

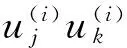
(4) 受注漿施工影響，隧道管片的水平位移和道床沉降在施工前期增長較快，后期增長緩慢；水平收斂和豎直收斂在施工前期增長較慢，而后期增長較快。

From theorem 2, we will obtain the following corollary 3 immediately.

Corollary3Suppose thatGis of property (P) and has no isolated edge,r1,r2,…,rsare even integers at least 4.

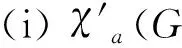
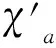
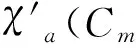
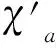
ProofSimilar to the proof of theorem 2(i), we can complete the proof of theorem 3.

3 The relation between AVDTC andCartesian product of two graphs

Theorem4SupposeGis of property (P), andtis a positive integer.

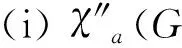
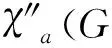
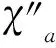
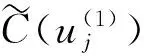
The theorem 4(i) follows.

(ii) Since for any positive integerl,G□Qlis of property (P) whenGis of property (P), we can obtain theorem 4(ii) by applying theorem 4(i) repeatedly.

(iv) We can obtain theorem 4(iv) by using theorem 4(iii) repeatedly.

From theorem 4 and thatG□K2is of property (P), we obtain the following corollary 5.

Corollary5Supposet(≥2) is an integer.

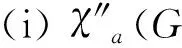
From theorem 4 and thatG□Cris of property (P), we obtain the following corollary 6.

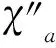
Theorem5Suppose thatGis of property (P),r(≥4) is even.

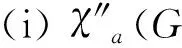
ProofSimilar to the proof of theorem 2, we can complete the proof of theorem 5. The process is easy, so we omitted it.

By generalizing theorem 5, we have

Corollary7SupposeGis of property (P) andr1,r2,…,rs(≥4) are even.

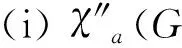
From lemma 4, theorem 4(iv) and corollary 7(ii), we may deduce the following corollary 8.

Corollary8Ifm≥3,n≥3,t≥1,r1,r2,…,rs(≥4) are even, then

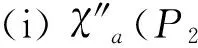
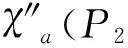
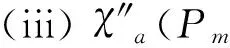
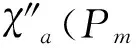
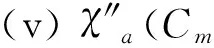
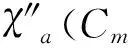
ProofSimilar to the proof of theorem 5(i) or theorem 2(i), we can complete the proof of theorem 6.

[1]BALISTERPN,GY?RIE,LEHELJ,etal.Adjacentvertexdistinguishingedge-colorings[J].SIAMJDiscreteMath,2007,21(1):237-250.

[2] BARIL J L, KHEDDOUCI H, TOGNI O. Adjacent vertex distinguishing edge colorings of meshes[J].AustralasianJournalofCombinatorics,2006,35:89-102.

[4] HATAMI H. Δ+300 is a bound on the adjacent vertex distinguishing edge chromatic number[J].JournalofCombinatorialTheory:SeriesB,2005,95:246-256.

[6] ZHANG Z F, LIU L Z, WANG J F. Adjacent strong edge coloring of graphs[J].ApplMathLett,2002,15:623-626.

[7] ZANG Z F, CHEN X E, LI J W, et al. On adjacent vertex distinguishing total coloring of graphs[J].ScienceinChina(SerA):Mathematics,2005,48(3):289-299.

[8] CHEN X E. Adjacent-vertex-distinguishing total chromatic numbers onK2n+1-E(P3)[J].InternationalJournalofPureandAppliedMathematics,2004,13(1):21-29.

[9] CHEN X E. On the adjacent vertex distinguishing total coloring numbers of graphs with Δ=3[J].DiscreteMathematics,2008,308:4003-4007.

[10] CHEN X E, ZHANG Z F. AVDTC numbers of generalized Halin graphs with maximum degree at least 6[J].ActaMathematicaeApplicataeSinica：EnglishSeries,2008,24(1):55-58.

[11] CHEN X E, ZHANG Z F. Adjacent-vertex-distinguishing total chromatic numbers ofPm×Kn[J].JMathematicalResearchandExposition,2006,26(3):489-494.

[12] CHEN X E, ZHANG Z F, SUN Y R. Adjacent-vertex-distinguishing total chromatic numbers on monocycle graphs and the square of cycles[J].InternationalJournalofPureandAppliedMathematics,2005,18(4):481-491.

[13] CHEN X E, ZHANG Z F, SUN Y R. A note on adjacent-vertex-distinguishing total chromatic numbers forPm×Pn,Pm×CnandCm×Cn[J].JMathematicalResearchandExposition,2008,28(4):789-798.

[14] HULGAN J. Concise proofs for adjacent vertex distinguishing total colorings[J].DiscreteMathematics,2009,309:2548-2550.

[15] SUN Y L, SUN L. The (adjacent) vertex-distinguishing total coloring of the Mycielski graphs and the Cartesian product graphs[C]//7-thChina-JapanConference,DiscreteGeometry,CombinatoricsandGraphTheory. Heidelberg: Springer-Verlag,2007:200-205.

[16] WANG H Y. On the adjacent vertex distinguishing total chromatic numbers of graphs with Δ=3[J].JCombOptim,2007,14:87-109.

[17] BONDY J A, MURTY U S R.GraphTheorywithApplications[M]. New York: Elsevier Science Publishing Co. Inc.,1976.

[18] TONG C L, LIN X H, YANG Y S, et al. Equitable total coloring ofCmCn[J].DiscreteAppliedMathematics,2009,157:596-601.

王國興1，2

(1.蘭州財經大學 甘肅商務發展研究中心，甘肅 蘭州 730020；2.蘭州財經大學 信息工程學院， 甘肅 蘭州 730020)

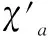
Cartesian積;正常邊染色;正常全染色;鄰點可區別邊染色;鄰點可區別全染色

O 157.5

：A

：1008-9497(2017)05-520-06

date：Dec.26, 2016.

Supported by the National Natural Science Foundation of China (61662066), Gansu Business Development Research Center Project of Lanzhou University of Finance and Economics(JYYY201506) and Key Science and Research Project of Lanzhou University of Finance and Economics(LZ201302).

Abouttheauthor:WANG Guoxing(1976-),ORCID:http://orcid.org/0000-0001-6582-650X, male, master, associate professor, the field of interest are the graph theory and its applications,E-mail: wanggx@lzufe.edu.cn.

10.3785/j.issn.1008-9497.2017.05.004

Cartesian積與鄰點可區別著色之間的關系.浙江大學學報(理學版),2017,44(5):520-525