一類可積晶格方程族的可積性探究
(山東科技大學 山東 青島 266590)
一類可積晶格方程族的可積性探究
孫士麗
(山東科技大學 山東 青島 266590)
近年來,非線性離散可積系統作為描述非線性現象的有力工具,受到了人們的廣泛關注。本文提出了一個新的離散的4×4的矩陣譜問題,利用離散的零曲率方程表示法構造了一族新的離散的可積系統,并研究離散可積系統的劉維爾可積性。
離散可積系統;晶格方程族;零曲率方程;可積性
一、引言
可積晶格方程用來描述自然科學中許多復雜的現象。例如,晶體中的質點振動,食物鏈中的脈沖,電網的電流等,數學家們已經從不同的角度進行了系統的研究,如連續極限和r-矩陣結構[1],反散射變換,對稱和主對稱[2],可積耦合,達布變換等。
一類離散空間譜問題(1)
Eφn=Un(un,λ)φn
和相應的時間譜問題(2)
φn,t=V(n)(un,λ)φn
如果一個晶格方程(3)
un,t=K(un,un-1,un+1,...)
是(1)和(2)的一個兼容性條件,那么它在Lax意義下可積,也就是(4)式
Un,t=(EV(n))Un-UnV(n)
我們稱方程(1)、(2)是晶格方程(1)的一個Lax對。尋找新的可積晶格方程族,使其滿足離散譜問題(1),這仍然是一個復雜的任務。
在文章第2節中,介紹一類離散譜問題(5)
這里un是位勢向量,φn是本征函數,λ是譜參數且λt=0。不難發現,譜問題(5)也等價于一個特征值問題。首先,我們要選擇合適的時間譜問題,然后由離散零曲率方程導出一個可積晶格方程族。最后,在第3節中,做一些評價和總結。
二、一類新的可積晶格方程族
在這一節中,我們將推導出一個新的可積晶格方程族。首先,我們求解靜態的離散零曲率方程(6)
(EΓn)Un-UnΓn=Γn+1Un-UnΓn=0
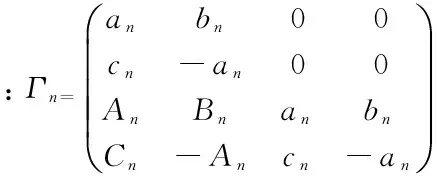
由方程(6) 并利用勞倫級數展開式我們得到初始條件:
和遞推關系(8)式(m≥0):

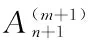



我們引入輔助譜問題(10):
那么,該方程與方程(5)的相容性條件表示為:
(Eφn)tm=E((φn)tm)
它等價于離散的零曲率方程
求得微分差分方程族的可積系(11)
所以譜問題(5)和方程(10)構成方程(11)的Lax對。當m = 0,方程(11)變成一個簡單的線性系統rnt0=0,snt0=0。我們得到方程(11)的第一個非平凡的可積晶格方程,當m = 1時,得(12)式:
rnt1=rn(snrn-1)-rn-1(sn-1rn-1-1),snt1=rn+1-rn,

三、結論
在本文中,我們介紹了一個離散譜問題,并由離散零曲率方程推導出一個離散可積微分差分方程族。此外,還有其他的可積性問題值得進一步研究,例如達布變換、對稱和主對稱、可積耦合系統、半直和李代數等。
[1]董煥河,張玉峰.孤立子理論與可積系統[M].2006
[2]李翊神.孤子與可積系統[M].1999
孫士麗(1991-),女,漢,山東臨沂,碩士,山東科技大學數學與系統科學學院,微分方程理論及應用。

