基于前饋解耦的永磁同步電機控制系統研究

，，，，

(1.新疆大學電氣工程學院 教育部可再生能源發電與并網控制工程技術研究中心，新疆 烏魯木齊 830046； 2.金風科技股份有限公司，新疆 烏魯木齊 830026)

基于前饋解耦的永磁同步電機控制系統研究

荊世博1，王維慶1，王海云1，吳先友2，蔣中川2

(1.新疆大學電氣工程學院 教育部可再生能源發電與并網控制工程技術研究中心，新疆 烏魯木齊 830046； 2.金風科技股份有限公司，新疆 烏魯木齊 830026)

由于永磁同步電機(PMSM)的前饋解耦采用雙閉環的控制器，其全系統的傳遞函數已高于二階，導致了控制器參數整定困難。通過分析PMSM以及其解耦控制的速度環和電流環的數學模型，提出了雙閉環控制器中被控制量與PMSM數學模型之間的聯系，構造出了基于拉氏變換的全系統簡化模型，為雙閉環控制器的PI參數整定提供了理論依據。針對已構建的全系統傳遞函數模型的高階特性，提出了根據勞斯穩定判據來整定PI參數的方法，并在Simulink中進行了實驗仿真。仿真結果表明，整定后的參數能夠使系統快速趨于穩定，并且具有較好的魯棒性。

永磁同步電機(PMSM)；前饋解耦；簡化模型；勞斯穩定判據

0 引 言

PMSM由于其可靠性高、體積小、控制簡單等優點，已經取得了廣泛的應用[1]。在PMSM的控制中多采用矢量或直接轉矩的控制策略，由于直接轉矩的控制方法存在轉矩脈動和調速范圍窄的問題，在現用的交流伺服系統中一般采用矢量控制[2-3]。

矢量控制一般由電流內環和轉速外環構成，其控制策略是利用解耦控制得到近似線性化的模型。矢量控制有多種實現方法，如電流反饋控制、電壓前饋控制等[4-6]。考慮到電流反饋控制策略實現方便，控制簡單，在電機的控制中一般采用較多[7-8]。在電流反饋控制策略中，電流的控制精度直接影響到轉矩控制的精確性和快速性，在實際的電機控制策略中多采用傳統的PI控制器來進行電流環和速度環控制。在PI控制器的參數整定中，其整定方法多是依據經驗得出，需要反復的試湊。

下面依據PMSM的數學模型與前饋解耦控制器的簡化模型，得到PMSM與電流內環和速度外環的傳遞函數。根據勞斯穩定判據，提出了控制器PI參數整定的方法。仿真表明，根據勞斯穩定判據得到的控制器參數有快速的響應特性，對于系統輸入扭矩的波動有較好的魯棒性，并且能夠在較短的時間內使系統趨于穩定。

1 PMSM的數學模型

為便于分析,假設：

1) 轉子上的永磁體產生主磁場，轉子上無阻尼繞組；

2)忽略齒槽、換相過程和電樞反應等的影響；

3)電樞繞組在定子內表面均勻連續分布；

4)磁路不飽和, 不計渦流和磁滯損耗。

PMSM采用三相星形連接，且沒有中線，可得永磁同步電機在d、q軸坐標系下的電壓方程與轉速方程為[9-10]

(1)

式中:R為電機的等效電阻；ω為轉子機械角速度；p為磁極對數；Tm為電機的機械扭矩；F為摩擦系數；Te為電機的電磁扭矩；J為轉子的慣性系數；λ為永磁體磁鏈；id、ud為d軸的電流和電壓；iq、uq為q軸的電流和電壓；Ld、Lq為直軸和交軸電感，采用表面貼裝式電機，Ld=Lq。

2 PMSG傳統控制器設計

傳統的PMSG的控制策略采用PI控制器對電機測量反饋的d、q軸電流進行對立的調節。為了便于分析，假設電壓型逆變器(VSI)沒有延遲現象，即VSI所等效一階慣性傳遞函數的時間常數為0。傳統PMSG及控制的拓撲圖如圖1所示。

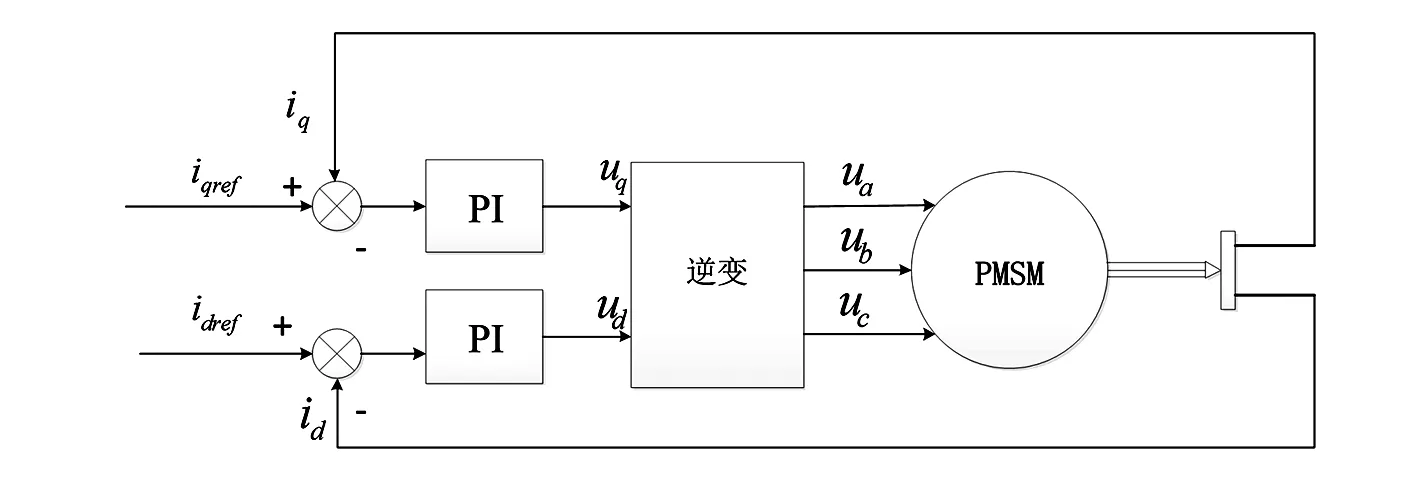
圖1 傳統PMSG控制策略

在圖1的逆變環節中，采用滯環控制生成ua、ub、uc。以q軸為例進行分析，建立q軸等效框圖如圖2所示。

忽略逆變器的延遲效應，列寫如圖2所示的傳統PMSG的控制策略的開環傳遞函數：

(2)

由以上分析可知，傳統PMSG控制系統的開環

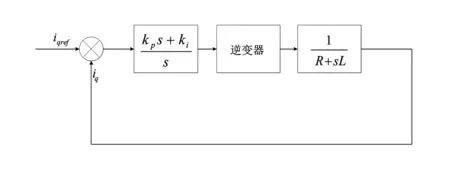
圖2 傳統PMSG等效控制框圖

傳遞函數為二階。關于阻尼比ξ：當取臨界阻尼時，系統具有最理想的響應時間，且響應速度也最快，但在穩定后，將出現等幅震蕩；當阻尼比為過阻尼時，系統將不會出現超調量，并能夠最終穩定在設定值，但過阻尼沒有超調量是以犧牲調節時間為代價，因此其調節時間較長；欠阻尼的各種情況介于兩者之間。綜合臨界阻尼、過阻尼和欠阻尼的情況，考慮到阻尼比越小，系統的超調量也就越大，但相應的調節時間也就越短，一般取0.4～0.8，這里ξ取0.707。系統的截止頻率定為1 000 π。

傳統的電流控制器結構簡單并且方便建立系統的模型，但忽略了PMSG本體作為控制對象，其a、b、c三相電流經3s/2r變換后，d軸和q軸電流之間的強耦合關系，造成系統的調節時間較長。單純地依靠PI控制器的調節作用對電機進行控制，往往不能滿足控制性能的要求。

3 基于前饋解耦的永磁同步電機PI控制器的設計

3.1 PMSM前饋解耦補償型電流控制的模型

從式(1)中，可以看出電流的d軸和q軸的電流分量之間存在相互耦合，增加了控制器的設計難度。傳統的PI控制器雖然結構簡單，控制方便，但其忽略了d軸分量與q軸分量之間的交叉耦合。通過對式(1)中電流分量耦合項的補償，可以提高控制器的動態性能和控制精度。d軸、q軸耦合項補償項如式(2)所示。

(2)

基于前饋解耦補償的PMSM控制系統通常采用電流內環與轉速外環的控制結構。在轉速外環中，電機的機械轉速通過速度傳感器進行測量并與參考轉速ωref進行比較，產生轉速偏差信號，此偏差信號經速度外環的PI控制器調節后作為q軸電流分量的參考值iqref。給定d軸電流分量的參考值idref≡0。將得到的d軸與q軸的電流參考信號與電機定子的三相電流實時測量值經3s/2r變換后的id、iq進行比較，得出d軸、q軸電流分量的偏差值。此偏差值經前饋解耦控制器調節后生成直軸和交軸的電壓信號Ud、Uq。將其進行2r/3s變換產生PWM控制信號并送入到三相逆變器中，控制三相逆變器的開關狀態，進而控制PMSM輸出的三相電壓與電流。

由以上分析可得前饋解耦補償控制策略如圖3所示。

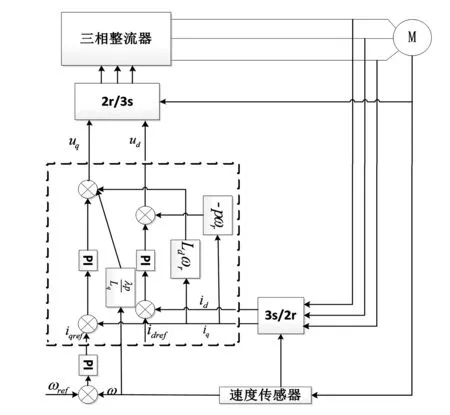
圖3 前饋解耦補償控制策略

3.2前饋解耦控制器的設計

采用d軸電流分量idref≡0的控制方式。將式(3)帶入式(1)，可得d軸與q軸的電壓方程為

(4)

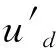
由于Ld=Lq，式(1)的PMSM扭矩方程可表示為

(5)

將式(5)帶入式(1)中，可得轉速ω與q軸電流分量iq的關系式為

(6)

根據以上的分析，可得q軸電流的傳遞函數框圖如圖4所示。

圖4 q軸電流等效傳遞函數框圖

根據式(4)所表述的q軸電流方程建立圖4虛線框中的電流內環。這里采用了idref≡0的控制方式，因此，在q軸電流內環的傳遞函數中不再表述d軸電流分量在q軸電流的耦合項。由于靜止坐標與旋轉坐標的Clark和Park變換只是數學上的理論變換，并且其變換的依據正是基于功率不變的約束，因此在q軸等效的傳遞函數中不需要列寫Clark和Park變換環節。

以圖4中左側PI控制器的輸出作為電流內環的輸入，q軸電流分量iq作為輸出，可得q軸電流內環的傳遞函數為

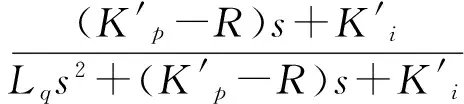
(7)

圖4中虛線框之外的系統為q軸電流矢量的轉速外環，其輸入量為機械扭矩Tm，輸出為電磁扭矩Te，將輸出的電磁扭矩作為扭矩輸入的參考值送入速度內環，從而建立速度外環與電流內環之間的聯系。從圖4可以看出，q軸的電流內環是單輸入單輸出(SISO)的系統，將其作為一個傳遞函數模塊加入到速度外環的模型中，見圖5，可得雙閉環傳遞函數。

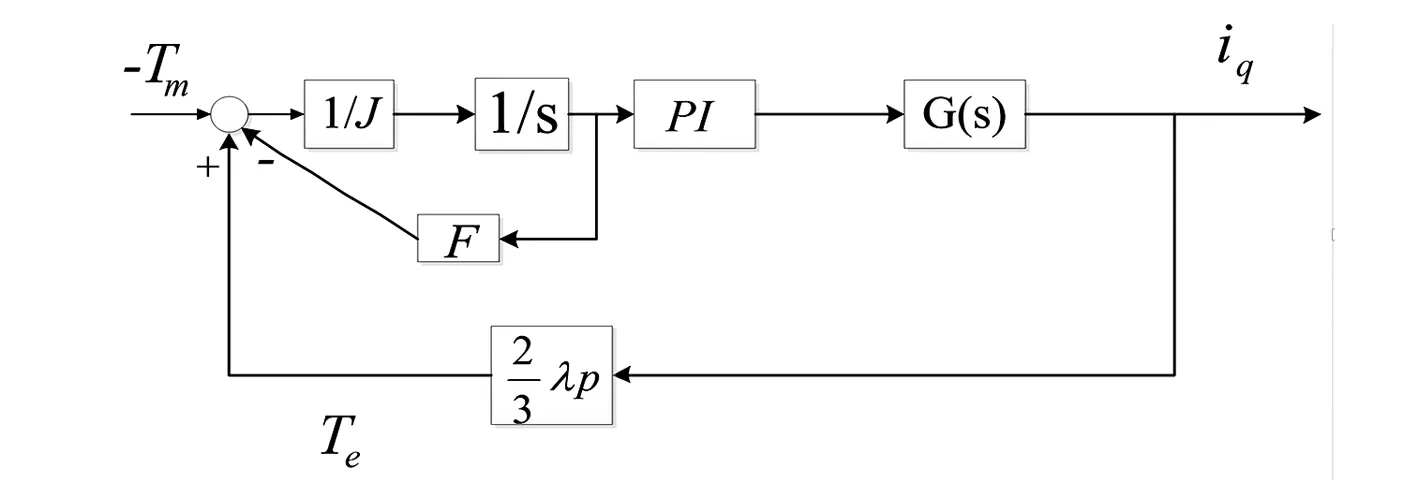
圖5 q軸矢量控制的速度外環

令M(s)為前向通道的傳遞函數，q軸速度外環傳遞函數方程為

(8)

對式(8)進行化簡，得到全系統的閉環傳遞函數為

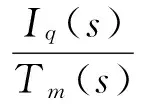
(9)

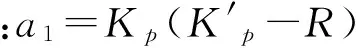
穩定作為控制系統重要的性能指標，也作為系統能夠正常運行的首要條件，如果系統不穩定，就會在任何微小擾動作用下偏離原來的平衡狀態，并隨著時間的推移而發散。任何系統在擾動的作用下，都會發生偏離平衡狀態的現象，產生偏差。因而，分析系統的穩定性是控制理論的基本任務之一。對于一階或二階系統，可以通過求解系統特征根的方法來判定系統的穩定性，但高階系統的求根工作量是很大的[11]。通常的方法是借助勞斯穩定判據來判定高階系統的穩定性。

由式(9)可知PMSM全系統的特征函數為

H(s)=b1s4+b2s3+b3s2+b4s+b5

(10)

列寫系統的勞斯表如表1所示。

表1 PMSG q軸電流傳遞函數勞斯表

根據永磁同步電機的參數，由勞斯穩定判據的充要條件求解勞斯表中的第一列元素，使其全部大于0，即可得到轉速內環和電流外環的PI參數范圍。d軸電流分量采用的相同的方法，具體的整定過程不再贅述。

(a)轉速波形

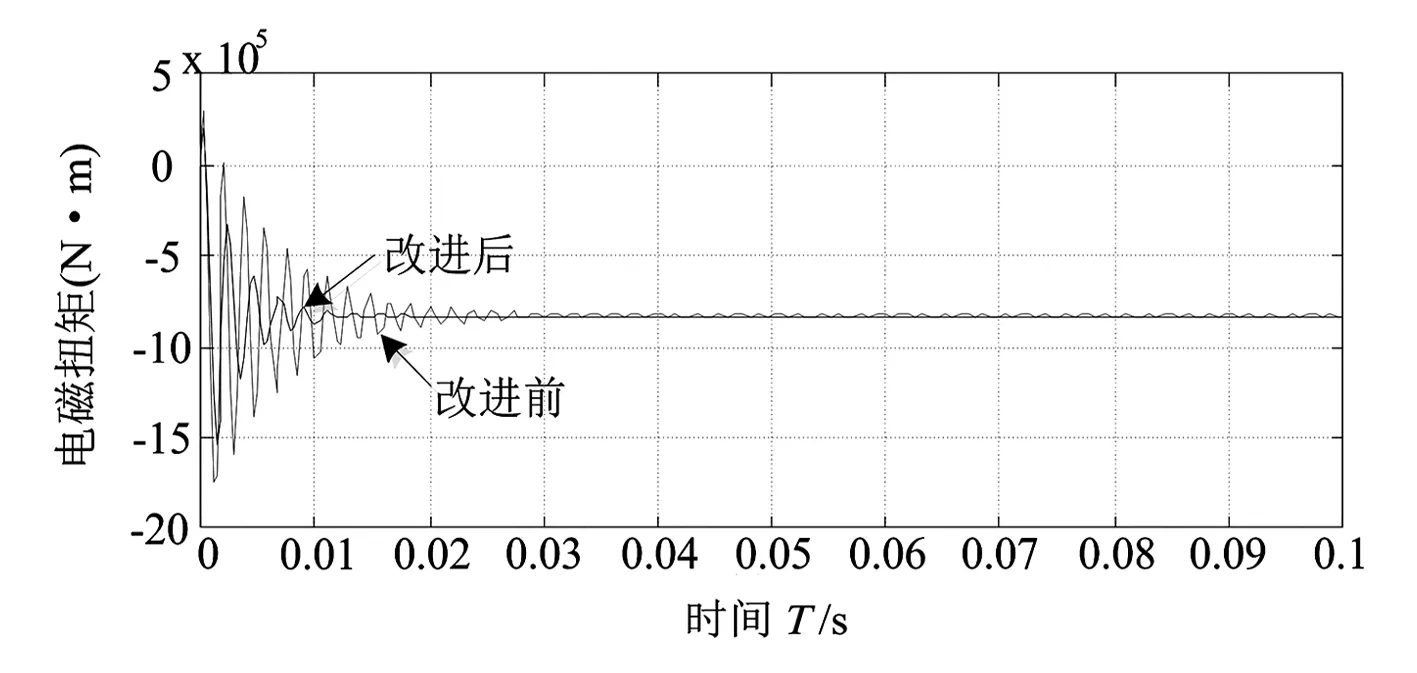
(b)電磁扭矩波形

(c)q軸電流波形

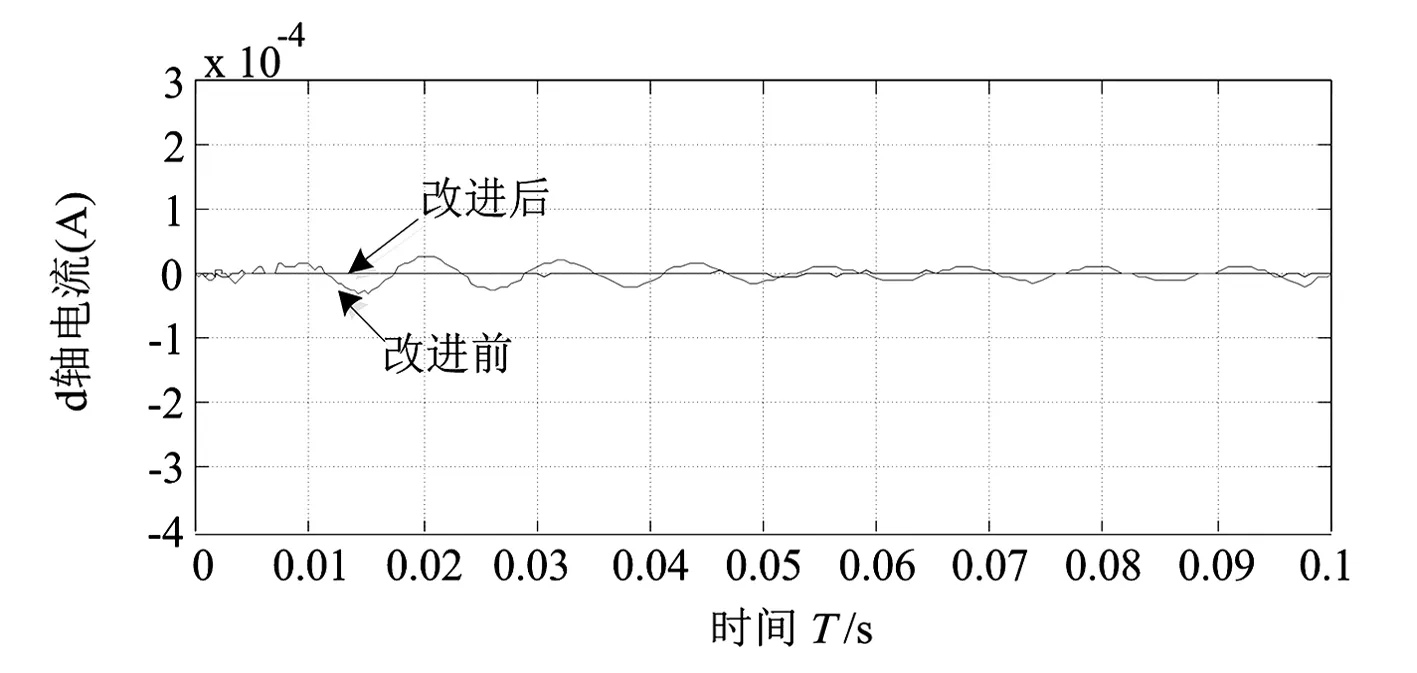
(d)d軸電流波形

(e)機械扭矩變形波圖6 仿真波形

4 仿真驗證及分析

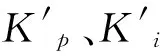
運行仿真模型，得到PMSM的機械轉速、電磁扭矩以及d軸與q軸的電流波形。為了測定整定得到的PI參數對系統輸入量發生突變時的魯棒性以及其對扭矩變化的響應速度，在PMSM系統穩定運行0.5 s時，使電機的機械扭矩發生躍變，觀測其在參數躍變后的扭矩波動的波形。仿真波形見圖6。

相比改進前的控制策略，改進后的前饋解耦控制方案，對d軸和q軸之間的耦合量pωiq、-pωiq與λpω/Lq進行了補償，使d軸和q軸分量中不再出現耦合項。

4 結 論

在分析傳統控制方法的基礎上，考慮到d軸和q軸的耦合，提出前饋解耦的控制策略，并針對前饋解耦補償控制的PMSM全系統進行了分析，得出了基于q軸電流分量的雙閉環系統與PMSM數學模型之間的聯系以及簡化的傳遞函數模型。由于其傳遞函數為高階方程，控制理論中針對一階和二階的求解特征根的方法已不再適用，提出利用勞斯穩定判據來整定控制器參數范圍的方法。仿真結果表明，依據得出的全系統簡化傳遞函數能夠有效實現控制目標，并且在輸入量發生變化時，能使系統快速達到穩定狀態并對系統變化有較好的魯棒性。然而基于勞斯穩定判據整定的PI參數，并不能得到精確的比例和積分參數，需要進行多次的調試是所提方法需要改進的研究方向。

[1] 李政，胡廣大，崔家瑞，等.永磁同步電機調速系統的積分型滑模變結構控制[J].中國電機工程學報，2014，34(3)：431-437．

[2] 耿翠紅，曹以龍.基于DSP的PMSM矢量控制系統的硬件和軟件實現[J].電力電容器與無功補償，2014，35(1)：30-33．

[3] 郭磊磊，張興，楊淑英，等.一種改進的永磁同步發電機模型預測直接轉矩控制方法[J].中國電機工程學報，2016，36(18)：1-9．

[4] Bimal K.Bose.現代電力電子學與交流傳動[M].北京：機械工業出版社，2005．

[5] 唐小琦，白玉成，陳吉紅.永磁同步電機高性能電流解耦控制的研究[J]．電氣傳動，2009，39(10)：18-22．

[6] 陳榮．永磁同步電機控制系統[M].北京：中國水利水電出版社，2009．

[7] P Krause，O Wasynczuk，S Sudhoff，et al．Analysis of Electric Machinery and Drive Systems[M]．IEEE Press，2002．

[8] D Grenier,L A Dessaint，O Akhrif，et al． Experimental Nonlinear Torque Control of a Permanent-magnet Synchronous Motor Using Saliency[J].IEEE Transactions on Industrial Electronics,1997,44(5):680-687．

[9] 李三東，薛花，紀志成．基于Matlab永磁同步電機控制系統的仿真建模[J]．江南大學學報(自然科學版)，2004，3(2)：115-120．

[10] 黃知超，楊升振，延紅艷，等.基于dq坐標系有功無功電流解耦空間電壓矢量的STATCOM控制方法[J].電測與儀表，2012，49(12)：32-36．

[11] 胡壽松.自動控制原理[M]．北京：科學出版社，2008．

[12] 黃一，張文革．自抗擾控制器的發展[J]．控制理論與應用，2002，19(4)：485-492.

As the feedforward decoupling of permanent magnet synchronous motor (PMSM) adopts double closed-loop controller, its system-wide transfer function is higher than that of second order, which leads to the difficulty of controller parameter setting. By analyzing the mathematical model of velocity loop and current loop of PMSM and its decoupling control, the relationship between the control quantity and the mathematical model of PMSM in double closed-loop controller is obtained, and the whole system based on Laplace transform is constructed, which provides a theoretical basis for the PI parameter setting of double closed-loop controller. Aiming at the high-order characteristic of the constructed system-wide transfer function model, the range of PI parameters is set according to Rouse stability criterion, and the experimental simulation is carried out in Simulink. The simulation results show that the parameters after setting can make the system become stable quickly and have good robustness.

permanent magnet synchronous motor (PMSM); feedforward decoupling; simplified model; Routh stability criterion

國家自然科學基金項目(51667020)

TM351

：A

：1003-6954(2017)04-0074-05

2017-03-04)

荊世博(1989)，碩士研究生，主要研究方向為可再生能源并網技術； 王維慶(1959)，博士、教授、博士生導師，研究方向為電力系統自動化和風力發電機組的智能控制。