具備不平衡運行控制直驅風機對近區系統負序電流的影響

，，

(1.西南交通大學電氣工程學院,四川 成都 610031； 2.國網四川省電力公司電力科學研究院,四川 成都 610072)

具備不平衡運行控制直驅風機對近區系統負序電流的影響

徐紅燦1，滕予非2，王曉茹1

(1.西南交通大學電氣工程學院,四川 成都 610031； 2.國網四川省電力公司電力科學研究院,四川 成都 610072)

針對具備不平衡運行控制的直驅永磁同步風電機組(direct-driven permanent magnet synchronous generators，DDPMSG)，提出了一種負序電流注入下，含直驅風機系統的穩態不對稱計算方法。在正負序網中，將直驅風機等效為受控電流源，然后根據系統正負序網，列出系統正負序電壓電流方程，與直驅風機正負序電流指令值計算方程聯立求解，得到系統各參數的序分量。從理論上分析了直驅風機對近區系統負序電流的影響，研究結果表明，相比同步電機，直驅風機使系統其他支路輸出的負序電流更大。在雙機無窮大以及十三節點配電網的算例中，通過理論計算值與仿真值的對比，驗證了所提計算方法和結論的正確性。

直驅風機；負序電流；不平衡運行控制；同步電機

0 引 言

在環境與能源問題日益加劇的背景下，風力發電因其清潔可再生的特點得到快速發展。直驅永磁同步風電機組(direct-driven permanent magnet synchronous generators，DDPMSG)具有效率高、故障率低、運維成本低等優點，近年來成為主流風電機型之一[1]。

中國適合大規模開發風電的地區一般都遠離負荷中心，甚至遠離主干電網，使得風電機組所聯的電網實質上是一個存在電壓跌落、電壓不平衡、諧波畸變等各種運行風險的“弱電網”[2]。電網不平衡會惡化直驅風機的運行性能，造成風機饋入電網的功率發生2倍于電網頻率的波動，并導致直流側電壓發生振蕩[3-4]。因此需要改進風機控制策略，提高其在電網不平衡下的運行性能。

針對電網不平衡下直驅風機的運行控制，文獻[4,6-7]等采用了一種基于雙旋轉坐標系的正負序電流控制，根據不同的控制目標產生正負序電流指令值，實現輸出功率穩定控制、負序電流抑制等控制目標。

與傳統同步發電機不同，逆變型分布式電源(inverter interfaced distributed generation，IIDG)在故障時的輸出特性，主要取決于其采用的控制策略[8]。逆變器內部跟蹤電量主要有電壓和電流兩種，在分析計算時，可以分別等效為受控電壓源和受控電流源[9]。

已有文獻對電網不平衡下逆變型電源的分析計算展開了研究。文獻[9]考慮故障中IIDG序電流控制和無功功率支撐，認為IIDGs短路電流與并網點電壓、并網運行時間有關，建立了包含負序電流的IIDG短路序分量電流源模型，提出多IIDGs系統的短路電流迭代算法。文獻[10]假設變流器控制和鎖相環理想工作下，認為IIDG在不同故障下均只輸出正序電流，而無負序或零序電流，進而給出了輸出故障電流的表達式。文獻[11]指出正序分量控制下逆變型分布式電源在不對稱故障時不輸出負序電流，提出了計及控制特性的IIDG壓控電流源等值模型，并給出了求解含IIDG配電網節點電壓方程的方法。文獻[12]基于并網逆變器抑制輸出有功功率波動的控制策略，給出了具備不對稱故障控制策略的逆變型電源，在不對稱故障下的穩態短路電流公式，并通過仿真對比驗證。

然而，針對弱聯系電網中常見的系統含有負序電流的輕度不平衡工況下，含直驅風機系統的不對稱計算尚少見報道。基于此，提出了一種含直驅風機系統穩態不對稱計算方法，在正負序網中將直驅風機等效為受控電流源，通過聯立系統正負序電壓電流方程及直驅風機不平衡控制中電流指令計算方程，求解系統參數各序分量。同時從理論上分析了直驅風機對近區系統負序電流的影響，通過理論計算與仿真對比，驗證了計算方法與結論的正確性。

1 直驅風機不平衡運行控制原理

DDPMSG一般采用背靠背變流器并網，其中網側變流器的典型原理如圖1所示。變流器經LCL濾波器并網。

圖1中：Lf、Lg、Cf分別為變流器側電感、網側電感及濾波電容；Rc為串聯阻尼電阻；Cdc、udc分別為直流電容及其電壓；eabc、igabc分別為三相電網電壓和三相并網電流。

當電網出現不平衡時，變流器網側復功率S為[13]

S=Pg+jQg=(Pg_0+Pg_c2cos2ωt+Pg_s2sin2ωt)+
j(Qg_0+Qg_ccos2ωt+Qg_s2sin2ωt)

(1)

式中，Pg、Qg分別為有功、無功功率；下標0、s2、c2分別代表功率的平均分量和二倍頻正、余弦波動分量；ω為同步電角速度。由此可見，該工況下變流器網側有功功率和無功功率都含有二次諧波分量，引起電網出現功率波動。

將式(1)進行派克變換，可以得到同步旋轉dq坐標系下，功率各分量表達式為

(2)

式中，e、ig分別為電網電壓、并網電流；上標+、-分別代表正序、負序分量；下標d、q分別代表同步旋轉坐標系下的d、q分量。

由式(2)可知，網側變流器輸出功率的平均值及二倍頻分量與并網電流正、負序下dq軸4個分量有關，因此，令Pg_s2*=Pg_c2*=0，并將其代入式(2)，即可通過控制正、負序電流，消除有功功率二倍頻波動；同時，控制平均無功功率為0，實現單位功率因數控制，可以得到并網電流的指令值為

(3)

式中，Pg_0*為變流器平均有功功率指令，其與直流電容電壓平均值有關。當直流電容電壓采用PI控制器時，控制器輸出為直流電容支路電流指令值，進而可得

(4)

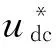
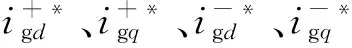
2 負序電流注入下含直驅風機系統序網分析

2.1具備不平衡運行控制的直驅風機序網模型

逆變器內部跟蹤變量主要有電壓和電流兩種，根據其不同，將逆變器分為電壓控制型和電流控制型，在分析計算中，可以分別等效為受控電壓源和受控電流源。這里采用電流控制，因而可以將直驅風機等效為受控電流源。

直驅風機經箱式變壓器并網，變壓器的低壓側通常采用星形不接地或者三角形接線方式，不存在零序通路，因此在序網分析中，不考慮零序網絡。

由于變流器調節時間很短，在分析直驅風機穩態輸出時，可以忽略電流控制內環，認為實際電流等于電流指令值，則有

(5)

進而可得

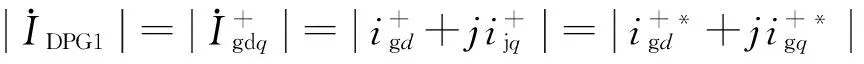
(6)

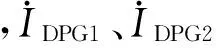
2.2負序電流注入序網模型

由于風電富集地區常遠離電網負荷中心，因此

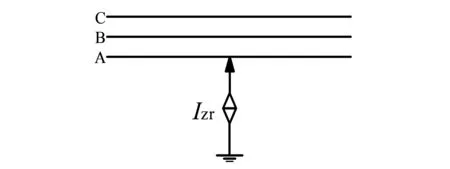
圖2 負序電流注入方法

風電場所聯為弱聯系電網，存在三相不平衡、電壓跌落等運行風險。電網不平衡會使系統中產生負序電流，下面通過往系統注入負序電流的方式，來模擬電網輕度不平衡的工況。具體方式如圖2所示。

在注入點的A相注入電流Izr，可得注入電流所在支路三相電流為

(7)

進而可得，三序電流為

(8)

2.3含直驅風機系統不對稱計算原理

基于上述分析，在負序電流注入下，對于任一常規系統，接入具備不平衡運行控制的直驅風機，采用對稱分量法，忽略零序網絡，可以得到其正、負序網絡如圖3所示。

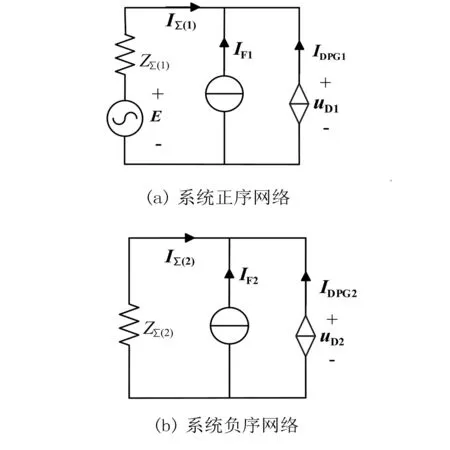
圖3 含直驅風機系統的正、負序網

圖3中，E為系統等效正序電壓；I∑(1)、I∑(2)分別為系統等效正、負序電流；Z∑(1)、Z∑(2)分別為系統除直驅風機外的等效正、負序阻抗；uD1、uD2分別為直驅風機出口電壓的正、負序分量。

基于基爾霍夫電壓、電流定律，不難推算出

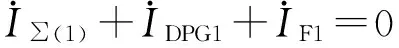
(9)

可見，負序電流注入下，含直驅風機系統的不對稱計算原理為：首先求得系統的正、負序等效阻抗，其次列出各序電壓、電流方程式(9)，然后結合直驅風機序網模型式(3)、式(6)以及負序電流注入序網模型式(8)，聯立求解，即可求解各序分量的穩態值。2.4與同步電機對比

在分析風電并網對系統的影響時，通常會將風電機組替換為同等容量的常規同步電機，通過兩者的比較來進行分析。

相似的，在研究直驅風機對近區電力系統負序電流的影響時，將直驅風機替換為同等容量的同步電機。替換后，系統的負序網絡如圖4所示。

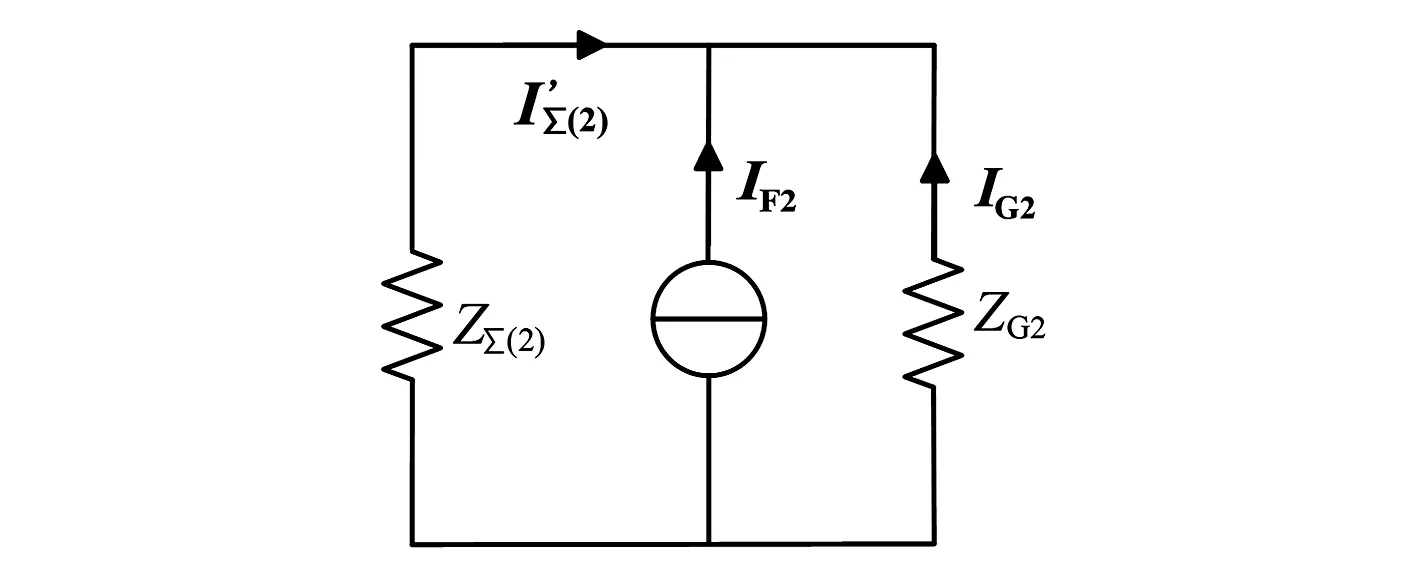
圖4 替換為同步電機后系統負序網絡

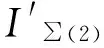
由圖4及式(9)可以推出

(10)

由式(10)可知，在負序電流注入下，直驅風機的接入為系統增加了一個負序源；同時，相比于同步電機，直驅風機并不分擔注入的負序電流。因此，直驅風機相比于同步電機，使近區電力系統的其他支路輸出更大的負序電流。

3 算例分析

針對包含直驅風機與同步電機的雙機無窮大系統和十三節點配電網系統，在負序電流注入的工況下，采用提出的不對稱計算方法求解系統各序分量的穩態值。并將直驅風機置換為同步電機，通過比較研究直驅風機對系統負序電流的影響。將理論計算結果與PSCAD軟件中電磁暫態仿真結果進行對比驗證。

3.1雙機無窮大系統

風電機組對系統中傳統電源的影響常受到研究人員的關注。建立直驅風機與同步電機并列的雙機無窮大系統見圖5。

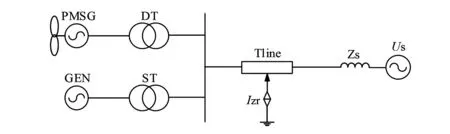
圖5 直驅風機與同步電機并列系統

如圖5所示，直驅風機與同步電機都經變壓器和傳輸線接入無窮大系統，負序電流在傳輸線中點注入。圖6給出了并列系統正、負序網絡。

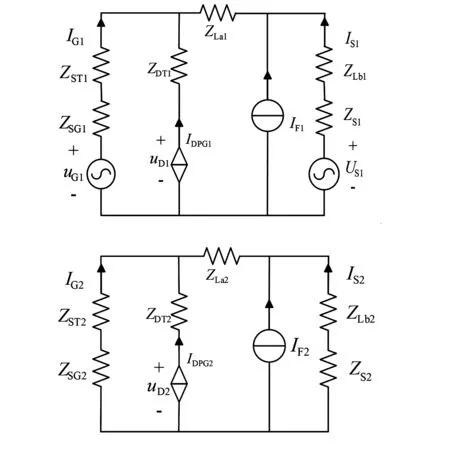
圖6 雙機無窮大系統正、負序網絡

根據圖6得到電壓電流方程如下：

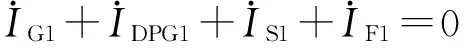
(11)

式中：ZS為電源等效阻抗；US1為電源正序電壓；ZLa、ZLb分別為注入點左、右兩邊傳輸線阻抗；ZDT為風機出口箱變阻抗；ZST為同步機出口箱變阻抗；下標1、2分別表示參數正負序分量。

進而通過所提出的不對稱計算方法計算系統各主要變量的序分量，在MATLAB中進行理論計算，同時在PSCAD進行仿真分析。仿真參數如表1所示。

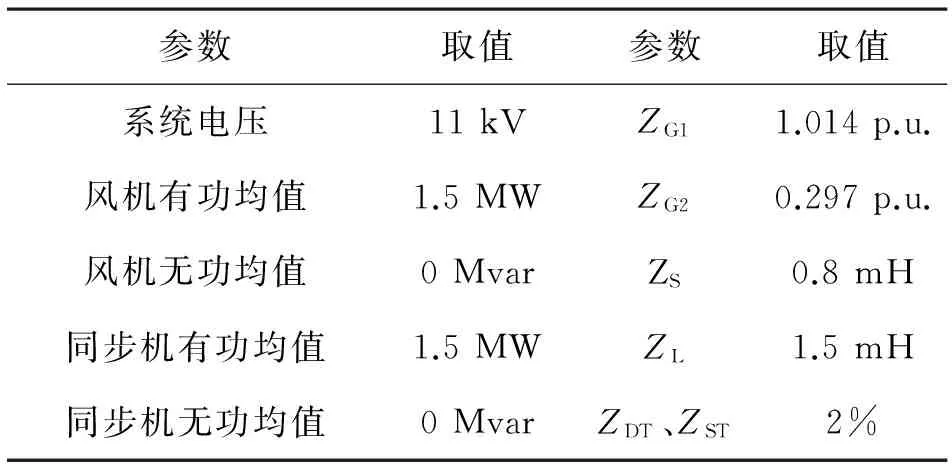
表1 仿真系統主要參數

設置10 s時，在傳輸線中點的A相注入電流1∠120° p.u.，系統主要變量的MALTAB計算值與PSCAD仿真值對比如表2所示。

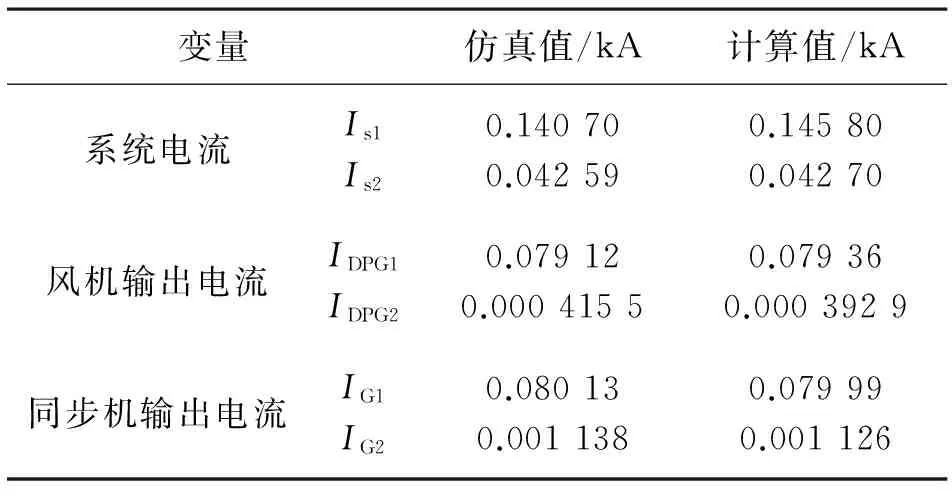
表2 雙機無窮大系統主要變量對比

由表2可知，系統各主要變量的仿真值與計算值十分接近，驗證了所提不對稱計算方法的正確性。

將直驅風機替換為同等容量的同步電機B，建立雙同步電機無窮大系統，再次進行條件相同的仿真，結果如表3所示。對比表2與表3可知，與同步電機相比，直驅風機使并列同步電機輸出負序電流更大，驗證了理論分析的正確性。

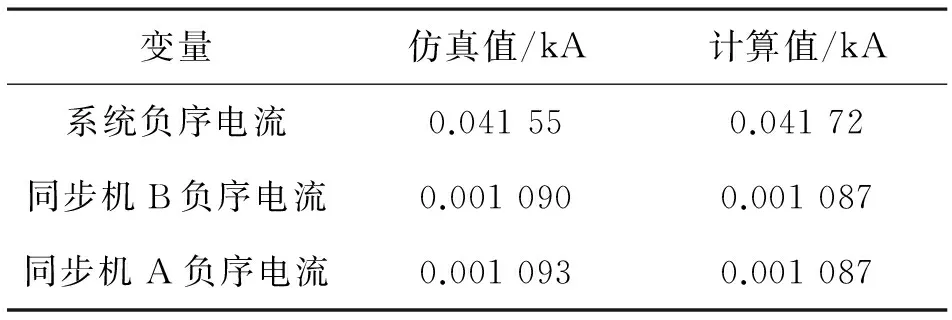
表3 雙同步電機無窮大系統主要變量對比

3.2十三節點配電網系統

為了進一步驗證所提出的不對稱計算方法，并分析直驅風機對近區系統負序電流的影響，建立典型十三節點配電網系統，將直驅風機與同步電機接入，系統結構見圖7，在節點675接入直驅風機，在節點634接入同步電機。系統負載節點主要參數見表4。

其中，節點646、684、611、652、680的額定電壓為0.4 kV，需要經過變壓器并網，變壓器的容量都為10 MVA。為了簡化計算，在具體建模中將變壓器的阻抗設成極小，因而在分析計算中可以忽略。同時，負載節點在建模中用電阻與電感并聯的形式替代，電阻和電感的參數可根據節點的額定電壓和額定功率換算。傳輸線參數ZL1=ZL2=0.034 2+j0.267 0(Ω/km)。

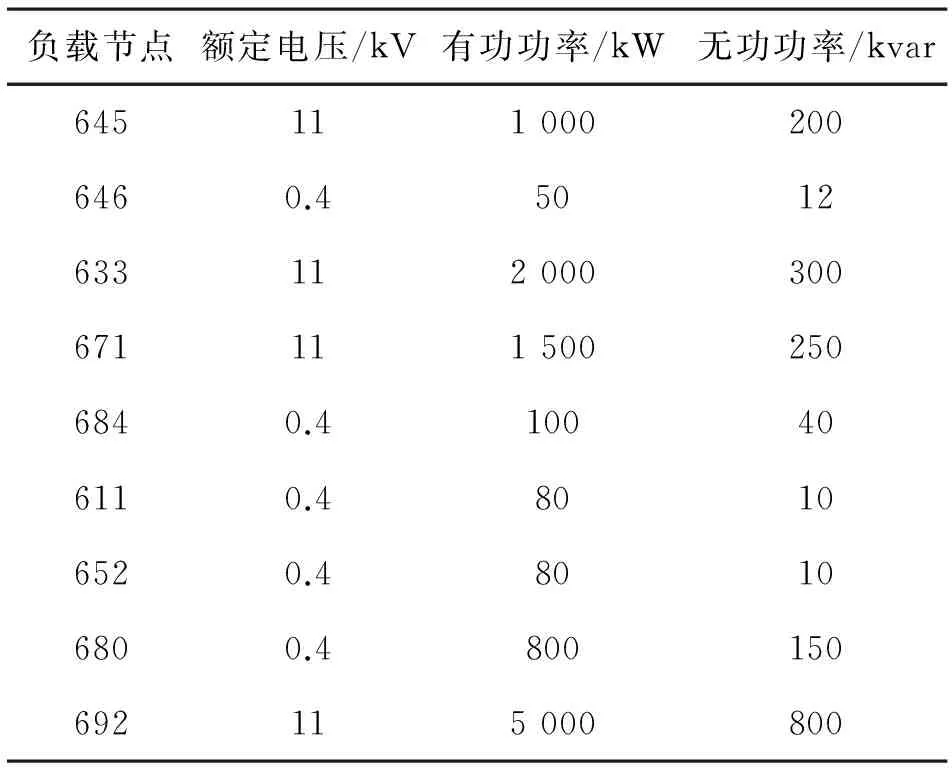
表4 十三節點系統負載節點主要參數

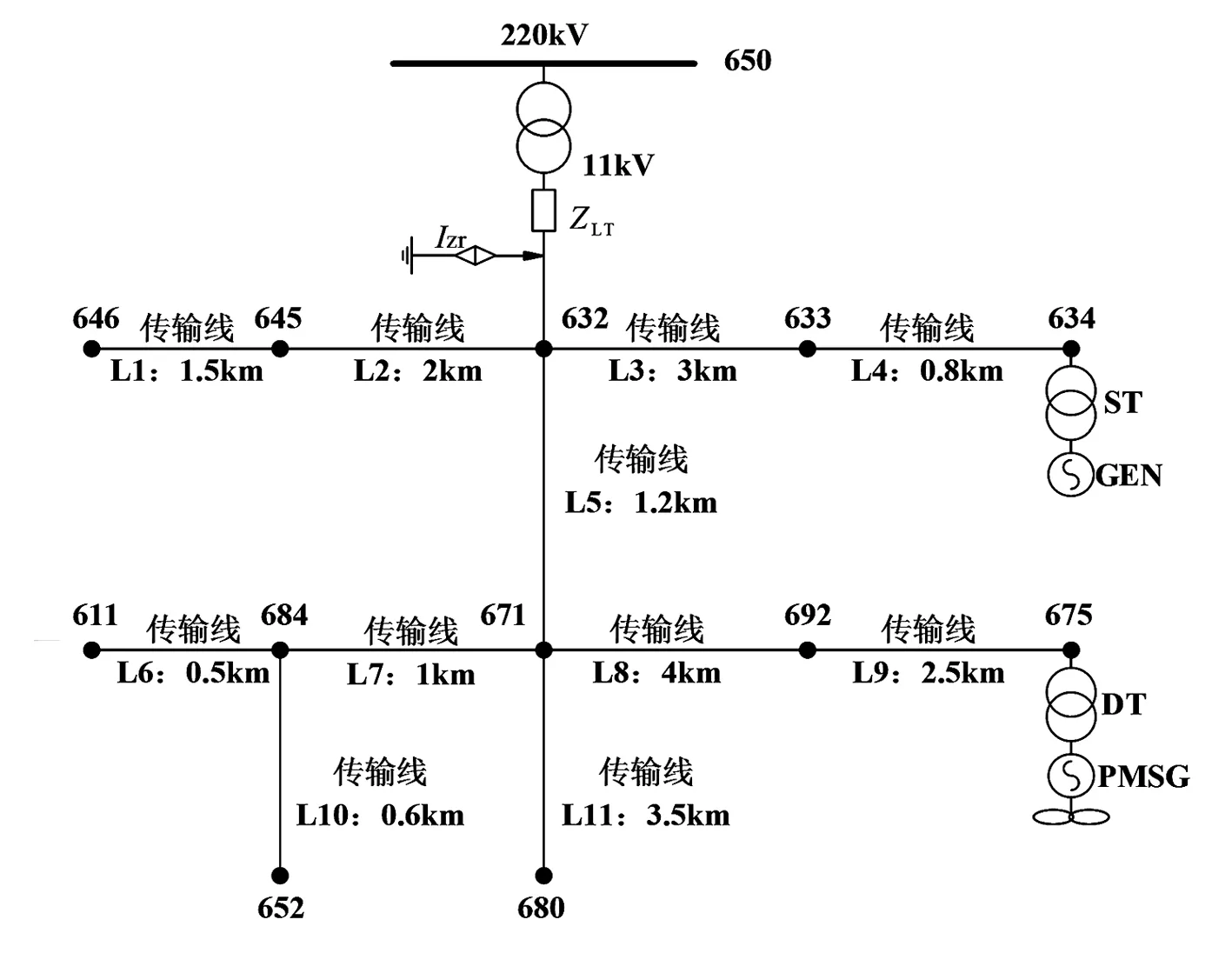
圖7 十三節點配電網系統

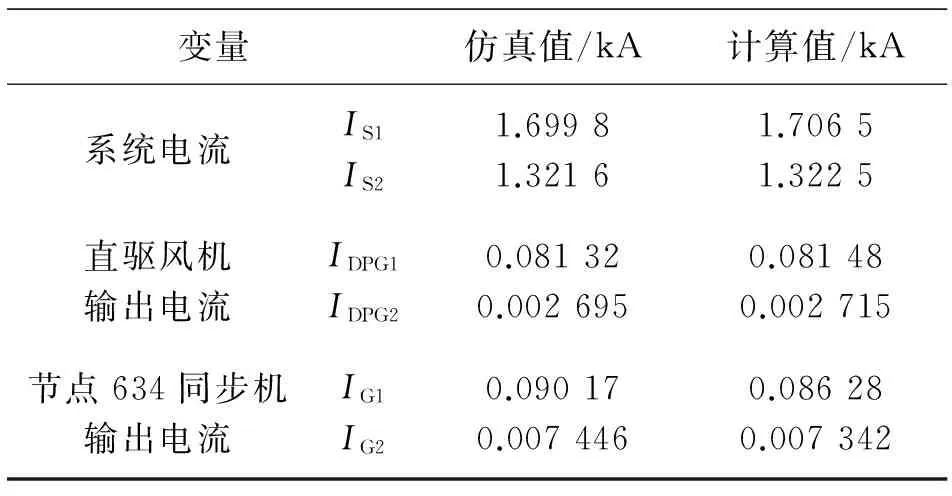
變量仿真值/kA計算值/kA系統電流IS1IS21.69981.32161.70651.3225直驅風機輸出電流IDPG1IDPG20.081320.0026950.081480.002715節點634同步機輸出電流IG1IG20.090170.0074460.086280.007342

表5給出了十三節點系統主要變量理論計算值與仿真值的對比，可以看出仿真值與計算值很接近，證明了計算方法的正確性。

類似地，在同一節點，將直驅風機替換為相同容量的同步電機，系統主要變量的計算與仿真結果如表6所示。表7給出了兩種接入情形下，各負載節點所在支路負序電流的仿真值。

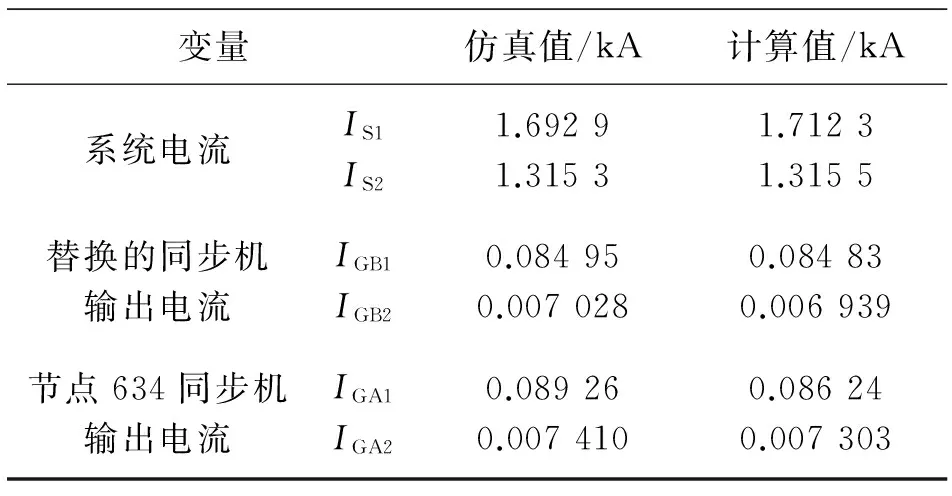
表6 同步電機接入十三節點系統主要變量對比

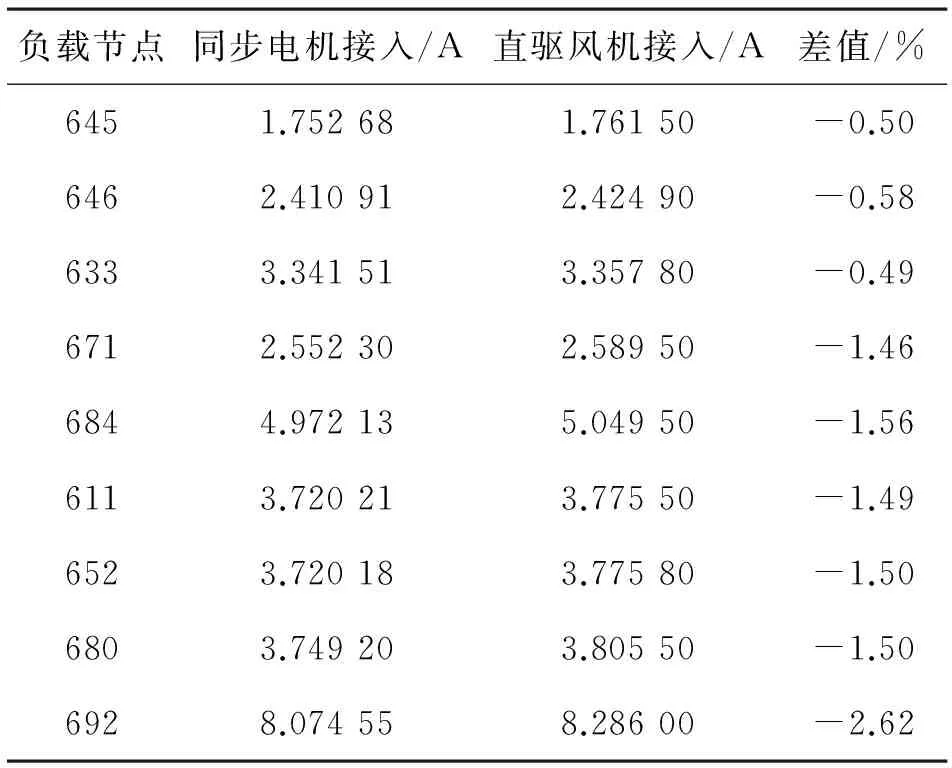
表7 兩種接入情形下負載節點所在支路負序電流對比

對比表5和表6可以看出，直驅風機接入比同步電機接入，使節點634所接同步電機輸出了更大的負序電流。表7表明直驅風機接入時，系統各負載節點所在支路的負序電流更大，驗證了理論分析的正確性。

4 結 論

針對具備不平衡運行控制的直驅風機，分析了負序電流注入下，含直驅風機系統的不對稱計算原理，提出了一種計算系統參數各序分量穩態值的方法。從理論上分析了直驅風機對近區系統負序電流的影響，結果顯示，相比于同步電機，直驅風機使系統其他支路的輸出負序電流更大。在雙機無窮大及十三節點配電網兩個測試算例中，利用MATLAB 的理論計算值與PSCAD的暫態仿真值進行對比，對比結果驗證了所提方法及結論的正確性。

[1] 王長路, 王偉功, 張立勇,等. 中國風電產業發展分析[J].重慶大學學報自然科學版, 2015, 38(1):148-154.

[2] 賀益康, 胡家兵. 雙饋異步風力發電機并網運行中的幾個熱點問題[J].中國電機工程學報, 2012, 32(27):1-15.

[3] Wang Z, Nian H, Hu J. Enhanced Control Strategies of Permanent Magnet Synchronous Wind Power Generation System under Unbalanced Grid Voltage Conditions[C]∥Asia-Pacific Power and Energy Engineering Conference，IEEE, 2010:1-4.

[4] 姚駿, 陳西寅, 廖勇,等. 電網電壓不平衡時永磁直驅風電機組的控制策略[J].電力系統保護與控制, 2011, 39(14):99-106.

[5] 姚駿,陳西寅,廖勇,等. 抑制負序和諧波電流的永磁直驅風電系統并網控制策略[J].電網技術,2011(7):29-35.

[6] Ng C H, Ran L, Bumby J. Unbalanced-grid-fault Ride-through Control for a Wind Turbine Inverter[J].IEEE Transactions on Industry Applications, 2008, 44(3):845-856.

[7] 程航, 曹五順, 周明星. 不對稱電網電壓條件下直驅永磁風力發電機組并網逆變器的雙電流閉環控制策略的研究[J].電力系統保護與控制, 2012, 40(7):66-72.

[8] Baran M E, El-Markaby I. Fault Analysis on Distribution Feeders with Distributed Generators[J]. IEEE Transactions on Power Systems, 2005, 20(4): 1757-1764.

[9] 周念成, 葉玲, 王強鋼, 等. 含負序電流注入的逆變型分布式電源電網不對稱短路計算[J].中國電機工程學報, 2013, 33(36): 41-49.

[10] 孔祥平, 張哲, 尹項根, 等. 含逆變型分布式電源的電網故障電流特性與故障分析方法研究[J].中國電機工程學報, 2013, 33(34): 65-74.

[11] 潘國清,曾德輝,王鋼,等. 含PQ控制逆變型分布式電源的配電網故障分析方法[J].中國電機工程學報,2014,34(4):555-561.

[12] 劉素梅,畢天姝,王曉陽,等. 具有不對稱故障穿越能力逆變型新能源電源故障電流特性[J].電力系統自動化,2016(3):66-73.

[13] 張興,張崇巍. PWM整流器及其控制[M].北京：機械工業出版社, 2012.

A steady-state asymmetric calculation method for power system with direct-driven permanent magnet synchronous generators (DDPMSG) after the injection of negative-sequence current is proposed. In the positive and negative sequence networks, DDPMSG with the control strategy under unbalanced condition could be equivalent to the controlled current source. Then voltage and current equations based on positive and negative sequence networks of power system are listed. The sequence components of parameters of power system could be gained by solving the simultaneous equations combining the voltage and current equations and the current commands equations of the control strategy. The influence of DDPMSG on the negative-sequence currents of the system near DDPMSG is analyzed theoretically. The results show that DDPMSG may increase negative-sequence currents of other branches comparing with the synchronous generator. Finally, two case studies based on two-machine system and 13-node distribution network are presented, and the comparative analyses between theoretical calculations and simulation results verify the correctness of the calculation method and conclusions.

direct-driven generator; negative-sequence current; control strategy for unbalanced condition; synchronous generator

TM614

：A

：1003-6954(2017)04-0014-06

2017-04-06)

徐紅燦(1992)，碩士研究生，研究方向為電力系統穩定與控制、新能源并網等； 王曉茹(1962)，教授、博士生導師，主要研究方向為電力系統穩定性分析與控制、含大規模可再生能源的電力系統的保護與控制等。