水輪發電機失磁保護阻抗特性分析

郭思源，李理，洪權，李輝，劉海峰，蔡昱華，張命強

（1.國網湖南省電力公司電力科學研究院，湖南長沙410007；2.湖南省電網工程公司，湖南衡陽421002)

水輪發電機失磁保護阻抗特性分析

郭思源1，李理1，洪權1，李輝1，劉海峰1，蔡昱華1，張命強2

（1.國網湖南省電力公司電力科學研究院，湖南長沙410007；2.湖南省電網工程公司，湖南衡陽421002)

本文以水輪發電機為研究對象，詳細推導了其靜穩邊界阻抗圓的動作特性。針對具體發電機變壓器組保護裝置的失磁保護判據進行研究，經研究表明投入無功反向判據并不能減小實際運行機組的靜穩邊界圓動作范圍。隨后通過一個算例，將低勵限制曲線從功率平面P－Q轉換到阻抗平面R－X，統一在阻抗平面來說明失磁保護與低勵限制的配合關系。

水輪發電機；失磁保護；無功反向判據；低勵限制

發電機組進相運行是解決電力系統局部電壓偏高無功功率過剩的重要技術手段〔1－2〕。當發電機進相運行時，勵磁系統處于欠勵工作狀態，勵磁電流越小則功角越大，同時更加接近發電機靜穩極限。根據 《發電機組并網安全條件及評價》要求，投入生產運行的發電機組應檢查及校核失磁保護〔3〕的整定范圍和低勵限制〔4〕特性，防止由于發電機組運行參數整定不合理，在進相運行時保護誤動作。

文獻 〔5〕討論了汽輪發電機失磁保護與低勵限制的整定配合關系，重點推導了低勵限制線與失磁保護阻抗圓之間的映射關系；文獻 〔6〕同樣以汽輪發電機為例，經論證后指出發電機低勵限制的整定只需考慮與失磁保護靜穩阻抗圓配合即可，且其靈敏度高于異步阻抗圓；文獻 〔7〕探討了水輪發電機失磁保護與低勵限制的配合問題，考慮了失磁保護定子側靜穩判據的影響，但并未考慮發電機實際運行的有功功率區間。

文中以水輪發電機為研究對象，推導了其靜穩邊界阻抗圓的動作特性〔8〕。以具體發電機變壓器組保護裝置為例〔9〕，研究了其失磁保護判據對失磁保護動作范圍的影響，并通過一個算例將低勵限制曲線從功率平面P-Q轉換到阻抗平面R-X，來說明失磁保護與低勵限制的配合關系。

1 水輪發電機失磁保護阻抗特性

1.1 靜穩邊界阻抗圓

水輪發電機是一種凸極機結構，其氣隙不均勻，旋轉時的空氣阻力較大，比較適合于中速或低速的旋轉場合。由于氣隙不均勻，其直軸同步電抗與交軸同步電抗不相等，即Xd≠Xq。圖1為單機系統簡化圖，表示1臺失磁或低勵的水輪發電機通過外接電抗Xs與無窮大系統并列，其中E為發電機空載電勢，U為機端母線側電壓，發電機輸出的功率分別為P和Q；Us為無窮大系統側母線電壓，進入無窮大系統的有功功率為Ps，無功功率為Qs。

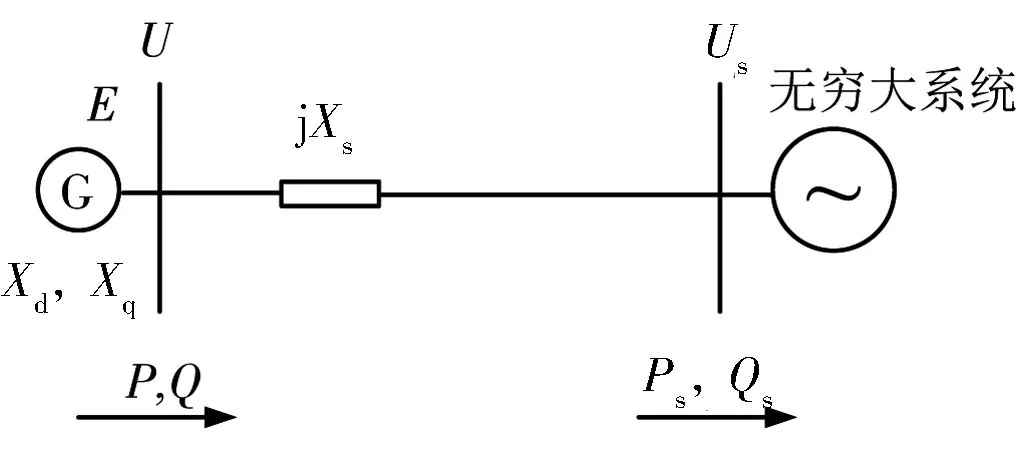
圖1 單機系統簡化圖

依據同步發電機原理，當發電機經jXs與無窮大系統相聯時，輸入系統的有功功率、無功功率分別為:

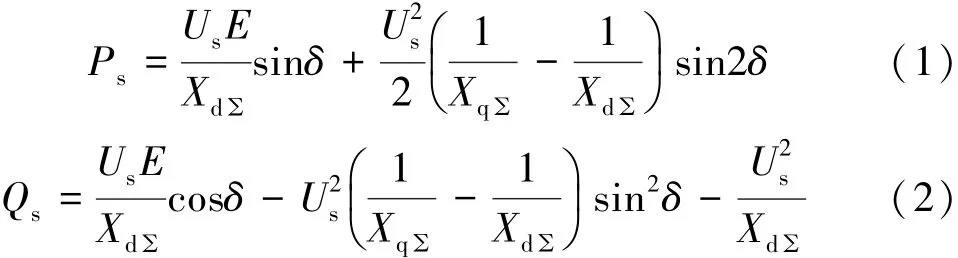
式中 E為發電機空載電勢，δ為功角，XdΣ＝Xd＋Xs，XqΣ＝Xq＋Xs。

對于凸極機，其靜穩極限為dPs/dδ＝0的點，即對式(1)求微分，可得:

其中，

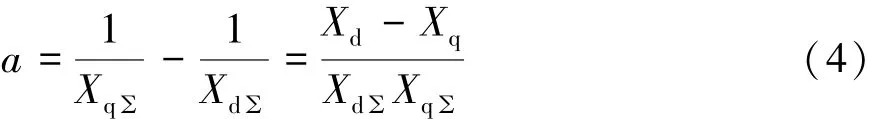
由式(3)可得:

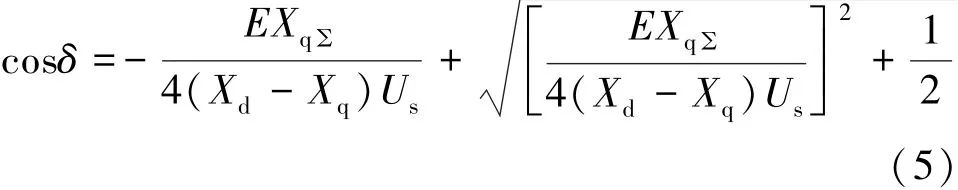
此時的功角δ即為水輪發電機處于靜態穩定極限時的功角。將式(5)代入式(3)，得到:將式(6)代入式(1)和式(2)，即:

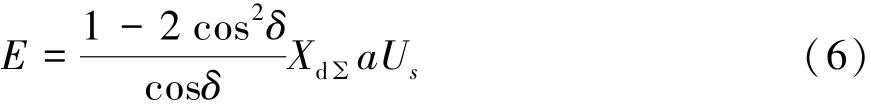
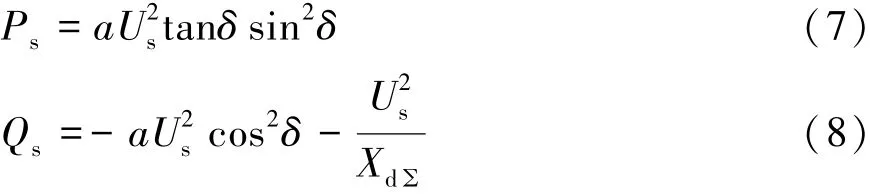
因此，靜穩極限時無窮大母線處的測量導納為:

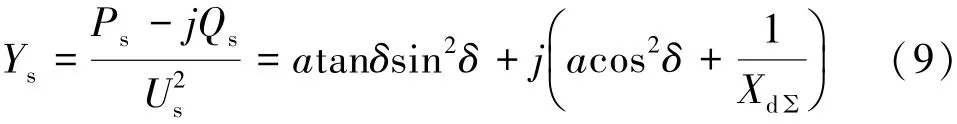
從機端母線側看進去，可得靜穩極限時的機端測量阻抗Z如下:

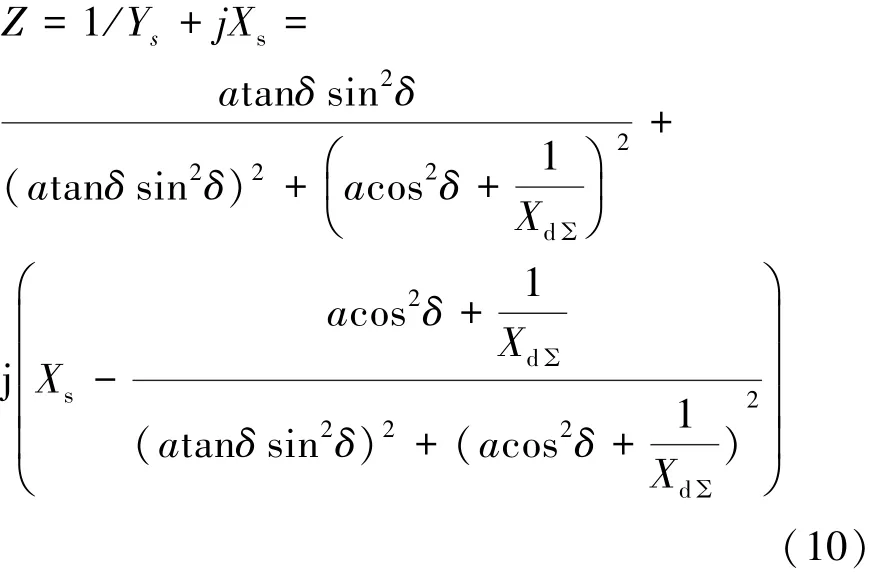
以1臺700 MW機組為例:SN為777.8 MVA，UN為20 kV，PN為700 MW，Xd為0.977，Xq為0.703，Xs為0.327。其靜穩邊界阻抗圓如圖2所示。

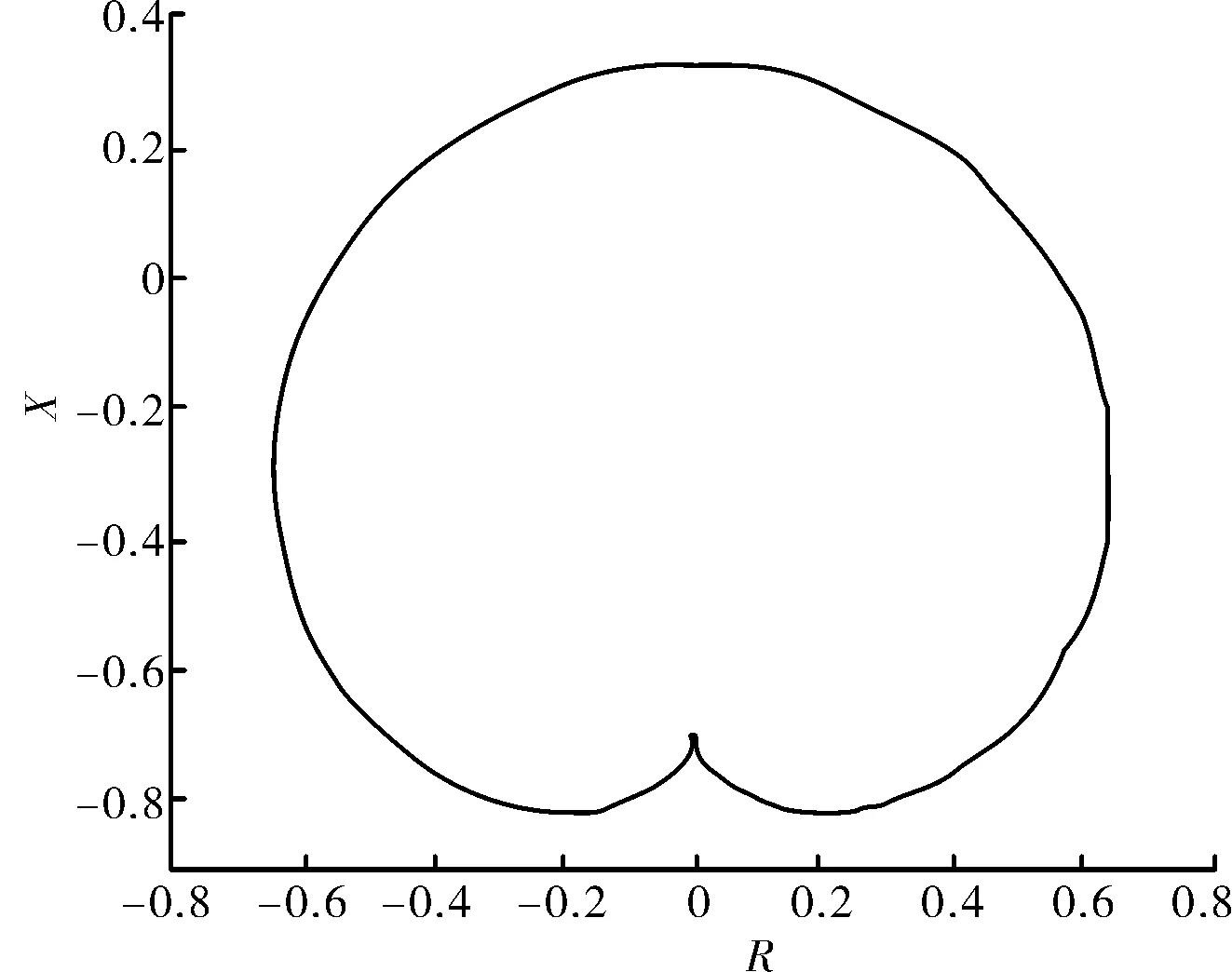
圖2 水輪機靜穩邊界阻抗圓

1.2 無功反向曲線

基于阻抗原理的失磁保護通常以定子阻抗圓作為主判據，輔之以轉子電壓判據、系統低電壓判據、機端低電壓判據和無功判據等輔助判據。根據機組的運行需要，可靈活組合以滿足實際工程要求。

圖3為某公司繼保發變組保護裝置PCS－985B的失磁保護阻抗圓示意圖。其中，Qzd表示無功功率反向定值，圖中虛線為無功反向動作邊界，陰影部分為動作區。根據文獻 〔9〕，當投入無功反向判據Q＜-Qzd與定子阻抗圓判據相結合時，能夠減小失磁保護靜穩阻抗圓的動作范圍。

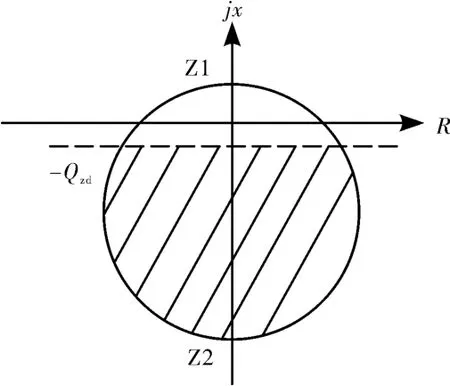
圖3 PCS-985B失磁保護靜穩阻抗圓

然而，失磁保護阻抗圓是在阻抗平面R-X的曲線，而無功反向判據是在功率平面P－Q的一條直線，因此圖3并不是考慮無功反向判據后真實的失磁保護動作區范圍。

仍以該臺700 MW機組為例，假設無功功率反向定值Qzd為0.2，其中有功功率P和無功功率Q均是以發電機額定視在功率為基準的標幺值。根據以下兩式，可將無功功率反向曲線繪制在R－X平面上:

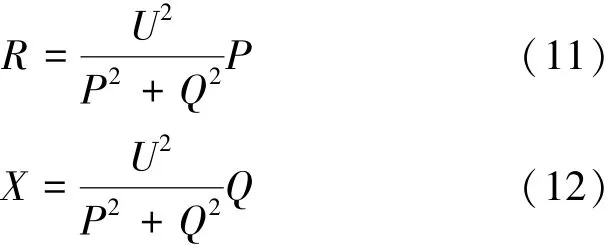
將機端電壓U＝1時的失磁保護靜穩阻抗圓和無功功率反向曲線同時繪制在R－X平面上，分別如圖4和圖5所示。其中，圖4機端電壓U＝1，有功功率0＜P＜1.3；圖5機端電壓U＝1，有功功率－200＜P＜200。

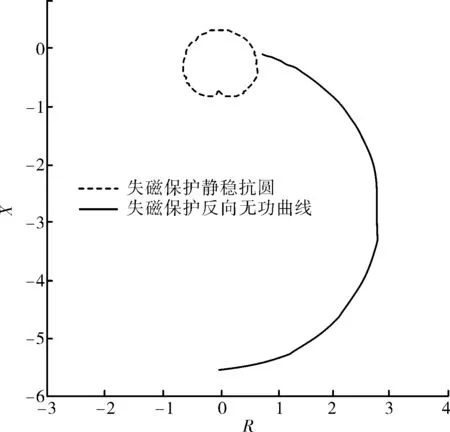
圖4 R-X平面下失磁保護動作特性（0＜P＜1.3)

由圖4可知，當發電機有功功率在0＜P＜1.3之間時，即考慮實際運行機組過載能力工況下的有功運行范圍時，由于P＞0，根據式(11)可得R＞0，因此無功功率反向曲線在R－X平面是在X軸右側的一段圓弧，且距離失磁保護靜穩阻抗圓越近有功功率P越大。此時，無功功率反向曲線并不能切去靜穩阻抗圓的上部，因此并不能減小實際運行機組的靜穩邊界圓動作范圍。

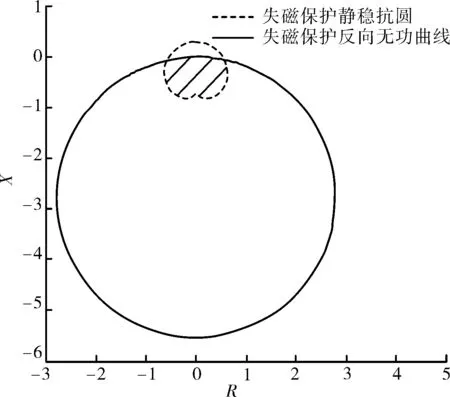
圖5 R－X平面下失磁保護動作特性（－200＜P＜200)

假設有功功率－200＜P＜200，即相對實際運行機組，大幅度擴展發電機有功運行范圍(包括電動機運行方式)，此時無功功率反向曲線在R-X平面是一個圓，并且與失磁保護靜穩阻抗圓有一個交集，如圖5所示的陰影區。因此，理論上講投入無功反向判據能夠減小失磁保護靜穩阻抗圓的動作范圍，但并不是如圖3所示的直線，而是圖5所示的圓弧。如果考慮發電機組實際運行有功功率區間，投入無功反向判據并不能減小靜穩邊界圓動作范圍。

圖6是PCS-985B失磁保護Ⅰ段動作邏輯圖，PCS-985B失磁保護由母線低電壓判據、轉子低電壓判據、定子阻抗判據和無功反向判據4個判據組成。其中，可選擇定子阻抗判據與無功反向判據結合的方式，經與或等邏輯運算出口。由前述推論可知，投入無功反向判據理論上可減小失磁保護靜穩阻抗圓的動作范圍，但對實際運行機組并不能減小其靜穩邊界圓動作范圍，因此可不考慮投入無功反向判據。

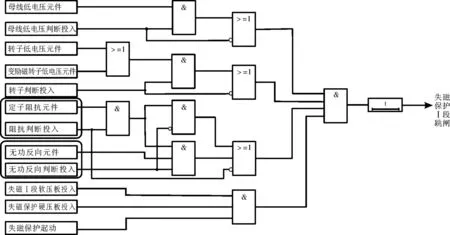
圖6 PCS-985B失磁保護Ⅰ段動作邏輯

2 失磁保護與低勵限制整定配合關系

失磁保護是發電機的保護，低勵限制是勵磁系統的保護。從兩者的構成原理可知，低勵限制可以使機組在進相運行時不超過靜穩極限范圍，而失磁保護在發電機失磁或低勵后及時跳閘保護發電機和系統不受發電機異步運行的危害。因此，兩者在機組進相運行時必須充分考慮配合的關系，即低勵限制在前，失磁保護動作在后。

在功率平面P-Q上，低勵限制曲線應當在發電機實際進相能力的上方，即發生低勵時低勵限制優先動作但不能越過進相能力曲線。本文算例中，機組低勵限制整定曲線換算到機組額定容量下的標幺值表達式見式(13)，為一條直線。

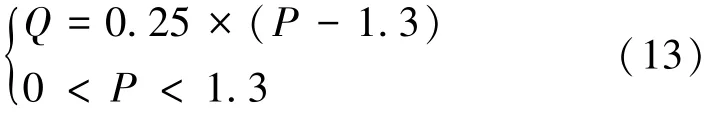
根據式(11)、式(12)將低勵限制曲線(13)轉換到R－X平面，并與失磁保護靜穩阻抗圓、失磁保護無功功率反向曲線繪制在同一張圖中，如圖7所示，其中機端電壓U＝1，有功功率0＜P＜1.3。可見，低勵限制曲線在R－X平面是一段圓弧，在失磁保護靜穩阻抗圓以外。由于靜穩阻抗圓內為保護動作區，因此低勵限制和失磁保護配合關系正確，過渡合理。

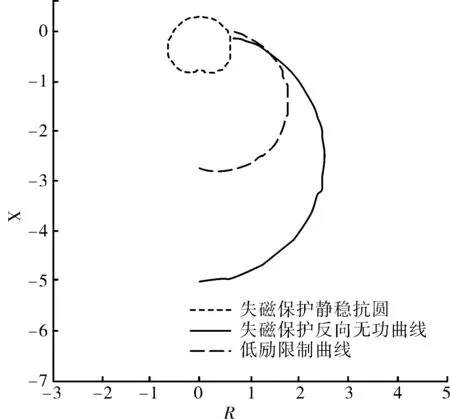
圖7 R-X平面下機組低勵限制與失磁保護動作區關系

圖7 中，對比低勵限制曲線和失磁保護無功功率反向曲線，兩者的類似之處在于均是一段位于失磁保護靜穩阻抗圓以外的圓弧，因此投入無功反向判據與整定低勵限制曲線存在功能上的重疊，作用并不明顯。對于發電機組正常進相運行工況下，只需合理地整定失磁保護靜穩阻抗圓和低勵限制曲線，即可保證失磁保護不誤動作。

3 結論

詳細推導了水輪發電機靜穩邊界阻抗圓的表達式，其形狀為水滴圓。針對某公司繼保發變組保護裝置PCS－985B的失磁保護判據的研究結果表明，投入無功反向判據并不能減小實際運行機組的靜穩邊界圓動作范圍。最后通過一個算例，將低勵限制曲線從功率平面P-Q轉換到阻抗平面R-X，統一在阻抗平面來說明失磁保護與低勵限制的配合關系。

〔1〕王成亮，王宏華.同步發電機進相研究綜述 〔J〕.電力自動化設備，2012，32(11):131-135.

〔2〕嚴偉，陳俊，沈全榮.大型隱極發電機進相運行的探討 〔J〕.電力系統自動化，2007，31(2):94-97.

〔3〕劉一丹，張小易，崔曉祥.火電廠發電機失磁保護阻抗判據的探討 〔J〕.電力系統保護與系統，2010，38(20): 235-237.

〔4〕王偉，石磊，朱曉東.同步發電機低勵限制器實現與應用探討 〔J〕.江蘇電機工程，2009，28(3)；27-31.

〔5〕劉偉良，荀吉輝，薛瑋.發電機失磁保護與低勵限制的整定配合 〔J〕.電力系統自動化，2008，32(18):77-80.

〔6〕郭春平，余振，殷修濤.發電機低勵限制與失磁保護的配合整定計算 〔J〕.中國電機工程學報，2012，32(28): 129-132.

〔7〕李暉，魯功強，王育學，等.大型水輪發電機失磁保護與低勵限制配合問題的探討 〔J〕.電力系統保護與控制，2014，42(5):68-72.

〔8〕王維儉.電氣主設備繼電保護原理與應用 〔M〕.北京:中國電力出版社，2010.

〔9〕南京南瑞繼保電氣有限公司.PCS－985B發電機變壓器組保護裝置說明書 〔Z〕.2013.

Impedance Characteristics Analysis of Excitation-loss Protection for Hydro-generator

GUO Siyuan1，LI Li1，HONG Quan1，LI Hui1，LIU Haifeng1，CAI Yuhua1，ZHANG Mingqiang2
(1.State Grid Hunan Electric Power Corporation Research Institute，Changsha 410007，China；2.Hunan Power Grid Engineering Company，Hengyang 421002，China)

The hydro-generator being study subject，this paper deduces the action characteristics of the static stability boundary impedance circle in detail.For specific excitation-loss protection criterion of generator transformer protection group，the research shows that putting into reactive reverse criterion does not reduce the static stability boundary circle range of the actual operation generator.Then through an example，by converting the low excitation limit curve from the power plane P-Q to impedance plane R-X，the cooperate relationship between excitation-loss protection and low excitation limit is illustrated in the impedance plane uniformly.

hydro-generator；excitation－loss protection；reactive reverse criterion；low excitation limit

TM77

A

1008-0198(2017)04-0004-04

郭思源(1986)，男，博士，工程師，主要從事發電機勵磁控制系統、高壓直流輸電自動控制技術研究。

10.3969/j.issn.1008-0198.2017.04.002

2016-12-13 改回日期:2017-03-30

李理(1987)，男，碩士，工程師，主要從事發電機勵磁控制系統技術研究。

洪權(1987)，男，碩士，工程師，主要從事電力系統運行與控制研究。