基于深度學習的航空器異常飛行狀態識別

吳 奇 儲銀雪 /

(上海交通大學，上海 200240)

基于深度學習的航空器異常飛行狀態識別

吳 奇 儲銀雪 /

(上海交通大學，上海 200240)

飛行設備快速存取記錄儀(Quick Access Recorder, 以下簡稱QAR)保留了原始航班各類重要飛行參數在內的航行信息，使研究分析航空器實時狀況和保障飛行質量成為可能。針對QAR數據高維大樣本的特點，在如今大數據背景下，除了傳統機理建模分析航空器飛行狀態外，采用深度學習的方式建立基于數據驅動的航空器飛行狀態識別模型，理論與實用意義兼具。通過對真實QAR飛行數據的研究，開發了基于深度稀疏受限玻爾茲曼機的異常飛行狀態識別程序。首先利用小波降噪技術對原始飛行數據進行預處理清洗，在一系列典型飛行參數上提取經典時域特征以及小波奇異熵等信息熵特征構成特征集。在此基礎上，分別利用經典的線性主元分析技術和深度稀疏玻爾茲曼機對特征集進行有效降維，最后采用四折交叉驗證方式，通過高斯過程分類器實現對飛行狀態的辨識。實驗結果顯示，基于深度受限玻爾茲曼機-高斯過程分類的飛行狀態識別具有較高分類準確性。

飛行狀態識別；深度學習；高斯過程

0 引言

1903年，飛機的問世，為人類開辟了陸地、海洋之外的新邊疆。由此衍生出來的各類航空器除了作為交通工具極大便利了人們的出行外，還發揮了軍用、民用、商用等諸多用途。航空器大規模寬領域的普及應用，隨之而來的最重要問題便是安全，其中最關鍵的考量當屬如何確保航空器飛行狀態安全可控(新近事故如2014年3月馬航MH370客機失聯，至今仍是未解之謎)。為此，分析和研究航空器飛行狀況的辨認意義重大：不僅是航空器飛行狀態分析的必要基礎，更能為繁忙空域多機(群)任務調度與目標規劃、智能故障診斷和維修維護等安全監控，以及航空器設計優化與成本控制等方面提供重要有效的參考信息。

可行性上，航空器飛行狀態的識別目前大體有三種路徑：基于分解重構的機理建模，其辨識效果與模型準確性嚴格正相關；基于知識經驗庫的專家系統，即便綜合主客觀分析，其不足在于領域專業性與人為主觀判定的局限性；本課題采用第三種路徑，即基于數據驅動的信號處理方法，運用真實飛行數據進行機器自學習，進而捕捉挖掘樣本數據內在特征與飛行狀態之間的關聯，兼具理論與實用意義。

首先在理論研究價值上，研究大數據云計算背景下基于數據挖掘驅動的航空器飛行狀態識別，將打破傳統機理建模和經驗知識結合主觀判定分析飛行事件的套路，有助于建立并完善著眼全流程各環節的飛行數據分析與結果導向型飛行安全控制融合的研究體系。另一方面，也將助推理論研究從事后故障診斷研究向超前預防型預警風控研究發展，從而更有效確保航空器飛行狀態的安全可控。

其次在應用層面，通過深挖捕捉海量飛行數據樣本潛在的特征因子，進而用于識別飛行過程的異常狀態，預防或減少環境因子或人為因子導致的不安全隱患，等效達到了安全保障層前置和有效風險防范的目標；進一步，基于真實飛行數據在線分析平臺的狀況評估體系，呈現了航空器包括氣候狀況、飛行姿態等多維度全方位的情形再現，進一步可用于地面實時快速掌握航空器飛行狀態，并在必要時為空中機組提供有力支援，從而最大限度地減少可能發生的損失。

1 國內外研究現狀

國內外關于航空器飛行狀態的研究，大體可劃分為兩大經典模式：一是借由濾波分析模型遞推計算出航空器運動學方程；二是示教訓練方式，經由對歷史航班相關特征參數信息的訓練學習，形成空管領域的專家經驗[1]。

1.1 國外飛行狀態識別研究現狀

國外的研究在濾波模型和機器學習兩方面均有涉足。Inseok Hwang等人基于濾波模型設計混合模型預測航空器飛行狀態，采用卡爾曼濾波減小了因錯誤預測引入的誤差，進而更有效地捕捉了短時飛行特征[2]。Neogi等人使用隱馬爾科夫模型研究航空器飛行狀態的變化，結合隨機混合系統探測飛行狀態的變化，考慮 了隨機擾動的影響[3-4]。還有學者采用Swarm模型，引入人工智能模擬類似動物的群體效應，用以形成沖突解脫方案[5-6]。2012年，WANG Qing等人基于QAR(Quick Accesses Recorder)數據，提出了EKF-MBF(the Extended Kalman Filterassociated with Modified Bryson-Fraziersmoother)混合算法，改善了相關估計指標精度[7]。C. EdwardLana等人則采用QAR數據分析了高緯度機場降落時的飛行特征，為潛在安全問題提供分析幫助[8]。B.Jia等人引入BF-PSO(Bacterial Foraging-Particle Swarm Optimization)算法來優化KFCM的參數已達到辨識動態與靜態模式下的飛行狀態[9]。

1.2 國內飛行狀態識別研究現狀

國內學者則主要在濾波分析模型聚焦較多且通常結合了空管的專家經驗[10]。張友民等學者為估計高維航空器姿態，采取了非線性濾波模型[11]。耿建中等為確保準確可靠辨識航空器狀況的同時降低運行成本，引入了無跡卡爾曼濾波(Unscented Kalman Filterm)的濾波方法。高原等專門針對飛行狀況規則辨認與提取的課題，以典型參數為研究對象，提出新型量子遺傳算法以期組合尋優，歸納了飛行狀況識別的所謂產生式法則[12]。2013年，王潔寧等將終端區數據一致化，并利用歷史航行信息特征訓練隱馬爾科夫模型，搭建了時序辨認模型[13]。2015年，李軍亮等人預先將對待識別的飛行狀態經由Elman網絡預先分類，在某款直升機的辨識應用中取得成功[14]。2016年，熊邦書等人提出基于支持向量機(Support Vector Machine,SVM)的直升機飛行狀態辨認方法，在數據集較少情況下明顯提升了分類正確率[15]。趙元棣、孫禾為準確高效預測航空器飛行狀態，提出了HMM-BP混合模型，通過HMM模型對航空器進行時序建模，再利用BP神經網絡對航空器飛行狀態進行推理預測，計算快效率高[16]。谷潤平等選用新型數據融合算法和擴展卡爾曼濾波算法分析飛行參數，提高了判別預測的準確度[17]。

2 特征提取技術

航空器飛行狀態的識別，是一類典型的模式識別問題，核心在于透過元始一般性的數據信號，發掘其內在獨特的關聯，從而將一般的飛行信號轉化為可識別的有特征信號。在完成前述對一手數據降噪處理后，緊接著的難題便是對特征的表示與提取，試圖將原先隸屬于相異類別的典型參數進行提取后轉化為或有物理解釋意義或有識別意義的數據，更好地強化表征航空器所處的狀況。特征工程的方式層出不窮，經典手段諸如均值、方差和均方根，在展示信號(也適用時間序列)的幅值特征及不同類別參數的差異性，已由早期統計學應用推廣到各類數據分析領域。然而，僅僅使用傳統時域的特征分析技術已無法為高維度強耦合的繁雜飛行數據分析提供強有力支撐，難以準確應對非線性或非平穩的信號特征。為滿足人們對更高識別準確率的迫切現實需求，發展運用新的特征提取技術是一大廣闊的舞臺。本節除簡介經典時域內特征提取技術外，還將熵量特征融合信號變換技術創新特征工程，引入自回歸滑動平均系數熵(ARMAE)及小波奇異熵(WSE)，以構建更精確反映原始數據潛在關聯的特征集。

2.1 時域特征提取技術

特征是任何學習型算法的原材料。本小節引入三個常用的時域的統計特征量：均值(mean)、方差(variance/deviation)、均方根值(RMS, root means quare)。

對于時間序列進行一維數據分析時，均值是最常用以描述飛行數據的特征量。這里均值不是幾何平均值，指的是算數平均值，計算方法見式(1)(xi為樣本內數據值，Pxi為xi出現的幾率),常用以表征原始波形的幅值特征。若將原始信號視作不同頻率信號之疊加，此時，均值的物理意義表現為信號中直流分量的大小。

進一步，為了反映原始全體單個樣本與均值的關系(離散程度)，引入方差(用variance或deviation表示)，計算方法見式(2)(其中，xi為樣本內數據值，Pxi為xi出現的幾率)。由公式易知，方差是一個離差量，描述的是時間序列的波動范圍，而且是基于均值的分散特征：計算時扣除了均值這一表征直流分量的參考基準，故方差大小又表征了信號交流分量的強弱，也即交流信號的平均功率。

融合考慮交直流分量的功率，我們還可以引進均方根值，用RMS(Root Mean Square)表示，計算公式見(3)，也稱有效值。均方根的平方即均方值，物理意義為信號的平均功率，這里的平均功率即信號的直流分量功率與交流分量功率之和。

2.2 自回歸滑動平均熵

本小節從時域內的自回歸滑動平均模型出發，引入熵概念，定義自回歸滑動平均熵，用以衡量反映飛行數據的信息量及體現原始信號在時間維度上的隨機不確定性。

從理論視角來看，自回歸滑動平均模型(Auto-Regressiveand Moving Average Model, 簡稱ARMA)集自回歸模型(AR)和滑動平均模型(MA)之大成，是以待定系數標準模型應對隨機過程的經典手段：將輸入信號視為隨機變量，從而，信號在時間維度上的延展反映為隨機變量所具有的依存關系。該模型是差分多項式混合模型，綜合考慮受因素演化的聯動影響效應和自身變動規律的影響效應，可用于消除序列的線性依賴從而去除序列的自相關性；同時也是長期追蹤歷史資料并加以回歸預測的利器，如可用于國家或省級內城鄉居民的收入差距預測的研究、用于市場規模及銷量預測的零售消費業研究，等等。

我們在自動控制原理里學習過，一個零均值的平穩序列，其在外界激勵下的響應(在t時刻記為Xt)不僅與當前和過往的響應值相關，還與激勵前外在的擾動值密切聯系，滿足這樣規律的可稱之為自回歸移動平均系統。在數學意義上建模即稱樣本集在時間維度上服從(p,q)階自回歸滑動平均混合模型，記為ARMA(p,q)：

其中，{at}為白噪聲序列。特別地，p=0時模型退化為MA(q)；q=0時模型即為AR(p)。

由上述公式易知：定階，即確定上述p,q值，是搭建自回歸滑動平均模型成功與否的關鍵。基本思想容易理解，通過逐步增加p,q值直到階數增加而殘差平方和無法明顯下降為止。本文采用先預估(p,q)范圍，而后通過模型擬合度量AIC極小準則來定階。AIC[18]計算公式如(5)所示，V為模型殘差方差，N為序列的長度。

經由上述步驟，ARMA模型參數業已確定，容易發現，應用于高維的飛行參數數據集時，各參數在時間維度上適用的ARMA模型系數的長度不同，不便于后續特征處理；同時，儀表盤參數在時間維度上呈現出的復雜性某種意義上可用隨機程度加以描述，因為序列增長隨之衍生出新序列，這種模式的演化正是系統復雜性的反映。能否考慮變化混亂度的因素呢？很幸運，可以用德國熱力學家R.Clausius提出的熵(Entropy)評價。回溯科學發展史，熵概念的問世，不僅標志著衡量系統復雜度的全新思路誕生，更是有廣闊里程碑意義的：早已延拓至熱力學外的信息學、數理應用和生命科學等領域。譬如，1948年Shannon第一次給出信息模型的信息熵，定量地解讀了信息這個抽象的觀點。本文使用的自回歸滑動平均熵(Auto Regressive Moving Average Entropy, ARMAE)源自于自回歸滑動平均模型[19]，計算方式如下：

如此一來，借由通信原理的信息熵的思路：信息量大小反映于基本信息符號重復出現頻次的概率，結合消除序列自相關性的自回歸滑動平均模型，定義的體現飛行參數隨機不確定性的復合熵量ARMAE，將為后續的飛行狀態識別提供更堅實可靠的保障。

2.3 小波奇異熵

前述的特征提取著眼于人們日常習慣的時域，然而，頻域分析是上世紀以來信號分析更為主流的分析方法，如傅里葉變換。不過，該方法也幾乎全然摒棄了時域的信息。于是，由傅里葉分析衍生進化出的小波分析，成為了具備優良時頻局部化性能的時-頻分析新方法。本小節將描述序列混亂度的奇異熵集成小波分析思想，引入小波奇異熵(Wavelet Singular Entropy, 簡稱WSE)刻畫非線性強噪聲奇異能量分散的統計特征，以綜合更多動態特征提高對噪聲的免疫力及狀態識別的準確率。

小波變換的原理方法已在2.1節提及，此處不做贅述。降噪飛行數據經小波變換后再經由內積公式即可得到小波系數陣A，從而在多頻率多尺度下分解原始信息為主要逼近分量和細節微調分量，等效于反復組合運用高低通濾波器，兼備了單一時域或頻域分析法的優勢。

數學的美在于簡潔，時頻的直觀分布還不夠，大數據量屬性是準確進行模式識別的掣肘。線性代數中的奇異值分解理論，能將秩為k的任何階次的矩陣A按奇異值分解為k個單秩子陣的加總(詳見公式(8))，達到特征值對角化呈現之效用，這樣一來，奇異對角陣實質上表征了待分解陣A的最小模態特征。

其中，U、VT均為正交矩陣，Λ上對角元素λi(i=1,2,…,r)即為A陣的奇異特征值。

小波系數陣A通過SVD[24]分解后所得的對角陣，簡潔地刻畫了飛行數據的時頻分布特性。為進一步度量分布的混亂程度，結合2.2節的介紹，將奇異特征值用熵進行表示。奇異熵事實上是一種信息熵。我們知道，香農信息熵理論奠定了通信原理的基石。通俗地借由生物學概念不難理解，在基本信息要素構成的生態系統中，基本信息越多越難以加以定性，因為其出現的頻次不會完全一致，即出現了混亂隨機性；由此出發，以概率視角刻畫這種隨機不確定性便十分自然了：考慮小波變換后系數陣A的奇異值，依信息熵原理計量得小波奇異熵如下，參數k表示非零特征值的數目。

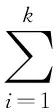
綜上，小波奇異熵的計算過程如圖1所示。

3 深度稀疏受限玻爾茲曼機網絡

3.1 深度置信網絡

與傳統(以主元分析為經典)樣本數據特征分析程式相比，深度置信網絡是個概率發生器，不具備一般人工特征提取時不可避免的主觀不確定性，降低了對專家系統或稱經驗知識的密切依賴從而具備自動提取信號特征的自適應性；此外，該模型非常適合非線性非低維的飛行數據處理，這在后續的實驗驗證中可以得到完美體現。DBN模型由單層反向傳播網絡(BP，Back-propagation)和幾層限制玻爾茲曼機(RBM)構成[25]，結構如圖2所示。

深度置信網絡的模型搭建過程主要分為兩大塊：其一是訓練若干層的RBM，采用無監督的方式，從而保證特征向量向其他空間投射時仍能保留盡可能多的能量[25]；其二就是有監督地借由頂層的反向傳播網絡訓練優化網絡全局，從而微調網絡模型以獲取深度置信網絡的最優參數。

由上面的介紹，不難獲知：受限玻爾茲曼機(RBM)是DBN中的關鍵基本環節。作為玻爾茲曼機的一種特殊形式[26]，受限玻爾茲曼機由可視層和隱含層構成，底層靠n個可視節點排列而成，頂層由m個不可見節點堆成故稱為隱含層并用以提取特征。受限玻爾茲曼機的網絡結構可用圖3展示。

定義受限玻爾茲曼機的網絡能量可用下式：

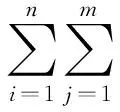
其中，b=(b1,b2,…,bn)表征的是底層可視節點的轉移量，c=(c1,c2,…,cm)表示隱含層的隱藏節點偏移量，wn×m則是溝通隱含節點與可視節點的權重矩陣。

采用概率發生的方式有效防止了人為主觀臆斷。受限玻爾茲曼機網絡實質上是幾率模型：對于輸入數據v=(v1,v2,…,vn)，RBM網絡充當了中繼處理再生器，輸出對應的隱含特征向量h=(h1,h2,…,hm)，從而使得聯合概率p(v,h)極大化。其中，p(v,h)滿足式(13)。

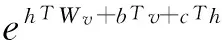
進一步詳解：可視意即一個觀察入口，從已知的底層可視節點獲取隱含層的節點值，有公式(14)作為橋梁；為達到不斷優化不斷微調，沒有反饋不行，即上述的逆向操作也需要可行：由已知的頂層節點亦可獲取底層可視節點的值，公式見(15)。

如前所述，深度置信網絡是將若干層受限玻爾茲曼機預訓練的模型結合反向傳播網絡監督下進行微調的網絡模型，從而提高全模型的計算性能。以下將整套模型的實施步驟分為預訓練環節和微調環節敘述。

首先，預訓練環節指的是無監督式地自下而上的采用若干層RBM自訓練方法獲取穩定的網絡結構。這一模型參數的獲取可借由極大化RBM網絡訓練集的對數似然函數獲取，見式(16)。

對訓練樣本運用Gibbs采樣，可有下面的對數似然的梯度近似表達式。

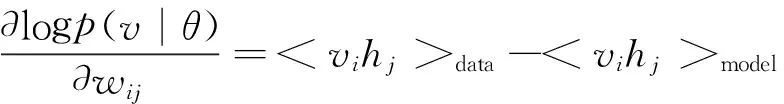
不過針對飛行數據這樣的高維數據時，Gibbs采樣次數過多使得整個訓練過程效率難以接受，需要保證計算精度的情況下提高計算速度。Hinton于2002年創立的對比散度(Contrastive Divergence, CD)是一種快速學習方法：通過CD法僅需k步(通常情況下僅需一步)，下面展示了其參數的更新公式。

其中，ε是學習速率，<>recon為樣本分布的期望。

現在介紹微調階段。作為一個有監督的分類器，反向傳播網絡(BP)在整套深度置信網絡中起著微調全體結構從而達到全局最優的作用。這一細調過程依靠的是誤差信號的逆傳播以調整若干層前饋環節。訓練數據逐層傳播到頂層獲取輸出過程中，每個神經元均有一個激活函數，通常為非線性的sigmoid函數：

其中，xi稱為神經元i的激活值，yi即為輸出。

將網絡輸出值與標準值作差即得誤差信號，再將這一反饋信號從輸出層向輸入層逐層傳播以對網絡參數尋優即可。

3.2 稀疏受限玻爾茲曼機

生物醫學的臨床研究成果啟發我們：人腦處置信息的過程并不是滿倉全負荷行為，通常僅少數的神經元被激發。這一規律被稱為稀疏編碼的算法用以模擬大腦編碼歷程[27]。那么，仍然從概率視角，限制整套網絡的激活概率能否提高網絡對噪聲干擾的魯棒性呢？經過稀疏受限玻爾茲曼機(SRBM)即可。

需要首先說明的是，由于本文實驗測試采用的是真實飛行數據，可視層輸入必須是真實數據不是布爾型二值數據，故應建立高斯受限玻爾茲曼機模型[28]，此時確定狀態下RBM網絡的能量定義為：

上式中的參量與前面RBM能量式的定義相同，σ在實際應用中設定為1較常見[28]。以此類推，我們仍然可以搭建可見層節點與隱含層節點的橋梁：

此時，數值上，隱含節點表現為稀疏性，故而還得在目標函數上疊加一個正則化項以確保隱含節點數值維持低激活率。具體說來，對于擁有m個樣本的數組{v(1),…,v(m)}，優化目標見式子(27)。

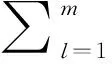
其中，λ表示正則化常數，隱含節點的稀疏性由稀疏常數p把關控制。

這樣一來，經過預訓練過程后，得到的便是SRBM參數的值，再通過類似標準深度置信網絡模型的微調技術手段，便可有效獲取SRBM模型的最優參數，從而學習到不同類別的特征差異。下一部分，將結合實際應用展示SRBM的強大功能。

4 基于高斯過程的飛行狀態識別

定義一個二分類問題，首先訓練集{(xi,yi)|i=1,…,m}，xi為輸入向量，X=[x1,…,xm]T，yi∈{-1,+1}，yi表示兩種輸出標簽的類別。已知訓練集，則測試集x*屬于+1類的概率可表示為：

其中σ(z)=1/(1+e^(-z))，易知此函數范圍為(0,1)；一般當π(x)>0.5，可認為測試樣本x*屬于+1類，否則應劃分至另一類。當測試樣本x*為待預測樣本時，預測一般分兩步：計算f(x*)的分布及其概率預測值：

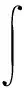
以上兩式計算前提在于似然函數是高斯函數，也就要求在回歸情況下方可行。當分類問題中，似然函數并非高斯函數，上述兩式不能精確計算，只能近似這兩個積分，這時我們可用高斯分布近似f*的后驗分布：

上式的均值、方差如下(式中，k*=[k(x*,x*),…,k(xm,x*)T為測試集的數據與訓練集的數據的協方差)

這樣一來，便可用近似解分析非高斯分布以最佳近似高斯分布，即對于測試集而言，其高斯預測概率值的解可表示為：

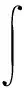
至此我們基本闡釋了高斯過程分類的基本原理，下一小節希望將其應用到前述降維后的典型飛行參數的特征集中，以完成航空器飛行狀態模型的建立與測試。

5 實驗

5.1 實驗數據

自1997年起，中國民航總局(CAAC)依據中國民航適航指令要求所有國內運輸類飛機強制安裝飛行設備記錄儀器(Quick Access Recorder,簡稱QAR)。也正是因為QAR記錄著航班包括飛行位置、操作控制等諸多性能方面的信息，分析研究QAR數據將有助于提高飛行安全和監測飛行品質。然而對于各大航空運輸公司而言，QAR飛行數據屬于核心商業機密，故無論國內還是國外，基于QAR飛行數據的研究相對較少。本論文實驗數據源于國家級基金項目，實驗數據為真實飛行數據，是同一家航空公司同一機型(波音747)的同一航線(浦東-白云)的兩次不同天氣狀況(能見度差異較大)的QAR飛行數據。選取的飛行任務為飛行中最危險也即事故發生率最高的進近著陸階段[20]，每組數據共3 000個樣本點。驗證平臺選取64位Windows10操作系統，并利用編程軟件MatlabR2014a搭建實驗環境，如圖4所示。

考慮到最終搭建的飛行狀態識別不僅限于分析還要能進一步用于實時惡劣狀態預警，因此模型判斷時間應盡可能縮短，故本文選取最能反映航空器飛行姿態的典型飛行參數[21]進行特征提取并建模，初始的典型飛參集列表詳見表1。接下來，本文將運用數據挖掘即機器學習的手段通過QAR數據搭建航空器飛行狀態的識別流程。

5.2 典型飛參特征集的降維

5.2.1主元分析線性降維

在5.1節我們完成了面向典型飛參的特征集構建，本小節中我們利用本文前述的理論知識，將主元分析法應用于典型飛參特征集的降維。如前所述，PCA主要流程為將中心化后的樣本求取其協方差，獲得降維矩陣后映射即得降維數據。這里，我們為了直觀展示降維后效果，利用主元分析將5.1節中得到的包含時域、ARMAE、WSE特征在內的120×72維典型飛參特征集(兩種天氣狀態下共計120組，每組72維特征)，降維到3維空間使其可視化。

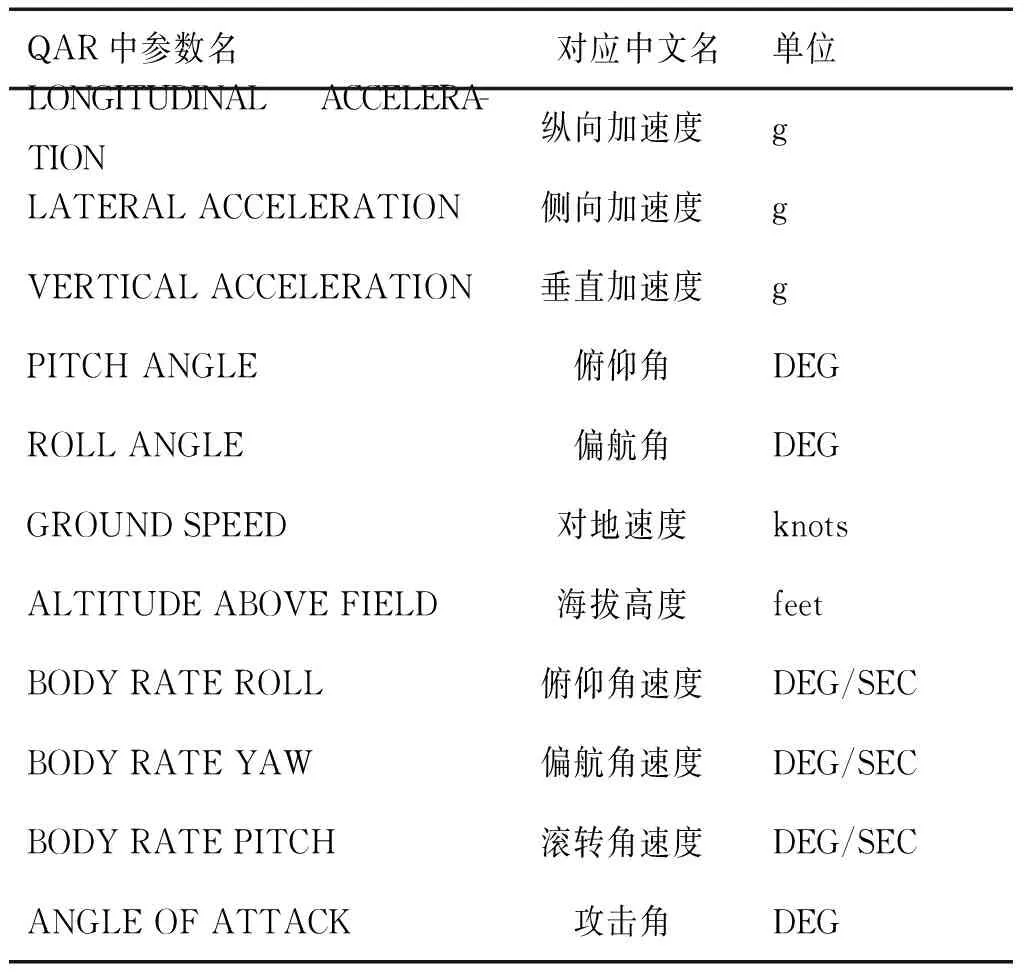
表1 建模所選取的典型飛行參數集

由圖5可見，對于典型飛行參數特征集通過PCA降至3維后，其特征點散落在三維空間各處；兩種相異天氣狀態類別的特征點互相交織，很多無法劃分。由于PCA是線性降維算法，雖對于原始信號一定程度上保留了更多能量卻無法提取非線性的重要特征。為此，我們接下來看看非線性數據降維算法SRBM處理的效果。

5.2.2稀疏受限玻爾茲曼機降維

如前所述，QAR數據屬于各大航空公司的商業數據，由于數據來源的限制，無法獲取非常多的樣本訓練模型，因此除了需要盡量減小噪聲對模型的干擾影響，還需要防止模型學習中容易發生的過擬合情況。本文前面幾節專門敘述了SRBM在這方面的強大優勢：透過限制玻爾茲曼機(RBM)模型正則化隱含層里的隱藏點，便可有效對隱藏點概率加以限制從而達到稀疏的目的。下面將運用SRBM算法對5.1節得到的典型飛參特征集作降維。由于QAR記錄的參數是真實的航行狀態，故不必對真實數據作二值化的脫敏處理，但要在降維前對典型飛參特征集的樣本作規范化處理。

所謂歸一化，即將待處理數據限制在擬定的范圍內，比如將樣本特征歸一化到[0,1]間，表征其在統計意義上的概率分布。這樣做的好處在于，一方面便于后續數據處理使本不具備可比性的數據具備相對可比性，同時由于是等比例縮放，也保留了原數據間相對大小關系；另一方面當然也提升算法收斂速度以更好滿足實時要求，因為這樣處理避免了數值計算中的復雜度。本節采用的歸一化包含樣本中心化和去量綱處理兩步(需要說明的是，Matlab中僅使用自帶normalize函數即可完成歸一化操作)。

首先是數值中心化，即使數據集的均值歸零以便于后續降維算法處理：

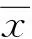
第二步便是去量綱，即將數據的方差切換為1，公式如下：

與PCA降維輸入的樣本數據相同，我們已提取時域、ARMAE、WSE等特征在內的典型飛參特征集，共計正常天氣狀態60×72維特征集數據、異常天氣狀態60×72維特征集數據。完成前述歸一化操作后，第二步就是設定SRBM的參數，此處初始化SRBM網絡選擇以正態隨機分布，閾值初始化為0；最大迭代次數設定為100；sparsity Variance設定為0.1；稀疏度sparsity Target設定為0.02；稀疏代價sparsity Cost設定為3；參數表現模式選擇為“reconstruction”。最后，整套網絡通過將SRBM結構與反向傳播網絡BP相結合從而達成有監督降維，提高了網絡的全局性能。這是由于SRBM網絡學到的為一般化普適的概念化特征，僅能保障各層內特征映射局部最優卻不能整體最優，因此在頂層引入BP有監督訓練整個網絡，可將誤差信息反饋給SRBM層從而細調整個網絡的模型參數以達成不同類別天氣狀態的特征數據降維的差異化。使用BP網絡在matlab中只需要調用自帶的backpropagation函數即可。

考慮到輸入特征的維數，本文SRBM選擇3層較為適宜，即從72維先降維到30維，再降維到3維即可可視化通過SRBM降至3維的典型飛行參數特征集，如圖6所示。

由圖6可見，總體而言，SRBM降維得到的不同類別的典型飛參3維特征可較有效地達成一定程度的聚合，盡管仍有少量不同類別的特征點出現了重合，但相比線性PCA降維而言，降維效果獲得了較大的提升。下一節將進一步通過機器學習分類器的方法展示該降維提取特征對于飛行狀態識別的有效性。

5.3 基于DSRBM-GP的航空器飛行狀態識別

本研究的目標是利用機器學習的方式建立航空器的飛行狀況辨認識別模型，是一類典型的模式識別問題，涵蓋原始預處理的數據清洗、特征提取的特征工程、特征降維和建立分類器一系列流程。依據前述的高斯分類器原理，可以建立如下的基于高斯過程分類的飛行狀態識別模型。

第一步，分別從經過PCA和SRBM降維后的特征集中選擇適量的樣本(訓練集大小后文交叉驗證時說明)作為高斯分類器的訓練輸入。依據本文前述理論，將標記為正常天氣狀態(y=+1)的特征集作為一類，標記為異常天氣狀態(y=-1)的特征集作為另一類，初始化協方差矩陣，利用拉普拉斯近似法獲取協方差函數的最后超參數hyp1；

第二步，將待預測判定的樣本數據輸入對應于hyp1的高斯過程分類器，并依據式(29)獲取預測樣本數據劃分為+1類的預測概率。此時，若預測概率值大于0.5,則認定該樣本所屬的飛行天氣狀態為正常；否則，認定所處的天氣狀態為糟糕。

為了驗證所建立的飛行狀態識別模型，需要將上述預測判定的類別與實際標簽比對從而確定模型的識別準確率。本研究的問題是二分類問題，容易定義識別準確率公式如下：

為對比經PCA降維和SRBM降維后分類的效果，本文采用4折交叉驗證，即將經特征降維后的全體特征集樣本數據隨機等分成4組，其中3組作為模型的訓練集訓練基于高斯過程的狀態識別模型以確定高斯核參數，剩下1組作為測試集檢驗識別模型準確率；最后對4次交叉驗證的準確率取平均值，更能代表該模型的準確性。圖7展示了兩種降維算法在高斯過程分類下的四折交叉驗證結果，其中SRBM-GP分類準確率高達83.33%，而PCA-GP分類準確率僅為62.5%，容易得知經過SRBM降維提取的三維特征擁有較高的分類正確率。

進一步，為了更直觀展示經過兩種降維算法降維后在高斯過程分類器下的分類結果，借助兩種降維模型提取有效兩維特征輸入高斯過程分類器，可在二維等高斯概率線上展現各個測試點的分類結果。如圖8～9所示，容易更直觀地比對出：SRBM-GP算法的分類效果是遠高于PCA-GP算法的，與上面的交叉驗證結果相符，驗證了本文提出算法的有效性。

6 結論

本文圍繞航空器飛行狀態識別的目標建立了基于高斯過程分類器的識別算法。為驗證模型有效性，本文考慮到樣本數量，采用了四折交叉驗證取平均值作為模型分類正確性的標準，并將分類結果進一步作了二維可視化呈現，比對了經過主元分析和稀疏受限玻爾茲曼機降維后的特征，從而驗證了本文提出的基于深度稀疏玻爾茲曼機降維算法在高斯過程分類器下的分類正確性。

[1] 孫禾.航空器飛行狀態預測方法研究[D].天津：中國民航大學,2014.

[2] Inseok Hwang, Jesse Hwang, Claire Tomlin. Flight-Mode-Based Aircraft Conflict Detection using a Residual-Mean Interacting Multiple Model Algorithm[C]// AIAA Guidance, Navigation and Control Conference and Exhibit, August 11-14, 2003.

[3] Natasha A. Neogi, Asal Naseri. Using hidden markov models to detect mode changes in aircraft flight data for conflict resolution[C]// IEEE International Conference on Systems, Man, and Cybernetics, Taipei, Taiwan, October 8-11, 2006.

[4] Asal Naseri, Natasha A. Neogi. Stochastic hybrid models with applications to air traffic management[C]// AIAA Guidance, Navigation and Control Conference and Exhibit, August 20-23, 2007.

[5] E.Ronchieri,L.Pollini,M. Innocenti. Decentralized Control of a Swarm of Unmanned Aerial Vehicles[C]// AIAA Guidance, Navigation, and Control Conference and Exhibit, South Carolina, August 20-23, 2007.

[6] Erik de Vries, Kamesh Subbarao. Cooperative Control of Swarms of Unmanned Aerial Vehicles[C]// 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Florida, January 4-7, 2011.

[7] Qing WANG, Kaiyuan WU, Tianjiao ZHANG, Yi’nan KONG, Weiqi QIAN. Aerodynamic Modeling and Parameter Estimation from QAR Data of an Airplane Approaching a High-altitude Airport[J].Chinese Journal of Aeronautics. 2012, 25(3): 361-371.

[8] C. Edward LAN, Kaiyuan WU, Jiang YU. Flight Characteristics Analysis Based on QAR Data of a Jet Transport During Landing at a High-altitude Airport[J]. Chinese Journal of Aeronautics. 2012, 25(1): 13-24.

[9] B. Jia, C.F. Wei, J.F. Mao, R. Law, S. Fu, Q. Wu. Identification of flight state under different simulator modes using improved diffusion maps[J]. Optik—International Journal for Light and Electron Optics. 2016, 127(9): 3905-3911.

[10] 耿建中,姚海林.基于UKF的飛機飛行狀態估計[J]. 系統仿真技術及其應用, 2008, 10: 56-59.

[11] 張友民,張洪才,戴冠中等.非線性濾波方法及其在飛行狀態及參數估計中的應用[J]. 航空學報. 1994, 15(05): 620-626.

[12] 高原,倪世宏,王彥鴻等.一種基于改進量子遺傳算法的飛行狀態規則提取方法[J]. 電光與控制, 2011, 18(1): 28-31.

[13] 王潔寧,孫禾,趙元棣. 面向終端區航空器飛行狀態識別的HMM方法[J]. 航空計算技術,2013,02:1-5.

[14] 李軍亮,胡國才,韓維,柳文林.基于Elman網絡的某型直升機飛行狀態識別[J]. 火力與指揮控制,2015,12:57-60.

[15] 劉雨. 基于SVM的直升機飛行狀態識別方法及其應用研究[D].南昌：南昌航空大學,2016.

[16] 趙元棣,孫禾. 航空器飛行狀態預測的混合模型研究[J].飛行力學,2016,04:81-85+89.

[17] 谷潤平,黃磊,趙向領. QAR數據的數據融合算法[J]. 計算機系統應用,2016,01:136-140.

[18] H Bozdogan. Model selection and Akaike’s information criterion (AIC): The general theory and its analytical extensions[J]. Psychometrika.1987, 52(3), 345-370.

[19] Box,G.E., Jenkins,G.M., Reinsel,G.C. Time series analysis: forecasting and control[M]. John Wiley & Sons, 2011.

[20] Verwey W B, Veltman H A, Detecting short periods of elevated workload: A comparison of nine workload assessment techniques[J]. Journal of experiment psychology, 1996, 2(3), pp 270-285.

[21] B. Jia, C.F. Wei, J.F. Mao, R. Law, S. Fu, Q. Wu. Identification of flight state under different simulator modes using improved diffusion maps[J]. Optik—International Journal for Light and Electron Optics. 2016, 127(9): 3905-3911.

[22] Hawkins, F.H., Human Factors in Flight[M]. 2nd edn. Ashgate. Brookfield, VT ,1993.

[23] Globerson A, Chechik G, Pereira F, et al. Euclidean embedding of co-occurrence data[J]. Journal of Machine Learning Research, 2007, 8(10): 2265-2295.

[24] 吳春國,梁艷春,孫延鳳等.關于SVD與PCA等價性的研究[J].計算機學報，004,27(2):286-288.

[25] Salakhutdinov R, Murray I, On the Quantitative Analysis of Deep Belief Networks[C]// Proc of International Conference on Machine Learning, 2008, 872-879.

[26] Ackley D H, Hinton G E, Sejnowski T J. A Learning Algorithm for Boltzmann Machines[J]. Cognitive Science, 1985, 9(1): 147-169.

[27] ManceraL, Portilla J.L0-norm-based sparse representation through alternateprojection[C]// 2006: 2089-2092．

[28] Lee H, Ekanadham C, Ng A Y.Sparse deep belief net model for visual area V2[C]. 2007: 873-880．

Abnormal Flight States of Aircraft Identification Based on Deep Learning Method

WU Qi CHU Yinxue

(Shanghai JiaoTong University, Shanghai 200240, China)

The quick access recorder(QAR) retains the navigational information of all important flight parameters of the original flight, making it possible to analyze aircraft real-time conditions and ensure flight quality. According to the characteristics of high-dimensional large-scale QAR data, under the background of Big Data, different from the traditional mechanism modeling and analysis of aircraft flight state, the paper uses deep learning to establish a data-driven aircraft flight state recognition model. Based on the study of real QAR flight data, an abnormal flight state recognition program based on the Sparse Restricted Boltzmann Machine is developed. First of all, we use the wavelet de-noising translation method to pre-process the original flight data. And then, we select a series of typical flight parameters, extract the classical time-domain features of these parameters and the mixed entropy feature like Wavelet Singular Entropy to form the feature set. Then we use the Principal Component Analysis technique and the Sparse Restricted Boltzmann Machine to effectively reduce the feature set. Finally, we use four-fold cross validation method. We put the training set into the Gaussian process classifier as a last step. The experimental results show that the flight state recognition based on the Sparse Restricted Boltzmann Machine-Gaussian process classification has high classification accuracy.

flight state recognition; deeping learning; gaussian process

10.19416/j.cnki.1674-9804.2017.03.013

吳奇男，博士，副教授。主要研究方向：人機交互，深度學習，大數據分析。Tel: 021-34204492,E-mail: wuqi7812@sjtu.edu.cn

V226

：A

儲銀雪男，碩士。主要研究方向：深度學習。Tel: 021-34204492,E-mail: chuyinxue@sjtu.edu.cn