礦山生產能力可信度的MonteCarlo模擬與應用研究

楊蕾綺，劉文君，文 磊，李 兵

(1.南華大學經濟管理學院，湖南 衡陽 421001；2.南華大學核能經濟與管理研究中心，湖南 衡陽 421001；3.南華大學核資源工程學院，湖南 衡陽 421001)

礦山生產能力可信度的MonteCarlo模擬與應用研究

楊蕾綺1，2，劉文君1，2，文 磊3，李 兵3

(1.南華大學經濟管理學院，湖南 衡陽 421001；2.南華大學核能經濟與管理研究中心，湖南 衡陽 421001；3.南華大學核資源工程學院，湖南 衡陽 421001)

地下礦山生產能力的設計具有廣泛的不確定性，為減少生產能力決策風險，建立了礦山生產能力可信度的Monte Carlo模擬方法。以黑龍江某鉬礦首采中段的生產能力方案模擬為例，分別進行了按同時回采礦塊數、礦山開采年下降速度和新水平準備時間的生產能力可信度的Monte Carlo方法模擬，綜合分析表明，300×104t/a、500×104t/a、750×104t/a的礦山生產能力方案的可信度分別為100%、99.1%～88.4%、84.0%～9.85%，模擬結果可為生產能力設計提供參考。

礦山生產能力可信度；Monte Carlo法；同時回采礦塊數；年下降速度

0 引 言

礦山生產能力是礦山企業建設與生產的關鍵指標，直接影響礦山投資規模、基建工程量大小、投產和投產時間及礦山企業的運營效益等。礦山生產能力的確定主要考慮以下因素[1-4]：①礦床開采自然條件，如儲量、品位、礦床產狀及分布等；②礦床開采技術經濟條件，如投資，水、電、設備供應，外部運輸等；③市場需求，如資源區域分布、產品需求分布、產品價格走勢等。其中，礦床開采自然條件和技術經濟條件主要是從技術上分析可能達到的生產生能力，而市場需求主要從經濟上優化生產能力。目前，金屬礦山按技術可能性確定生產能力的方法主要有三種：按可布礦塊數、按礦山開采年下降速度和按新水平準備，最終設計的礦山企業的生產能力應同時滿足以上三個條件，本文僅從技術方面考慮礦山實現生產能力的可能性，以供礦山生產能力決策提供參考。

由于影響礦山生產能力的因素(如年下降速度、地質儲量、礦床產狀等)具有不確定性，學者們用BP神經網絡、模糊綜合評價法、灰色理論、遺傳算法等方法優化和確定礦山生產能力[5-7]。同時，Monte Carlo方法被廣泛用來進行隨機事件的模擬、分析和評價[8-11]。與BP神經網絡、遺傳算法等方法相比，Monte Carlo模擬方法的優點是模擬的精度高，方法簡單，缺點是模擬次數多，一般當模型不復雜時，可選用Monte Carlo模擬方法。為此，本文采用Monte Carlo方法模擬礦山生產能力，并開展應用研究。

1 基于Monte Carlo方法的礦山生產能力可信度數值模擬

Monte Carlo方法的實質是通過大量隨機試驗，利用概率論解決問題的一種數值方法。基本思想是當所求解問題是某種隨機事件出現的概率，或者是某個隨機變量的期望值時，通過某種“實驗”的方法，以這種事件出現的頻率估計這一隨機事件的概率，或者得到這個隨機變量的某些數字特征，并將其作為問題的解。

礦山生產能力可信度Monte Carlo數值模擬計算步驟如下。

1)確定礦山生產能力的計算模型，見式(1)。

A=f(X1，X2，…，Xn)

(1)

式中：A為礦山生產能力，104t/a；f為礦山生產能力的計算模型，X1，X2，…，Xn分別為影響生產能力的因素。常用的技術可能性確定生產能力的模型有可布礦塊數模型、開采年下降速度模型和新水平準備模型，分別見式(3)、式(4)和式(5)。

2)擬訂目標中段生產能力，根據礦山綜合技術開采條件和市場經濟分析，初步擬訂目標中段生產能力的幾種方案，以Yj表示第j種方案，生產能力為Y。

3)分析確定影響生產能力因素的概率分布Ψ(Xi)。

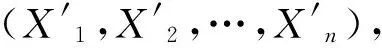
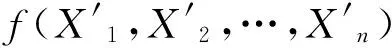
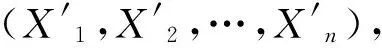
7)礦山中段生產能力可信度按式(2)計算。

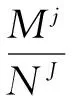
(2)

式中，pj為第j種目標生產能力方案的實現概率。

2 應用研究

2.1工程概況

黑龍江某鉬礦山為新建礦山，選擇380～80 m作為首采區，階段高度為60 m，320 m中段為首采中段，320 m中段礦體資源儲量(Mo≥0.1%)為1 435.91×104t，平均品位為0.145 4%，鉬金屬量20 871.67 t。采用大直徑深孔階段空場嗣后充填采礦，采場鏟運機出礦、中段汽車運輸、斜井膠帶連續提升至選礦廠。

根據礦山企業發展需求，提出了300×104t/a、500×104t/a和750×104t/a三種生產能力方案，通過生產能力方案可信度的Monte Carlo數值模擬，確定礦山生產能力方案。

2.2基本假設

1)礦山主要生產機械設備生產能力滿足設計要求，不考慮充填系統與選礦系統對生產能力的制約。

2)考慮基建工程推進速度，首采中段采用單中段生產，待礦山達產后，可考慮2個中段同時生產。

3)生產能力模型中所有不確定性參數假設服從標準正態分布。

2.3按可布礦塊數的生產能力的模型與參數

2.3.1 可布礦塊數的生產能力模型

首采中段選在320 m，各主要回采工藝不同時進行，同時回采礦塊數確定生產能力按式(3)計算。

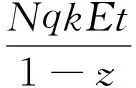
(3)

式中：A為礦山年生產能力，t/a；N為生產中段可布的礦塊總數，個；k為礦塊利用系數；q為礦塊生產能力，t/d；z為副產礦石率，%；E為地質影響系數；t為年工作日，d，t=330 d。

2.3.2 模型參數取值

N：首采中段礦塊布置如圖1所示，可布置的塊礦數經計算大致范圍為25～45塊。

圖1 礦塊布置圖

q：根據采礦方法和設備等條件，設定礦塊的生產能力為3 600 t/a，由于受到開采條件和工程設備的影響，礦塊生產能力有一定的波動性，本設計礦塊生產能力取值在2 000～4 000 t/a。

k：采用大直徑深孔嗣后充填采礦法，礦山礦塊布置的比較疏松，礦塊的利用系數比較高，參考相似大型金屬礦山資料選擇礦塊利用系數取0.25～0.35。

z：該礦山是鉬鉛鋅多金屬大型礦山，在300 m標高以上礦體夾石含量比較高，副產礦石率波動比較大，取5%～20%。

E：該礦山處在東北地區，由于地質構造和溫度等原因對礦山開采有一定的影響，取地質影響系數0.8～1.0。

2.4按年下降速度的生產能力的模型與參數

2.4.1 年下降速度的生產能力模型

按開采年下降速度確定中段生產能力按式(4)計算。

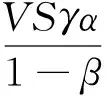
(4)

式中：A和E同式(3)；V為開采可行的年下降速度，m/a；S為中段可利用礦體水平面積，m2；γ為礦石容重，2.72 t/m3；α為綜合回收率，%；β為礦石貧化率，%；Z為礦體傾角修正系數。

2.4.2 模型參數取值

V：該礦山是鉬鉛鋅多金屬大型礦山，礦體水平面積比較大使開采年下降速度不大，但由于采用了大型的采掘設備使年下降速度有所增快，所以取開采可行的年下降速度在12～20 m。

S：首采中段的可利用礦塊不是連續的，這就給連續開采帶來了一定的困難，在開采礦塊選擇上要考慮礦石含量、開采成本等問題，就需要對分散的不能構成規模生產的礦塊先不予開采，使中段可利用礦體水平面積難以精確計算，取16×104～22×104m2。

α：采用的是大直徑深孔嗣后充填采礦法，該方法使礦石的綜合回收率很高，可以達到85%～95%。

β：礦房回采后采用采用膠結充填體，礦房的貧化率在5%～10%，礦柱回采后采用非膠結充填，礦柱貧化率在5%～15%，綜合考慮礦石貧化率取5%～15%。

Z：該礦山礦體隨著開采深度加大傾角也越來越大深部礦體傾角幾乎達到了90°，該礦體修正系數取在0.85～0.95較合理。

2.5按新中段準備時間的生產能力的模型與參數

2.5.1 新中段準備時間的生產能力模型

為保證礦山能持續生產，必須使新階段開拓、采準等準備時間小于開采一個階段所需的時間，因此，礦山生產能力受到新階段準備時間的限制。

新階段開拓、采準等準備時間，根據設計礦山實際采用的機械水平和掘進工作條件及技術管理水平等情況，通過排采掘進度計劃得出。

新中段巷道布置如圖2。輔助斜坡道長502 m，兩條穿脈巷道長973 m，回風石門長22.5 m，運輸大巷長513 m，回風大巷長505 m。新中段采掘總長度S為2 515.5 m。

圖2 開拓巷道布置圖

新中段巷道掘進不能平行進行，一年工作11個月，新階段準備時間T按式(5)計算，中段生產能力A按式(6)計算。

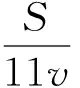
(5)

式中：T為新階段準備時間，a；v為井巷掘進速度，m/月。

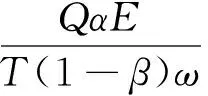
(6)

式中：A、α、β和E同式(3)、式(4)和式(5)；Q為生產中段可利用礦量，1 435.9萬t。

2.5.2 模型參數取值

V-根據設計單位提供的井巷掘進進度和實際井巷掘進進度綜合確定，取120～180 m/月；α、β、E取值同式(4)；ω-超前系數值視礦床埋藏要素穩定情況而定，礦床埋藏要素穩定，有用礦物分布均勻，ω=1.2～1.5。

2.6首采中段生產能力Monte Carlo模擬與分析

按照上面介紹的礦山生產能力可信度Monte Carlo數值模擬計算程序和步驟，模擬生產能力見表1。

從表1中可看出：①首采區設在320 m，達到300×104t/a生產規模設計要求的可信度均為100%；②達到500×104t/a生產規模設計要求的可信度均達到88.4%以上；③按年下降速度和新中段準備時間模擬的年生產能力達到750×104t/a的生產規模設計要求的可信度很小，需多中段作業。

綜合礦山的采礦工藝、設備條件、礦體賦存條件，建議首采區采用300×104～500×104t/a生產規模，待具備多中段生產條件時，將礦山生產能力提高到750×104t/a。

3 結 論

1)用Monte Carlo模擬礦山生產能力可信度，綜合考慮了各種不確定性因素，對礦山生產能力設計更為科學合理。

2)用Monte Carlo模擬了黑龍江某鉬礦首采中段生產能力的可信度，首采區采用300×104t/a、500×104t/a、750×104t/a的礦山生產能力方案的可信度分別為100%、99.1%～88.4%、84.0%～9.85%，模擬結果可為生產能力設計提供參考。

[1] 羅周全，管佳林，王益偉，等.地下金屬礦山生產規模優化確定方法[J].中南大學學報：自然科學版，2013，44(7)：2875-2880.

[2] 張幼蒂，姬長生.大型礦山生產規模及其相關決策要素綜合優化[J].中國礦業大學學報，2000，29(1)：15-19.

[3] 鄭明貴，蔡嗣經.地采金屬礦山生產規模確定的泰勒公式研究[J].江西理工大學學報，2007，28(3)：21-25.

[4] 王革民，陳建宏，劉浪.現代礦山開采生產規模優化準則綜述[J].礦業研究與開發，2012，32(5)：1-5，19.

[5] 張誠，黃彬.基于BP神經網絡的金屬礦山生產規模優化研究[J].采礦技術，2016，16(1)：73-74.

[6] Gligoric Z，Beljic C Gluscevic，et al.Hybrid model of evaluation of underground lead-zinc mine capacity expansion project using Monte Carlo simulation and fuzzy numbers[J].Simulation-Transactions of the Society for Modeling and Simulation International，2011，87(8)：726-742.

[7] 饒運章，黃凱龍，李闖，等.露天礦山轉地下開采過渡時期生產規模的模糊綜合優化[J].有色金屬科學與工程，2011，2(5)：61-64.

[8] 關維娟，陳明強，何剛，等.基于MonteCarlo隨機模擬的煤礦工作面環境評價模式研究[J].安全與環境學報，2016，16(3)：326-330.

[9] 周雨凡，胡明華，張穎，等.基于Monte-Carlo模擬的進場排序不確定性研究[J].交通信息與安全，2016，34(4)：22-28.

[10] Booth AJ，Marshall AM，Stace R.Probabilistic analysis of a coal mine roadway including correlation control between model input parameters[J].Computers and Geotechnics，2016，74：151-162.

[11] Viveros P，Zio，E，F Kristjanpoller，et al.Integrated system reliability and productive capacity analysis of a production line.A case study for a Chilean mining process[J].Journal of Risk and Reliability，2012，226(3)：305-317.

MonteCarlosimulationsofthereliabilityofminecapacityanditsapplication

YANG Leiqi1，2，LIU Wenjun1，2，WEN Lei3，LI Bing3

(1.School of Economics and Management，University of South China，Hengyang421001，China；2.Research Center of Nuclear Energy Economics and Management，University of South China，Hengyang421001，China；3.School of Nuclear Resources Engineering，University of South China，Hengyang421001，China)

There is great uncertainty in the process of design underground mine’s capacity.In order to reduce its decision risk，the Monte Carlo simulations of the reliability of mine capacity is established.Taking the capacity simulations of initial mining level of a molybdenum mine in Heilongjiang as an example，the Monte Carlo simulations of the reliability of mine capacity is separately carried out with the design method of the numbers of simultaneously mining block，and the design method of mining decreasing speed per year and the design method of new level preparation time.Comprehensive analysis shows that the reliability of mine capacity of300×104t/a，500×104t/a and750×104t/a are respectively100%，99.1%～88.4% and84.0%～9.85%，and the simulation results can provide a reference for mine capacity design.

reliability of mine capacity；Monte Carlo simulation；numbers of simultaneously mining block；mining decreasing speed per year

2017-01-02責任編輯：趙奎濤

國家自然科學基金項目資助(編號：71540011，50974076)

楊蕾綺(1993-)，女，湖南衡陽人，碩士研究生，攻讀南華大學應用經濟學專業，主要從事礦業經濟與核能經濟與系統工程方面的研究工作，E-mail：544528641 @qq.com。

劉文君(1978-)，男，博士，陜西山陽人，2011年畢業于日本神戶大學經濟學專業，副教授，碩士生導師，主要從事核能經濟與系統工程方面的研究工作，E-mail：liuwenjun@usc.edu.cn。

TD214

：A

：1004-4051(2017)09-0038-04