AN EXPLICIT FORMULA FOR THE FOURTH MOMENT OF TWO-TERM EXPONENTIAL SUMS

AI Xiao-chuan,CHEN Hua,ZHANG Si-lan

(1.Department of Applied Mathematics,School of Science,Naval University of Engineering, Wuhan 430033,China)

(2.School of Science,Hubei University of Technology,Wuhan 430068,China)

(3.College of Science,Huazhong Agricultural University,Wuhan 430070,China)

AN EXPLICIT FORMULA FOR THE FOURTH MOMENT OF TWO-TERM EXPONENTIAL SUMS

AI Xiao-chuan1,CHEN Hua2,ZHANG Si-lan3

(1.Department of Applied Mathematics,School of Science,Naval University of Engineering, Wuhan 430033,China)

(2.School of Science,Hubei University of Technology,Wuhan 430068,China)

(3.College of Science,Huazhong Agricultural University,Wuhan 430070,China)

The fourth power mean of two-term exponential sums is studied in this paper. By elementary and algebraic methods,an explicit computation formula and a transform formula are proposed,which extend the original research results and discover the essential relation between fourth moment and congruence equations.

two-term exponential sums;mixed exponential mean;fourth power mean;transform formula

1 Introduction

For integers m,n,q,k with q≥3,k≥2,we def i ne a two-term exponential sums

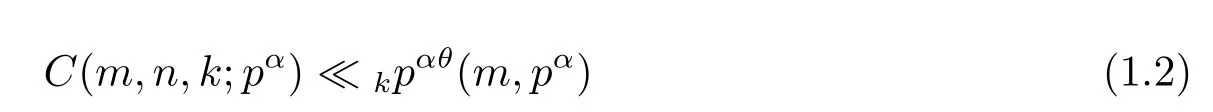
or(p,m)=1,where θ=2/3 for k=3 and θ=3/4 for k＞3.Afterwards,Hua[9]showed that θ=1/2 for all k≥2 by using Weil’s estimate for exponential sums over f i nite f i elds.Till now,many improvements for(1.2)were made by Loxton,Vaughan and Smith[5,6,11]. Carlitz[7,8]studied the computation problem of the two-term exponential C(m,n,k;p) over fi nite fi elds and obtained the computational formulas for k=3 and k=p+1.As to the two-term exponential sums with Dirichlet character C(m,n,k,χ,q)= Xu[13],Liu[3],Chen[14,15],Ai[16]and Calderon[1]also acquired a lot of research results.More,about the three-term exponential sums,there were also some interesting results[17-19].

Though the single value of C(m,n,k;q)is irregular,the high power means that value of C(m,n,k;q)owns graceful arithmetical properties and it in turn becomes an interesting focus for many attentions.In 2010,Liu[4]acquired the computational formula of the fourth mean value,i.e.,when p is an odd prime with(n,p)=1,then

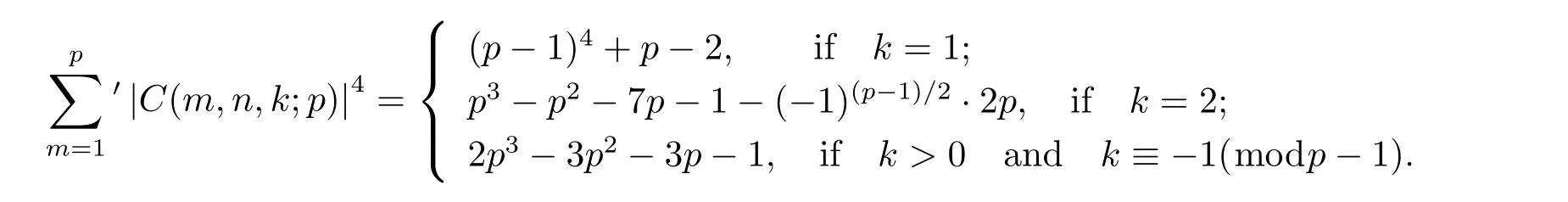
In 2011,Wang,Zhang[12]studied the computation problem of the fourth moment of two-term mixed exponential sums with elementary algebraic method.They proved that when p is a prime and(n,p)=1,then

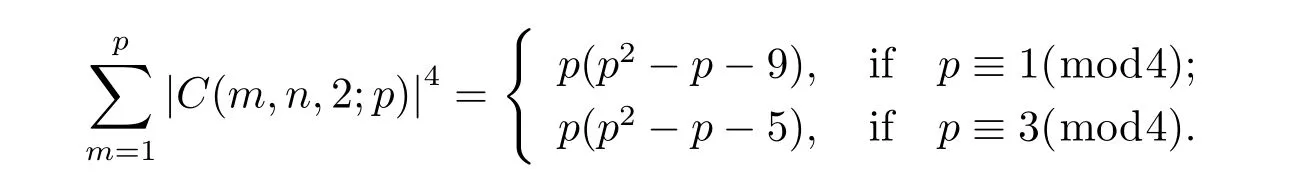
When p is a prime,(n,p)=1 and(3,p-1)=1,then p

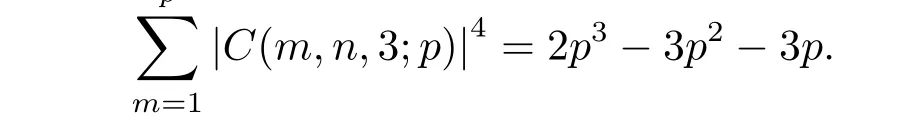
Unfortunately,though Liu,Wang got the explicit formulas ofwith k≥1,k=-1,1,2,3(mod(p-1)),the result under the condition k≥1,k≡5(mod(p-1)) was not solved.In this paper,this computation problem will be solved and the explicit formulas will be given.Moreover we shall give a transform formula and a lower bound formula for the fourth moment of two-term exponential sums.The main results are the following two theorems.

Theorem 1.1 Let p be a prime with p≥5,(5,p-1)=1,n be an integer with (n,p)=1,then for k≥1,k≡5(mod(p-1)),we have

Theorem 1.2 Let p be a prime with p≥3,(k,p-1)=1,n be an integer with (n,p)=1,then we have

2 Preliminaries

To prove the main results,necessary lemmas are listed and proved as below.

Lemma 2.1 For arbitrary integers a,b,c,let p be an odd prime with(a,p)=1 and denote N1as the number of the solutions of the congruence equation ax2+bx+c≡0(mod p), then

Proof From Theorem 3.5.1 in ref.[10],we immediately get the result.

Lemma 2.2 Let p be an odd prime,N2denote the number of the solutions of the congruence equation c2-c+1≡0(modp),then

And if p≡1,-5(mod12),1,p are not solutions.

Proof Since(1,p)=1,by Lemma 2.1,we have

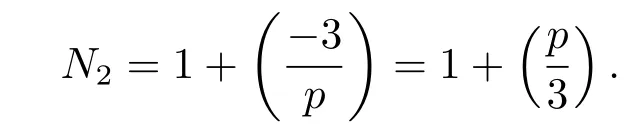
In conclusion,we have

And straight forward calculation shows that 1,p are not solutions.

Proof See Theorem 7.8.2 in ref.[10].

Lemma 2.4Let p be an odd prime,k be an odd positive integer anddenote the number of the solutions of the congruence equation

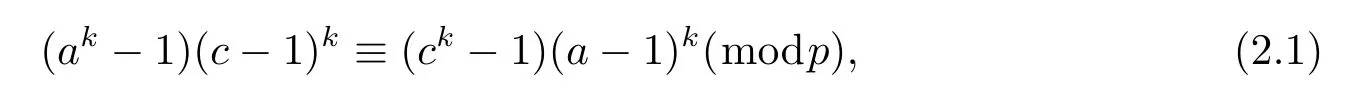
where a,c are integers with 2≤a,c≤p-1,then we have Nk,p≥2p-5.

Proof It is obviously to show that a≡c(mod p)is fi t for equation(2.1),now we consider the case c≡a(mod p).

After substituting c≡a(mod p)into the left part of formula(2.1),we have

Again,c≡a(mod p)is substituted into the right part of(2.1).Since k is an odd integer,then

Therefore

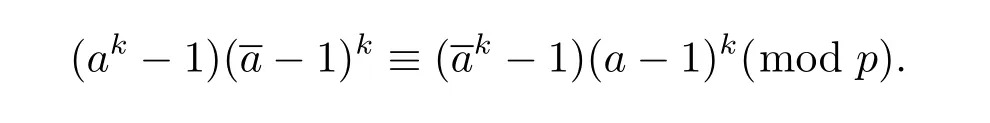
So c≡a(mod p)is also fi t for equation(2.1).

Moreover a≡c(mod p)and a≡c(mod p)have the same solution(a,c)=(p-1,p-1). Hence Nk,p≥2p-5.

Lemma 2.5Let p be a prime with p＞3 and N3denote the number of the solutions of the congruence equation

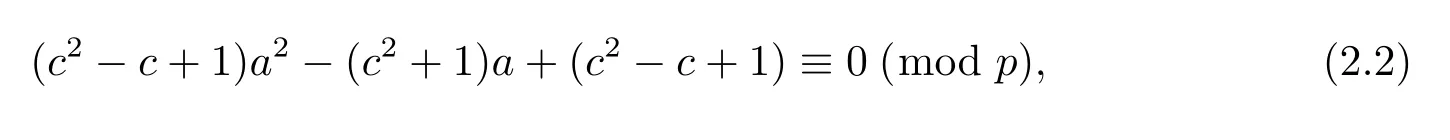
where a,c are integers with 2≤a,c≤p-1,then we have

Proof Case 1For a fi xed c,2≤c≤p-1,if c2-c+1 6≡0(mod p),from Lemma 2.1, the number of the solutions of equation(2.2)is

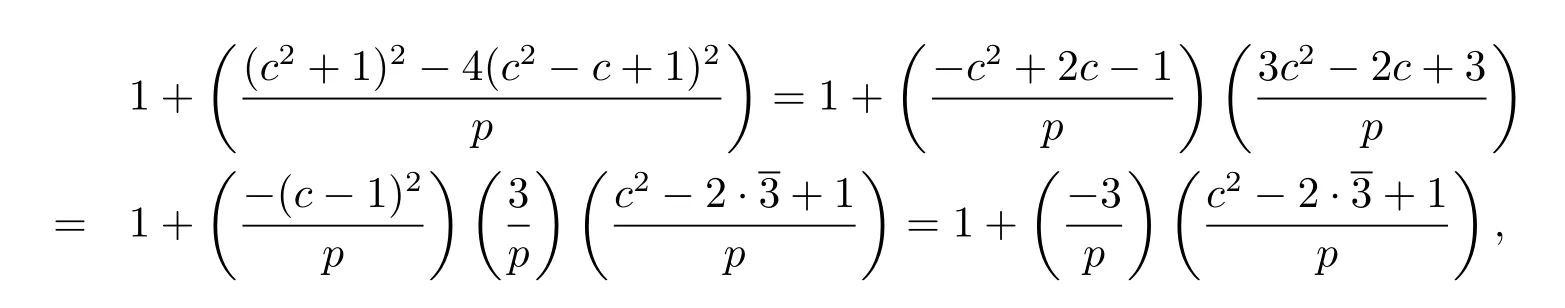
where 3 satis fi es 3·3≡1(mod p).If a≡1(mod p)satis fi es equation(2.2),then c≡1(mod p);If a≡0(mod p)satis fi es equation(2.2),then c2-c+1≡0(mod p),that contradicts.

Case 2 For a fi xed c,2≤c≤p-1,if c2-c+1≡0(mod p),then equation(2.2)is (c2+1)a≡0(mod p),namely ca≡0(mod p),therefore congruence equation(2.2)has nosolution.So we have

By using Lemma 2.3,we have

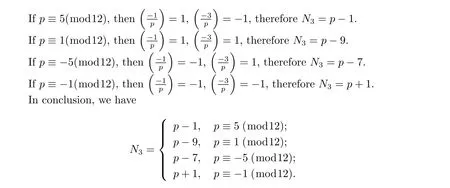
Lemma 2.6 Let p be a prime,p＞5 and N5,pdenote the number of the solutions of the congruence equation

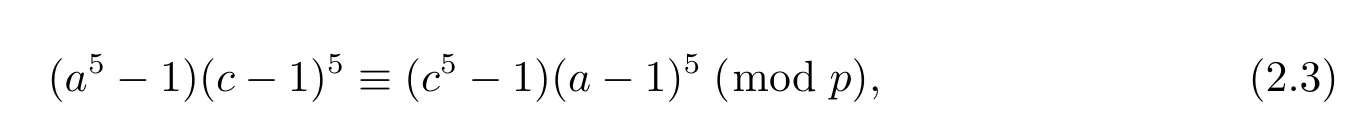
where a,c are integers with 2≤a,c≤p-1,then we have

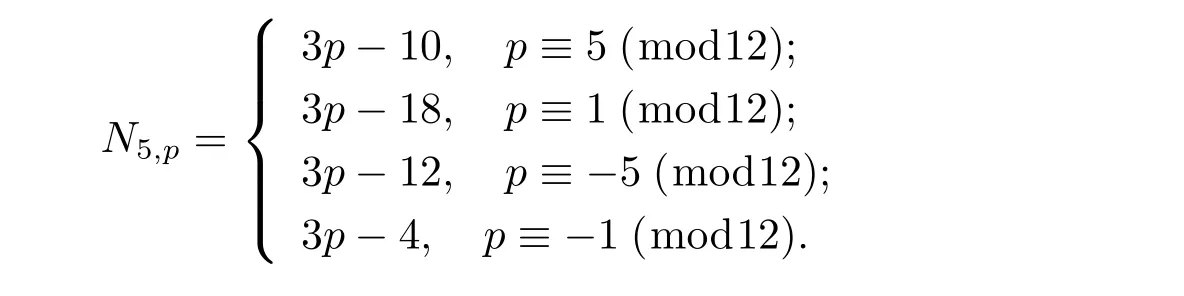
Proof By using factorization method,we know that equation(2.3)equivalents to

Noting that p is a prime with p＞5 and 2≤a,c≤p-1,we have

where||denotes the number of the elements of the set.

(a)It is obviously that S1∩S2={(p-1,p-1)}and thus|S1∩S2|=1.

Now we can see that the case is similar to case(b).Therefore we have if p≡1(mod4),then |S2∩S3|=2;if p≡-1(mod4),then|S2∩S3|=0.So

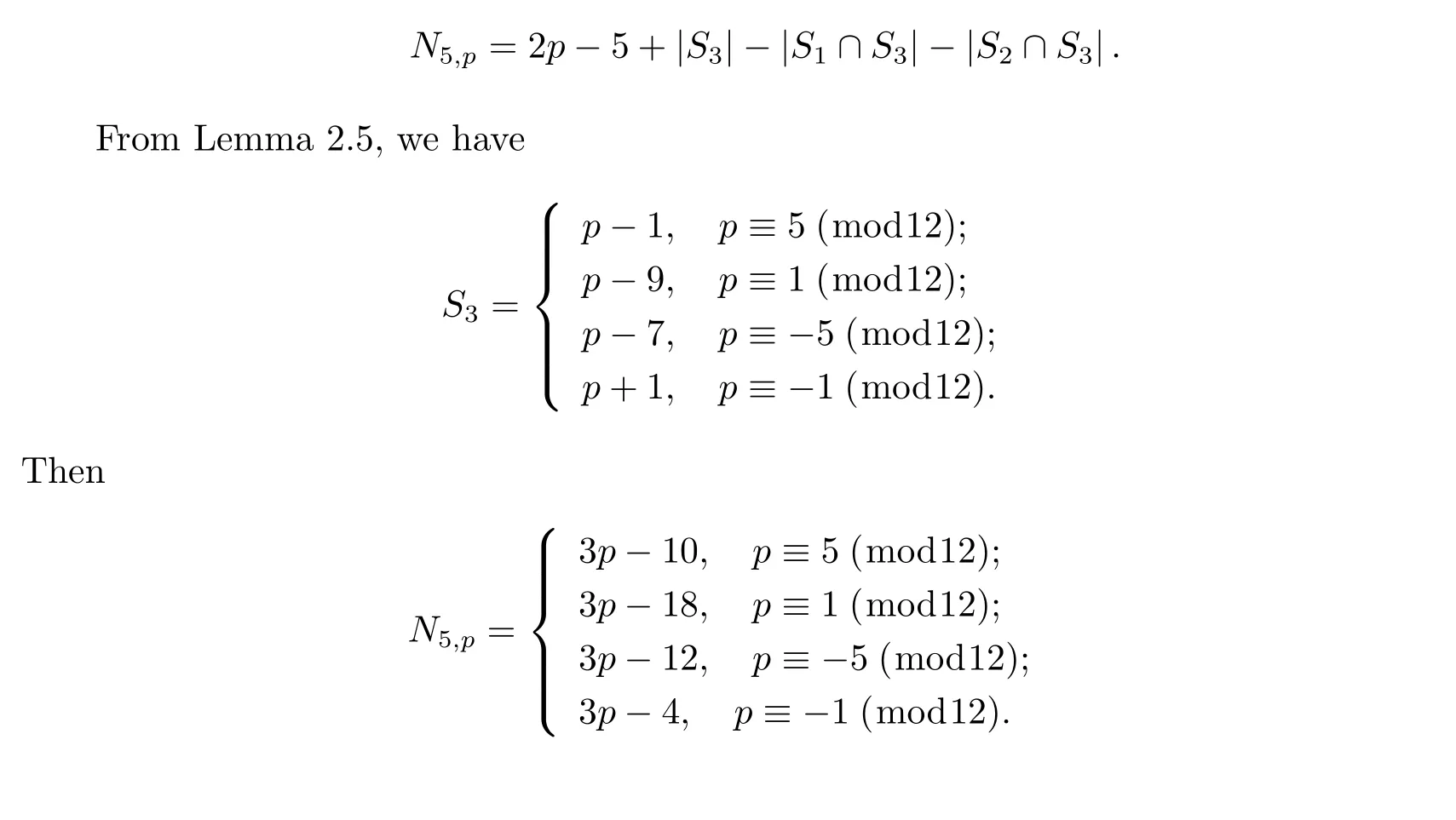
Lemma 2.7Let p be an odd prime with(n,p)=1 and(k,p-1)=1,then we have

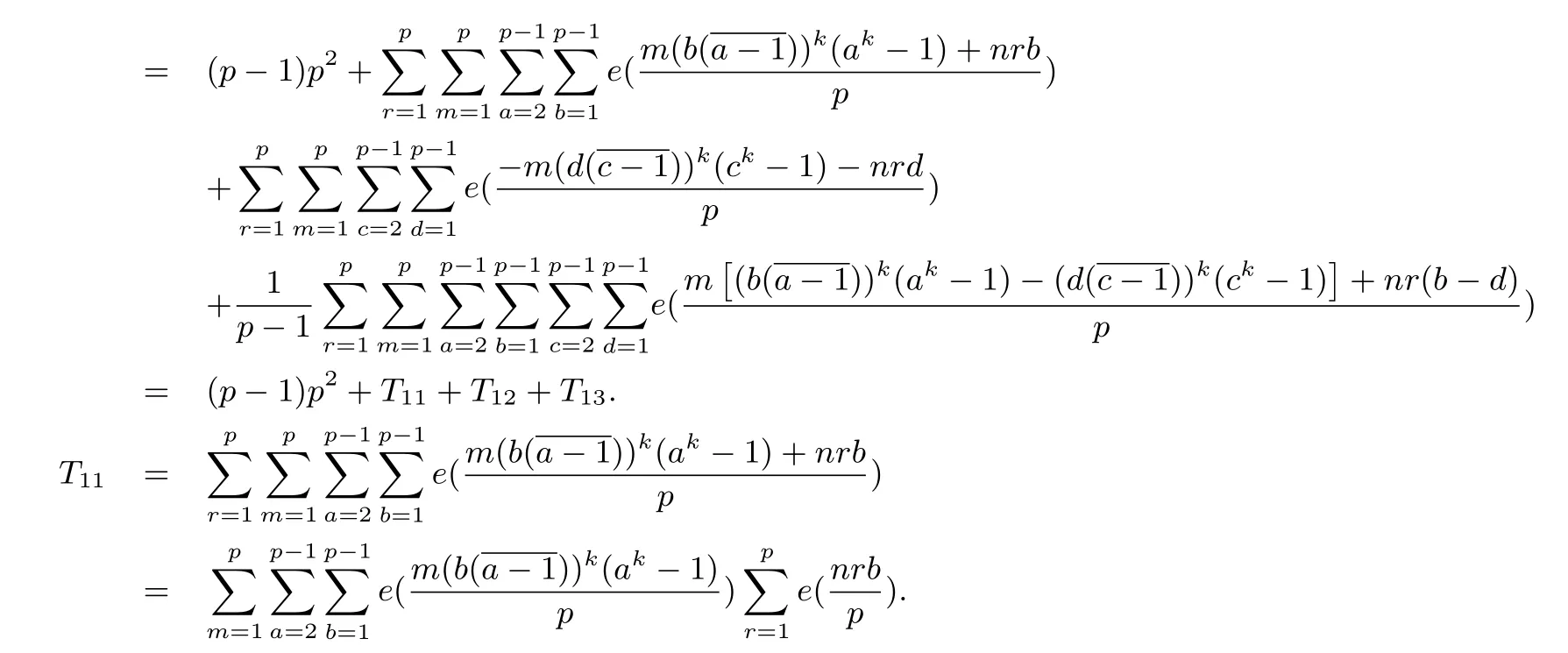
With the condition(n,p)=1 and from the trigonometric identity,

3 Proof of the Theorems

First we prove Theorem 1.1.

Proof By Lemma 2.7,we have

From Lemma 2.6,we have

This proves Theorem 1.1.

Finally we complete the proof of Theorem 1.2.

Proof By Lemma 2.7 and Lemma 2.4,we have

[1]Calderon C,Develasco M J,Zarate M J.An explicit formula for the fourth moment of certain exponential sums[J].Acta Math.Hungar,2011,130(3)：203-222.

[2]Darvenport H,Heibronn H.On an exponential sum[J].Proc.London Math.Soc.,1936,41：49-53.

[3]Liu H N.Mean value of mixed exponential sums[J].Proc.Amer.Math.Soc.,2008,136(4)：1193-1203.

[4]Liu H N.Mean value of some exponential sums and applications to Kloosterman sums[J].J.Math. Anal.Appl.,2010,361(4)：205-223.

[5]Loxton J H,Smith R A.On Hua’s estimate for exponential sums[J].J.London Math.Soc.,1982, 26(2)：15-20.

[6]Loxton J H,Vaughan R C.The estimate for complete exponential sums[J].Canada Math.Bull., 1995,26(4)：442-454.

[7]Carlitz L.Explicit evaluation of certain exponential sums[J].Math.Scand.,1979,44：5-16.

[8]Carlitz L.Evaluation of some exponential sums over a f i nite f i eld[J].Math.Nachr.,1980,96：319-339.

[9]Hua L K.On exponential sums[M].Peking,N.S.：Sci.Record,1957.

[10]Hua L K.Introduction to number theory[M].Beijing：Sci.Press,1979.

[11]Smith R A.On n-dimensional Kloosterman sums[J].J.Number Theory,1979,11：324-343.

[12]Wang T T,Zhang W P.Mean value of the mixed fourth and sixth exponential sums[J].China Sci., 2011,41(3)：265-270.

[13]Xu Z F,Zhang T P,Zhang W P.On the mean value of the two-term exponential sums with Dirichlet characters[J].J.Number Theory,2007,123(2)：352-362.

[14]Chen H,Chen J H,Cai G X,Ai X C,Zhang S L.Explicit formulas for the fourth moment of mixed exponential sums[J].J.Number Theory,2013,133(5)：1484-1491.

[15]Chen H,Ai X C,Cai G X.A note on mean value of mixed exponential sums[J].J.Number Theory, 2014,144(11)：234-243.

[16]Ai X C,Chen J H,Chen H,Zhang S L.Explicit formulas for the fourth moment of certain two-term exponential sums[J].J.Comp.Model.New Tech.,2014,18(12A)：232-239.

[17]Ai X C,Chen J H,Chen H,Zhang S L.Explicit formulas for the fourth moment of three-term exponential sums[A].2014 International Joint Conference on Applied Mathematics,Statistics and Public Administration(IJAMSPA 2014)[C].Changsha：ISBN：978-1-60595-187-4.

[18]Ai X C,Chen J H,Zhang S L,Chen H.Researching the relation between the three-term exponential sums and the system of the congruence equations[J].J.Math.,2013,33(3)：535-540.

[19]Ai X C,Chen J H,Chen H,Zhang S L.Explicit formulas for the mean value of high gauss sums.J. Math.,2015,35(4)：941-944.

二項(xiàng)指數(shù)和四次混合均值的計(jì)算

艾小川1,陳華2,張四蘭3

(1.海軍工程大學(xué)理學(xué)院應(yīng)用數(shù)學(xué)系,湖北武漢430033)
(2.湖北工業(yè)大學(xué)理學(xué)院,湖北武漢430068)
(3.華中農(nóng)業(yè)大學(xué)理學(xué)院,湖北武漢430070)

本文研究了二項(xiàng)指數(shù)和四次均值的計(jì)算問(wèn)題.利用初等數(shù)論及代數(shù)數(shù)論的方法獲得了一個(gè)精確的計(jì)算公式以及一個(gè)轉(zhuǎn)換公式,推廣了已有的結(jié)果,揭示了均值計(jì)算與同余方程組的本質(zhì)聯(lián)系.

二項(xiàng)指數(shù)和;混合均值;四次均值;轉(zhuǎn)換公式

O156.2

A

0255-7797(2017)05-0945-11

?Received date：2015-09-06Accepted date：2015-11-25

Supported by National Natural Science Foundation of China(61502156); NSF Grants of Naval University of Engineering(HGDQNSQJJ15001);NSF Grants of Hubei Province (2014CFB189).

Biography：Ai Xiaochuan(1978-),female,born at Nanjing,Jiangsu,lector,major in number theory and cryptography.

Chen Hua.

2010 MR Subject Classif i cation：11T23;11T24