噴灌機全噴灑域與疊加域水量分布特性的靜態模擬

陳 震，段福義，范永申，賈艷輝，黃修橋（中國農業科學院農田灌溉研究所/河南省節水農業重點實驗室，新鄉 453002）

噴灌機全噴灑域與疊加域水量分布特性的靜態模擬

陳 震，段福義，范永申，賈艷輝，黃修橋※
（中國農業科學院農田灌溉研究所/河南省節水農業重點實驗室，新鄉 453002）

該文研究噴灌機噴頭組合噴灑特性，針對大型平移式噴灌機NelsonR3000、O3000旋轉折射式噴頭，開展試驗測量其單噴頭水量分布并計算其噴灑均勻系數（Christiansen uniformity， CU）、分布均勻系數（distribution uniformity，DU）。用MATLAB編程模擬了2噴頭和多噴頭組合，針對多噴頭組合，分析和區分全噴灑域和疊加域，計算2種噴頭全噴灑域與疊加域的CU、DU和平均噴灑強度（mean spraying intensity，MSI），全面掌握并評價噴頭水力性能。結果顯示：在安裝壓力調節器情境下，R3000單噴頭在壓力150 kPa、O3000單噴頭在壓力200 kPa時，CU、DU值最大。2個噴頭組合無法展現噴灌機噴頭組合效果。R3000多噴頭組合全噴灑域內，CU最大值68%，DU隨噴頭間距的增大逐漸上升；O3000多噴頭組合CU、DU最大值分別為72%、57%。疊加域內R3000、O3000噴頭CU、DU、MSI值高于全噴灑域，但達不到行噴CU≥85%的要求，可能由于計算CU、DU等的數據點多、單噴頭數據不理想、常規測量方法測量點少且在疊加域內等原因。該文發現當前大型噴灌機的噴頭間距組合不是CU、DU最優組合，區分了噴頭噴灑組合后疊加域和全噴灑域，并分別計算疊加域和全噴灑域CU、DU和MSI，為噴灌機系統的安裝設計提供了一種參考。

噴頭；均勻度；壓力; Nelson R3000；O3000；疊加法；噴灑組合

0 引 言

噴灌是當前主要的灌水方式之一，截止2015年中國噴灌面積達到了3 204.68×103hm2[1]。隨著土地的流轉，在大田尺度上大型噴灌機灌溉具有很大的優勢。當前國內外關于大型噴灌機的變量灌溉、分區控制等研究逐步深入[2-4]。其中，控制改變噴灌機的噴頭噴灑范圍、噴灑強度是實現變量、變域灌溉的一種主要方式[5-8]。目前噴灌機上常用Nelson R3000和O3000折射式噴頭，低壓、具有很好的抗風性能，在現在大型噴灌機上受到廣泛的應用[9-11]。

噴頭的性能是決定噴灌效果的基礎和前提，而噴頭性能通常通過工作壓力、流量、噴頭均勻性、噴灑強度、噴灑半徑以及多噴頭組合效果來衡量。噴頭的均勻性常用的評價指標有噴灌均勻系數（Christiansen uniformity，CU）和分布均勻系數（distribution uniformity，DU)[12-17]，其中根據噴灌均勻系數定義和計算方式的不同，可分為基于平均偏差的均勻系數、基于標準偏差的均勻系數、強調部分水量特征的分布均勻系數、基于概率分布函數的均勻系數和基于空間分布函數的均勻系數5大類，不同的評價指標針對性不同[13]。噴頭的均勻性受組合間距、冠層等影響，噴灌水量噴灑到土壤，存在土壤再分配的過程[18]。關于噴頭的組合問題，韓文霆等[15]試驗研究了基于扇形通孔動靜片調節器的變量噴頭在系統不同壓力工況下組合噴灌時的水量分布及噴灌均勻度等水力性能，并與傳統圓形噴灑域噴頭進行了對比；此外針對Nelson R33噴頭三角形組合方式采用線性插值、立方插值、三次樣條插值的兩次插值法、距離插值法和平面插值法計算了克里斯琴森均勻度并使用Sprinkler3D和SIUEW1.0 2個軟件計算組合均勻度[17]。江蘇大學針對全射流噴頭，利用MATLAB編程，對噴頭組合進行了三維插值模擬，編程相對簡單，組合效果易于三維展示[19-22]。嚴海軍等[23]根據Hunter和Rainbird公司分別提供的PGP型和R50型園林地埋式噴頭進行了不同組合系數的噴灑性能模擬試驗，發現在最大零漏噴范圍內，噴灌均勻系數的大小與組合形式關系不大，主要取決于噴頭結構及徑向水量分布曲線的特點。DEPIVOT是基于VB語言設計的評價指針式噴灌機軟件，可以計算線性均勻度及根據土壤入滲特性估算潛在徑流[24]，在指針式噴灌機設計及其性能評價上可參考應用。

綜上，當前大型噴灌機的噴頭噴灑組合效果，大部分通過CU、DU衡量。同時，噴頭的組合間距大部分通過桁架的長度和供水管輸水量決定噴頭的間距，國內常用噴頭組合間距以2.9 m居多。為此，本文針對當前噴灌機常用的Nelson噴頭R3000和O3000進行測量模擬多噴頭不同間距組合，對比噴灑組合模擬效果，并用MATLAB編程區分多噴頭組合全噴灑域與疊加域，分別分析全噴灑域與疊加域CU、DU和MSI，研究2種噴頭特性及其在大型噴灌機中使用的組合效果，為大型噴灌機系統的安裝設計提供了一種參考。

1 材料與方法

1.1 噴頭噴灑試驗系統

噴頭噴灑試驗系統主要有潛水泵、閥門、輸水管、渦輪流量計、壓力表、噴頭和雨量筒等。試驗在水利部節水灌溉設備質量檢測中心大廳進行，試驗程序和方法參照《美國農業工程師學會噴灌分布測試標準》[25]，試驗噴頭為Nelson R3000和O3000低壓旋轉噴頭。參考噴灌機噴頭高度，試驗噴頭距地面高度1.8 m。噴頭連接壓力調節器，試驗用22號噴嘴，內徑4.7 mm，噴頭正常工作壓力為0.1 kPa。雨量筒直徑10 cm，高15 cm，試驗在大廳內無風條件下進行。雨量筒以噴頭垂下地面位置為中心輻射徑向布置，布置8條輻射線，雨量筒間距為0.5 m。圖1噴頭試驗布置示意圖。

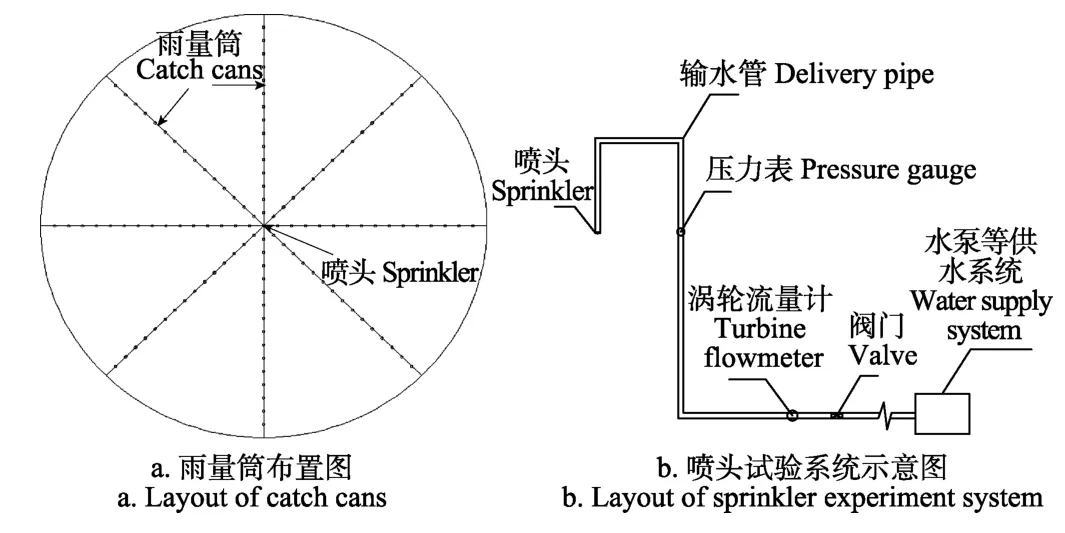
圖1 噴頭試驗系統及雨量筒布置示意圖Fig.1 Schematic of catch cans layout and sprinkler experiment system

1.2 均勻度計算

單噴頭和組合噴頭的均勻度計算，根據單噴頭和組合噴頭組合方式及其組合間距，選用克里斯琴森均勻度計算噴頭組合均勻度[13-14]，計算公式為

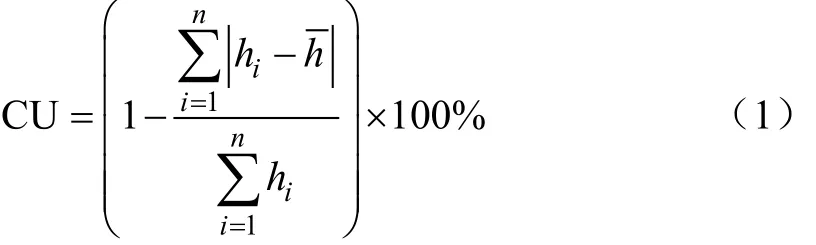
式中CU為克里斯琴森均勻度，%；hi為第i個測點的降水深，mm；h為噴灑面積上各測點平均降水深，mm；n為測點數目。

對于徑向布置的雨量筒噴灑試驗，需用不同計算方法將實測徑向降水深數據轉換為網格點的降水深，然后計算CU。一般是根據噴頭不同的組合方式和組合間距，通過二維插值，將單噴頭圓形噴灑域的水量分布試驗數據轉換為多噴頭組合的網格型數據，然后按照均勻度的計算方法求得多噴頭組合均勻度。

[14-15]計算DU：

式中ix為第i個測點的水深，mm。

如果田間絕大多數測點水深與平均值接近，個別測點水深與平均值偏差較大甚至為0（漏噴）時，CU難以反映這種情況，可用DU克服CU描述水量分布均勻性時的上述缺點，美國農業部推薦采用DU來描述水量分布的均勻性[15,18]。

1.3 模擬插值方法

噴頭組合后通過2次插值計算噴灑區域內任意一點P的降水深。如圖2所示，首先通過徑向插值分別計算出各輻射線上與點P距噴頭距離相同的Ai處的降水深hi（i=1,2,…8）。再利用同一圓周上的數據采用相同的插值法計算出所求網格點P的降水深。所用的插值方法主要為3次樣條插值，3次樣條插值是指通過一系列形值點的1條光滑曲線，在插值區間內滿足插值公式，最高次冪不高于3次的樣條函數。

圖2 數據點樣條插值示意圖Fig.2 Simulation interpolation schematic diagram

1.4 全噴灑域、疊加域和非疊加域區分

如果A點距離最近2個噴頭的距離小于等于噴頭的噴灑半徑，則A點屬于疊加域內的點，否則為非疊加域內的點。插值轉換成直角坐標系后，在坐標系內噴灑強度大于0的區域，為全噴灑域。

2 結果與分析

2.1 單噴頭噴灑特性

2.1.1 單噴頭噴灑域內噴灑水深DU和CU

對2種噴頭設置同樣的6組試驗：壓力50～300 kPa，步長50 kPa，結果如圖3所示。R3000噴頭CU均值為68.79%，DU均值50.82%，CU和DU的標準差（standard deviation，SD）分別為9.18%、8.18%。噴頭壓力在50～150 kPa間，CU、DU隨著壓力增大而增大；當壓力超過150 kPa后，隨著壓力增大，CU、DU逐漸下降；CU和DU變化趨勢一致，CU波動幅度較DU稍大。說明R3000在試驗中運行壓力為150 kPa時，噴灑效果最好（CU和DU分別為76.7%和62.0%）。O3000 噴頭CU均值為65.33%，DU均值55.69%，CU和DU的SD分別為3.65%、5.22%。噴頭壓力在50～200 kPa間，CU、DU隨著壓力增大而增大；當壓力超過200 kPa后，隨著壓力增大，CU、DU逐漸下降；CU和DU變化趨勢基本一致，DU變化幅度較CU大。說明O3000在試驗中壓力為200 kPa時，均勻性最好（CU和DU分別為69.8%和60.9%）。2個噴頭對比發現，在壓力50～300 kPa間，CU均值以R3000（68.79%）＞O3000（65.33%），R3000的噴灑均勻性好一點；而DU均值以R3000（50.82%）＜O3000（55.69%），說明空間分布均勻性O3000較R3000好。根據SD分析發現，壓力在50～300 kPa間時，O3000的CU和DU較R3000穩定。

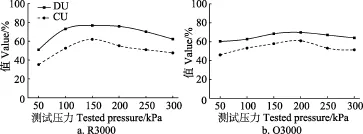
圖3 測試壓力下噴頭的分布均勻系數（DU）和組合均勻系數（CU）Fig.3 Christian uniformity coefficient (CU) and distribution uniformity coefficient (DU) of sprinklers with tested pressures

2.1.2 單噴頭水量分布

表1為2種噴頭在150 kPa下，至噴頭不同距離徑向布置雨量筒的實測降水深均值。采用MATLAB編程對噴頭噴灑強度進行插值，R3000和O3000噴頭的噴灑半徑分別為7.5和8 m。采用3次樣條插值，在無風條件下2個噴頭的水量分布情況如圖4所示。從表1降水深值和圖4噴灑強度均可看出，R3000噴頭水量在距噴頭2 m和4.5 m左右分布最多，O3000在噴頭周圍1 m內水量比較多，其次是在5～6.5 m范圍內分布較多。

表1 150 kPa壓力下至噴頭距離的降水深Table 1 Water depth at different distance to sprinkler under 150 kPa pressure mm

2.2 同類型2個噴頭組合噴灑特性

采用MATLAB插值后，將極坐標轉化到直角坐標系，找出噴水的部分，計算兩噴頭組合的CU、DU及平均噴灑強度（mean spraying intensity，MSI）。

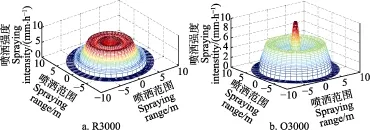
圖4 150 kPa壓力單噴頭水量分布Fig.4 Single sprinkler water distribution under 150 kPa pressure

圖5 a為兩R3000噴頭組合CU、DU和MSI，可看出，兩噴頭間距在1～8 m間，CU總體呈先降低后增高趨勢，拐點在兩噴頭間距為4.5 m的地方。組合后的最大值在兩噴頭間距為1 m時，CU為77%，4.5 m時CU最低，為63%。兩噴頭間距在1～5.5 m間，組合后DU小于60%，間距6～8 m DU超過60%。MSI隨著兩噴頭間間距增大，逐漸減小。圖5b為兩O3000噴頭組合后的CU、DU和MSI，可看出，兩噴頭間距在1～7 m間，CU總體呈逐漸減小趨勢，直到6.5 m處出現拐點，拐點后上升趨勢較平緩。組合后的最大值在兩噴頭間距為1 m時，CU為74%；4.5 m時CU最低66.8%。兩噴頭不同間距組合后DU呈現一定波動變化，波動范圍在54%～60%，間距2.5 m DU最小，為54%。MSI隨著兩噴頭間距增大，逐漸減小。圖6為兩噴頭1、3、7 m組合噴灑強度分布情況，隨著間距的變大，兩噴頭間的疊加部分在不斷的減少、噴灑范圍在逐漸增大。

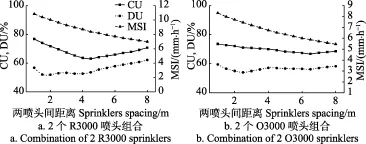
圖5 兩噴頭組合的均勻系數和平均噴灑強度（MSI）Fig.5 Uniformity coefficient and mean spraying intensity (MSI) of 2 sprinklers combinations

2.3 多噴頭組合噴灑特性

2.3.1 多噴頭組合全噴灑域情況

采用MATLAB插值后，將極坐標轉化到直角坐標系，找出噴水的部分，計算多噴頭組合CU、DU、MSI和噴灑范圍（spraying range，SR），如圖7所示。由圖7可知，R3000噴頭間距在1～6 m間，CU總體呈上升趨勢，6 m后略下降。組合后的最大值出現在兩噴頭6 m間距時，CU為68%；噴頭間距1 m時，CU最低51%。多噴頭組合DU隨著噴頭間距的增大，呈現逐漸上升趨勢，變化區間為28%～58%，間距6 m DU超過50%。多噴頭等間距組合情況下，SR與噴頭間距（x）呈線性相關，噴頭間距x∈[1～8] m，噴灑范圍SR∈[24～89] m。對MSI趨勢進行擬合得到，MSI與噴頭組合間距存在指數函數關系，x∈[1～7.5] m，在噴頭間距為3 m左右，MSI與SR 2條線有交叉，此點噴頭間距是當前平移式噴灌機常用噴頭組合間距。O3000多噴頭組合情況CU、DU、MSI、SR如圖7c～圖7d所示，可看出，噴頭間距在1～8 m間，CU、DU總體呈遞增趨勢，在5.5 m時CU略下降。CU、DU組合后的最大值都出現在噴頭7 m間距時，CU為72 %、DU為57%；噴頭間距1 m時，CU、DU最低，分別為55 %、31%。多噴頭等間距組合情況下，SR與x呈線性相關，x∈[1～8] m，SR∈[25～95] m。 對MSI趨勢進行擬合得到，MSI與噴頭組合間距存在指數函數關系x∈[1～8] m。在噴頭間距為3 m時，MSI與SR 2條線有交叉，此點噴頭間距是當前平移式噴灌機常用噴頭組合間距。圖8為多噴頭1、3、7 m組合噴灑強度分布情況，隨著間距的變大，多噴頭間的疊加部分在不斷的減少、噴灑范圍在逐漸增大。

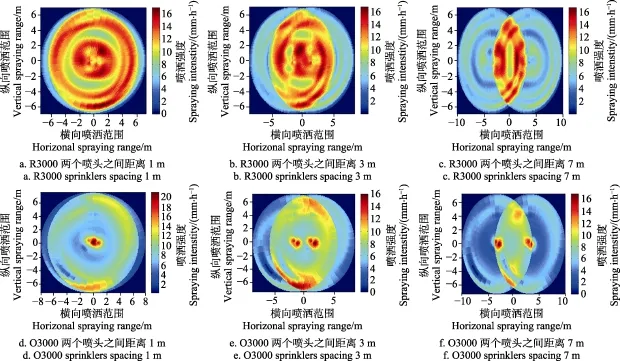
圖6 兩噴頭1、3、7 m組合噴灑強度分布Fig.6 Spraying intensity distribution of 2 sprinklers combination with spacing 1, 3 and 7 m

圖7 多噴頭組合均勻系數、平均噴灑強度及噴灑范圍(SR)Fig.7 Uniformity coefficient, MSI and spraying range (SR) of multiple sprinklers

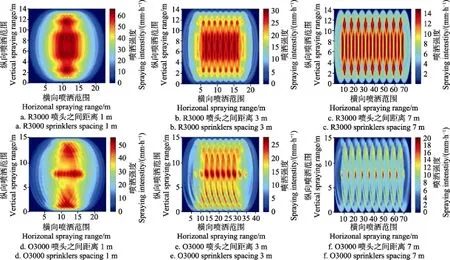
圖8 多噴頭1、3、7 m組合全噴灑域噴灑強度分布Fig.8 Spraying intensity distribution of multiple sprinklers combination with spacing 1, 3 and 7 m in whole spraying area

2.3.2 多噴頭組合疊加域情況

采用MATLAB提取噴頭噴灑疊加區域，得到R3000的多噴頭組合疊加域CU、DU和MSI，如圖9a所示。隨著噴頭間距不斷變大，CU、DU呈現逐漸增高趨勢。在噴頭間距為6 m時，CU達到噴灌工程規范中規定的行噴均勻度85%，DU為77%。噴頭間距在3.5 m后，DU超過65%。MSI隨著噴頭間距x的增大而減小，呈現指數函數關系：MSI=36.53 x-0.57（R2 = 0.993），x∈[1～7.5] m。提取疊加部分的MSI分布見圖10a～圖10c，隨著噴頭間距的變大，3個以上的噴頭噴灑重復疊加的區域逐漸減小。同時，整個噴灑范圍在不斷的增大。

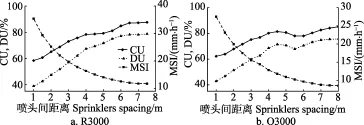
圖9 多噴頭組合疊加部分均勻系數和MSIFig.9 Uniformity intensity and MSI of many sprinklers combinations in overlap area

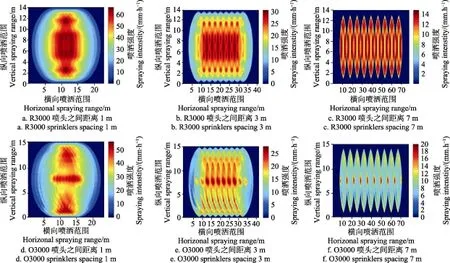
圖10 多噴頭1、3、7 m組合疊加部分噴灑強度分布Fig.10 Spraying intensity distribution of many sprinklers combinations with spacing 1, 3 and 7 m in overlap area

O3000的多噴頭組合疊加部分CU、DU和MSI如圖9b。噴頭間距在1～4.5 m內，組合間距變大，CU、DU呈現逐漸增高趨勢，4.5 m時出現1個峰，此時CU=81.4%，DU=71.4%。在噴頭間距為5.5 m時，CU、DU出現局部低值，分別為80%、67.8%。此后，噴頭間距增大，CU、DU逐漸增大。MSI隨著噴頭間距x的增大而減小，呈現MSI=29.42 x-0.6（R2 = 0.993），x∈[1～8 m]。提取疊加部分的噴灑強度分布見圖10d～圖10f，從圖中可以清晰地看出，O3000和R3000的疊加后疊加域的面積變化趨勢基本一致，但噴灑強度存在一定的差異，O3000噴灑強度比R3000噴灑強度分布更均勻些。

3 討 論

在MATLAB軟件中采用兩次插值的方法，得到單噴頭噴灑分布，插值的思路與前人研究[18,20,26-27]一致。多噴頭組合模擬數據采用室內試驗多條輻射線上的數據，非單獨1條線的數據，參考了Evans等做法[28]。結果發現，Nelson R3000和O3000噴頭在安裝壓力調節器條件下，測試壓力在50～300 kPa范圍內，R3000和O3000噴頭分別在壓力150和200 kPa時，CU、DU達到最優，這與鞏興暉[26]、Evans等[28]結論相近。本文發現，兩噴頭組合由于噴頭間距的調整導致噴頭的噴灑疊加范圍在不斷的變化，重合率隨著組合間距的變大而減小，兩噴頭組合均勻度出現“V”型變化趨勢。大型噴灌機用折射式噴頭兩兩組合無法體現其在噴灌機上的組合效果，需通過多噴頭組合展現噴灌機的噴頭組合特性。

多噴頭組合后發現，組合間距在1.9、2.9 m處，組合均勻度CU、DU并不最優，這也是印證了國內噴灌機的生產是根據桁架的長度和主管的管徑（輸水量）確定噴頭的組合間距。組合間距的不同均勻度亦不同[28]，當前主要測試和模擬大型噴灌機噴灑均勻度的方法為田間雨量筒測試法，經過加權計算出均勻度，以此為評價大型噴灌機的依據[24,29-31]。本文借鑒了這些研究方法，用多條輻射線上的點數據模擬單噴頭噴灑數據，以此為基礎疊加出多噴頭的組合噴灑情況。多噴頭組合均勻度的計算采用疊加后的數據計算得到，數據量大，涵蓋所有變化情況，與只通過測量噴灌機噴灑1條輻射線上的幾個點數據不同。本文組合后的均勻度值較他人[24,29]的研究計算值低，分析原因發現：1）本文程序插值計算的水深點密度太大，是常規測量CU、DU值所用數據點的數萬倍，數據點多涵蓋噴灑域全部變化情況，是導致計算的CU、DU值偏低的重要原因之一；2）本文采用的單噴頭數據為8條輻射線上點數據，而非旋轉式噴頭常采用1條輻射線的數據，實測8條輻射線數據有很大的差異性以及通過8條輻射線的數據計算得到單噴頭噴灑均勻性不高，也是導致模擬后計算多噴頭組合CU、DU值偏低的重要原因；3）本文模擬計算了噴灌機的靜態噴灑疊加，噴灑域內有的點有單噴頭噴灑點、兩噴頭疊加點、三噴頭疊加點和四噴頭噴灑疊加點，這些點數據存在很大的差異亦是出現CU、DU值偏低的原因之一；4）利用單噴頭數據組合疊加出多噴頭數據，與真實的噴灑疊加存在差異，真實噴頭水滴疊加存在相互碰撞、水滴再分布現象。

本文針對多噴頭組合的CU、DU和MSI的計算，進行了全噴灑域與疊加域的對比計算，發現疊加域的CU、DU和MSI值在相同噴頭間距時高于全噴灑域，這與事實相符。隨著噴頭間距不斷增大，全噴灑域面積有所增加，疊加域面積存在先變大后變小現象，還需要模擬計算進一步明確具體的變化過程，但MSI在全噴灑域和疊加域均不斷減小。現實測量評價大型噴灌機的CU、DU時，采取的雨量筒測量法，放置雨量筒的點都在噴頭疊加域內，只能反映靜態疊加域內幾個點值，無法完全反映整個噴灑域及其疊加域內情況。在未來的研究中，將進一步結合大型噴灌機的田間實測情況，考慮噴灌機的行走速率的變化，進一步分析模擬噴灌機的噴灑效果，以及考慮雨滴的大小與蒸散發的關系做更深一步研究。

4 結 論

該文應用試驗與插值方法研究噴灌機單噴頭、兩噴頭和多噴頭水分分布特性，結論如下：

1）單噴頭試驗中，在壓力50～300 kPa間，R3000和O3000 噴灑均勻度均值分別為68.79%和65.33%。根據標準差和分布均勻系數，O3000好于R3000。在150 kPa下，R3000噴頭水量在距噴頭2 m和4.5 m左右分布最多，而O3000在噴頭周圍1 m內水量比較多。

2）兩R3000噴頭間距在1～8 m間，CU呈先降低后增高趨勢，拐點在兩噴頭間距為4.5 m的地方。兩O3000噴頭間距在1～7 m間，CU總體呈逐漸減小趨勢，直到6.5 m處出現拐點。MSI隨著兩噴頭間距增大，逐漸減小。兩噴頭組合由于噴頭間距的調整導致噴頭的噴灑疊加范圍在不斷的變化，重合率隨著組合間距的變大而減小，兩噴頭組合均勻度出現“V”型變化趨勢。大型噴灌機用折射式噴頭兩兩組合無法體現其在噴灌機上的組合效果，需通過多噴頭組合展現噴灌機的噴頭組合特性。

3）多噴頭組合試驗表明，在噴頭間距為6 m時，R3000的CU達到噴灌工程規范中規定的行噴均勻度85%，DU為77%。隨著噴頭間距的變大，3個以上的噴頭噴灑重復疊加的區域在逐漸減小，同時，整個噴灑疊加區域在不斷的增大。O3000和R3000的疊加后疊加域的面積變化趨勢基本一致，但MSI存在一定的差異，O3000MSI分布均勻性上比R3000的更均勻些。比較疊加域和全噴灑域的CU、DU值，疊加域的值更高，現實測量噴灌機的噴灑均勻度用的雨量筒法測量的值，基本為疊加域中的值。全噴灑域計算出的CU、DU及MSI更能代表大型噴灌機的真實噴灑效果。

本文區分噴灌機的全噴灑域與疊加域，而計算得到的CU、DU值較其他研究偏低原因在于采用8條輻射線上的點數據插值疊加，而非常用的單條輻射線上的點數據插值疊加；疊加計算數據點多，涵蓋全部變化情況；此外，缺少了真實噴灑情境下不同噴頭噴灑水滴相互碰撞再分布的情況。

[參 考 文 獻]

[1] 中華人民共和國水利部編. 2016中國水利統計年鑒[M].北京:中國水利水電出版社，2016.

[2] 趙偉霞，李久生，栗巖峰. 大型噴灌機變量灌溉技術研究進展[J]. 農業工程學報，2016，32(13)：1-7. Zhao Weixia, Li Jiusheng, Li Yanfeng. Review on variable rate irrigation with continuously moving sprinkler machines[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(13): 1-7. (in Chinese with English abstract)

[3] 金宏智，何建強，錢一超. 變量技術在精準灌溉上的應用[J]. 節水灌溉，2003(1)：1-3. Jin Hongzhi, He Jianqiang, Qian Yichao. Application of VRT in precision irrigation[J]. Water Saving Irrigation, 2003(1): 1-3. (in Chinese with English abstract)

[4] 韓文霆，吳普特，馮浩，等. 方形噴灑域變量施水精確灌溉噴頭實現理論研究[J]. 干旱地區農業研究，2003(2)：105-107. Han Wenting, Wu Pute, Feng Hao, et al. Variable-rate sprinklers for precision irrigation on square area[J]. Agricultural Research in the Arid Areas, 2003(2): 105-107. (in Chinese with English abstract)

[5] Haghverdi A, Leib B G, Washington-Allen R A, et al. Perspectives on delineating management zones for variable rate irrigation[J]. Computers and Electronics in Agriculture, 2015, 117: 154-167.

[6] King B A, Wall R W, Kincaid D C, et al. Field testing of a variable rate sprinkler and control system for site-specific water and nutrient application[J]. Applied Engineering in Agriculture, 2005, 21(5): 847-853.

[7] Evans R G, LaRue J, Stone K C, et al. Adoption of sitespecific variable rate sprinkler irrigation systems[J]. Irrigation Science, 2013, 31: 871-887.

[8] O′Shaughness S A, Evett S R, Colaizzi P D, et al. Wireless sensor network effectively controls center pivot irrigation of sorghum[J]. Applied Engineering in Agriculture, 2013, 29(6): 853-864.

[9] Haghverdi A, Leib B G, Washington-Allen R A, et al. Studying uniform and variable rate center pivot irrigation strategies with the aid of site-specific water production functions[J]. Computers and Electronics in Agriculture, 2016, 123: 327-340.

[10] Sui R, Fisher D K. Field test of a center pivot irrigation system[J]. Applied Engineering in Agriculture, 2015, 31(1): 83-88.

[11] O’ Shaughness S A, Evett S R, Colaizzi P D. Dynamic prescription maps for site-specific variable rate irrigation of cotton[J]. Agriculture Water Management, 2015, 159: 123-138.

[12] King B A, Bjorneberg D L. Evaluation of potential runoff and erosion of four center pivot irrigation sprinklers[J]. Applied Engineering in Agriculture, 2011, 27(1): 75-85.

[13] 韓文霆，吳普特，楊青，等. 噴灌水量分布均勻性評價指標比較及研究進展[J]. 農業工程學報，2005，21(9)：172-177. Han Wenting, Wu Pute, Yang Qing, et al. Advances and comparisons of uniformity evaluation index of sprinkle irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(9): 172-177. (in Chinese with English abstract)

[14] 李久生，饒敏杰. 噴灌水量分布均勻性評價指標的試驗研究[J]. 農業工程學報，1999，15(4)：78-82. Li Jiusheng, Rao Minjie. Evaluation methods of sprinkler water nonuniformity[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1999, 15(4): 78-82. (in Chinese with English abstract)

[15] 韓文霆，王玄，孫瑜. 噴灌水量分布動態模擬與均勻性研究[J]. 農業機械學報，2014，45(11)：159-164，200. Han Wenting, Wang Xuan, Sun Yu. Dynamic simulation for sprinkler irrigation water distribution with uniformity[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(11): 159-164, 200. (in Chinese with English abstract) [16] Tarjuelo J M, Montero J, Honrubia F T, et al. Analysis of uniformity of sprinkle irrigation in a semi-arid area[J]. Agricultural Water Management, 1999, 40(2): 315-331.

[17] 韓文霆，崔利華，吳普特，等. 正三角形組合噴灌均勻度計算方法[J]. 農業機械學報，2013，44(4)：99-107. Han Wenting, Cui Lihua, Wu Pute, et al. Calculation methods for irrigation uniformity with sprinklers spaced in regular triangle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 99-107. (in Chinese with English abstract)

[18] 韓文霆，姚小敏，朱冰欽，等. 變量噴灑噴頭組合噴灌試驗[J]. 農業機械學報，2013，44(7)：121-126，112. Han Wenting, Yao Xiaomin, Zhu Bingqin, et al. test and evaluation on variable-rate irrigation sprinkler[J] Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(7): 121-126,112. (in Chinese with English abstract)

[19] 袁壽其，朱興業，李紅，等. 基于MATLAB全射流噴頭組合噴灌計算模擬[J]. 排灌機械，2008，26(1)：47-52. Yuan shouqi, Zhu Xingye, Li Hong, et al. Simulation of combined irrigation for complete fluidic sprinkler based on MATLAB[J]. Drainage and Irrigation Machinery, 2008, 26(1): 47-52. (in Chinese with English abstract)

[20] 朱興業，劉俊萍，袁壽其. 旋轉式射流噴頭結構參數及組合間距對噴灑均勻性的影響[J]. 農業工程學報，2013，29(6)：66-72. Zhu Xingye, Liu Junping, Yuan Shouqi. Effect on spraying uniformity based on geometrical parameters and combined spacing of rotational fluidic sprinkler[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(6): 66-72. (in Chinese with English abstract)

[21] Dwomoh F A, Shouqi Y, Hong L. Field performance characteristics of fluidic sprinkler[J]. Applied Engineering in Agriculture, 2013, 29(4): 529-536.

[22] Zhu X, Yuan S, Li H, et al. Irrigation uniformity with complete fluidic sprinkler in no-wind conditions[J]. Computer and Computing Technologies in Agriculture II, 2009, 2(295): 909-917.

[23] 嚴海軍，鄭耀泉. 兩種園林地埋式噴頭組合噴灑性能的模擬試驗[J]. 農業工程學報，2004，20(1)：84-86. Yan Haijun, Zheng Yaoquan. Simulating sprinkler performance of two combined pop-up sprinklers[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(1): 4-86. (in Chinese with English abstract)

[24] Valín M I, Cameira M R, Teodoro P R, et al. DEPIVOT: A model for center-pivot design and evaluation[J]. Computers and Electronics in Agriculture, 2012, 87: 159-170.

[25] ANSI/ASAE. Procedure for Sprinkler Distribution Testing for Research Purposes[M]. USA: ASAE S330, 2003.

[26] 鞏興暉. 移動式噴灌機折射式噴頭水量及動能分布規律研究[D]. 楊凌：西北農林科技大學，2015. Gong Xinghui, Study on the Water and Specific Power Distribution of the Spray-plate Sprinkler used in the Moving Sprinkler Machine[D].Yangling: Northwest A & F University, 2015. (in Chinese with English abstract)

[27] 李永沖，嚴海軍，徐成波，等.考慮水滴運動蒸發的噴灌水量分布模擬[J]. 農業機械學報，2013，44(7)：127-132. Li Yongchong,Yan Haijun, Xu Chengbo, et al. Simulation of sprinkler water distribution with droplet dynamics and evaporation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 44(7): 127-132. (in Chinese with English abstract)

[28] Evans R G, Han S, Kroeger M W. Spatial distribution and uniformity evaluations for chemigation with center pivots[J]. Transactions of the ASAE, 1995, 38(1): 85-92.

[29] Mohamed H, Abd El-wahed M M, Lorenzini G. Harvesting water in a center pivot irrigation system: Evaluation of distribution uniformity with varying operating parameters[J]. Journal of Engineering Thermoplastics, 2015, 24(2): 143-151.

[30] Moreno M A, Medina D, Ortega J F, et al. Optimal design of center pivot systems with water supplied from wells[J]. Agricultural Water Management, 2012, 107: 112-121.

[31] Ouazaa S, Latorre B, Burguete J, et al. Effect of the start-stop cycle of center-pivot towers on irrigation performance: Experiments and simulations[J]. Agricultural Water Management, 2015, 147: 163-174.

Static simulation on water distribution characteristics of overlap area and whole spraying area for sprinkler

Chen Zhen, Duan Fuyi, Fan Yongshen, JiaYanhui, Huang Xiuqiao※
(Farmland Irrigation Research Institute, CAAS, Henan Key Laboratory of Water-saving Agriculture, Xinxiang 453002, China)

This paper focused on water distribution characteristics of single, double and multiple sprinklers of large-scale lateral-moving sprinkler system. An experiment was carried out to measure Nelson R3000 and O3000 single sprinkler water distribution by catch cans. The catch cans were laid in the radiation lines in 8 directions. The spacing of 2 catch cans was 0.5 m along each line. The center point was a set of sprinkler, including a sprinkling system mounted 1.8 m high. A total of 6 pressures (from 50 kPa to 300 kPa) were applied in the process of measurement of a single sprinkler. Measurements included water depth, spraying radius, discharge and running time. The Christiansen uniformity (CU) and distribution uniformity (DU) of sprinklers were calculated. The superposition method with MATLAB was conducted to simulate water distribution of 2 sprinklers and multiple sprinklers by single sprinkler data. Meanwhile, CU, DU and mean spraying intensity (MSI) of 2 sprinklers and multiple sprinklers were obtained in MATLAB. Moreover, the overlap area (OA) and non-overlap area (NOA) were separated according to superposition principle and spraying spacing. The theory was that if one-point MSI was not 0, the point belonged to the whole spraying area. Meanwhile, the distances between the point and 2 of the sprinklers were less than spraying radius, which meant the point was in the OA. Otherwise, this point was in the NOA. The results showed the mean CU and DU of R3000 sprinkler were 68.79% and 50.82%. The CU and DU of R3000 sprinkler increased before the pressure of 150 kPa, indicating that the spraying effect was best at 150 kPa. The mean CU and DU of O3000 sprinkler were 65.33% and 55.69%. The CU and DU of R3000 sprinkler increased before the pressure of 200 kPa, indicating that the spraying effect was best at 200 kPa. The standard deviation of the uniformity showed that the O3000 was more stable than the R3000 at the pressure of 50-300 kPa. The water depth distribution and spraying intensity distribution at 150 kPa away from the sprinkler and showed that the R3000 had the highest water depth at about 2 and 4.5 m away from the sprinkler and the O3000 had the highest water depth at about 5-6.5 m away from the sprinkler. The spraying radius of R3000 and O3000 was 7.5 and 8.0 m, respectively. For the 2 R3000 sprinklers combinations, the CU decreased with the spacing of the 2 sprinklers increased to 4.5 m, the DU was smaller than 60% when the spacing between the 2 sprinklers was 1-5.5 m, and the mean spraying intensity (MSI) decreased with the spacing increased. For the 2 O3000 sprinklers combinations, the CU decreased with the spacing of the 2 sprinklers increased to 6.5 m, the DU was about 54%-60% when the spacing between the 2 sprinklers was 1-8 m, and the MSI decreased with the spacing increased. The overlap area of the 2 sprinklers decreased but the spraying range increased with the spacing increased from 1 to 7 m. For the multiple R3000 sprinklers combinations, the CU increased when the spacing was increased from 1 m to 6 m and the maximum CU was 68% at the spacing of 6 m, and the DU increased when the spacing increased and its value was above 50% at the spacing of 6 m. For the multiple O3000 sprinklers combinations, the CU and DU were highest with 72% and 57%, respectively at the spacing of 7 m, and were lowest with 55% and 31% at the spacing of 1 m. The CU and DU in the overlap area was higher than the whole spraying area but the CU was still lower than 85%. The study provides valuable information for the design of the sprinkler system.

sprinklers; uniformity; pressure; Nelson R3000; O3000; superposition method; sprinkling model

10.11975/j.issn.1002-6819.2017.16.014

S275.5；S277.9+4

A

1002-6819(2017)-16-0104-08

陳 震，段福義，范永申，賈艷輝，黃修橋. 噴灌機全噴灑域與疊加域水量分布特性的靜態模擬[J]. 農業工程學報，2017，33(16)：104-111.

10.11975/j.issn.1002-6819.2017.16.014 http://www.tcsae.org

Chen Zhen, Duan Fuyi, Fan Yongshen, JiaYanhui, Huang Xiuqiao. Static simulation on water distribution characteristics of overlap area and whole spraying area for sprinkler[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(16): 104-111. (in Chinese with English abstract)

doi：10.11975/j.issn.1002-6819.2017.16.014 http://www.tcsae.org

2017-02-13

2017-06-10

國家重點研發計劃（2016YFC0400104）；中央級科研院所基本科研業務費專項（中國農業科學院農田灌溉研究所）

陳 震，男，博士生，助理研究員，主要從事噴灌技術研究。新鄉中國農業科學院農田灌溉研究所，453002。Email：chenzhen@caas.cn

※通信作者：黃修橋，男，研究員，博士生導師，主要從事節水高效灌溉技術與裝備研究。新鄉 中國農業科學院農田灌溉研究所，453002。Email：huangxq626@126.com