關于不定方程x2+4n=y13(n=4,5,6)的整數解
尚旭
(浙江師范大學數理與信息工程學院,浙江 金華 321004)
關于不定方程x2+4n=y13(n=4,5,6)的整數解
尚旭
(浙江師范大學數理與信息工程學院,浙江 金華 321004)
在高斯整環中,利用代數數論與同余理論的方法,討論了不定方程
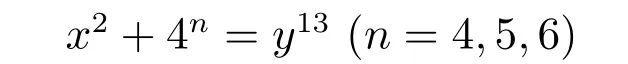
的整數解問題,得出了當n=4,5時無整數解;n=6是僅有整數解

的結論,推進了不定方程整數解的研究.
代數數論;整數解;不定方程
1 引言
設A、B∈N,A無平方因子,關于不定方程
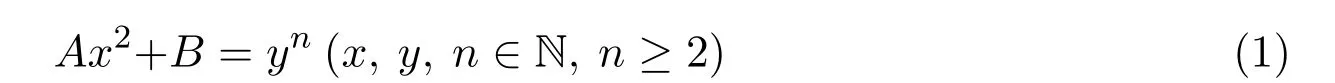
解的問題是數論中的一個重要問題,近些年文獻 [1-10]用代數數論的方法研究了一些不定方程的整數解問題,得到了許多重要的結果,推進了不定方程整數解問題的研究.而對于A=1,B=44,45,46,n=13情況為曾說明,為此利用代數數論和同余的方法給出不定方程x2+4n=y13(n=4,5,6)整數解的結論和證明.
引理 1.1[11]設M 是惟一分解整數環,正整數k≥2,以及 α,β∈Z,(α,β)=1,αβ=τk,τ∈M則有
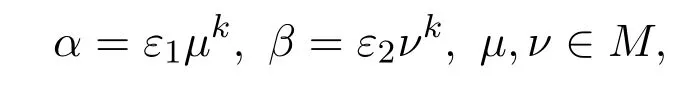
其中ε1,ε2是M 中的單位元素,并且
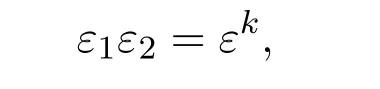
ε為單位元素.
2 主要結果與證明
定理2.1不定方程

無整數解.
證明分兩種情況來討論.
(1)當x≡1(mod 2)時,則在Z[i]中,(2)可以等價為

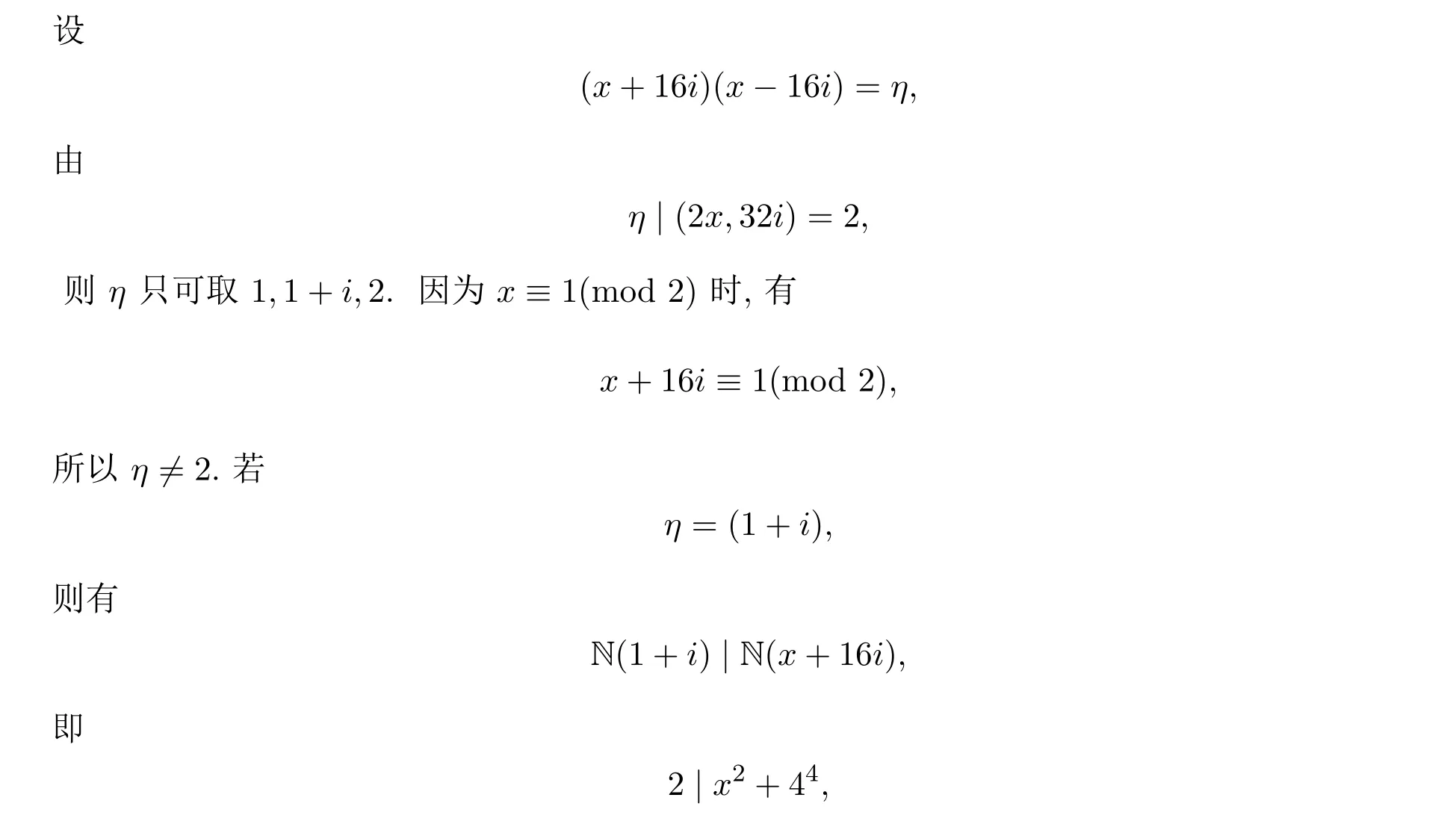
然而這與x≡1(mod 2)產生矛盾,所以η=1.
由此和引理1.1有
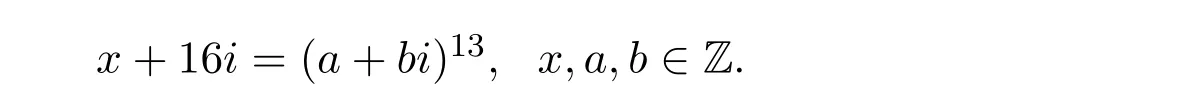
因而
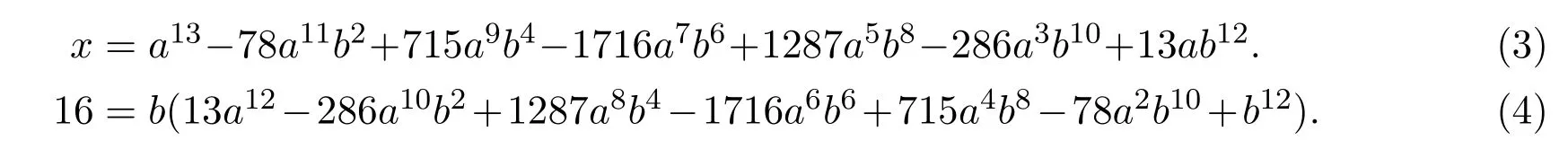
由 (4)式得

當 b=1時,由 (4)式,得
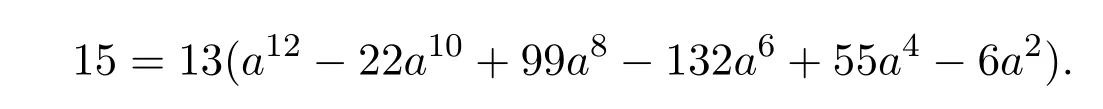
當 b=-1時,由 (4)式,得
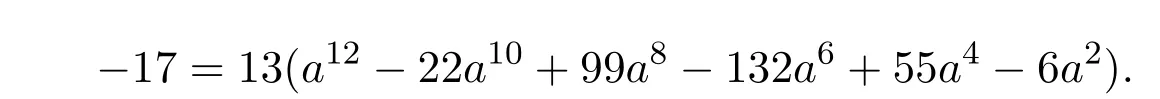
當 b=2時,由 (4)式,得
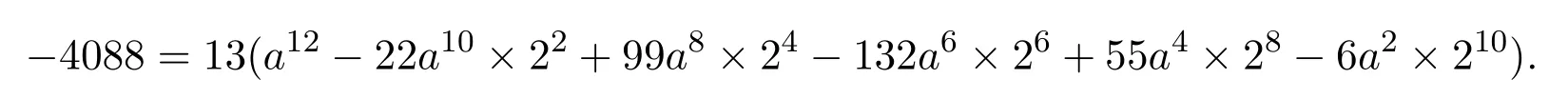
上式要成立,需

顯然不可能,故當b=2時不成立.
當 b=-2時,由 (4)式,得

上式要成立,需13|-4104,顯然不可能,故當b=-2時不成立.
當 b=4時,由 (4)式,得
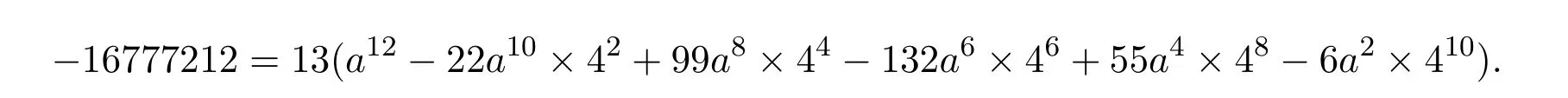
上式要成立,需

顯然不可能,故當b=4時不成立.
當 b=-4時,由 (4)式,得
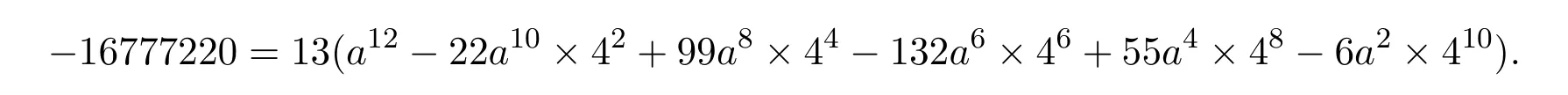
上式要成立,需
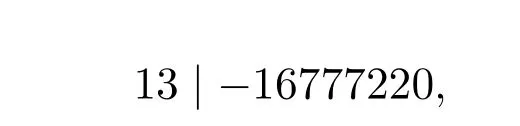
顯然不可能,故當b=-4時不成立.
當 b=8時,由 (4)式,得
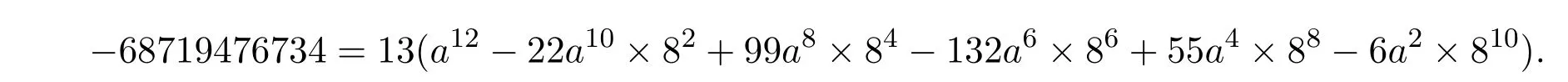
上式要成立,需
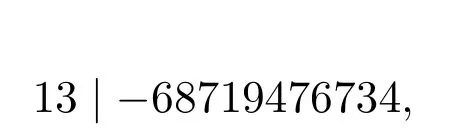
顯然不可能,故當b=8時不成立.
當 b=-8時,由 (4)式,得

上式要成立,需

顯然不可能,故當b=-8時不成立.
當 b=16時,由 (4)式,得
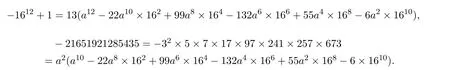
上式要成立,則
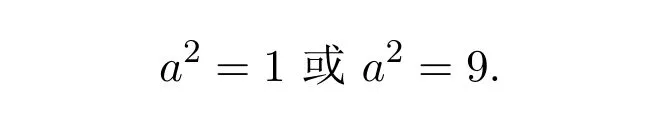
當a2=1時,代入上式中得
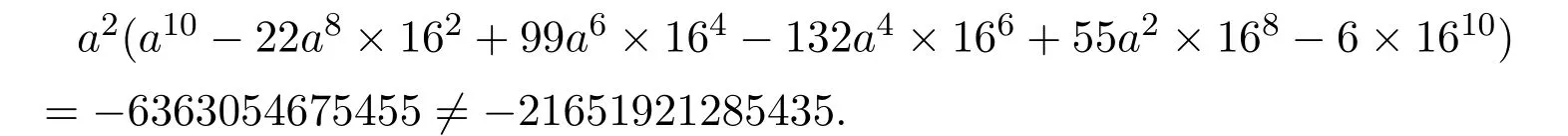
所以a2=1不成立.
當a2=9,代入上式中得

所以a2=9不成立.故當b=16時不成立.
當 b=-16時,由 (4)式,得
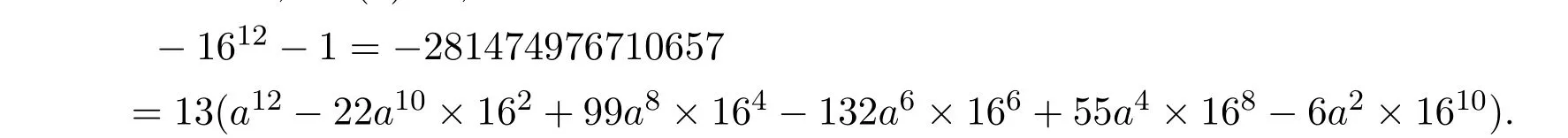
上式要成立,需

顯然不可能,故當b=-16時不成立.所以當x≡1(mod 2)時,不定方程

無整數解.
(2)當x≡0(mod 2)時,易知x為偶數,y為偶數,令

無整數解.
綜上所述,不定方程(2)無整數解.
定理2.2不定方程

無整數解.
證明分兩種情況來討論.
(1)當x≡1(mod 2)時,則在Z[i]中,(10)可以等價為
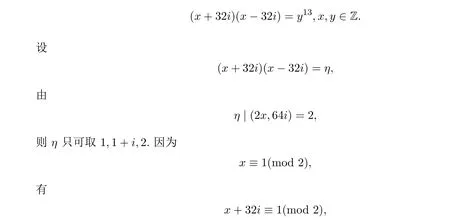



將其代入(15)式中得(2x4)2+42=27(y1)13.得

易知x4為偶數,令 x4=2x5,x5∈Z.將其代入(16)式中得(2x5)2+4=25(y1)13.得

易知x5為奇數,令 x5=2x6+1,x6∈Z.將其代入 (17)式中得(2x6+1)2+1=23(y1)13.得

(18)式等號左邊2(x6)2+2x6+1≡1(mod 2),而右邊22(y1)13≡0(mod 2),所以產生矛盾.所以當x≡0(mod 2)時,不定方程x2+45=y13無整數解.
綜上所述,不定方程(10)無整數解.
定理2.3不定方程

僅有整數解(x,y)=(±64,2).
證明分兩種情況來討論.
(1)當x≡1(mod 2)時,則在Z[i]中,(19)可以等價為

即2|x2+46,然而這與x≡1(mod 2)產生矛盾,所以η=1.
由此和引理1.1有
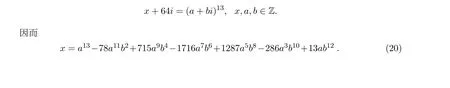
64=b(13a12-286a10b2+1287a8b4-1716a6b6+715a4b8-78a2b10+b12). (21)由 (4)式得
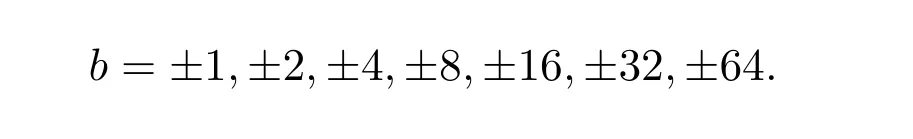
當 b=1時,由(21)式得
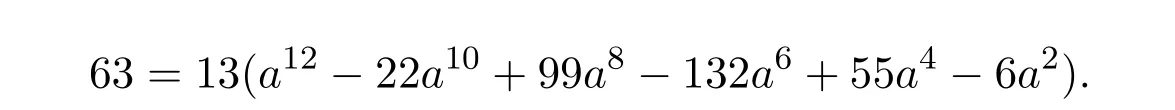
當 b=-1時,由(21)式得

上式要成立,則a2=1.將a2=1代入上式得
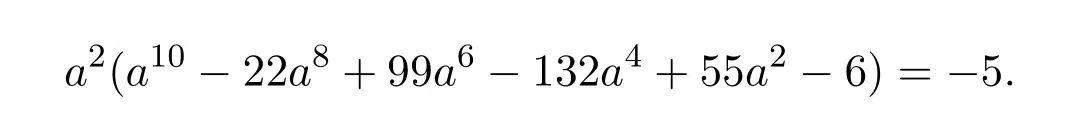
上式成立,則

將 a2=1,b=-1代入 (20)式解得x=±64,然而這與x≡1(mod 2)矛盾,故不成立.故當b=-1時不成立.
當 b=2時,由(21)式得
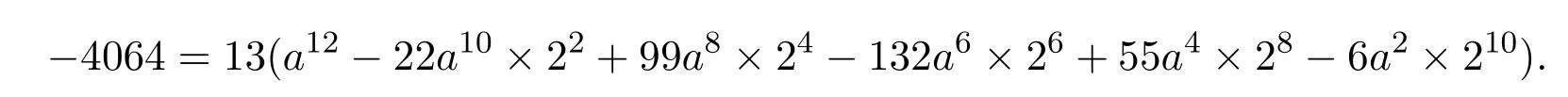
上式要成立,需13|-4064,顯然不可能,故當b=2時不成立.
當 b=-2時,由(21)式得

上式要成立,需

顯然不可能,故當b=-2時不成立.
當 b=4時,由(21)式得
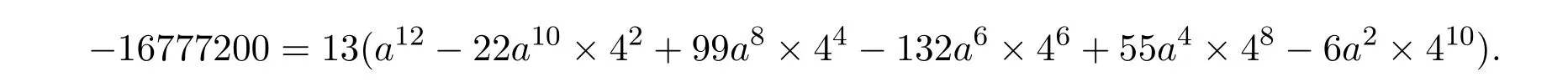
上式要成立,需

顯然不可能,故當b=4時不成立.
當b=-4時,由(21)式得

上式要成立,需
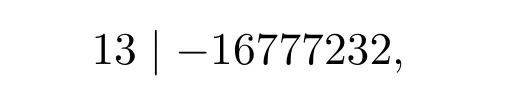
顯然不可能,故當b=-4時不成立.
當b=8時,由(21)式得
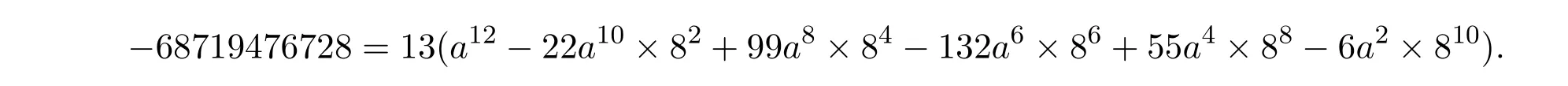
上式要成立,需
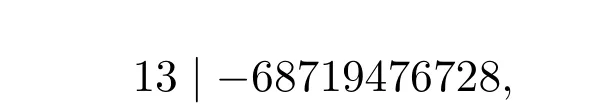
顯然不可能,故當b=8時不成立.
當b=-8時,由(21)式得
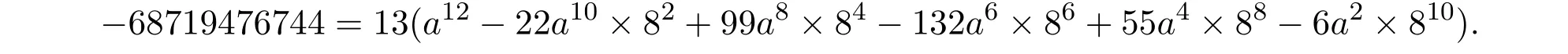
上式要成立,需

顯然不可能,故當b=-8時不成立.
當b=16時,由(21)式得

上式要成立,需
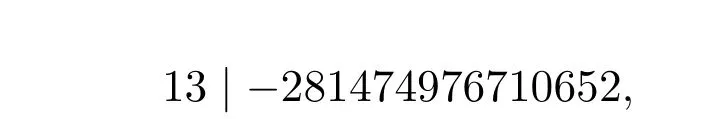
顯然不可能,故當b=16時不成立.
當b=-16時,由(21)式得
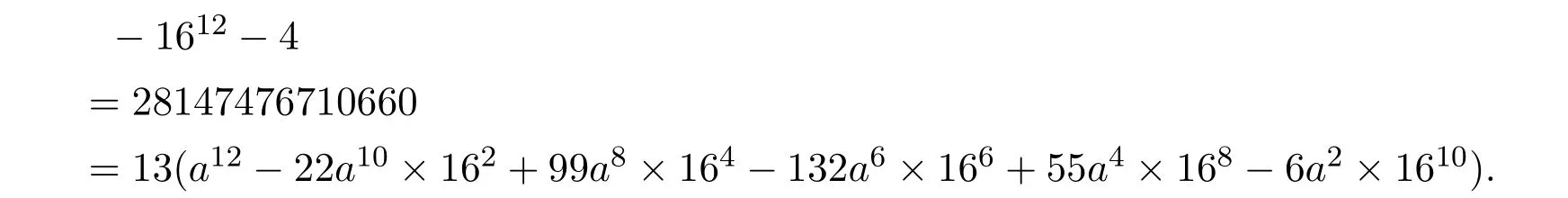
上式要成立,需

顯然不可能,故當b=-16時不成立.
當b=32時,由(21)式得
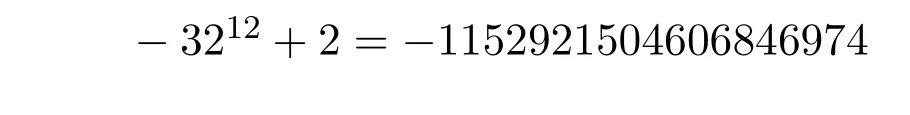
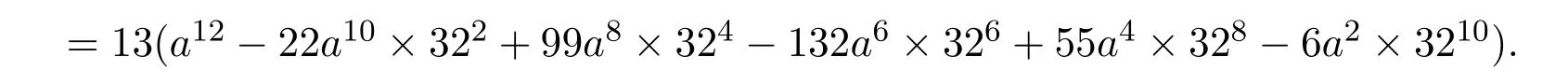
上式要成立,需

顯然不可能,故當b=32時不成立.
當b=-32時,由(21)式得
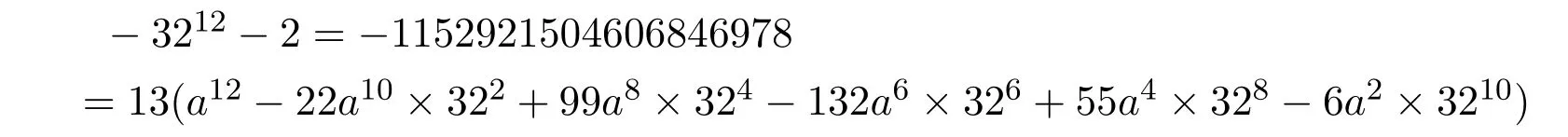
上式要成立,需
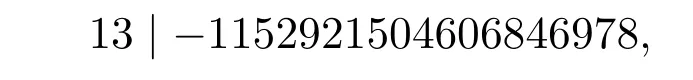
顯然不可能,故當b=-32時不成立.
當b=64時,由(21)式得

上式要成立,則
當a2=1時,代入上式中得

所以a2=1時不成立.當a2=9時,代入上式中得

所以a2=9時不成立.故當b=64時不成立.
當 b=-64時,由(21)式得

上式要成立,需

顯然不可能,故當b=-64時不成立.所以當x≡1(mod 2)時,不定方程

無整數解.


3 結語
不定方程的整數解問題是一個悠久的研究課題,許多數學家都有所研究,推進了不定方程整數解問題的發展,本文研究了x2+4n=y13(n=4,5,6)的整數解問題,得出了不定方程x2+4n=y13,當n=4,5時無整數解,當n=6時僅有整數解(x,y)=(±64,2)的結論和證明,接下來希望可以進一步研究不定方程的整數解問題.
[1]Lebesgue V A.Surlimpossibilite en number entiers de equation xm=y2+1[J].Nouvelle Annals of Mathematics,1850,9(1):178-181.
[2]Nagell T.Surlimpossibilite de quelques equations deux indeterminees[J].Norsk Marem Fornmings Skrefter Senel,1921,13(1):65-82.
[3]孫樹東.不定方程x2+64=y13的整數解[J].吉林師范大學學報:自然科學版,2015,(3):78-80.
[4]楊全.關于不定方程x2+16=y9的解[J].牡丹江大學學報,2013,22(8):119-120.
[5]李中恢,張四保.關于不定方程x2+16=y11的解[J].海南大學學報:自然科學版,2009,27(3):216-218.
[6]張杰.關于不定方程x2+64=y7的解的討論[J].慶工商大學:自然科學版,2012,29(3):27-28.
[7]安曉峰.關于不定方程x2+64=y11的解的討論[J].慶工商大學:自然科學版,2014,31(10):16-17.
[8]張四保.關于不定方程x2+16=y13的解[J].華大學學報:自然科學版,2009,10(4):307-309.
[9]唐維彬.關于不定方程x2+4n=y11[J].重慶工商大學:自然科學版,2015,32(1):15-18.
[10]常茸茸,魯志娟.關于丟番圖方程xp?1=Dyn[J].純粹數學與應用數學,2008,24(1):140-143.
[11]潘承洞,潘承彪.代數數論[M].2版.哈爾濱:哈爾濱工業大學出版社,2014.
The integer solution on Diophantine equation x2+4n=y13(n=4,5,6)
Shang Xu
(College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua 321004,China)
In the Gauss domain,using the method of algebraic number theory and congruence theory,we discuss the problem of integer solution of Diophantine equation x2+4n=y13(n=4,5,6).We obtained when n=4,5,x2+4n=y13has no integer solution,when n=6,x2+4n=y13has only integer solution(x,y)=(±64,2),which advanced the study of Diophantine equation.
algebraic number theory,integer solution,Diophantine eqution
O156;O156.2
A
1008-5513(2017)04-0377-15
10.3969/j.issn.1008-5513.2017.04.006
2017-05-01.
國家自然科學基金(11171137);浙江省自然科學基金(LY13A010008).
尚旭(1989-),碩士生,研究方向:初等數論與算子代數.
2010 MSC:11D45

