力控法蘭的模糊PID恒力控制方法*

黃 婷，孫立寧，王振華，禹鑫燚，陳國棟

(1．蘇州大學機器人與微系統研究中心 蘇州，215021)(2.浙江工業大學信息工程學院 杭州，310023)

力控法蘭的模糊PID恒力控制方法*

黃 婷1，孫立寧1，王振華1，禹鑫燚2，陳國棟1

(1．蘇州大學機器人與微系統研究中心 蘇州，215021)(2.浙江工業大學信息工程學院 杭州，310023)

針對工業機器人進行接觸式作業過程中對末端接觸力的要求，提出了一種基于力控法蘭的末端恒力控制方法。對力控法蘭進行了分析建模與參數辨識，設計了模糊控制與比例積分微分(proportion integral derivative,簡稱PID)控制并行的模糊PID控制器，通過Matlab仿真對純模糊控制與模糊PID控制效果進行了對比，并研究了模糊PID控制器各參數對控制性能的影響。最后，搭建了基于Labview和外部設備互連(peripheral component interconnect,簡稱PCI)總線數據采集卡的實驗平臺，對力控法蘭末端輸出力進行了實驗驗證。仿真結果表明，純模糊控制可提高系統響應性能，但存在一定的穩態誤差。加入PID控制與模糊控制并行控制后，仿真與實驗證明，階躍響應的穩態誤差消除，正弦跟隨效果明顯改善，恒力控制輸出力在期望力F=10 N時波動誤差為±0.8 N。因此，通過模糊PID控制可實現力控法蘭末端的恒力控制，具有較好的動態響應性和跟隨魯棒性。

力控法蘭；恒力控制；實驗測定法；模糊PID控制

引 言

隨著工業機器人的快速發展，其在各工業領域的應用越來越廣泛[1]。一些接觸式作業場合，要求工業機器人具有對接觸力的感知與控制能力，以達到精密操作的要求，例如，磨削、拋光和裝配作業等[2-3]。在進行磨拋作業時，加工工具隨著使用而發生磨損，產生表面位置誤差[4]，使接觸力發生變化，進而影響加工效果。因此，實現工具與工件的恒力接觸對工業機器人在接觸式作業中的應用有著重要的實踐意義。

目前，實現接觸力控制的方式主要有主動力控制和被動力控制兩種[5]。主動力控制由機器人控制器實現，一般采用力/位混合控制的方法[6-8]。由于該方法需要同時實現力和位置的控制，存在力/位耦合，因而實現較為復雜。相比較而言，被動力控制引入獨立于機器人的柔性裝置，將力控制從機器人控制器分離出來，通過柔性裝置實現，比主動力控制簡單易行，因此在工業應用場合有更廣泛的應用前景。文獻[9]提出了遠中心柔順手腕(remote center compliance,簡稱RCC)用于裝配作業,能對任意柔順中心進行順從運動。由于RCC裝置的柔順中心一旦確定，就很難調整，因而通用性較差。文獻[10]給機器人研磨和拋光系統的研拋砂帶增加了柔順機構，在接觸后能夠自適應改變研磨接觸力,代替了人工研磨渦輪機葉片。文獻[11]基于氣囊拋光加工技術分析了下壓深度和充氣壓力對接觸力的影響，采用BP神經網絡PID控制策略進行拋光接觸力控制，獲得了較好的加工效果。

筆者在以上研究的基礎上，引入一種力控法蘭裝置。該裝置可被動上下調節以適應機器人和工件之間的距離，伺服閥根據控制信號對氣缸內的氣壓進行調節，使位移被動發生變化的過程中接觸力保持恒定，從而實現末端恒力控制。對力控法蘭進行建模，設計一種模糊PID控制器，以改善其末端輸出力的動態性能和魯棒性。

1 力控法蘭建模

力控法蘭裝置模型圖和樣機如圖1所示，該裝置主要包括法蘭接口、上基座、導向機構、下基座、伺服閥、氣缸以及位移傳感器。其工作原理如下：首先，給伺服閥預設一個氣壓值，使氣缸對基座和機械接口產生一定張力。導向機構約束上下基座只能在一個方向相對移動，當工具與工件接觸產生接觸力，使得上下兩端壓縮，壓力傳感器反饋氣缸腔內氣壓值。當接觸力偏小時，伺服閥進氣口打開向氣缸腔內進氣以增加壓力；當接觸力偏大，氣缸腔內的氣壓超過設定氣壓時，伺服閥排氣口打開，通過氣管向外排氣以減小壓力。在平衡狀態下，依靠伺服閥維持氣缸腔內的壓力保持不變，從而使輸出力保持恒定。根據裝置結構，綜合考慮伺服閥流量方程、氣缸質量流量連續性方程及系統的力平衡方程，對力控法蘭進行分析與建模。

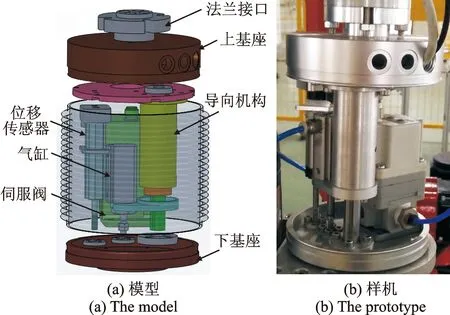
圖1 力控法蘭裝置Fig.1 Force-controlled flange device

1.1 力控法蘭流量模型

力控法蘭氣體流通原理圖如圖2所示。法蘭的輸入信號為控制電壓u，輸出為力Fn。根據輸入的控制電壓u，控制伺服閥輸出氣壓至低摩擦氣缸。伺服閥和氣缸之間采用氣管連接(圖2中虛線表示氣管連接)，氣壓作用于氣缸，產生輸出力Fn。

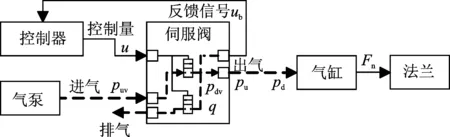
圖2 力控法蘭氣體流通原理圖Fig.2 Schematic diagram of gas flow in force-controlled flange

伺服閥供氣口通過的流量與供氣口壓強、出氣口壓強和閥口開度有關。采用Sanvile流量公式有

(1)

其中：q為通過閥口的流量；Puv為供氣口的壓強；Pdv為出氣口的壓強；Av為閥口的有效面積；k為絕熱系數；Cf為伺服閥節流口流量參數；T為絕對溫度；Rc為理想氣體常數。

在實際拋磨中，一般所需接觸力較小，故出氣口氣壓通常較小，式(1)中的第1式成立。此時，假設供氣口壓強和伺服閥內氣體溫度一定，則閥口流量僅與閥口有效面積有關，而閥口有效面積與伺服閥控制電壓有關，其影響的是出氣口的壓強，因此可以認為流量公式是與控制電壓u及閥出氣口壓強Pdv有關的函數。將其在零位附近線性化，得到伺服閥的流量增量模型為

Δq=K1Δu+K2ΔPdv

(2)

伺服閥輸出的氣流經過一段長度為L的氣管，進入氣缸的上腔。氣管中氣體流量等于伺服閥出口流量。根據Anderson理論，有

q=K3(Pu-Pd)

(3)

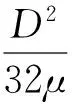
根據式(3)得到氣管內氣體流量增量模型

Δq=K3(ΔPu-ΔPd)

(4)

氣體經過伺服閥和氣管進入氣缸。假設氣缸內的氣體為理想氣體，滿足理想氣體狀態方程，則有

Pd=ρdRcTd

(5)

其中：Pd為氣缸腔內的氣體壓強；ρd為腔內氣體密度；Td為腔內氣體的熱力學溫度。

假設氣體流通過程中溫度滿足絕熱過程，根據質量流量q等于該腔內氣體質量m的變化率。結合式(5)推導可得氣缸腔內流量模型為

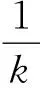
(6)

分別將式(2)，(4)和(6)進行Laplace變換，有

Q(s)=K1U(s)+K2Pdv(s)

(7)

Q(s)=K3Pu(s)-K3Pd(s)

(8)

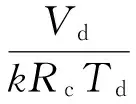
(9)

氣管進氣口壓強Pu即伺服閥出氣口壓強Pdv，即Pdv(s)=Pu(s)。聯立式(7)～(9)可得

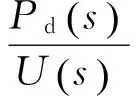
(10)

因此，根據對力控法蘭各部分的流量進行建模分析，得到裝置從輸入的伺服閥控制電壓到氣缸內輸出壓強的關系模型，如式(10)所示。

1.2 力控法蘭力平衡方程

腔內壓強Pd作用于氣缸，氣缸受力面積為Ad。對力控法蘭進行受力分析，如圖3所示。

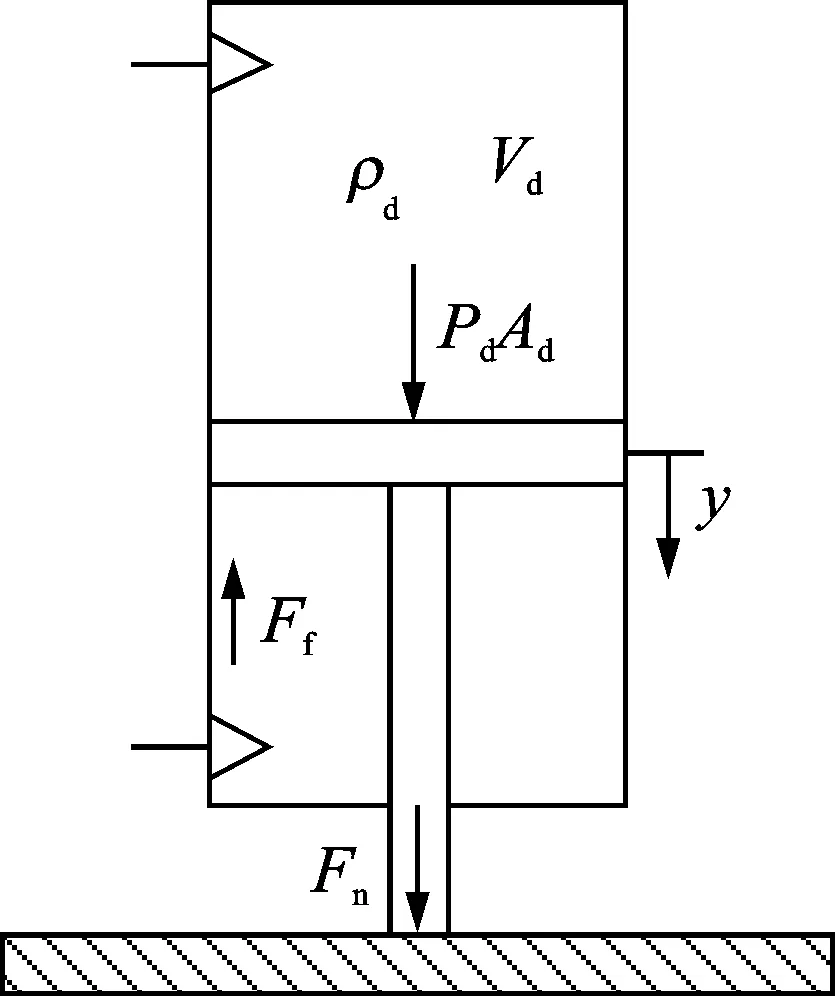
圖3 力控法蘭受力分析Fig.3 Force analysis of force-controlled flange

根據牛頓第二定律，有

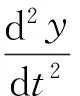
(11)

其中：Fn為力控法蘭輸出力；Ff為摩擦力；M為氣缸連接部件的總質量；Cp為黏性阻尼系數；y為氣缸活塞運動的位移。

忽略低摩擦氣缸的摩擦力，對式(11)進行拉普拉斯變換，有

(12)

末端工具與工件接觸，作用力Fn使力控法蘭被動產生位移y。等效剛度系數為Ke，則有

Fn(s)=KeY(s)

(13)

聯立式(12)和(13)可得

（一）在主推品種方面 武隆縣在肉牛產業發展中，主推西門塔爾牛和安格斯牛，首先用西門塔爾牛冷凍精液配種川南山地黃牛經產母牛，再用安格斯牛凍精配種“西雜牛”，并將“紅西本”三雜牛作為商品牛進行育肥出售。

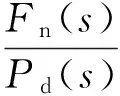
(14)

綜合式(10)，式(12)～(14)，裝置的傳遞函數框圖如圖4所示。

圖4 力控法蘭開環系統傳遞函數框圖Fig.4 Open-loop system transfer function diagram of force-controlled flange

結合式(10)與式(14)，系統的開環傳遞函數可表示為

G(s)=

(15)

得到力控法蘭的輸入控制量與輸出拋磨力之間的模型如式(15)所示。可見，該系統是一個三階系統。由于該模型中存在許多非線性影響因素，無法對其進行準確量化。為了對系統進行控制，可以將其作為一個“黑盒子”進行參數辨識。

2 力控法蘭模型測定

數學模型實驗測定是通過給系統施加特定的信號，采集響應輸出信號隨時間變化的曲線進行分析，從而實現對模型參數的辨識。主要方法有時域測定法、頻域測定法和統計相關測定法。筆者采用相對簡單易行的時域測定法。為了提高實驗測定模型的精度，采用有延遲的n階慣性環節進行擬合。表達式為

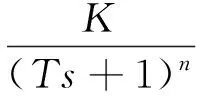
(16)

在t=0時，施加階躍輸入控制電壓u，力控法蘭輸出力F隨時間變化的響應曲線如圖5所示。

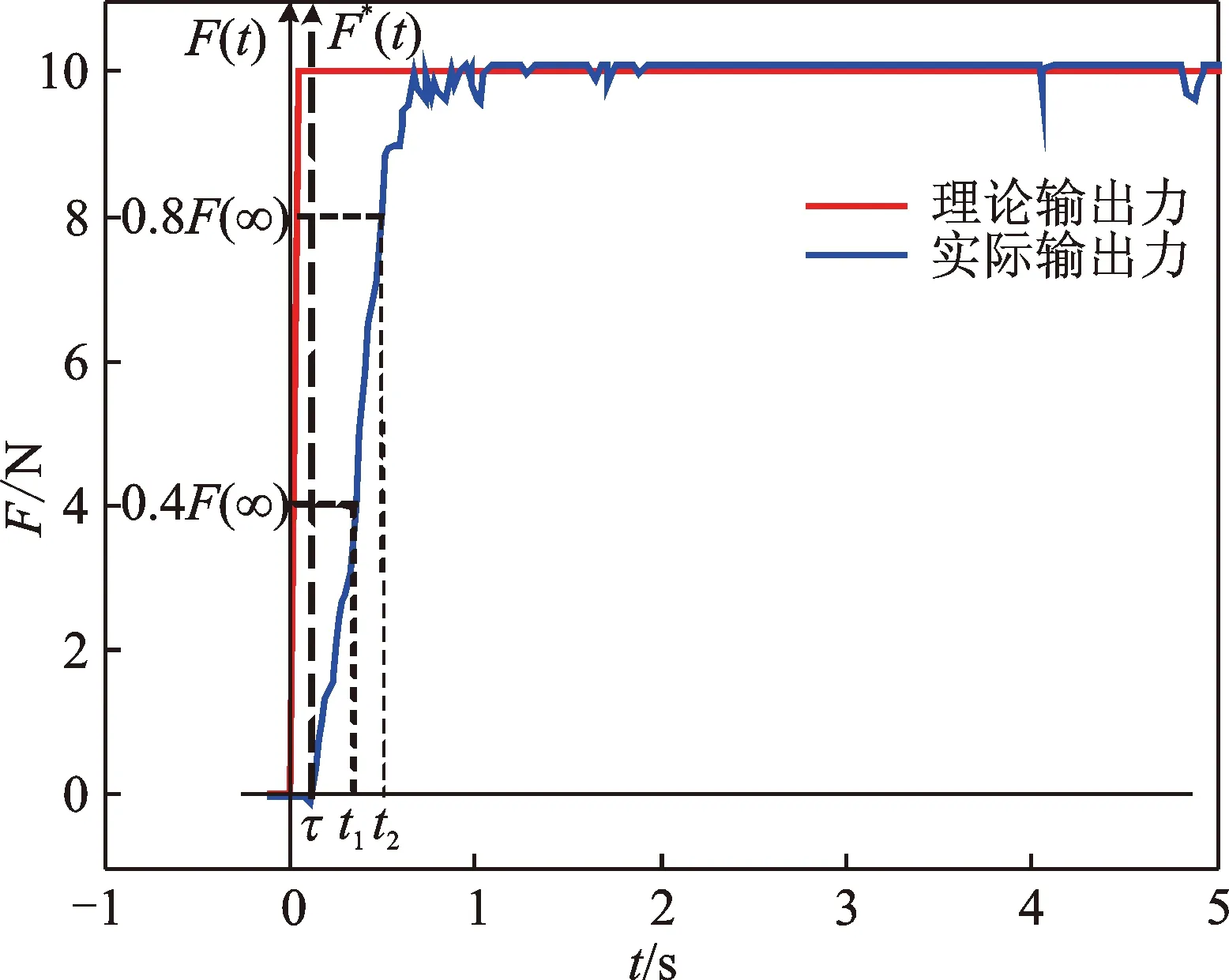
圖5 有延遲的n階擬合兩點法Fig.5 N order fitting two-point method with delay

2.1 參數確定

2.1.1 增益K

如圖5所示，設給定階躍輸入幅值為u，其增益K可按下式求取

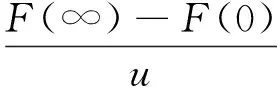
(17)

將u=0.759 2 V,F(0)=0,F(∞)=10.11N代入式(17)，得到K=13.316 6。

2.1.2 延遲時間τ

響應曲線延遲時間τ根據階躍響應曲線開始出現變化的時刻來確定。如圖5所示，在t=0時施加輸入信號，t=0.078 s時輸出信號響應曲線開始發生變化，因此τ=0.078 s。

2.1.3 階次n和時間常數T

計算階次n的近似公式為

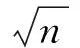
(18)

將計算結果取整，得到階次n=5。

時間常數為

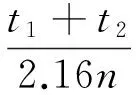
(19)

代入參數，計算得到T=0.059 4 s。

因此，實驗測定力控法蘭模型為

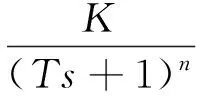
(20)

2.2 模型簡化

由于時間常數T=0.059 4 s，分母部分展開后其高階部分系數遠小于1，對系統影響較小，可近似忽略。因此，忽略系統的高階項，得到模型為

(21)

由拉氏變換延遲定理可知，延遲環節的傳遞函數可表示為

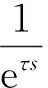
(22)

將eτs按泰勒級數展開，得到

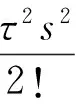
(23)

由于τ很小，忽略高階項，取其前兩項，eτs=1+τs，于是有

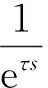
(24)

式(24)表明，在延遲時間很小的情況下，延遲環節可用一個小慣性環節來代替。

得到力控法蘭的最終實驗測定模型為

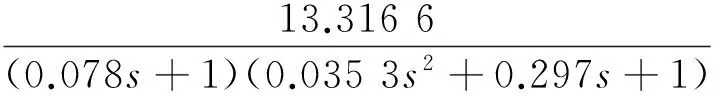
(25)

通過Matlab/Simulink仿真，在t=0時施加一個階躍輸入信號u=0.579 2，所得階躍響應曲線如圖6所示，并與力控法蘭實際響應曲線對比進行模型驗證。

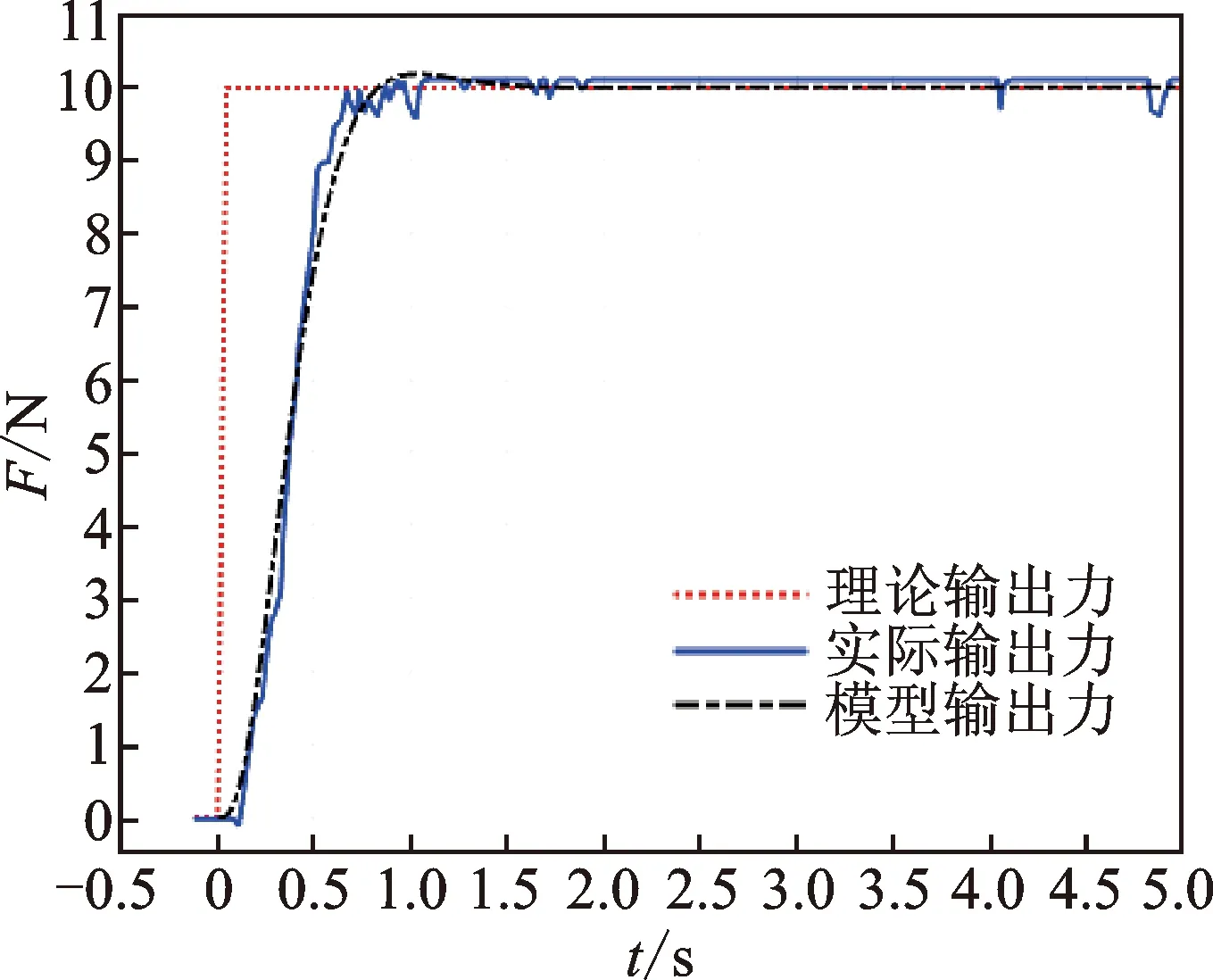
圖6 模型驗證Fig.6 Model verification

從圖6可以看出，模型輸出力響應曲線與實際輸出力響應曲線總體來說比較接近，說明該模型較好地還原實際模型。但由于實驗模型在測定過程中忽略了其高階項，且實際響應曲線的獲取受很多未知因素的影響，數據在一定范圍內具有不確定性，因此其上升曲線與實際響應稍有差異。通過對比式(15)理論模型與式(25)實驗測定模型可知，兩者均為無零點的三階傳遞函數，從而驗證了理論建模的正確性。因此，實驗測定模型可認為是力控法蘭系統的近似數學模型。力控法蘭被施加階躍輸入信號后，輸出力基本無超調，說明系統的穩定性良好。由于三階系統存在多個慣性環節，使得實際輸出響應存在一定的滯后。為了滿足工業應用上對系統快速性的要求，需要在此基礎上對力控法蘭控制系統的快速響應性能進行改善。

3 控制器設計

3.1 控制框架

力控法蘭裝置的控制原理如圖7所示。圖中：F0為期望力(設定值)；u為控制器輸出給伺服閥的控制信號；P為伺服閥輸出到氣缸腔內氣體形成的氣壓；Fn為氣缸腔內氣壓向下產生的壓力，即力控法蘭輸出力；Pb為壓力傳感器檢測反饋的氣缸腔內氣壓；Fb為根據壓力傳感器反饋氣壓值換算所得，經過標定Fb可準確反饋力控法蘭輸出力Fn，理論上控制系統穩定后，該值等于設定值F0，從而實現末端接觸力的恒力控制；Xb為位移傳感器測出的力反饋裝置的柔順變形位移量，可以用來檢測感知力控法蘭的狀態。

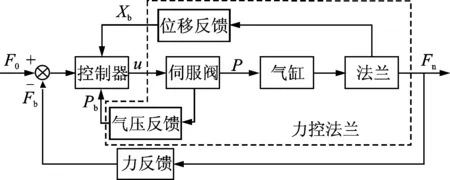
圖7 力控法蘭控制系統原理圖Fig.7 Control system schematic diagram of force-controlled flange

力控法蘭的輸出力控制具體實現過程如下：在裝置啟動前給定目標接觸力F0，控制器根據控制算法得出應該分配給伺服閥的控制信號u，伺服閥根據控制信號u向氣缸輸出相應的氣壓P，并將實際的氣壓值反饋給控制器，從而得到反饋力Fb。Fb與設定值F0比較，根據所得誤差進行下一步的調節，最終使Fb在控制精度范圍內等于F0，從而實現對法蘭輸出力的控制。可以看出，在此過程中，控制器的控制性能直接影響輸出力的動態特性和穩定性。

3.2 控制器設計

傳統的PID控制方法控制簡單且具有良好的穩態精度，然而在系統的抗干擾性及對系統參數時變的魯棒性都不夠理想。力控法蘭在運行的過程中具有許多的非線性因素(如氣缸摩擦力、被動柔順產生的位移變化，以及與工件接觸的等效剛度等)，因此，實驗測定的數學模型只能作為對力控法蘭進行控制的近似模型。模糊控制是基于模糊推理和模仿人的思維的方法，不需要精確的系統數學模型，具有較強的魯棒性，但是單獨控制時會產生一定的穩態誤差。筆者結合PID控制器與模糊控制器的優點，對力控法蘭系統進行控制優化，根據設定的輸入信號和反饋信號，計算誤差e以及當前誤差變化率ec，通過模糊規則進行模糊推理，同時通過PID控制進行調節，將兩個控制器的控制量合并輸出，從而實現力控法蘭的末端輸出信號的控制。控制系統框圖如圖8所示。

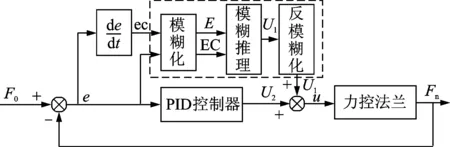
圖8 模糊PID控制框圖Fig.8 Fuzzy PID control block diagram

圖8中，F0為期望力(設定值)，Fn為力控法蘭的輸出。模糊控制器以誤差e和誤差變化率ec作為輸入，控制量u1作為輸出，與PID控制器輸出的控制量u2合并為系統的控制量u，實現對力控法蘭的末端輸出力Fn的控制，使之快速達到設定值并保持穩定。

模糊控制器設計流程如圖9所示。主要有4個步驟：a.對系統輸入輸出進行模糊化處理；b.模糊控制規則提取；c.模糊推理和決策表生成；d.輸出的反模糊化處理。

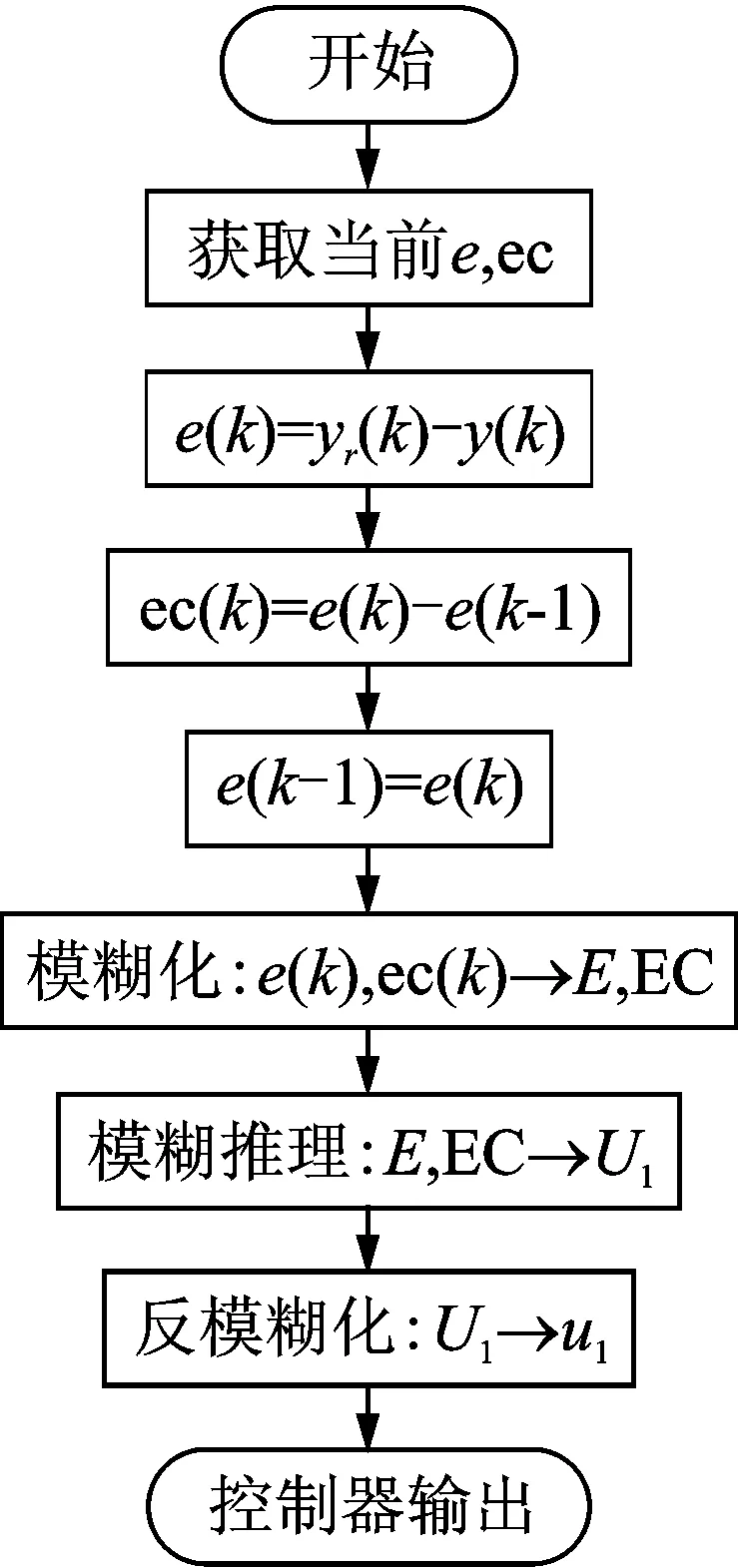
圖9 模糊PID控制器設計流程圖Fig.9 Flow chart of fuzzy PID controller design

對系統的輸入e和ec以及輸出u1均采用7段模糊子集{負大，負中，負小，零，正小，正中，正大}描述，記為{NB,NM,NS,ZO,PS,PM,PB}。論域設定為[-6,6]。考慮到對論域的覆蓋程度和靈敏度，各模糊子集均選用三角形隸屬函數。

控制器設計的原則是通過控制器輸出的控制量使系統快速地達到設定目標值并保持穩定。模糊規則的選取直接影響到系統控制的動態性能和穩態性能。

1) 當e較大，此時無論ec為何值，控制量均應該增加以消除誤差。

2) 當e較小或等于0，此時為了防止超調過大并使系統快速穩定，需要根據ec來確定控制量的變化。如果ec為正，則說明誤差有增大的趨勢，應該加大控制量，以抑制誤差增大；如果ec為負，則說明誤差在減小，此時控制量可取較小值。

根據上述原則，建立模糊控制規則，如表1所示。

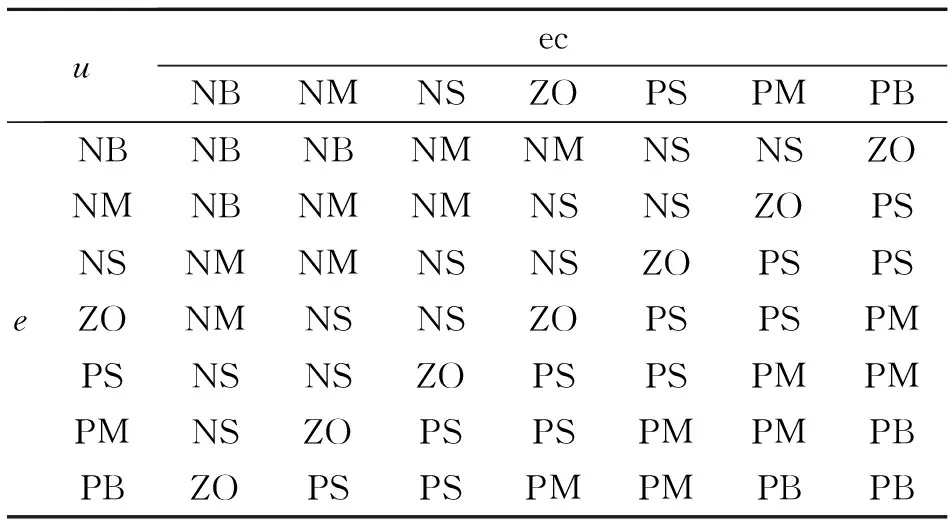
表1 模糊控制規則表Tab.1 Fuzzy control rule table

建立模糊規則后，應用模糊推理得到輸出模糊量U1，再反模糊化得到實際控制量u1。由于模糊控制最終會存在一定的穩態誤差，PID控制器的積分作用可以消除穩態誤差，實現對設定值的無靜差跟蹤。因此，采用經典PID控制器對模糊控制器進行改進，由PID控制器輸出控制量u2，與模糊控制器輸出的控制量u1合并為總控制量u，對力控法蘭進行控制。

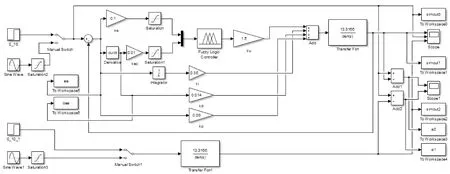
圖10 力控法蘭模糊PID控制Simulink模型Fig.10 Fuzzy PID control simulink model of force-controlled flange

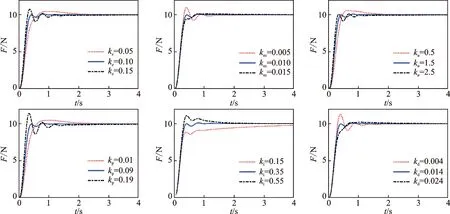
圖11 參數ke,kec,ku,kp,ki,kd對階躍響應的影響Fig.11 Parameters ke,kec,ku,kp,ki,kd effect on step response

4 仿真與實驗驗證

4.1 仿真驗證

為了驗證模糊PID控制器對力控法蘭動態性能的影響，采用Simulink工具進行仿真。搭建仿真模型如圖10所示，模型包括階躍輸入、模糊控制器、PID控制模塊、控制對象及系統輸出。其中模糊控制器為使用Simulink中的模糊控制工具箱建立的Mamdani模糊控制器，PID模塊的比例、積分和微分輸出的控制量直接與模糊控制輸出的控制量合并為力控法蘭模型的控制輸入。

模糊規則確定后，模糊控制部分可調節的參數有ke，kec，ku。其中:ke，kec為輸入誤差和誤差變化率的量化因子；ku為輸出控制信號的量化因子。分別對模糊控制參數及PID控制參數kp，ki，kd進行調節。各參數取值對響應曲線的影響如圖11所示。

從圖11可以看出，ke和kp對系統的調節時間影響明顯。ke，kp越大，響應越迅速，但參數增大，提高響應時間的同時也引起系統的振蕩和超調。kec，kd對系統的超調有抑制作用，但是會使系統穩定的時間變長。ku作為輸出控制量的量化因子，對系統的輸出有很直觀的作用，而積分系數ki對系統趨于穩態值的速度影響顯著。積分環節消除穩態誤差的作用在圖12可進一步明確。

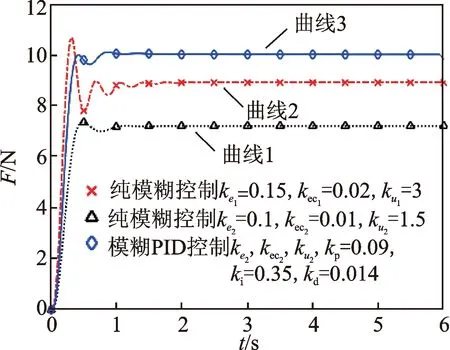
圖12 響應曲線對比Fig.12 Response curve comparison

圖12中，曲線1和曲線2均存在一定的穩態誤差。對比曲線1和曲線2可知，采用單純模糊控制時，量化因子取值不同，系統最終產生的穩態誤差不一樣。在曲線1的基礎上增加PID控制，系統階躍響應如曲線3所示。ki消除了曲線1的穩態誤差，使系統穩定在設定目標值。另外，由于PID參數中的kp作用與ke相似，kd作用與kec相似，因此，得到某一較理想響應曲線的控制參數可能并不唯一。

為了驗證模糊PID控制器的控制效果，分別在對模型進行階躍響應仿真和正弦跟隨仿真。在t=0時輸入信號F0=10 N，得到仿真階躍響應曲線如圖13(a)所示。從仿真結果可以看出，未加模糊PID控制的實驗測定模型的階躍響應時間為0.69 s，并存在1.7%的超調量，加模糊PID控制后，系統仿真的階躍響應時間縮短為0.34 s，經過兩次很小的振蕩后系統進入穩定狀態，基本不存在超調，系統的動態性能和穩態精度都得到了提高。采用頻率為0.5 Hz、幅值為10 N的正弦信號作為給定輸入信號。系統跟隨響應曲線如圖13(b)所示。可以看出，加模糊PID控制器后，系統的動態調節速度明顯提高，系統響應的滯后明顯改善；但由于頻率變化太快，系統的幅值削弱較明顯。

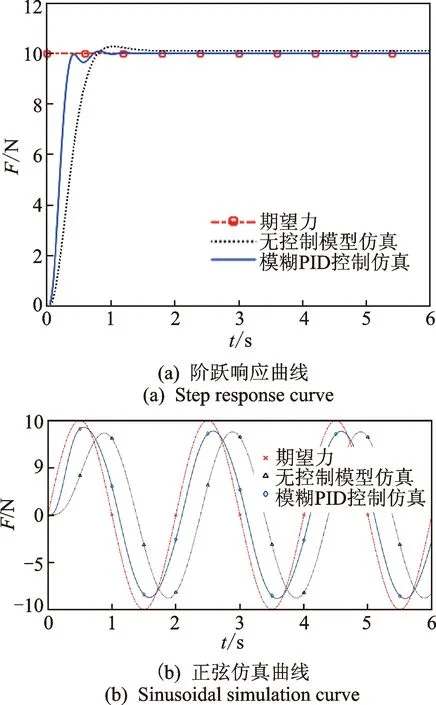
圖13 加模糊PID控制前后仿真對比Fig.13 Simulation comparison before and after fuzzy PID control

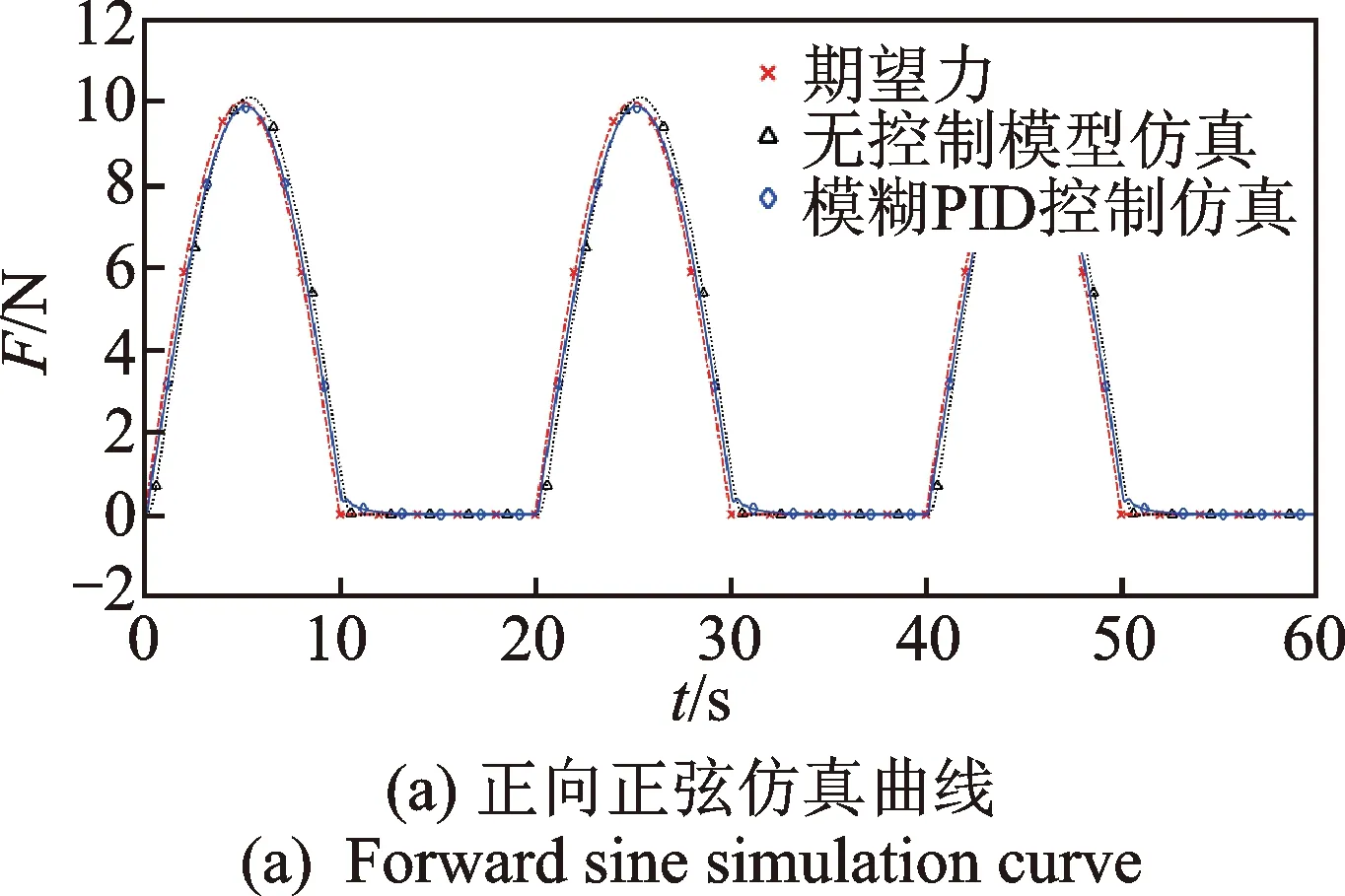
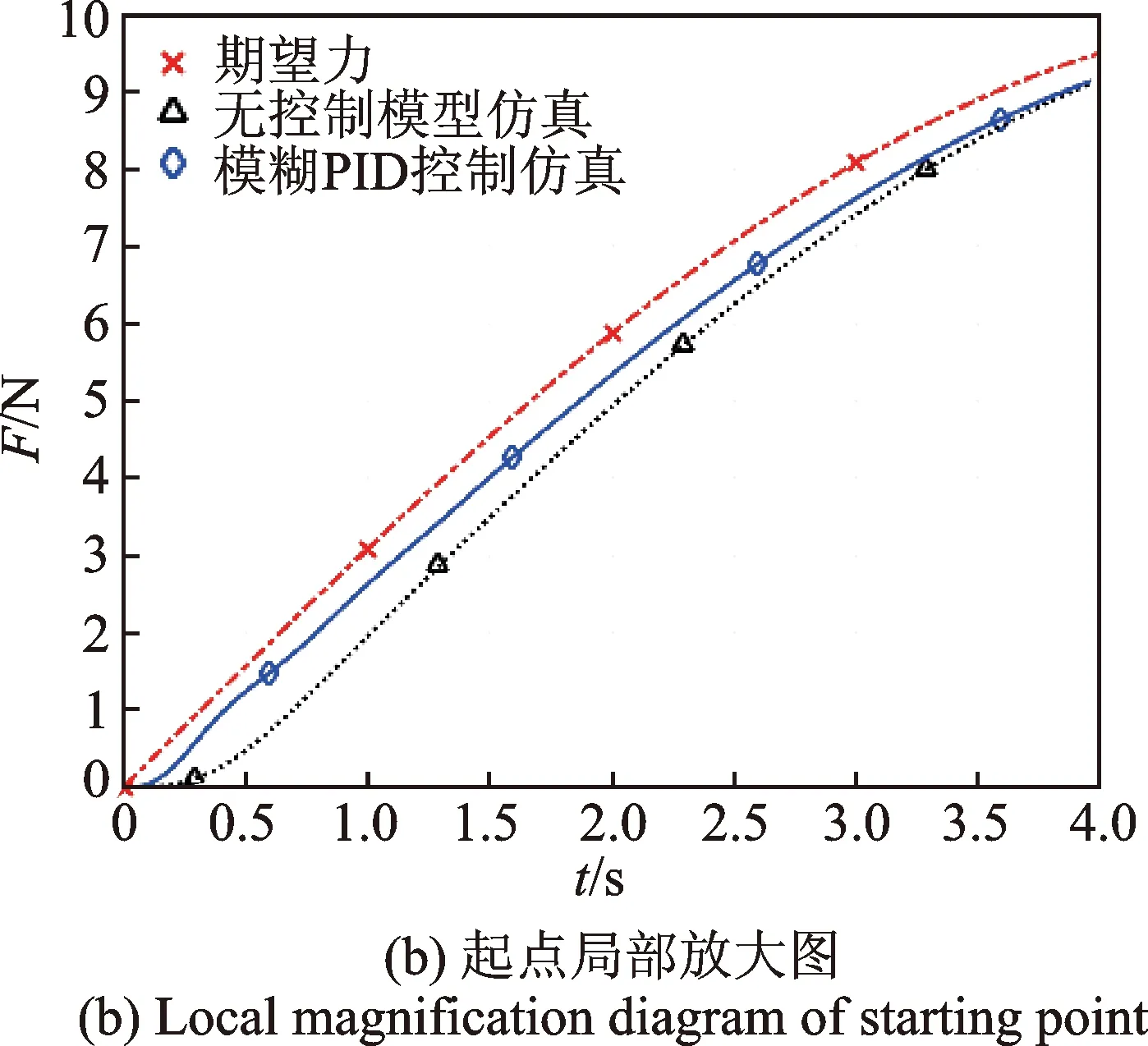
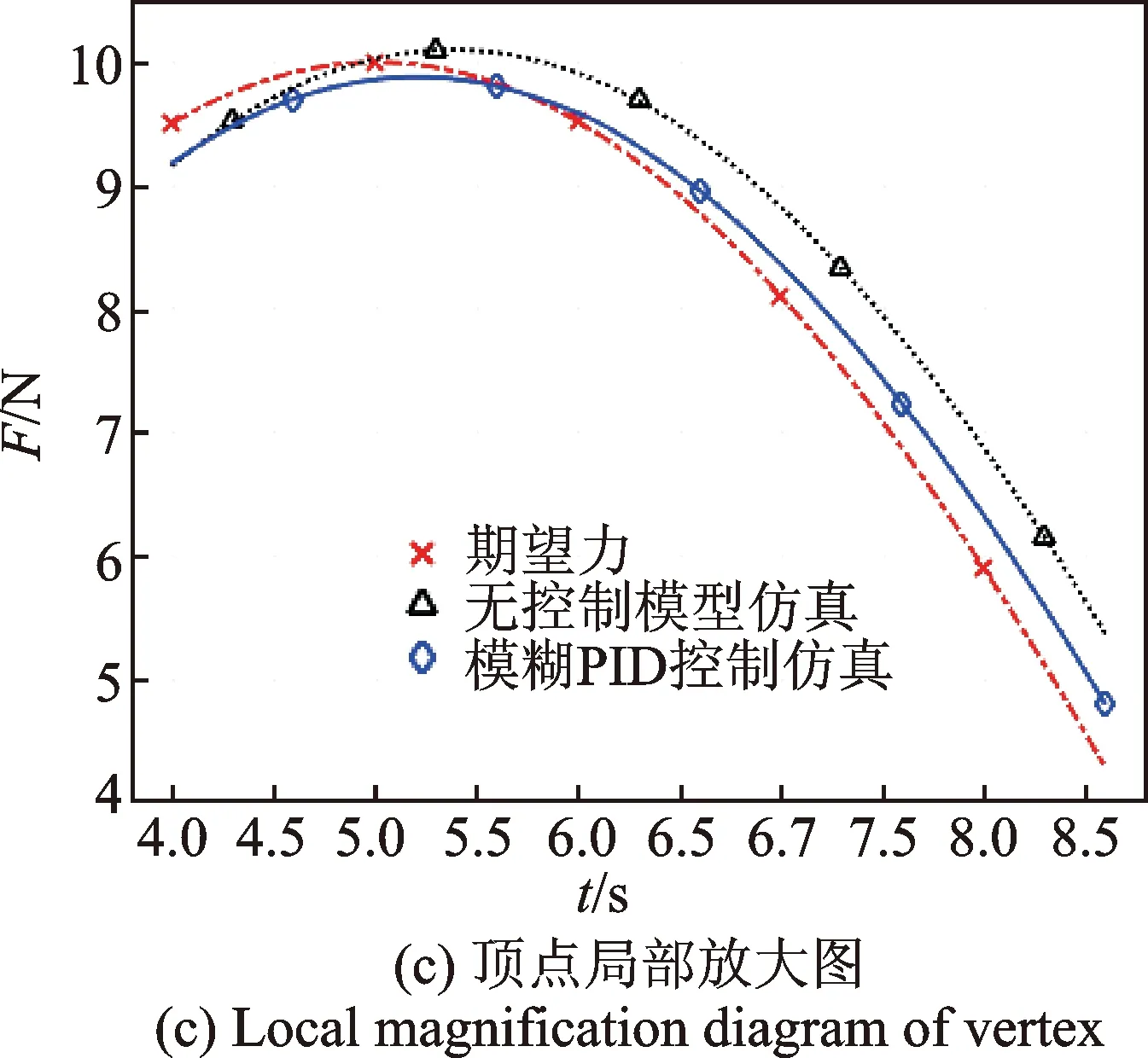
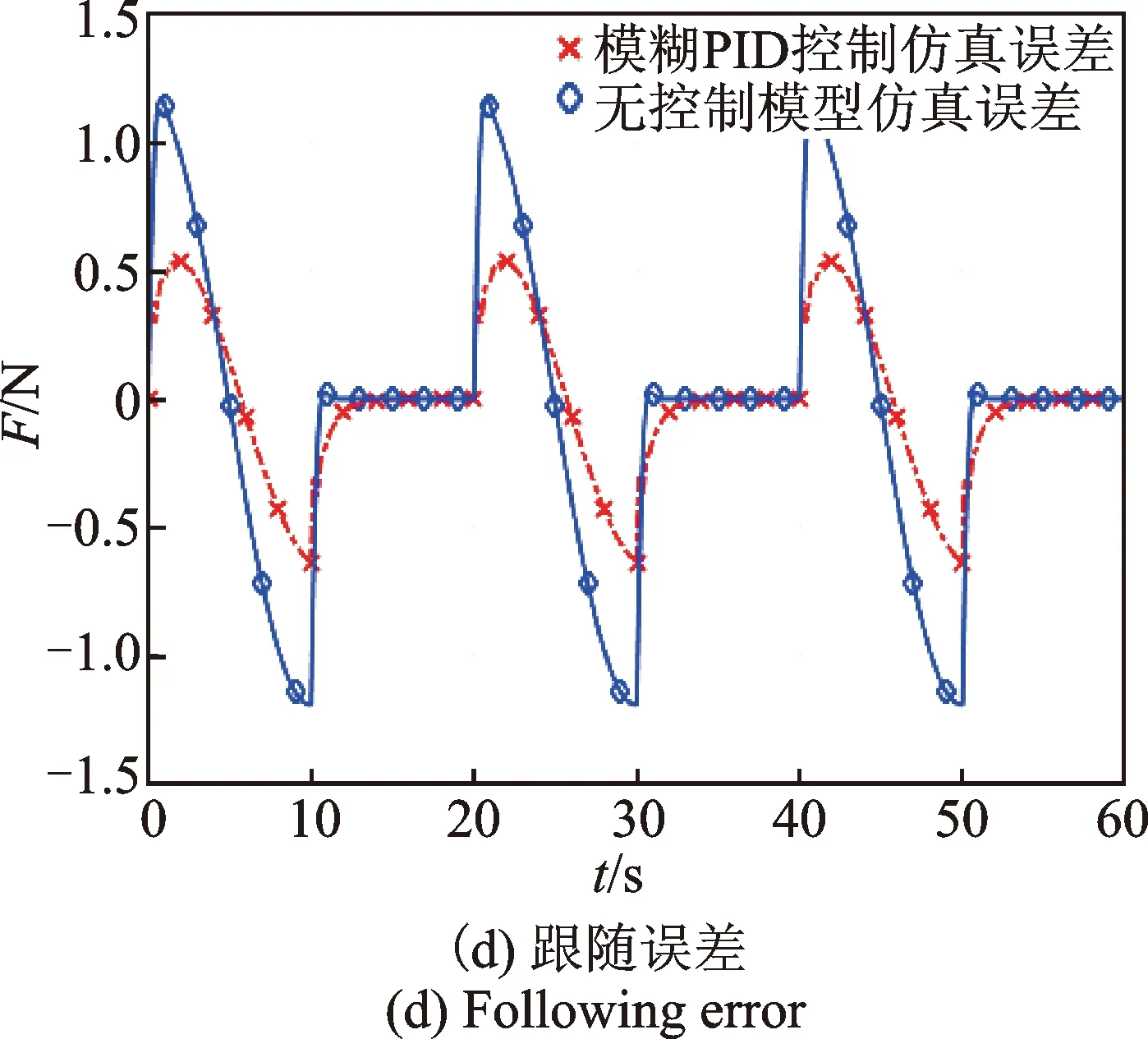
圖14 正向正弦跟隨仿真Fig.14 Forward sine following simulation

降低給定信號頻率，采用頻率為0.05Hz、幅值為10 N的正弦信號作為給定輸入信號。考慮力控法蘭控制信號不小于0，將正弦輸入信號的負值部分過濾后進行仿真，獲得仿真結果如圖14所示。圖14(a)為前3個周期的響應曲線，從整體來看系統跟隨性良好。圖14(b)～(c)分別為響應曲線起點和頂點的局部放大圖。可以看出，加模糊PID控制后，在起點處稍有振蕩然后迅速進入跟隨狀態，且其響應曲線延遲明顯小于無模糊PID控制的響應曲線。從圖14(d)可知，加模糊PID控制之后，力控法蘭仿真的輸出力跟隨誤差由±1.2 N減小為±0.6 N。綜合以上，加模糊PID控制器后，系統的動態調節性能及跟隨魯棒性明顯改善。

4.2 實驗驗證

為了進一步驗證模糊PID控制器對力控法蘭裝置動態性能的影響以及其跟隨魯棒性，搭建基于Labview的力控法蘭半實物實驗平臺，如圖15所示。平臺主要由力控法蘭裝置、PCI1710u數據采集卡及其接口板和計算機組成。實驗中，為了盡量減少其他非線性因素對實驗的影響，使力控法蘭裝置保持垂直向下的狀態，不連接加工工具，可以不考慮法蘭在加工運行中由位姿變化引起的受力變化和固定在法蘭末端的工具重力。需要進行兩組實驗：a.階躍響應實驗,在實驗中設定目標力F=10 N，給定氣泵壓力為0.7MPa，分別記錄加模糊PID控制前后力控法蘭輸出力反饋值;b.正弦響應實驗,選擇幅值為10、頻率為0.05Hz的正弦波信號，截取其正向部分作為控制器的給定信號，數據采集卡采集周期為10 ms，分別記錄加模糊PID控制前后力控法蘭輸出力的反饋值。

圖15 力控法蘭實驗平臺Fig.15 Force-controlled flange experimental platform

階躍響應實驗響應曲線結果如圖16所示。設定力控制信號F=10 N，兩種情況下獲得的末端輸出力的響應曲線如圖16所示。雖然采集的數據受噪聲干擾存在一定的波動，但仍可以看出，增加模糊PID控制器后，力控法蘭響應時間明顯減小，其動態調節性能顯著提升。

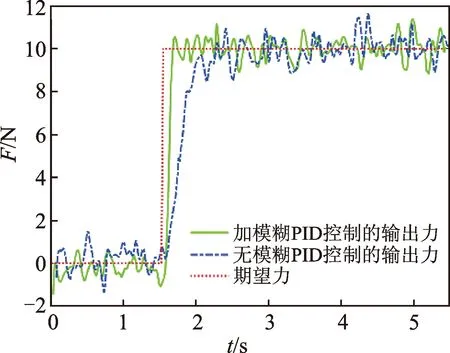
圖16 加模糊PID控制前后階躍響應實驗曲線對比Fig.16 Comparison of experimental curves of step response before and after fuzzy PID control

正弦跟隨實驗結果如圖17所示。圖17(a)顯示無模糊PID控制時，響應曲線延遲明顯，加模糊PID控制器后，響應曲線延遲減小，與給定信號基本重合。響應曲線跟蹤誤差如圖17(b)所示，跟蹤誤差由大約±3 N減小為大約±1.5 N。可見，實驗結果與仿真結果相符。增加模糊PID控制器后，力控法蘭的動態響應性能及跟隨控制性能得到了提高，系統具有較強的魯棒性。

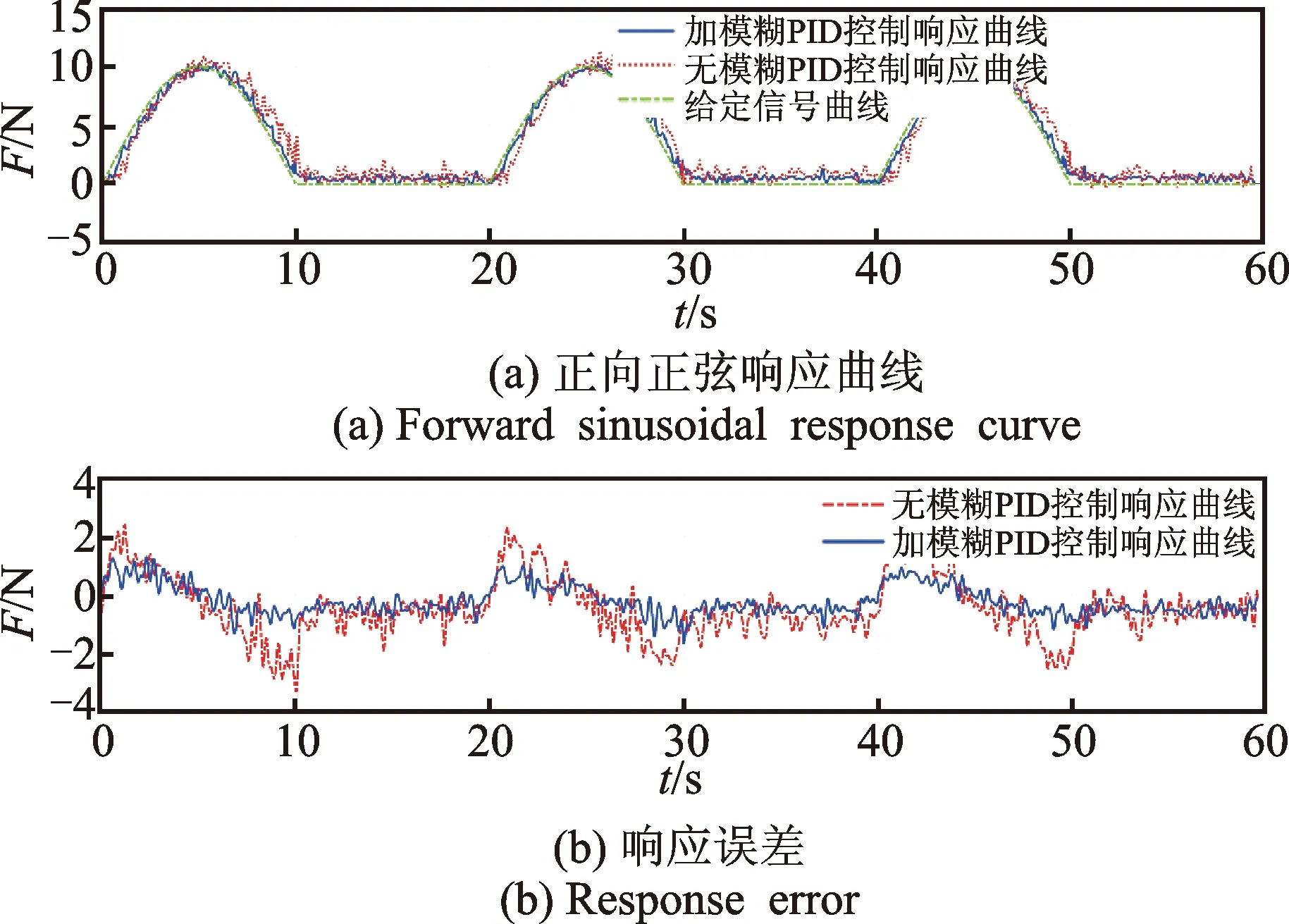
圖17 正向正弦響應實驗結果Fig.17 Experimental results of forward sinusoidal response

為了更直觀地驗證力控法蘭的末端輸出力控制的穩態魯棒性，將力控法蘭裝置安裝于機器人末端，另一端安裝打磨工具。在鋁合金工件上實際運行一條加工軌跡。設定法蘭接觸力為F=10 N，運行過程中保持工具與工件的法向接觸，工具的重力根據運行的姿態進行重力補償。得到末端輸出力反饋數據如圖18所示。最終實際接觸力在期望力的±0.8 N范圍內波動，輸出力控制穩定性較好。

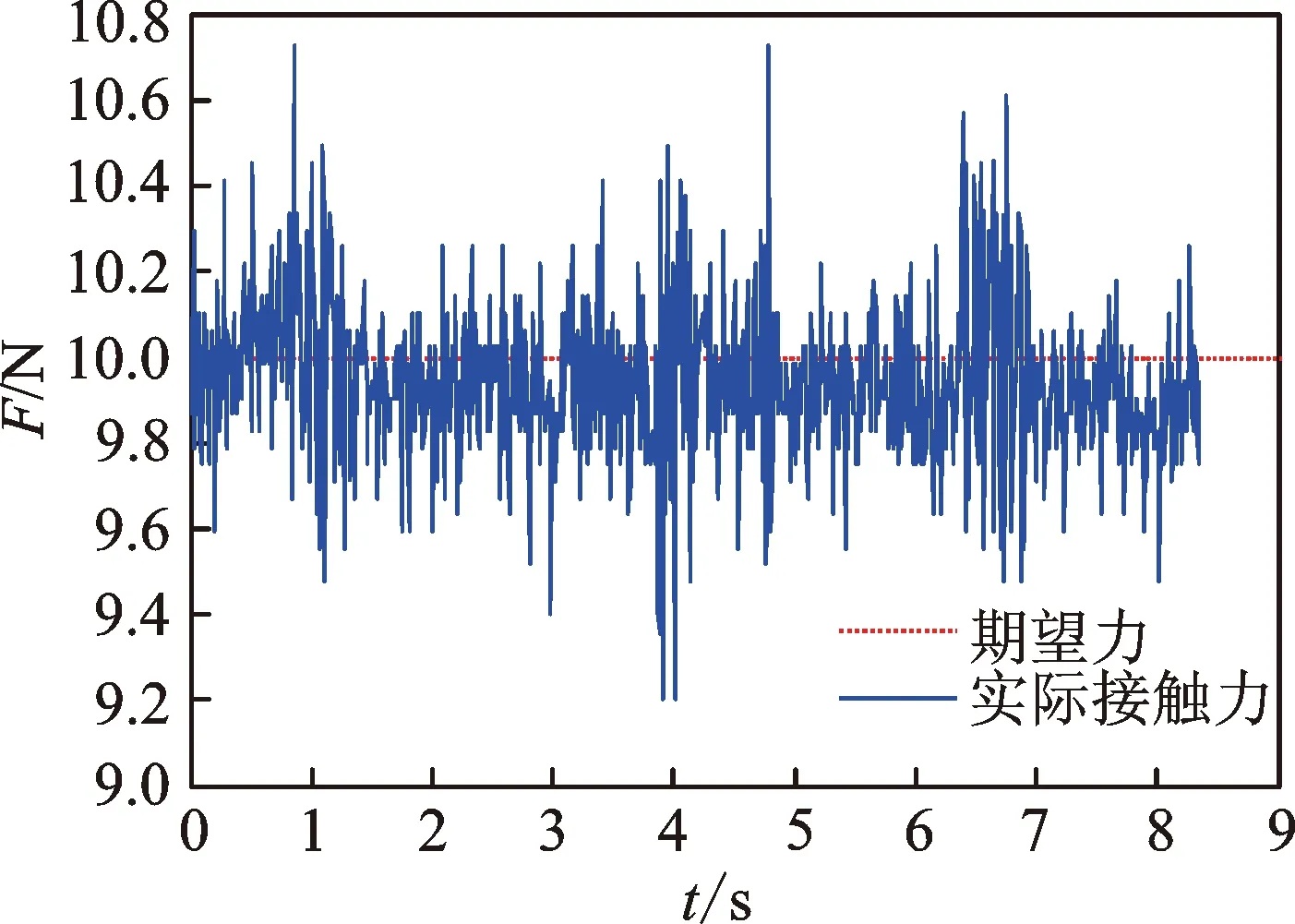
圖18 力控法蘭輸出力測試Fig.18 Output force test of force-controlled flange

5 結束語

針對機器人進行接觸式作業的過程中對工具末端與工件的接觸力的要求，提出了一種基于模糊PID控制的力控法蘭恒力控制方法。通過理論分析對該裝置進行了建模，并通過實驗測定法獲得了該裝置的近似模型。設計了一種模糊控制與PID控制并行的模糊PID控制器，對系統的動態調節性能進行了優化。仿真結果表明，模糊PID控制器可提高系統的響應時間，并對末端輸出力進行有效跟蹤。搭建基于Labview的半實物仿真平臺，對力控法蘭進行控制實驗。實驗進一步證明了仿真結果，動態響應時間縮短，動態性能明顯優化。正弦跟蹤實驗最大跟蹤誤差小于1.5 N，證明控制器控制穩定性良好,具有較強的魯棒性。最后，通過接觸加工實驗對輸出力進行檢測，驗證了系統具有對末端力的恒力控制能力。

[1] 王田苗,陶永.我國工業機器人技術現狀與產業化發展戰略[J].機械工程學報,2014,50(9):1-13.

Wang Tianmiao,Tao Yong.Research status and industrialization development strategy of Chinese industrial robot[J].Journal of Mechanical Engineering,2014,50(9):1-13.(in Chinese)

[2] Valente A.Reconfigurable industrial robots:a stochastic programming approach for designing and assembling robotic arms[J].Robotics and Computer-Integrated Manufacturing,2016,41:115-126.

[3] Chen Yonghua,Dong Fenghua.Robot machining:recent development and future research issues[J].International Journal of Advanced Manufacturing Technology,2013,66(9-12):1489-1497.

[4] 吳石,劉獻禮,宋盛罡,等.銑刀磨損對銑削穩定性及表面位置誤差的影響[J].振動、測試與診斷,2015,35(4):763-769.

Wu Shi,Liu Xianli,Song Shenggang,et al.The influence of wear loss of milling cutter on milling stability and surface location error[J].Journal of Vibration,Measurement &Diagnosis,2015,35(4):763-769.(in Chinese)

[5] Siciliano B,Sciavicco L,Villani L,et al.Robotics:modelling,planning and control[M].[S.l.]:Springer Publishing Company,Incorporated,2010:363-371.

[6] 孔民秀,游瑋,杜志江,等.基于速度閉環的自適應力位控制算法[J].哈爾濱工業大學學報,2010,42(3):409-413.

Kong Minxiu,You Wei,Du Zhijiang,et al.Adaptive force/position control algorithm with closed loop of velocity for the haptic device[J].Journal of Harbin Institute of Technology,2010,42(3):409-413.(in Chinese)

[7] Chaudhary H,Panwar V,Prasad R,et al.Adaptive neuro fuzzy based hybrid force/position control for an industrial robot manipulator[J].Journal of Intelligent Manufacturing,2016,27:1-10.

[8] Sakaino S,Sato T,Ohnishi K.Force-based disturbance observer for dynamic force control and a position/force hybrid controller[J].Ieej Transactions on Electrical &Electronic Engineering,2013,8(5):505-514.

[9] Hogan N.Impedance control-an approach to manipulation.I-theory.II-implementation.III-applications[J].Journal of Dynamic Systems Measurement &Control,1985,107(1):1-24.

[10]Huang Han,Gong Zhiming,Chen Xiaoqi,et al.Robotic grinding and polishing for turbine-vane overhaul[J].Journal of Materials Processing Technology,2002(127):140-145.

[11]Jin Mingsheng,Ji Shiming,Pan Ye,et al.Effect of downward depth and inflation pressure on contact force of gasbag polishing[J].Precision Engineering,2017,47:81-89.

10.16450/j.cnki.issn.1004-6801.2017.04.002

* 國家科技支撐計劃資助項目(2015BAF10B00)

2017-06-10;

2017-06-30

TP273.4

黃婷，女，1984年10月生，博士、工程師。主要研究方向為工業機器人控制與應用。曾發表《小功率隨動系統的建模與校正網絡設計》(《南昌航空大學學報：自然科學版》2008年第22卷第1期)等論文。 E-mail：hting104@163.com