單裂紋巖石的力學(xué)行為

吳 峰 鄭 濤 劉友強(qiáng)

(重慶城建控股(集團(tuán))有限責(zé)任公司,重慶 400010)

單裂紋巖石的力學(xué)行為

吳 峰 鄭 濤 劉友強(qiáng)

(重慶城建控股(集團(tuán))有限責(zé)任公司,重慶 400010)

通過(guò)壓縮實(shí)驗(yàn)，利用伺服單軸加載系統(tǒng)對(duì)含單裂紋巖石在壓縮荷載下的破壞準(zhǔn)則進(jìn)行了研究，并利用ABAQUS模擬了單軸壓縮荷載作用下的力學(xué)情況，計(jì)算了復(fù)合裂紋的應(yīng)力強(qiáng)度因子。實(shí)驗(yàn)和數(shù)值結(jié)果表明當(dāng)裂紋傾斜角為45°時(shí)KⅠ和KⅡ基本相等，當(dāng)裂紋方向與荷載方向平行時(shí)，尖端應(yīng)力的強(qiáng)度因子變化曲線(xiàn)將趨近于零。

應(yīng)力強(qiáng)度因子，單裂紋，壓縮荷載，強(qiáng)度，數(shù)值模擬

0 引言

目前，巖體工程界飛速的發(fā)展，節(jié)理巖體的強(qiáng)度、變形及裂隙的擴(kuò)展等特性數(shù)據(jù)是工程設(shè)計(jì)、施工的基礎(chǔ)參考指標(biāo)。

根據(jù)節(jié)理是否連通，巖體可分為含貫通節(jié)理和含斷續(xù)節(jié)理，又根據(jù)節(jié)理內(nèi)空隙的大小、起伏度及其充填物的性質(zhì)和數(shù)量，節(jié)理可以分為張開(kāi)與閉合。很大程度上，巖體的失穩(wěn)破壞是由于巖體節(jié)理裂隙擴(kuò)展、貫通引起的。文獻(xiàn)[1]～[3]用石膏研究了單軸加載下的裂紋和雙裂紋的失穩(wěn)模式，但是沒(méi)有研究?jī)A角和裂紋的擴(kuò)展路徑等問(wèn)題，文獻(xiàn)[4]～[8]從理論上研究了單雙軸作用下裂紋的貫通機(jī)制，但是沒(méi)有給予充分的驗(yàn)證。在壓縮荷載作用下，裂紋擴(kuò)展，分叉并相互連通。

1 實(shí)驗(yàn)研究

1.1 試件制作

實(shí)驗(yàn)試件為河砂、石膏粉、水泥按照一定比例配制而成。此試件具有與天然巖石相似的重要特性：脆性特性和剪脹特性(單軸壓縮)。實(shí)驗(yàn)試件主要選擇425普通水泥、最大粒徑2 mm的天然砂為原料，配比調(diào)試而成。

實(shí)驗(yàn)采用預(yù)埋鋼片的方式瑣制貫通型裂紋，鋼片寬10 mm，厚1 mm，實(shí)驗(yàn)所用正方形薄板尺寸為200 mm×200 mm。

1.2 加載裝置

加載裝置采用萬(wàn)能試驗(yàn)機(jī)，實(shí)驗(yàn)時(shí)在試件端部放置墊鐵以減少摩擦力。

2 實(shí)驗(yàn)結(jié)果分析

2.1 裂紋傾角對(duì)混凝土壓縮強(qiáng)度的影響

為了研究裂紋傾角對(duì)混凝土壓縮強(qiáng)度的影響，固定其他參數(shù)，而裂紋的傾角分別選擇0°～90°，以15°為梯度均勻變化，其他參數(shù)保持不變。圖1給出了實(shí)驗(yàn)測(cè)試結(jié)果。

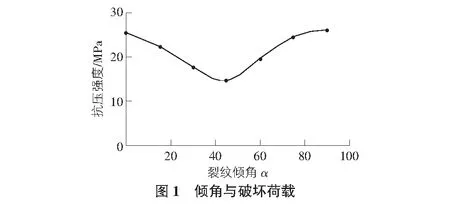
從圖1可以看出，試件抗壓強(qiáng)度和裂隙傾角有很大關(guān)系。當(dāng)裂紋傾角為45°時(shí)，試件破壞最快，強(qiáng)度最低，較大或較小的慣角，對(duì)壓縮強(qiáng)度的影響不明顯。

2.2 荷載位移曲線(xiàn)

圖2給出了傾角為45°時(shí)的荷載位移曲線(xiàn)，從圖上可以看出，裂紋的發(fā)展大致經(jīng)歷以下幾個(gè)階段。

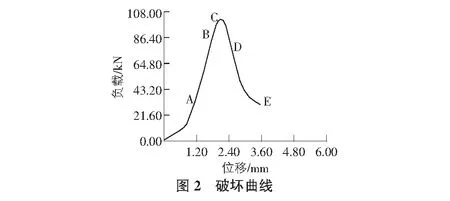
2.3 裂紋擴(kuò)展

為了研究壓縮荷載作用下，裂紋的擴(kuò)展情況，選取了角度為30°，45°,60°,75°的試件，圖3是荷載作用下的翼型裂紋擴(kuò)展情況。

實(shí)驗(yàn)結(jié)果表明：翼型從原裂紋端部開(kāi)始產(chǎn)生，初始較短，并不明顯，但是隨著載荷的增大，裂紋長(zhǎng)度增長(zhǎng)迅速，并逐漸擴(kuò)展至試件頂端。此時(shí)，載荷下降，次生裂紋從原裂紋的端部逐步產(chǎn)生，最終試件破碎。

3 基于ABAQUS的數(shù)值模擬技術(shù)

3.1 利用ABAQUS計(jì)算KⅠ與KⅡ

斷裂力學(xué)的研究表明：

(1)

在Ⅰ型和Ⅱ型復(fù)合裂紋情況下，求解出來(lái)的J積分是KⅠ和KⅡ的函數(shù)，可以通過(guò)J積分求解出Ⅰ型和Ⅱ型裂紋的應(yīng)力強(qiáng)度因子KⅠ和KⅡ。但是只求解出一個(gè)J積分是無(wú)法得到兩個(gè)應(yīng)力強(qiáng)度因子的，Ishikawa[3]將Ⅰ型和Ⅱ型復(fù)合型裂紋的J積分進(jìn)行了如下分解：

(2)

復(fù)合型裂紋J積分的分解圖如圖4所示。

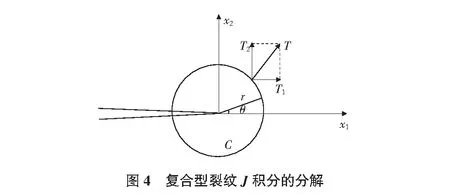
在計(jì)算出JⅠ和JⅡ后，就可以求解出Ⅰ型和Ⅱ型復(fù)合裂紋的應(yīng)力強(qiáng)度因子KⅠ和KⅡ。

采用ABAQUS軟件計(jì)算裂紋尖端的應(yīng)力強(qiáng)度因子。在有限元中計(jì)算二維的線(xiàn)積分是不容易且不準(zhǔn)確的，但是計(jì)算二維的面積積分卻不存在上面的困難。因此在有限元中通常利用Stokes公式將J積分中的線(xiàn)積分轉(zhuǎn)化成為面積分計(jì)算。

基于ABAQUS斷裂力學(xué)，定義了沿任意擴(kuò)展方向下的J積分：

(3)

式(3)中的vs即為裂紋擴(kuò)展方向的單位向量；ω為工程應(yīng)變能密度；ns為積分曲線(xiàn)的外法線(xiàn)，方向背向裂紋尖端。該定義是前面J積分定義的推廣，它可以適用于任意的裂紋擴(kuò)展方向。下面簡(jiǎn)介在ABAQUS中通過(guò)圍線(xiàn)積分計(jì)算J積分的基本關(guān)系式。

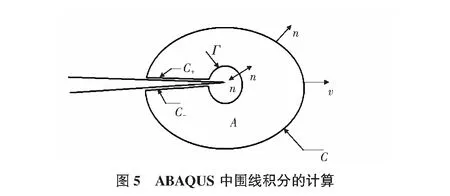
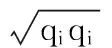
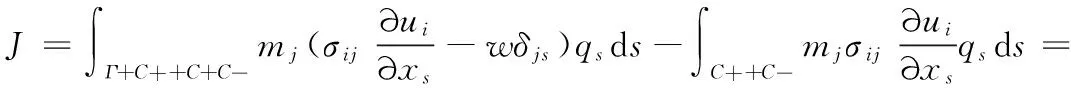
(4)

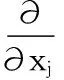
在ABAQUS中采用等價(jià)彈性材料的概念，認(rèn)為工程應(yīng)變能密度是工程應(yīng)變的函數(shù)：

所以：

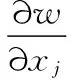
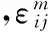
進(jìn)一步化簡(jiǎn)I的表達(dá)式：

代入到公式中，得到J積分的表達(dá)式：

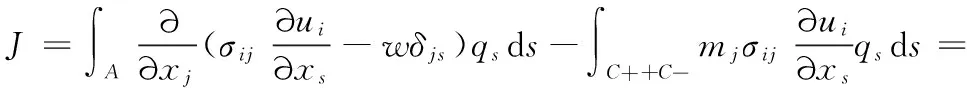
(5)

ABAQUS在計(jì)算圍線(xiàn)積分時(shí)，采用的是先計(jì)算出圍線(xiàn)上面所取的若干個(gè)離散點(diǎn)處J積分值，然后乘以每個(gè)點(diǎn)對(duì)應(yīng)的加權(quán)值后，所有點(diǎn)相加來(lái)近似地求解出圍線(xiàn)積分，即J積分的值JⅠ和JⅡ，進(jìn)而得到復(fù)合裂紋的應(yīng)力強(qiáng)度因子KⅠ和KⅡ。

3.2 利用ABAQUS比較應(yīng)力強(qiáng)度因子隨裂紋角度的變化規(guī)律

依據(jù)試件尺寸，建立模型。尺寸為150 mm×150 mm，裂紋長(zhǎng)度10 mm；定義材料參數(shù)，彈性模量E=20 GPa,泊松比v=0.3；壓縮荷載20 MPa。

應(yīng)力強(qiáng)度因子和傾角的關(guān)系如圖6所示。

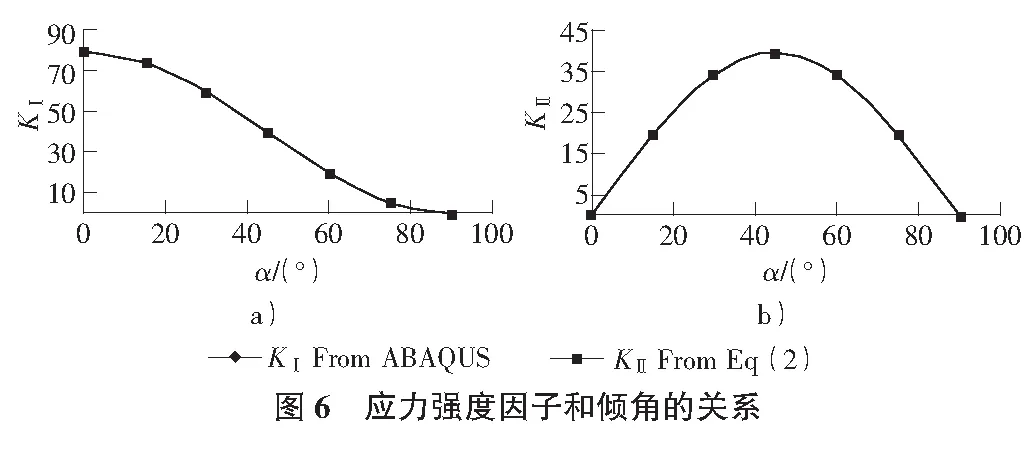
從數(shù)值模擬結(jié)果來(lái)看，應(yīng)力強(qiáng)度因子KⅠ隨著傾角的增大而減小，而KⅡ則以45°為極大值點(diǎn)，變化趨勢(shì)先增大，后減小。這與實(shí)驗(yàn)結(jié)果很好的符合。

4 結(jié)語(yǔ)

巖石類(lèi)脆性材料的破壞，單就力學(xué)效應(yīng)來(lái)講，當(dāng)材料的受力超過(guò)其承載能力極限時(shí)，材料即失穩(wěn)破壞。微觀裂紋的擴(kuò)展和相互連通使得損傷加強(qiáng)，且進(jìn)一步增加損傷的局部化，直到形成宏觀裂紋，最后導(dǎo)致破壞。

裂尖應(yīng)力強(qiáng)度因子是度量裂尖應(yīng)力場(chǎng)和位移場(chǎng)大小的量，從文中可以看出受到一些參數(shù)的影響，包括裂紋本身的長(zhǎng)度、傾斜角以及其他裂紋對(duì)其的影響(包括其他裂紋的長(zhǎng)度和邊裂紋間的距離)。在傾斜角為45°時(shí)KⅠ和KⅡ基本相等，平行于載荷方向的裂紋，尖端應(yīng)力強(qiáng)度因子將趨近于零。

[1] Reys O，Einstein H H.Fracture mechanism of fractured rock-fracture coalescence mode[C].Balkema A A.Proc 7th Int Conf on Rock Mech.Germany,1991:333-340.

[2] Shen B,Stephansson O,Einstein H H,et al.Coalescence of fractures under shear stress experiments[J].Jonrnal of Geophysical Research,1995,100(B4):5975-5990.

[3] Bobet A,Einstein H H.Fracture coalescence in rock-type material under uniaxial and biaxial compression[J].Int J Rock Mech Min Sci,1998,35(7):836-888.

[4] Horii H,Nemat-Nasser S.Brittle fracture in compression splitting and vbrittle-ductile transition[J].Philosophical Transitions of the Royal Society of London:Series A,1986,319(1549):337-374.

[5] 范天佑.斷裂理論基礎(chǔ)[M].北京：科學(xué)出版社，2003.

[6] 鄧華鋒，胡亞運(yùn)，李建林，等.考慮滯后效應(yīng)的巖石加卸載響應(yīng)比試驗(yàn)研究[J].巖石力學(xué)與工程學(xué)報(bào)，2015,34(sup)：2915-2921.

[7] 趙 程，劉豐銘，楊 磊，等.巖石單裂紋擴(kuò)展及損傷演化規(guī)律的數(shù)值模擬研究[J].重慶交通大學(xué)學(xué)報(bào)(自然科學(xué)版),2016,35(5):22-27.

[8] 趙 程,田加深,松田浩,等.單軸壓縮下基于全局應(yīng)變場(chǎng)分析的巖石裂紋擴(kuò)展及其損傷演化特性研究[J].巖石力學(xué)與工程學(xué)報(bào),2015,34(4):763-769.

[9] 蔣明鏡,陳 賀,劉 芳.巖石微觀膠結(jié)模型及離散元數(shù)值仿真方法初探[J].巖石力學(xué)與工程學(xué)報(bào),2013,32(1):16-23.

[10] 謝其泰，郭俊志，王建力，等.單軸壓縮下含傾斜單裂紋砂巖試件裂紋擴(kuò)展量測(cè)研究[J].巖土力學(xué)，2011,32(10):2917-2921.

The mechanics behavior of single crack rock

Wu Feng Zheng Tao Liu Youqiang

(ChongqingUrbanConstructionHolding(Group)Co.,Ltd,Chongqing400010,China)

The failure property of single cracked samples under compressive load was focused in this experimental study. It is based on the finite element idea, in this paper, single crack in an infinite plate under compression have been investigated by ABAQUS, calculation of mixed-mode crack stress intensity factor. The experimental and numerical results shows that when the crack inclination is 45°KⅡis equal withKⅠ. When the crack at the same direction with the loads, the value of stress intensity factor approaches zero.

stress intensity factor, a single crack, compressive load, strength, numerical simulation

1009-6825(2017)22-0053-03

2017-05-24

吳 峰(1982- )，男，碩士，工程師，一級(jí)建造師； 鄭 濤(1988- )，男，工程師； 劉友強(qiáng)(1976- )，男，工程師，一級(jí)建造師

TU457

A