基于復合置亂算法的數字圖像加密系統設計與實現

孔軍輝+趙冬梅+宋陽

摘 要：分析了目前比較流行的Arnold 算法和騎士巡游算法各自的特點，利用兩種算法之間的互補性，設計了基于Arnold變換和騎士巡游變換相結合的復合置亂算法，并對數字圖像進行加密。該設計以Altera公司的NIOSⅡ嵌入式軟核處理器為核心，創建了用戶自己的數字圖像處理芯片。

關鍵詞：Arnold 算法；騎士巡游算法；復合置亂；圖像加密

DOIDOI：10.11907/rjdk.171332

中圖分類號：TP309.7

文獻標識碼：A 文章編號文章編號：1672-7800（2017）008-0179-03

0 引言

隨著網絡和多媒體技術的發展及應用，以數字圖像信號為主要載體的數據應用已逐漸成為人們生活的主旋律。它雖然給人們生活帶來了便利，但同時也存在著安全隱患。據統計，全世界幾乎每20s就會發生黑客入侵事件。不法者經常會在數字圖像信號傳輸或存儲過程中竊取信息。因此，保護這些圖像信息的安全尤為重要。目前，對數字圖像進行加密處理是解決這類問題的主要手段之一[1]。

1 加密算法選擇

對數字圖像進行隱藏和偽裝有很多種算法，主要有數字圖像置亂技術、數字圖像信息隱藏技術、數字圖像水印技術和數字圖像分存技術[2]。本文采用的是數字圖像置亂技術，這種技術主要利用數字圖像的矩陣性，對圖像中像素的位置或顏色進行擾亂，從而解決數字圖像的安全問題。目前，比較流行的置亂技術有Arnold置亂算法和騎士巡游置亂算法。

1.1 Arnold置亂算法

Arnold 變換是在遍歷理論研究中提出的一種變換，俗稱貓臉變換[3]，具體變換公式如式（1）。 定義：設有單位正方形上的點（ x，y ），將點（ x，y） 變到另一點（ x′，y′）的變換為：

x′y′=1 11 2xy（mod1）

（1）

由式（1）可知，Arnold 變換實際上就是將數字圖像中代表像素的顏色值或灰度值的坐標點進行位置移動的過程，雖然一次移動不能解決問題，但一直重復下去，每一次的最后輸出作為下一次的輸入，經過N次迭代后，就會出現無法辨認的圖像。值得注意的是，隨著迭代次數的增加，迭代到一定數值后數字圖像就會被還原，這說明Arnold變換具有一定的周期性，合理利用此特點，可以幫助人們完成數字圖像的解密工作。

1.2 騎士巡游算法

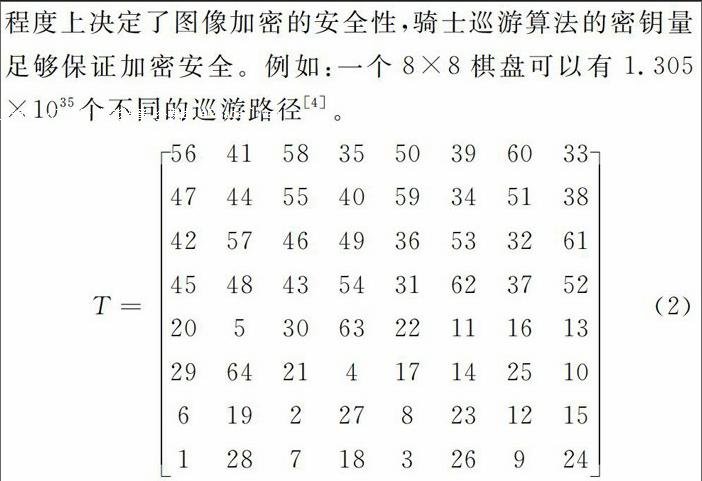
騎士巡游算法，就是讓一個騎士從數字圖像上任意一點像素出發，按照國際象棋“日”字的規則走動，走動過程中要求騎士不重復地走遍n×m棋盤上的每個小方格。騎士巡游路徑不是唯一的，可以用矩陣來表示，此矩陣稱為巡游矩陣。例如在一個8×8的棋盤中，一個騎士從起點1出發，按照式（2）所示矩陣規則進行巡游，直到走完矩陣中的每一點。可以看出，這種算法的密鑰就是巡游矩陣，路徑的數量就是加密的密鑰量。密鑰量的數量在一定程度上決定了圖像加密的安全性，騎士巡游算法的密鑰量足夠保證加密安全。例如：一個8×8棋盤可以有1.305×1035個不同的巡游路徑[4]。

1.3 復合置亂算法

綜上可知，Arnold變換和騎士巡游變換在對數字圖像進行加密處理上有著各自的特點。Arnold變換處理速度快，短時間內置亂效果好，但密鑰量小、安全性不高。騎士巡游算法密鑰量大、安全性高，但速度慢，適合對細節的處理。由于兩種算法之間具有很強的互補性，因此本次設計選擇基于Arnold變換和騎士巡游變換相結合的復合置亂算法，這樣可以做到揚長避短，對數字圖像有著更好的加密效果。

2 系統硬件設計

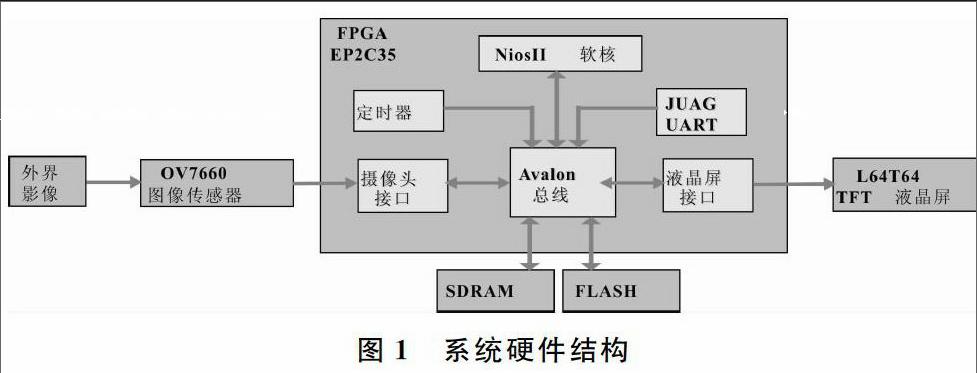
本文采用嵌入式系統SOPC作為圖像加密的硬件平臺，以美國Altera公司Nios II軟核處理器為核心，對數字圖像進行加密設計。外界影像首先通過傳感器轉換為符合CCIR656 協議的圖像信號，再通過EP2C35開發板上的I/O接口，以DMA方式存儲在SDRAM 中，等待Flash 中的加密程序對其處理。加密后的圖像數據通過液晶屏接口程序，由數字液晶屏接收并進行顯示。具體過程如圖1所示。

3 系統軟件設計

軟件設計的主要任務是對存儲在SDRAM中的圖像數據進行加密處理。首先為了防止在讀取圖像數據時發生沖突，要在SDRAM 中申請一個用來采集輸入，一個用來顯示輸出的兩個幀緩存區（640×480×2×8=4.915 2M幀）。當圖像數據讀入后，由保存在Nios II 軟核處理器中的加密算法對其進行加密，接到輸出指令后，進行輸出，在液晶屏上顯示密圖。整個過程只要有圖像數據輸入就會不斷進行下去。

在Nios II IDE下編輯的基于Arnold變換和騎士巡游變換相結合的復合置亂算法關鍵加密代碼如下：

void Arntranst（int m-Times） //Arnold 變換置亂函數

{

……//變量定義及賦值過程

for（k=1；k<=_Times；k++）

{ for（i=0； i

{ for（j=0；j

{ IpSrc = （uint8*）p_data+wide*i+j； //IpSrc為源位圖中待加密象素指針

//P_data為指向源位圖數據區首象素的指針

m=i+j；

n=i+2*j；

if（m>=wide）

m=m%wide；

if（n>=height）

n=n%height；

IpDst=（uint8 *）temp+wide*m+n；

//IpDst 為IpSrc 所指向的象素經過復合置亂算法映射后在緩沖區中的指針

*IpDst=*IpSrc；}}

memcpy（p_data，temp，wide*height）；}}

void Knight8（int m_Times1） //8*8騎士巡游置亂函數

{

……//變量定義及賦值過程

for （ k=1；k<=m_Times1；k++）

{ for （m=0；m

{ for（n=0；n

{ x=8*m；

y=8*n；

for （i=x；i

{ for （j=y； j

{ u=findrow（T，64）；

v=findcolum（T，64）；

x1=x+u；

y1=y+v；

*（uint8*）（temp+i*wide+j）=*（uint8*）（p_data+x1*wide+y1）

} } } }

memcpy（p_data，temp，wide*height）； }}

4 實驗比較

由于受目標板存儲空間的限制，本次加密只是針對256×256像素的8位灰度圖進行實驗，實驗通過改變迭帶值進行幾種置亂技術加密效果的比較。圖2是對原始圖像分別進行0、1、5、8、10次Arnold 算法的實驗結果，圖3是對原始圖像進行0、2、5、8、48次騎士巡游算法的實驗結果，圖4是對原始圖像進行0+0、1+2、5+5、8+8、10+48次復合算法的實驗結果。

從實驗效果可以看出，基于Arnold變換和騎士巡游變換相結合的復合置亂算法對圖像加密效果良好。

5 結語

本文將Arnold變換和騎士巡游變換相結合，提出一

種新的復合圖像置亂加密算法，并用目標板實現了相應的功能。在設計過程中將3種置亂算法在加密效果上進行了分析比較，結果表明，復合置亂算法無論在加密效果上還是在安全性上都得到了很大提升。但也存在一些問題亟待解決，例如彩色圖像加密、圖像解密的復雜性等問題，都有待進一步研究。

參考文獻：

[1] 張志剛.FPGA與SOPC設計教程[M].西安：電子科技大學出版社，2007.

[2] 王麗娜.網絡多媒體信息安全保密技術[M].武漢：武漢大學出版社，2003.

[3] 鄒建成，鐵小勻.數字圖像的二維 Arnold 變換及其周期性[J].北方工業大學學報，2000（1）：10-14.

[4] GL CHIA，SIEW-HUI ONG.Generalized knight's tours on rectangular chessboards[J].Discrete Applied Mathematics，2005（5）：80-98.

[5] 王建校，危建國.SOPC基礎與實踐[M].西安：電子科技大學出版社，2006.