簡化線狀要素算法實(shí)現(xiàn)及比較研究

陳炫巖+劉福江

摘 要：在GIS研究中，地圖矢量數(shù)據(jù)通常用線狀圖形表達(dá)，研究主要集中在線狀要素自動簡化模型建立上。為對比不同線狀要素簡化算法的特點(diǎn)，分別對面積和道格拉斯匹克兩種線要素簡化算法進(jìn)行了簡化，并通過橫向和縱向?qū)λ惴ㄟM(jìn)行比較。實(shí)驗(yàn)結(jié)果發(fā)現(xiàn)，道格拉斯匹克算法隨簡化率升高，保留點(diǎn)下降速率相對柔和，在相同簡化率的情況下，道格拉斯匹克算法單位長度偏移更小。因此，從整體上考慮，道格拉斯匹克算法性能更優(yōu)。

關(guān)鍵詞：制圖綜合；線狀要素簡化；基于面積的算法；道格拉斯匹克算法

DOIDOI：10.11907/rjdk.172089

中圖分類號：TP312

文獻(xiàn)標(biāo)識碼：A 文章編號文章編號：1672-7800（2017）008-0029-03

0 引言

空間數(shù)據(jù)多尺度表達(dá)問題是GIS研究的重點(diǎn)，也是地圖自動綜合的瓶頸。地圖矢量數(shù)據(jù)都可用線狀圖形來表達(dá)，這就使多尺度研究的焦點(diǎn)主要集中在線要素自動簡化模型的建立上。許多學(xué)者已經(jīng)對此問題作了大量研究，Douglas DH和Peucker TK[1]提出DP算法，其采用首尾相連進(jìn)行迭代化簡；Li Zhi-lin和Openshaw[2]提出基于客觀綜合的自然規(guī)律的線劃要素化簡的方法；VisvaLingam 和Whyatt[3]提出基于最小面積的重復(fù)式點(diǎn)刪除方法；Salfeld[4]提出基于邏輯一致的Douglas算法；郭慶勝[5]提出漸進(jìn)式化簡算法；武芳[6]提出面向地圖基于遺傳算法的線要素化簡算法等。線簡化算法種類繁多[7-8]，本文以道格拉斯匹克（DP）算法和最小面積算法為例，縱向研究每種算法的簡化特點(diǎn)，并橫向比較兩種算法的優(yōu)劣。

1 算法概述

1.1 基于面積的線要素簡化

迭代計(jì)算相鄰3點(diǎn)圍成面積，如果大于先前設(shè)定的面積，則保留這3個(gè)點(diǎn)，并向下遍歷；若小于先前設(shè)定的面積，則刪除中間的點(diǎn)，繼續(xù)向下遍歷選點(diǎn)，直至遍歷整條線段。

1.2 道格拉斯匹克線要素簡化

先選擇首尾兩點(diǎn)連接，遍歷兩點(diǎn)之間的所有點(diǎn)，找到距離首尾連線垂距最大的點(diǎn)，若最大垂距小于設(shè)定閾值，則刪除中間的所有點(diǎn)；若最大垂距大于設(shè)定閾值，則保留此點(diǎn)，并將其與首尾相連，得到兩根新的線段。分別對新線段進(jìn)行如上操作，直至判斷完整個(gè)曲線上的點(diǎn)。

2 研究方法及技術(shù)路線

首先明確線狀要素簡化的原因，是為了滿足不同比例尺下的地圖信息表達(dá)[9-10]。首先明確一個(gè)概念——簡化率，因?yàn)榫€狀要素簡化的方法是先將其降維，轉(zhuǎn)化為一系列離散的點(diǎn)狀要素，再合理選取這些描述線要素的點(diǎn)要素，重新形成簡化后的線要素。所以，簡化率定義為：

α=Ndelete/Nsum（1）

其中，α為簡化率，Ndelete為刪除的點(diǎn)數(shù)，Nsum為簡化前的總點(diǎn)數(shù)。

另外，在不同比例尺下，盡管是同一條線段，也要用不同數(shù)量的點(diǎn)對其進(jìn)行描述，即地圖綜合。所以，假設(shè)曲線原圖比例尺為1：n，簡化前的總點(diǎn)數(shù)為Nsum，若要轉(zhuǎn)換到1：N比例尺下，應(yīng)該保留的點(diǎn)數(shù)Nreserve為：

Nreserve=nN×Nsum（2）

又有：

Ndelete=Nsum-Nreserve（3）

所以：

Ndelete=Nsum×1-nN（4）

又有：

α=Ndelete/Nsum（5）

所以：

α=1-nN（6）

基于以上公式，首先縱向評估每種算法在不同簡化率下的化簡效果，得到對應(yīng)的閾值和保留點(diǎn)數(shù)Nreserve的對應(yīng)關(guān)系，在Excel中擬合曲線，得到兩者之間的函數(shù)關(guān)系，進(jìn)而得到閾值與比例尺之間的函數(shù)關(guān)系，定量描述出兩種簡化算法的簡化特點(diǎn)。至此，可以實(shí)現(xiàn)在比例尺無級縮放條件下的閾值選擇。

另一方面，橫向?qū)Ρ葍煞N方法，在同樣的簡化率下，用兩種方法分別對同一條曲線進(jìn)行簡化，得到簡化后的曲線。將簡化后的曲線和原曲線在ArcGIS中打開，計(jì)算出相交面積，通過控制簡化率一致，從面積差異來對比評估兩種方法的簡化效果。

3 簡化結(jié)果縱向分析

3.1 基于面積的線要素簡化

3.1.1 實(shí)驗(yàn)數(shù)據(jù)及流程

選取一條初始點(diǎn)數(shù)為164的曲線作為實(shí)驗(yàn)數(shù)據(jù)，將其坐標(biāo)值導(dǎo)入.txt文件，使用C++程序讀入文件，經(jīng)過簡化算法后輸出到.txt文件，再導(dǎo)入Excel中畫出曲線。

3.1.2 簡化結(jié)果

選取不同閾值，得到不同保留結(jié)果，計(jì)算出簡化率，進(jìn)而求出相應(yīng)的比例尺分母放大倍數(shù)，即找到此方法閾值對應(yīng)的縮放尺度。另外，得到設(shè)定閾值和保留點(diǎn)數(shù)的對應(yīng)關(guān)系后，根據(jù)對應(yīng)關(guān)系產(chǎn)生的散點(diǎn)，在Excel中使用冪函數(shù)進(jìn)行擬合，顯示擬合方程，即可得到由離散點(diǎn)到連續(xù)化的映射，從而得到比例尺無級縮放條件下對應(yīng)的簡化閾值。

基于以上對應(yīng)關(guān)系，得到設(shè)定閾值與保留點(diǎn)數(shù)之間的散點(diǎn)關(guān)系，在Excel中將散點(diǎn)進(jìn)行擬合，得到初步的連續(xù)函數(shù)。在此函數(shù)中，即可得到比例尺無級變化下對應(yīng)的閾值。此函數(shù)關(guān)系為：

y=2 125.1x-0.396（7）

相關(guān)系數(shù)為：

R2=0.993 7

可以發(fā)現(xiàn)，在基于面積的線要素簡化方法中，保留函數(shù)與冪函數(shù)相近，在初期保留點(diǎn)數(shù)下降較快，但是隨著閾值不斷增大，保留點(diǎn)數(shù)緩慢收斂于2，即首尾兩點(diǎn)，相應(yīng)函數(shù)表達(dá)式如上文所示。

3.2 基于道格拉斯匹克的線要素簡化

3.2.1 實(shí)驗(yàn)數(shù)據(jù)及流程

數(shù)據(jù)及流程同3.1.1，采用同一根線控制變量，研究簡化特點(diǎn)。

3.1.2 簡化結(jié)果

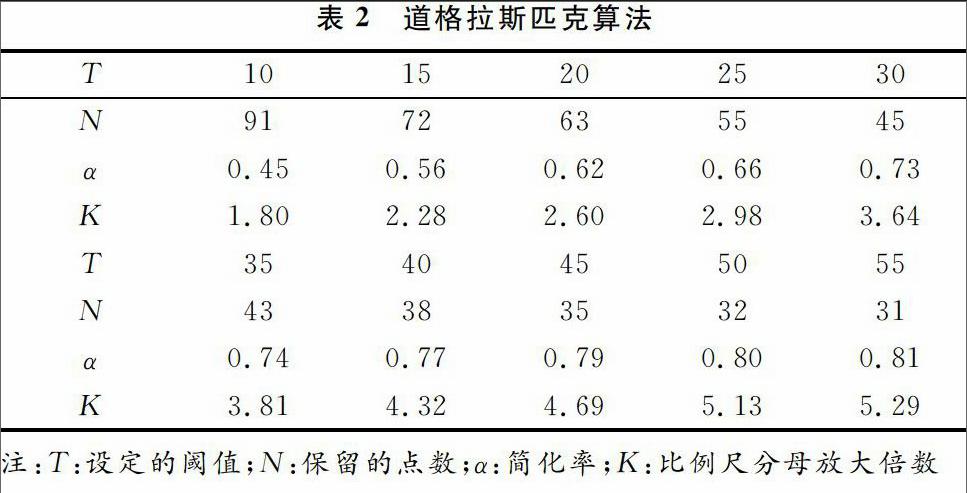
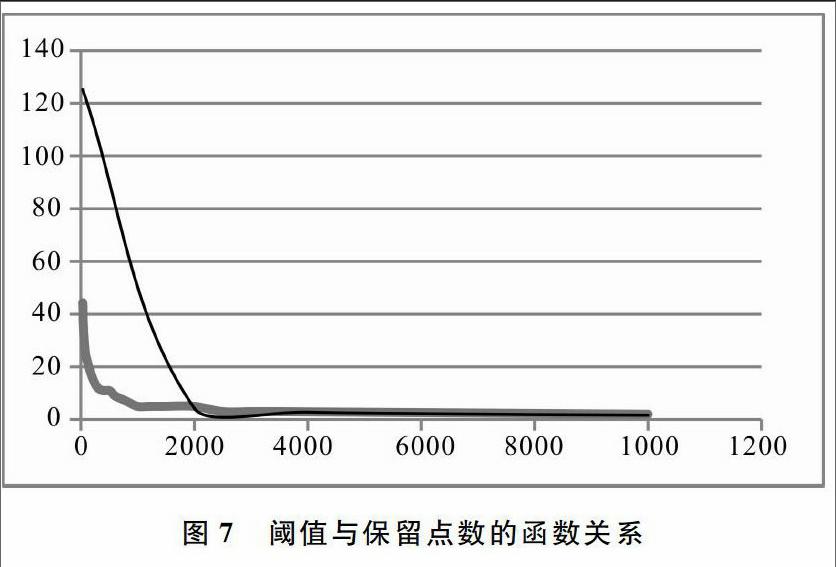
基于以上對應(yīng)關(guān)系，同樣可以得到在道格拉斯匹克算法下設(shè)定閾值與保留點(diǎn)數(shù)之間的散點(diǎn)關(guān)系。在Excel中將散點(diǎn)擬合，得到初步的連續(xù)函數(shù)，此函數(shù)關(guān)系為：endprint

y=317.31x-0.57（8）

相關(guān)系數(shù)為：

R2=0.993 1

對比基于面積的線簡化算法，道格拉斯匹克算法的保留函數(shù)柔和很多，下面分析兩種保留函數(shù)保留點(diǎn)數(shù)下降的速率。

分別對兩個(gè)保留函數(shù)求導(dǎo)，得到其導(dǎo)函數(shù)，可知導(dǎo)函數(shù)為其簡化速率。兩者相除，則可知簡化速率的相對倍數(shù)。

基于面積的簡化方式的簡化速率為：

v1=-841.539 6x-1.396（9）

基于道格拉斯匹克算法的簡化方式的簡化速率為：

v2=180.900 9x-1.57（10）

所以，面積簡化算法的簡化速率為DP算法的v1/v2倍：

v1v2=4.651 9x0.174（11）

4 簡化結(jié)果橫向分析

選擇簡化率為80%的兩種算法進(jìn)行簡化結(jié)果的橫向比較分析。基于面積的簡化線閾值為40，簡化率為80%，保留點(diǎn)數(shù)為32；基于道格拉斯匹克的簡化線閾值為50，簡化率為80%，保留點(diǎn)數(shù)為32。

將簡化結(jié)果與源數(shù)據(jù)相交，求得相交的面積區(qū)域總和。統(tǒng)計(jì)結(jié)果為40個(gè)相交區(qū)域，面積最大值為49 918.111 021，面積最小值為49.419 953，面積總和為479 090.813 592，單位長度面積偏移量為20.020 091 4。

同理，將基于道格拉斯匹克算法的簡化結(jié)果與源數(shù)據(jù)相交，求得相交的面積區(qū)域總和。統(tǒng)計(jì)結(jié)果為56個(gè)相交區(qū)域，面積最大值為62 933.889 761，面積最小值為15.621 068，面積總和為330 143.467 505，單位長度面積偏移量為13.795 928 05。

以下定量比較兩種方法的簡化效果，統(tǒng)計(jì)結(jié)果如表3所示。

經(jīng)過分析對比可以得到，當(dāng)線簡化的簡化率相同時(shí)，基于面積簡化的效果不如基于道格拉斯匹克算法簡化的結(jié)果。可以從單位長度面積偏移量對比，也可以從相交區(qū)域的面積總和值進(jìn)行對比。但是從最大值和最小值的角度來看，基于面積的算法是從局部進(jìn)行簡化的，而道格拉斯匹克算法是從空間分布整體進(jìn)行簡化的。因此，基于道格拉斯匹克算法的Max值大于基于面積算法的Max值。

5 結(jié)語

由分析結(jié)果可以得到，基于面積簡化的偏移面積總和與基于道格拉斯匹克算法的簡化線的偏移面積總和之差為：

△Sum=Sum（Area）-Sum（DP）

當(dāng)兩個(gè)算法簡化率相同時(shí)，可通過計(jì)算面積之差來比較簡化效果。這里選擇簡化率為80%時(shí)的面積數(shù)據(jù)，得到△Sum=6.224 163 4。當(dāng)簡化率相同且達(dá)到一定值時(shí)，基于面積和基于道格拉斯匹克算法的簡化面積偏移量相差并不大，但是可以定量反映出兩種簡化效果的差別。

本文通過建立每一種簡化算法對應(yīng)的閾值T和保留點(diǎn)數(shù)Nreserve的函數(shù)關(guān)系，近似擬合曲線得到一般規(guī)律。利用一般規(guī)律來確定簡化線的閾值大小，進(jìn)而確定對應(yīng)的簡化率以及縮放的比例尺等。下一步可以繼續(xù)研究當(dāng)簡化率大小不同時(shí)，兩種算法簡化面積偏移的變化，也可以繼續(xù)模擬擬合曲線，以進(jìn)一步定量研究兩種算法的優(yōu)劣。

參考文獻(xiàn)：

[1] DOUGLAS DH，PEUCKER TK.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].The CanadianCartographer，1973，10（2）：112-122.

[2] ZHILIN LI，STAN OPENSHAW.Algorithms for automated line generalization based on a natural principle of objective generalization[J].Geographical Information Systems，1992，6（5）：373-389.

[3] MVISVALINGAM，JD WHYATT.Line generalization by repeated elimination of the smallest area[J].The Cartographic Journal，1993，30（1）：46-51.

[4] SAALFELD A.Topologically consistent line simplification with the douglas-peuckeralgorithm[J].Cartography and Geographic Information Science，1999，26（1）：7-18.

[5] 郭慶勝.線狀要素圖形綜合的漸進(jìn)方法研究[J].武漢測繪科技大學(xué)學(xué)報(bào)，1998，23（1）：52-56.

[6] 武芳，錢海忠，鄧紅艷，等.面向地圖自動綜合的空間信息智能處理[M].北京：科學(xué)出版社，2008：164-170.

[7] 劉鵬程，羅靜，艾廷華，等.基于線要素綜合的形狀相似性評價(jià)模型[J].武漢大學(xué)學(xué)報(bào)信息科學(xué)版，2012，37（1）：114-117.

[8] 雷偉剛，童小華，劉大杰.基于曲線擬合的線要素綜合數(shù)據(jù)整體處理方法[J].武漢大學(xué)學(xué)報(bào)：信息科學(xué)版，2006（10）：896-899.

[9] 李霖，于忠海，朱海紅，等.地圖要素圖形沖突處理方法——以線狀要素（道路、水系和境界）為例[J].測繪學(xué)報(bào)，2015，44（5）：563-569.

[10] 鄧敏，彭東亮，徐震，等.一種基于彎曲結(jié)構(gòu)的線狀要素Morphing方法[J].中南大學(xué)學(xué)報(bào)：自然科學(xué)版，2012（7）：2674-2682.endprint