波浪誘發松散海床漸進式液化的數值分析

欒一曉

(1. 武漢理工大學，湖北 武漢 430070)

波浪誘發松散海床漸進式液化的數值分析

欒一曉1

(1. 武漢理工大學，湖北 武漢 430070)

近海區域廣泛分布著第四紀新沉積的松散海洋土，波浪荷載作用下松散海床會發生液化進而對近海結構物的穩定性存在巨大威脅。本文采用中國科學院流體-結構-海床相互作用數值計算模型FSSI-CAS 2D，選用Pastor-Zienkiewicz-Mark Ⅲ(PZⅢ)彈塑性本構研究了波浪誘發的松散海床液化問題。分析了波浪荷載引起的松散海床內超孔隙水壓力、有效應力以及應力角的時程變化特性，并預測了松散海床的漸進液化過程。計算結果表明，波浪荷載作用下松散海床內殘余孔壓會累積增長，海床表面最先發生液化，然后逐漸向下發展至液化最大深度。同時指出海床內超孔隙水壓力的豎向分布特征和應力角的變化時程均可以作為判斷海床液化的間接參數。最后，通過應力狀態分析，討論了海床漸進式液化的發展過程和趨勢。

漸進式液化；松散海床；波浪荷載；FSSI-CAS 2D；PZⅢ本構模型

1 引言

波浪荷載作用下海洋結構物的穩定性是工程設計中需要重點考慮的問題之一。近海廣泛存在著松散的第四紀新沉積海洋軟土，當遭遇較大波浪荷載時，土體顆粒會伴隨著孔隙水的排出而重新排列，海床變得更為密實，過程中超孔隙水壓力會逐步累積，海床土體的塑性變形會累積增大，引起海床液化進而導致地基承載力不足造成海洋結構物失穩破壞。因此海床在波浪荷載作用下的動態響應是評價服役期內離岸結構物穩定性的重要因素，而目前對波浪荷載作用下海床內超孔隙水壓力的增長模式以及海床的液化機理尚揭示不足，迫切需要針對該問題開展研究工作。

針對波浪-海床相互作用問題已有大量研究成果，最先是基于Biot理論提出的解析解分析模型[1]，但該分析方法的局限在于假定海床是十分密實的土體，在波浪荷載作用下主要是發生彈性變形。Lee借助耦合求解方法進一步考慮海床表面海水和海床內孔隙水的物質交換及壓力傳遞連續條件分析了波浪和海床的相互作用[2]，但僅限于自由海床的分析，尚無法用于分析上覆有結構物工況時海床的動態響應。

除解析解外，數值計算分析在研究波浪作用下海床的動力響應方面取得了重要突破。早期的數值模擬仍采用彈性本構方程，同時假定海床處于密實狀態[3]，實際上海洋工程結構物的設計中應更多考慮新沉積的松散海洋土，采用更為先進的本構模型來描述海洋土的非線性和彈塑性。在已有的數值研究成果中，主要分為兩類研究方法。第一類方法主要是通過循環荷載周次來表征海床發生液化時土所承受的剪應力，如Seed等[4-5]通過土工實驗數據建立了剪切應力比和破壞周數的關系。但該類方法中的剪應力大都是基于多孔彈性理論求解，所求得的剪應力幅值是恒定不變的，無法反映松散海床中隨著孔隙水壓力的累積剪應力逐漸減小直至伴隨著土體的液化最終為零的物理現象，從而嚴重高估了波浪的動荷載效應。第二類方法是應用彈塑性本構模型來考察松散海床的非線性動力響應。Sassa等[6]基于兩層流和移動邊界理論，提出孔壓預測模型的主要思路是認為循環荷載作用下塑性體應變的變化率依賴于剪切應力比與最終應變狀態的乘積，其預測結果與試驗結果吻合很好，但尚無法得到松散海床內不同位置的有效應力。2006年，Dunn等[7]應用Pastor等[8]和Zienkiewicz等[9]提出的Pastor-Zienkiewicz Mark-Ⅲ (PZⅢ)模型，研究了漸進波作用下埋置管線周圍的松散海洋土的液化情況。Jeng和Ou[10-11]將PZⅢ模型從二維擴展到了三維，但已有研究成果還不足以深入地揭示松散海床土體在波浪荷載作用下的液化規律。

本研究采用FSSI-CAS 2D[12]數值計算模型對新沉積的松散海床土體在波浪荷載作用下的液化規律做進一步的研究和探討。數值模型中采用PZⅢ彈塑性本構模型，計算過程中孔隙率及相應的滲透系數隨著波浪荷載的動態作用而發生的實時變化，通過實時更新剛度矩陣來反映海洋土在循環荷載作用下的非線性動力特性。研究結果表明，基于FSSI-CAS 2D模型的數值分析可以相對有效地反映松散海床在波浪荷載作用下的動力響應特征，通過對松散海床內超孔隙水壓力、有效應力以及應力角的時程變化特性的分析，提出了判斷海床液化的間接依據，并預測了波浪誘發海床漸進式液化的發展過程。

2 數值模型和土體本構

應用Zienkiewicz等[9]、Biot[1]和Chan[13]提出的u-p格式動力Biot方程作為控制方程，模擬波浪荷載作用下多孔介質海床的動態響應：

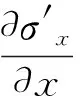
(1)

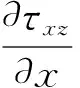
(2)

k2ps-γwnβ+kρf=γw，

(3)

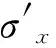
(4)

式中，Sr為海床土體飽和度；pw0為靜水壓力的幅值；Kf為孔隙水的體積模量，通常取值為2.24×109N/m2；孔隙液體壓縮性β反映了海床土體的不飽和程度。實際上，在近海岸區域海床土體的飽和度一般大于90%，接近于完全飽和。

應用廣義Newmark[13]法的隱式求解公式(1)至式(3)。對于波浪-結構-海床之間的相互作用問題，Ye[14]建立了耦合的數值模型FSSI-CAS 2D，模型中使用Hsu等[15]提出的Volume Average Reynold Average Navier Stokes(VARANS)方程控制波浪運動和孔隙介質中流體的流動方式，而結構物和海床的動態響應由廣義Biot動力方程控制，Ye等[14,16]和Zienkiewicz等[17]的研究成果中提供了將Biot動力方程和VARANS方程進行耦合求解的算法。

以往研究中通常基于變形較小的假設而在計算中保持孔隙比e和滲透系數k為常數。本研究中依據大變形理論提出的方程en+1=(1+en)exp(ΔpQ+Δεvs)-1考慮了海床土體的孔隙比及相應的滲透系數隨土體顆粒的變形和重組的變化，其中n表示計算的時間步，Δp為孔隙水壓力的增量，Δεvs為海洋土的體應變增量，Q=1/β為孔隙水的壓縮性。相應的，海洋土的滲透系數k可以表述為k=Cfe31+e，其中，Cf為經驗系數，取決于Cf=k01+e0e30[18]，式中e0為初始孔隙比。波浪荷載作用下松散海床會發生較大變形，海床表面的幾何形狀會發生顯著變化，因此計算中海床表面的靜水壓力和動水壓力將隨著海床表面的變形而動態改變，保證了不同時間步內計算域的力邊界條件始終實時更新，從而實現耦合求解。

在FSSI-CAS 2D數值模型中采用PZⅢ本構模型[8]描述海洋土的動力特性。PZⅢ模型作為一種彈塑性本構模型，其可靠性已經被一系列單調加載試驗、循環荷載試驗、離心模型試驗及相關工況的數值模擬結果[19]所證實。

3 驗證

2012年Ye[14]通過對比已有的數模和物模研究成果，驗證了半耦合數值計算模型FSSI-CAS 2D在預測自由海床和防波堤地基在波浪荷載作用下的動力響應方面的有效性和可靠性，如Hsu和Jeng的解析解[20]，規則波和橢圓余弦波的水槽試驗[21]，駐波[22]，半潛式防波堤[23]以及組合式防波堤[24]。隨后Ye等[25-26]進一步通過與波浪槽試驗[27]和離心模型試驗[19]的模擬，驗證了FSSI-CAS 2D計算模型在求解波浪-松散海床相互作用方面的有效性。

4 模型邊界條件和水動力荷載

計算模型為一個400 m長、20 m厚的平坦海床，其中，設置該區域的左下角點為原點。水平方向的網格尺寸為1 m，豎直方向網格尺寸為0.5 m，總共生成12 000個4節點單元。邊界條件設置如下：第一，底部邊界不允許排水；第二，兩個水平邊界的水平方向不允許有變形；第三，在海床表面施加靜水壓力。在每一個時間步，激活施加在海床的靜水壓力作為施加在海床表面的邊界數值，每一步更新公式為ps=ρgd0+ρgsv，式中，d0為初始水深，sv為波浪荷載作用下海床表面節點的豎向殘余位移和瞬間位移之和；第四，波流引起的動水壓力也作用在海床上，其三階表達式為[28]：

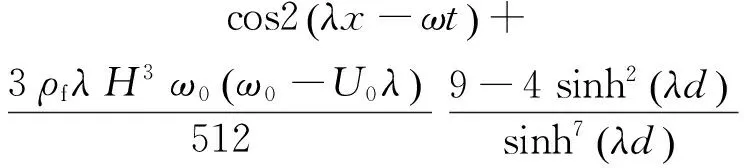
cos3(λx-ωt)，

(5)

式中，H為波浪高度；λ=L/2π為波數；L為波長；ω=T/2π為角速度；U0為當前速度；d=d0+sv為即時水深。當不考慮流U0=0 m/s時，上述方程退化為經典的三階非線性波。當在海床上施加靜水壓力和動水壓力時，海床表面土體的有效應力確保為0。

PZⅢ模型參數可以根據近海土體的室內試驗獲得，本文中采用的是相對密度為60%的Nevada砂的參數[17]，列于表1。其中初始孔隙比e=0.333，飽和度為98%。相應地，海床土體初始的滲透系數為1.0×10-5m/s，初始水深為10 m，波高為1.5 m，波浪周期為8 s，流速U0=0.5 m/s。

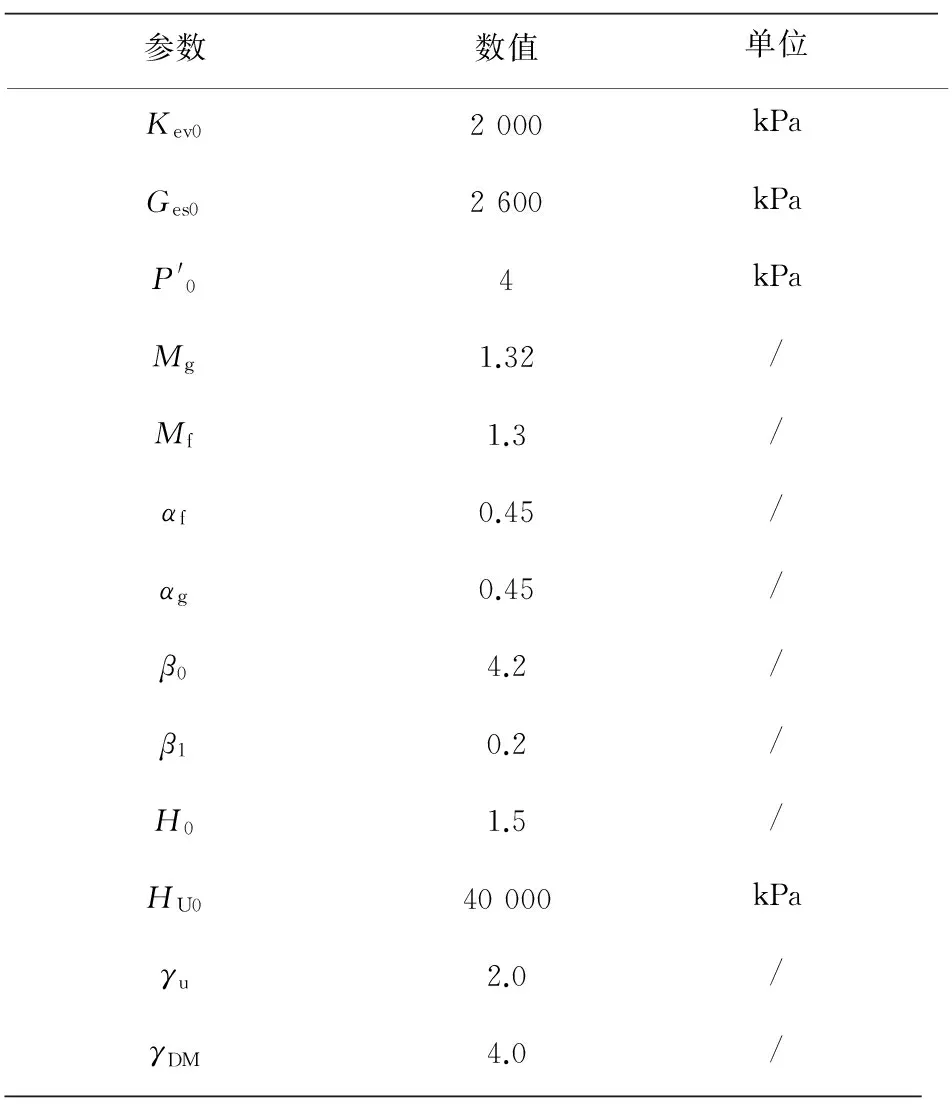
表1 PZⅢ模型中松散海床土體參數[18]

5 計算結果

在近海環境中，靜水壓力會引起海床土的長期固結，但不引起超孔隙水壓力。海床土的初始應力狀態可由Ye[29]獲得，以此開始進一步的動力分析。

5.1 有效應力和超孔隙水壓力

圖1給出了在松散海床3個典型深度處(z=18 m為在海床土體表面位置，z=10 m為海床模型的中間位置，以及z=2 m為海床底部附近位置)由波浪荷載引起的超孔壓和有效應力的時程。超孔隙水壓力由震蕩孔壓和累積孔壓兩部分組成，震蕩孔壓的幅值從海床表面向下逐漸減小，反之海床較深位置處殘余孔壓的幅值要遠大于海床表面位置，達到峰值的時間也明顯增多。波浪和海流荷載引起的累積孔壓不會無限增大，達到峰值后會保持不變。

與累積孔壓的趨勢一致，松散海床土的有效應力從初始狀態會逐漸減小，當有效應力達到0時，海床會失去抗剪強度而發生液化造成上部結構的倒塌。如圖1所示，z=18 m處土體的平均有效應力在約150 s時達到0，發生部分液化。在300 s時，有效應力變為0，意味著z=18 m處的海床表面的土體全部發生液化。在有效應力下降的過程中，剪應力的幅值也減小。當z=18 m處海床土體發生全部液化時，由波浪和海流引起的剪應力也變化為0，原因是發生完全液化的土體的性質和流體近似，不能傳遞剪應力。FSSI-CAS 2D模型可以清楚地捕捉到這樣的現象。同時也觀察到z=10 m海床中部位置土的平均有效應力沒有達到完全液化狀態。然而，與初始應力的數值相比下降超過了90%，在約300 s時發生了部分液化。z=2 m接近海床底部位置直到800 s土體也沒有發生液化。

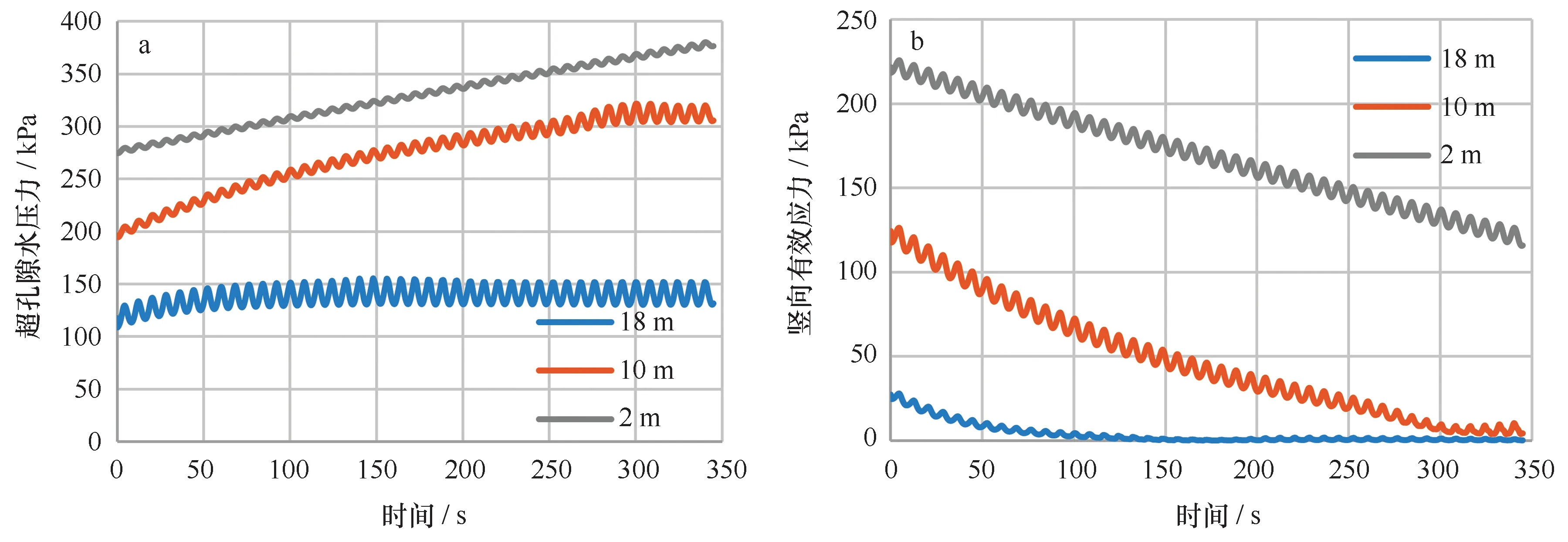
圖1 海床3個典型位置處波流荷載引發的超孔隙水壓力(a)和平均主應力(b)時程Fig.1 Time history of wave & current-induced excess pore pressure (a) and mean principle stress (b) at 3 typical depth

5.2 應力角

應力角是研究松散海床在波流荷載作用下動態響應的另一個重要參數。應力角是基于摩爾庫倫準測定義的：

(6)

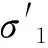
圖2為波流荷載作用下松散海床3個典型深度處的土體應力角變化時程。作為對比，也繪制出相同荷載條件下密實彈性海床土的應力角變化時程。對于密實的海床，應力角只是在初始值附近階段性地變動。然而，松散海床的應力角在初始階段逐漸減小，然后逐漸增大直到該位置土體發生部分或者完全液化，之后殘余應力角基本保持穩定。如圖2所示，在z=18 m處和在z=10 m處，兩個位置殘余應力角從增加到保持穩定的時間分別為150 s和300 s，時間與松散海床土體這兩個位置發生部分或者全部液化的時間十分一致。這說明，殘余應力角從增加到保持穩定的時間可以用來作為判斷土體發生液化的一個間接依據。

5.3 漸進式液化

室內試驗[19]和現場記錄[30]都證明松散海床在波浪荷載作用下的液化存在兩種機制。一種是瞬時液化，只發生在十分密實的土體中，另外一種是松散土體中由孔隙水壓力累積引起的殘余液化。本文研究的是發生在近海松散海床土體中的液化即為殘余液化，定義Lpotential為液化勢：

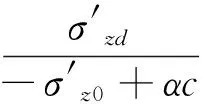
(7)

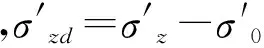
了解波浪荷載作用下松散海床中殘余孔隙水壓力沿豎向深度方向的分布特性是十分必要的。在圖3中，給出了在x=200 m處不同時間土中累積孔壓和震蕩孔壓沿豎向的分布。注意到在液化深度范圍內震蕩孔壓的豎向分布是不規則的，超出液化深度后則保持同一趨勢。因此震蕩孔壓的豎向分布可以作為液化判斷的另一個間接依據。松散海床中累積孔壓隨時間持續增長，但不會超過界限值，即液化抵抗線(LRL)，一旦到達時該位置的土體即發生液化。根據式(7)，可以估計松散海床中液化可能深度Lpotential在不同時間(如t/T=10, 20, 45)的數值，如圖4所示。圖4顯示，上層海床Lpotential比下層海床大一些，而且隨著波浪的循環加載海床的Lpotential逐漸增加達到或超過0.86而發生液化。圖3和圖4都說明，累積超孔壓達到液化抵抗線的時間隨著海床深度增加而增加，這意味著波浪荷載引起松散海床液化是一個漸進的過程，最開始是在海床表面，然后逐漸向下擴展，如圖4所示。在t=45T之后，液化深度達到11 m。

圖2 波浪荷載誘發松散海床3個典型深度處土體應力角變化時程Fig.2 Time history of wave & current-induced stress angle at 3 typical depth

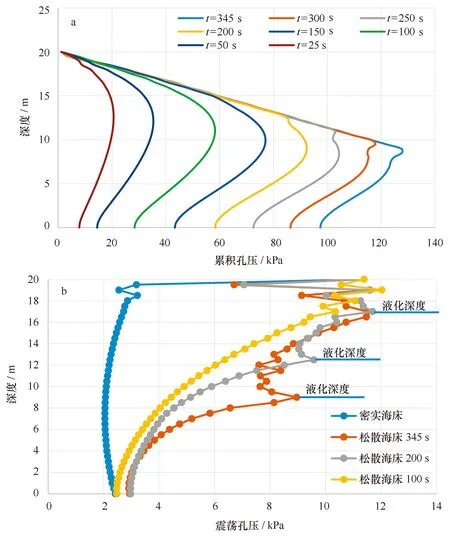
圖3 在x=200 m處不同時間土中累積孔壓(a)和震蕩孔壓(b)沿豎向的分布Fig.3 Vertical distribution of wave & current-induced residual pore pressure(a) and oscillatory pore pressure (b) on symetrical line x=200 m

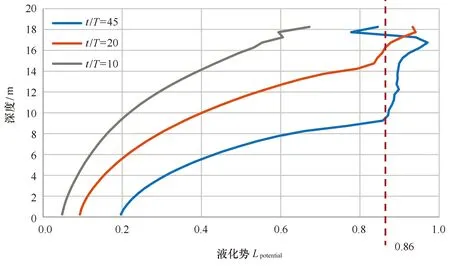
圖4 Lpotential在不同時間沿豎向的分布Fig.4 Vertical distribution of liquefaction potential Lpotential at typical time t/T=10, 20, 45

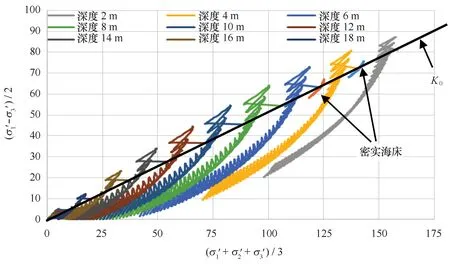
圖5 在x=200 m處不同深度位置點的應力路徑(單位：kPa)Fig.5 Stress paths of soil at a series of positions on x=200 m (unit: kPa)

圖6 典型時間步下波浪荷載誘發松散海床液化區域分布Fig.6 Wave & current-induced residual liquefaction zone in loose seabed at typical time t/T=10, 25, 50, 100

應力路徑是表征松散海床在波浪荷載作用下發生液化的另外一個重要參數。圖5給出了在x=200 m處不同深度位置點的應力路徑。可以發現，所有應力狀態在初始時刻都在原始K0線上。在波浪荷載的循環作用下，松散海床中的孔隙水壓力上升，有效應力下降。結果是，應力狀態逐漸向零應力狀態靠近，即為液化狀態。在計算的結尾，在x=200 m處的一系列位置的應力狀態達到了零應力狀態，發生了部分或者完全液化。

如圖6所示，通過Lpotential對整個海床的液化區域分布進行預測。可以看到，松散海床的液化區域隨時間逐漸增大，受波浪荷載的影響，起初液化區域是波浪形狀的，直到t/T=100，大部分松散海床發生液化。

6 結論

在近海區域內廣泛分布著第四紀新沉積的松散海洋土，波浪荷載引起的松散海床液化對近海結構物存在巨大的威脅。研究中，采用FSSI-CAS 2D數值計算模型，選用Pastor-Zienkiewicz-Mark Ⅲ彈塑性本構模型研究了波浪荷載誘發的松散海床液化問題。求解了典型海況下波浪荷載作用下海床的動力響應，計算結果進一步證實了波浪荷載作用下伴隨著殘余孔壓的累積松散海床的液化從海床表面開始，逐步向海床深部方向發展直至達到液化深度。結果表明可以根據震蕩孔壓的豎向分布、應力角的時程作為判斷海床發生液化或預測液化深度的間接依據。最后，通過應力狀態分析，討論了海床漸進式液化的發展過程和趨勢。研究結果可為近岸海洋結構物的設計提供技術參考。

[1] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Part 1: Low frequency range[J]. Acoustical Society of America, 1956, 28(2): 168-179.

[2] Lee T C, Tsai C P, Jeng D S. Ocean wave propagating over a porous seabed of finite thickness[J]. Ocean Engineering, 2002, 29(12): 1577-1601.

[3] Jeng D S. Wave-induced sea floor dynamics[J]. Applied Mechanics Reviews, 2003, 56(4): 407-429.

[4] Seed H B, Martin P O, Lysmer J. Pore-water pressure changes during soil liquefaction[J]. Journal of Geotechnical Engineering ASCE, 1976, 102(4): 323-346.

[5] Seed H B, Rahman M S. Wave-induced pore pressure in relation to ocean floor stability of cohesionless soils[J]. Marine Geotechnology, 1978, 3(2): 123-150.

[6] Sassa S, Sekiguchi H, Miyamoto J. Analysis of progressive liquefaction as a moving boundary problem[J]. Géotechnique, 2001, 51(10): 847-857.

[7] Dunn S L, Vun P L, Chan A H C, et al. Numerical modeling of wave-induced liquefaction around pipelines[J]. Journal of Waterway, Port, Coastaland Ocean Engineering, 2006, 132(4): 276-288.

[8] Pastor M, Zienkiewicz O C, Chan A H C. Generalized plasticity and the modelling of soil behaviour[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1990, 14(3): 151-190.

[9] Zienkiewicz O C, Chang C T, Bettess P. Drained, undrained, consolidating and dynamic behaviour assumptions in soils[J]. Géotechnique, 1980, 30(4): 385-395.

[10] Jeng D S, Ou J. 3D models for wave-induced pore pressures near breakwater heads[J]. Acta Mechanica, 2010, 215(1/4): 85-104.

[11] Ou J. Three-dimensional numerical modelling of interaction between soil and pore fluid[D]. Birmingham, UK: Universtity of Birmingham, 2009.

[12] 王良民, 葉劍紅, 朱長歧. 近海欠密實砂質海床內波致漸進液化特征研究[J]. 巖土力學, 2015, 36(12): 3583-3588.

Wang Liangmin, Ye Jianhong, Zhu Changqi. Investigation on the wave-induced progressive liquefaction of offshore loosely deposited sandy seabed[J]. Rock and Soil Mechanics,2015, 36(12): 3583-3588.

[13] Chan A H C. A unified finite element solution to static and dynamic problems of geomechanics[D]. Swansea Wales: University of Wales, 1988.

[14] Ye J H. Numerical analysis of wave-seabed-breakwater interactions[D]. Dundee, UK: Universtity of Dundee, 2012.

[15] Hsu T J, Sakakiyama T, Liu P L F. A numerical model for wave motions and turbulence flows in front of a composite breakwater[J]. Coastal Engineering, 2002, 46(1):25-50.

[16] Ye J H, Jeng D S, Wang R, et al. Validation of a 2D semi-coupled numerical model for Fluid-Structures-Seabed Interaction[J]. Journal of Fluids and Structures, 2013, 42(4): 333-357.

[17] Zienkiewicz O C, Chan A H C, Pastor M, et al. Computational Geomechanics with Special Reference to Earthquake Engineering[M]. Chichester: John Wiley & Sons Ltd, 1999.

[18] Miyamoto J, Sassa S, Sekiguchi H. Progressive solidification of a liquefied sand layer during continued wave loading[J]. Géotechnique, 2004, 54(10): 617-629.

[19] Sassa S, Sekiguchi H. Wave-induced liquefaction of beds of sand in a centrifuge[J]. Géotechnique, 1999, 49(5): 621-638.

[20] Hsu J R, Jeng D S. Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1994, 18(11): 785-807.

[21] Lu H B. The research on pore water pressure response to waves in sandy seabed[D]. Changsha: Changsha University of Science & Technology, 2005.

[22] Tsai C P, Lee T L. Standing wave induced pore pressure in a porous seabed[J]. Ocean Engineering, 1995, 22(6): 505-517.

[23] Mizutani N, Mostarfa A, Iwata K. Nonliear regular wave, submerged breakwater and seabed dynamic interaction[J]. Coastal Engineering, 1998, 33(2/3): 177-202.

[24] Mostafa A, Mizutani N, Iwata K. Nonlinear wave, composite breakwater, and seabed dynamicinteraction[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, ASCE, 1999, 25(2): 88-97.

[25] Ye J H, Jeng D S, Wang R, et al. Numerical simulation of wave-induced dynamic response of poro-elasto-plastic seabed foundation and composite breakwater[J]. Applied Mathematical Modeling, 2015, 39(1): 322-347.

[26] Ye J H, Wang G. Seismic dynamics of offshore breakwater on liquefiable seabed foundation[J]. Soil Dynamics and Earthquake Engineering, 2015, 76: 86-99.

[27] Teh T C, Palmer A C, Damgaard J S. Experimental study of marine pipelines on unstable and liquefied seabed[J]. Coastal Engineering, 2003, 50(1/2): 1-17.

[28] Ye J H, Jeng D S. Response of porous seabed to nature loadings: Waves and currents[J]. Journal of Engineering Mechanics, ASCE, 2012, 138(6): 601-613.

[29] Ye J H. Numerical modelling of consolidation of 2-D porous unsaturated seabed under a composite breakwater[J]. Mechanika, 2012, 18(4): 373-379.

[30] Sassa S, Takayama T, Mizutani M, et al. Field observations of the build-up and dissipation of residual porewater pressures in seabed sands under the passage of stormwaves[J]. Journal of Coastal Research, 2006, 39(12): 410-414.

[31] Ishihara K. Liquefaction and flow failure during earthquakes[J]. Géotechnique, 1993, 43(3): 351-451.

[32] Wu J, Kammaerer A M, Riemer M F, et al. Laboratory study of liquefaction triggering criteria[C]// Proceedings of 13th World Conference on Earthquake Engineering. Vancouver, British Columbia, Canada. 2004.

Wave-induced progressive liquefaction in loosely deposited seabed

Luan Yixiao1

(1.WuhanUniversityofTechnology,Wuhan430070,China)

Quaternary newly deposited loose seabed soil widely distributes in offshore area in the world. Wave-induced residual liquefaction in loose seabed floor brings great risk to the stability of offshore structures in extreme climate. In this study, wave & current-induced residual liquefaction in loose seabed floor has been investigated comprehensively adopting FSSI-CAS 2D incorporating Pastor-Zienkiewicz-Mark Ⅲ(PZⅢ) soil model which is a validated integrated numerical model. The time history of wave & current-induced pore pressure, effective stress, stress angle are discussed. The variation process of progressive liquefactionis illustrated in detail. The computational results confirm that the wave & current-induced liquefaction in loose seabed soil is progressively downward, initiating at seabed surface. Besides, it is found that vertical distribution of oscillatory pore pressure, and time history of stress angle could be taken as indirect indicator to judge the occurrence of wave-induced residual liquefaction. The developing process of the progressive liquefaction is analyzed by stress statement data of seabed soil.

progressive liquefaction; loose seabed floor; wave loading; FSSI-CAS 2D; PZⅢ soil model

10.3969/j.issn.0253-4193.2017.09.010

2017-06-12；

2017-08-05。

欒一曉(1996—)，女，山東省招遠市人，主要從事士力學數值模擬。E-mail：lyx1996yx@126.com

TU431

A

0253-4193(2017)09-0101-09

欒一曉. 波浪誘發松散海床漸進式液化的數值分析[J]. 海洋學報, 2017, 39(9): 101-109,

Luan Yixiao. Wave-induced progressive liquefaction in loosely deposited seabed[J]. Haiyang Xuebao, 2017, 39(9): 101-109, doi:10.3969/j.issn.0253-4193.2017.09.010