羊毛纖維集合體的分形結構與其保暖性的關系

楊 樹， 李瑪莎

(嘉興學院 南湖學院， 浙江 嘉興 314000)

羊毛纖維集合體的分形結構與其保暖性的關系

楊 樹， 李瑪莎

(嘉興學院 南湖學院， 浙江 嘉興 314000)

針對羊毛纖維集合體結構特征往往難以得到有效表征這一問題，將分形的概念引入羊毛纖維集合體的結構表征，利用計盒維數的方法，計算了5種不同質量的羊毛纖維集合體的分形維數，同時采用平板式保溫儀測定了羊毛纖維集合體的保暖性能；隨后定量關聯了羊毛纖維集合體的分形維數與其基本結構參數和保暖性指標之間的關系。結果表明：利用分形維數來表征纖維集合體的結構特征是可行的，隨羊毛纖維質量和體積分數的增大，集合體的分形維數增大，這說明集合體中的纖維結構更雜亂；隨分形維數增大，集合體的克羅值和保溫率增大，而傳熱系數減小，即纖維集合體的保暖性增強。

羊毛纖維； 集合體； 計盒法； 分形維數； 保暖性能

分形理論是20世紀后快速發展起來的重要學科之一，用于研究自然界非線性過程所具有的特殊規律性，是描述無序結構特征的有效方法。近幾年，分形方法被廣泛應用于紡織科學，包括纖維、紗線、織物、纖維集合體等不同領域[1-2]。如在纖維領域，高緒珊等[3]總結了近年來美國和日本對纖維分形結構的研究指出，纖維表面凹凸構造的自相似性與大自然的色光存在對應關系；而在紗線領域，歐健文等[4]將分形理論應用于羊毛紗線的定形，隨纖維定形時間的增長，紗線的分形維數增大，紗線結構趨于均勻，并且彈性回復率得到提高，這一結果表明羊毛纖維分形結構的研究對紡織品生產和質量提高具有重要的意義；在織物方面，吳曉晨[5]闡述了分形理論在羊絨織物數碼印花等方面的應用。

除纖維、紗線和織物外，纖維集合體如保暖絮片等的結構雜亂無章，但分形學為研究其結構提供了新的、有效的途徑。高晶等[6]運用這一特征將纖維復雜的結構簡單化，探究了纖維集合體內部的孔隙率、孔洞大小、孔洞分布以及外界條件對分形維數的影響；Fan等[7]通過計算羊毛纖維集合體的分形維數，指出其接近黃金分割點的維數是羊毛具有出色保暖性的原因；本文作者在前期研究中也通過計算非織造布的孔洞面積分形維數，建立起分形維數與其孔洞特征和吸音隔聲性能的關系[8]。

針對保暖絮片中常見的羊毛纖維集合體的結構和熱學性能的關系，本文引入分形維數的概念，利用計盒維數法計算了5種不同質量的羊毛纖維集合體的分形維數，同時采用平板式保溫儀測定了羊毛纖維集合體的保暖性能。隨后定量關聯了羊毛纖維集合體的分形維數與其基本結構參數和保暖性指標之間的關系。

1 羊毛纖維集合體的分形維數

1973年，美國哈佛大學教授Mandelbrot[9]提出了分形這一概念。分形是對具有統計意義下自相似性[10]的圖形、結構或現象的總稱，并以數學的形式予以表達。目前關于分形維數的定義主要有豪斯道夫維數、相似維數[11]、信息維數以及容量維數等。本文采用相似維數來定量分析羊毛纖維的內部結構。計算纖維集合體分形維數的具體方法為：首先對羊毛纖維進行圖像采集，經過一系列圖像處理如圖像灰度化、均勻直方圖、中值濾波、設定閾值等，得到二值化圖像；隨后通過MatLab程序[12]計算出羊毛的分形維數。

1.1 纖維集合體圖像采集

羊毛纖維為美利奴細羊毛，由嘉興市吉創紡織品有限公司提供，線密度為11.8 dtex，纖維密度為1.3 g/cm3。將羊毛纖維填塞進邊長(a)為 30 cm 的正方形模具中，采用YG141 N型數字式織物厚度儀測量纖維集合體的厚度(h)為7.5 mm。以此標準制作5份體積相同、質量不等的羊毛纖維集合體，每份集合體制作10個相同的樣品，以便后續測試計算平均結果。根據下式計算纖維集合體的體積分數：

式中：mf為纖維質量；ρf為纖維密度；a為纖維集合體的邊長；h為纖維厚度；V為體積分數。

5種纖維集合體的質量和體積分數計算結果如表1所示。

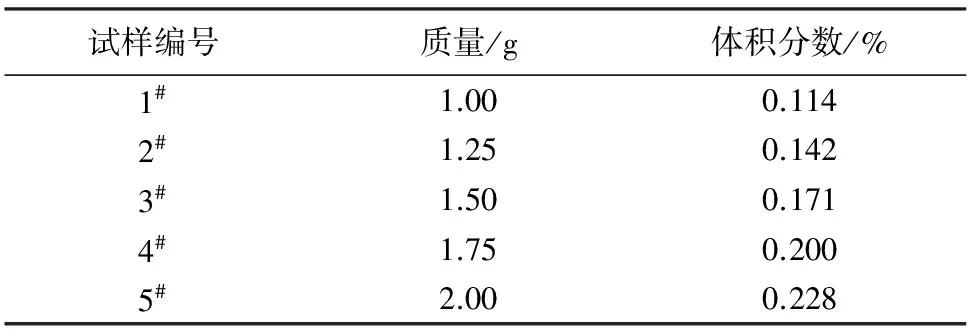
表1 羊毛纖維集合體的質量和體積分數

采用高分辨率的數碼相機對羊毛纖維集合體樣品的表面圖像進行采集，結果如圖1所示。由于纖維集合體的厚度較小，因此表面圖像也在一定程度上可反映集合體內部的結構特征。

1.2 圖像預處理

采用Photoshop軟件將圖像設置成灰度級，使圖像忽略掉其原本的彩色信息，從而達到增強對比度的效果，接著通過直方圖均勻化將圖像改為均勻直方圖分布，直方圖表示灰度級在圖像像素中的個數，增強灰度范圍，使圖像對比度更明顯，最后進行圖像中值濾波[13]確定，消除孤立的噪音點，提高圖像的質量。

1.3 圖像二值化

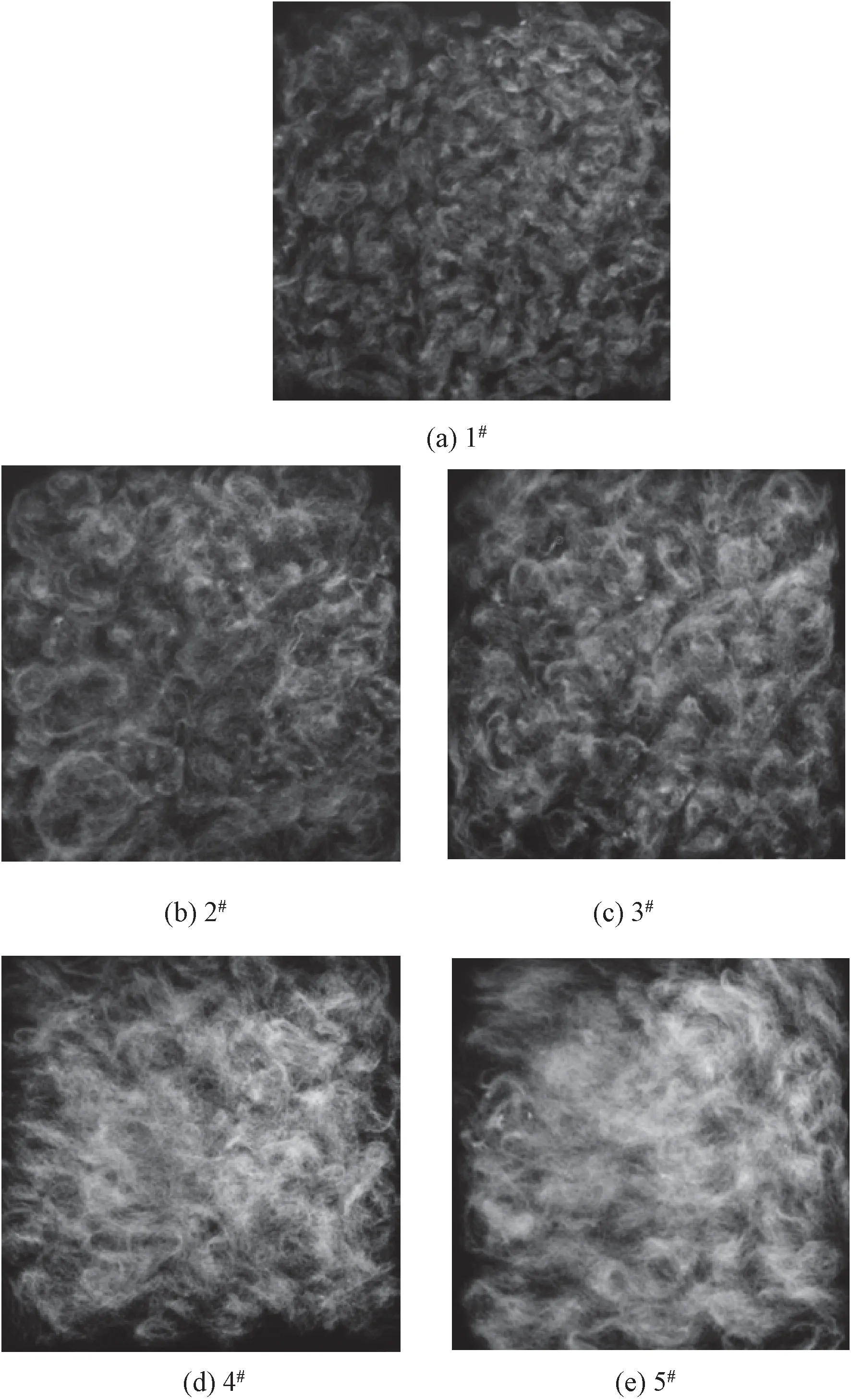
圖2 試樣照片的二值化圖像Fig.2 Image binarization of sample photos

經上述處理再確定一個閾值，并以這個閾值為極限，將多灰度級的圖像變成二灰度級的圖像，當圖像中的某像素點值大于該閾值時，將灰度值設置成255，為黑點；小于或等于這個閾值時，設置成0，即為白點，從而使圖像變成清晰的黑白圖，即二值化圖像[14]，如圖2所示。可見經處理后的圖像只存在黑白2種顏色，沒有雜色干擾，結構特征更為明顯，質量越大的纖維幾何體，其纖維間的結構更為緊密。

1.4 計算分形維數

盒維數法[15](Sandbox)是Stanley在1985年提出的，不僅適用于自相似的結構，也可用于非自相似性的結構。其計算方法是使用固定邊長正方形的盒子蓋住掃描得到的圖像，計算含有圖像纖維的格子數，記為N(?)，將?縮小一半，再重復以上步驟，即每個?對應一個N(?)值[16]。用?→0 的方法做r(N)=1/N(1/D) 和lnN(1/?)的最小二乘法擬合圖，其中D代表盒子的大小。該圖越接近于一條直線，說明分形特征越明顯，直線的斜率即為分形維數。

本文利用MatLab編寫程序計算5種羊毛纖維集合體的分形維數，計算過程中擬合的圖形接近直線，這說明樣本的分形特征較為明顯，由此得到5種試樣的計盒分形維數值，從試樣1#到5#分別為1.624、1.663、1.697、1.725和1.756。

1.5 分形維數與結構參數的關系

接下來開始建立纖維集合體的分形維數與其纖維質量、體積分數之間的關系。將羊毛纖維集合體分形維數結果與纖維質量作比較，結果如圖3所示。由圖可見，纖維分形維數與質量之間成正相關關系，纖維質量越大，分形維數越大。將羊毛纖維集合體分形維數結果與纖維體積分數作比較，得到如圖4所示的結果，R2=0.994 18，即體積分數的與分形維數的相關性是較好的，隨著纖維體積分數逐步增大，分形維數也越來越大。

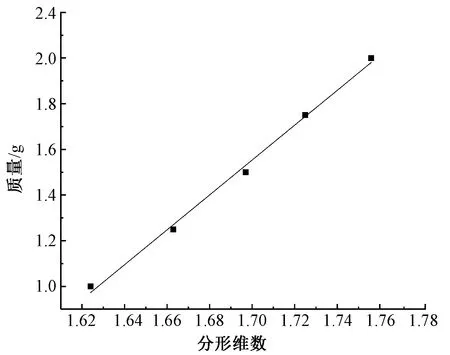
圖3 羊毛分形維數與纖維質量的關系Fig.3 Relationship between fractal dimension and mass of wool fiber

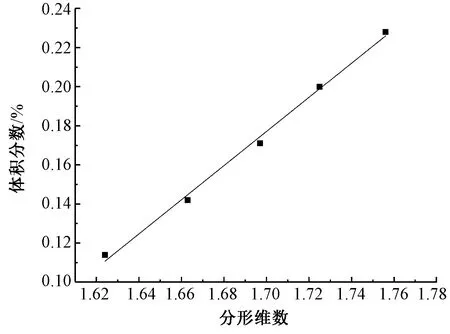
圖4 羊毛分形維數與纖維體積分數的關系Fig.4 Relationship between fractal dimension and volume fraction of wool fiber

纖維集合體的分形維數從本質上來說表達的是集合體內部的結構雜亂度，即纖維內部結構越雜亂和無序，其分形維數越大，反之亦然，隨集合體內部纖維質量和體積的增加，纖維與纖維之間的排列勢必會越來越雜亂，因此其分形維數也會增加。這也證實了分形維數可表征集合體內部結構無序度的可行性。

2 羊毛纖維集合體的保暖性能

羊毛的保暖性能主要由3種指標來表征，分別是克羅值、保溫率和傳熱系數。依據ASTM C1044—2012《使用單面護熱板設備或薄型加熱器設備的標準實施規程》，采用YG606 型平板式保暖儀進行。測試過程中首先進行空板試驗，底板的溫度設定為36 ℃，預熱時間為30 min。然后將5份試樣依次覆蓋在測試驗板上，試驗板為30 cm×30 cm的正方形，因此試樣可將試驗板完全覆蓋，將試驗板、保護板和底板都設置為相同的溫度，進行測試。測試3次后，得到3個熱學指標的平均值，結果如表2所示。

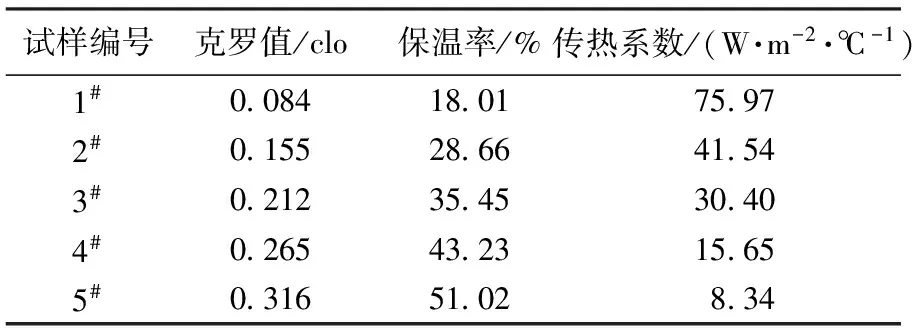
表2 試樣的保暖性能參數

3 羊毛分形維數與保暖性能的關系

圖5示出克羅值、保溫率和傳熱系數與羊毛纖維分形維數的關系。由圖5(a)可知，克羅值的大小與纖維分形維數呈正相關關系，且具有很高的相關度，可見分形維數越大，克羅值越大，即保暖性能越好。如圖5(b)所示，羊毛纖維集合體的保溫率隨分形維數的增大而增加，說明纖維集合體結構的雜亂程度增大，保暖性增強。由圖5(c)可看出，傳熱系數隨纖維分形維數的增大而減小，二者呈反相關關系，即隨著分形維數變大，纖維間傳熱速率減緩，則纖維集合體的保暖性能增加。

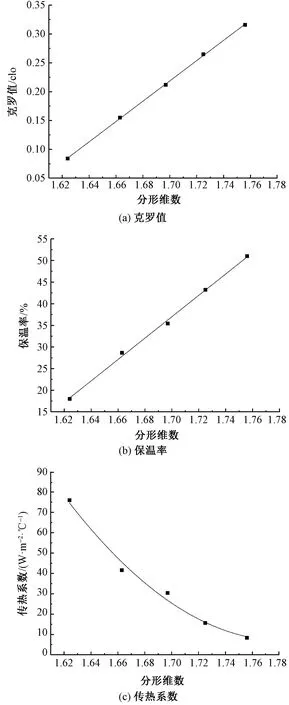
圖5 羊毛纖維分形維數與各參數之間的關系Fig.5 Relationship between fractal dimension and clo value(a), insulation rate(b) and heat transfer coefficient(c)

4 結 論

本文將分形的概念引入纖維集合體的結構表征中，利用MatLab編程計算了不同質量和體積分數的羊毛纖維集合體的分形維數，并測試了其熱學性能，建立了纖維集合體的分形維數與其結構參數和熱學指標之間的關系。

1)利用計盒法分形維數的計算方法得到羊毛纖維集合體的分形維數值發現，分形維數與其纖維質量、體積分數幾乎呈線性增大關系，說明非整數的數值可直觀反映羊毛纖維結構的雜亂程度，也表明羊毛纖維集合體內部結構具有很強的分形特征。

2)測定了不同質量的羊毛纖維集合體的保暖性能，并建立了其保暖性指標和分形維數之間的關系發現，隨著纖維集合體分形維數的增大，其克羅值和保溫率也隨之增大，而傳熱系數減小，即整體上保暖性能增強。

[1] 朱志寶, 白永強. 分形幾何及其應用[J]. 價值工程, 2012, 31(35): 5-7. ZHU Zhibao, BAI Yongqiang. Fractal geometry with its application[J]. Value Engineering, 2012, 31(35): 5-7.

[2] 王海毅, 田耀斌, 鄭新苗. 基于分形理論的微纖維玻璃棉絕熱紙的結構與性能研究[J]. 陜西科技大學學報(自然科學版), 2016, 34(5): 1-4. WANG Haiyi, TIAN Yaobin, ZHENG Xinmiao. The study on structure and performance of micro fiber glass paper based on fractal theory[J]. Journal of Science and Technology in Shanxi University (Nature Science Edition)， 2016,34(5):1-4.

[3] 高緒珊, 莊毅. 天然纖維的分形結構和分形結構纖維的開發[J]. 合成纖維工業, 2000, 23(4): 35-38. GAO Xushan, ZHUANG Yi. Fractal structure of natural fiber and exploitation of fiber composed with fractal [J]. Synthetic Fiber Industry, 2000, 23(4): 35-38.

[4] 歐健文, 姚金波, 李淑紅, 等. 分形理論在羊毛紗線定形中的應用[J]. 紡織學報, 2011, 32(5):33-37. OU Jianwen, YAO Jinbo, LI Shuhong, et al. Application of fractal theory in wool yarn setting[J]. Journal of Textile Research, 2011, 32(5): 33-37.

[5] 吳曉晨. 基于分形學的羊絨織物數碼印花仿扎染圖案設計研究[D]. 呼和浩特：內蒙古工業大學, 2014：3-4. WU Xiaochen. The study of digital print of cashmere based on fractal theory[D]. Hohhot:Inner Mongolia University of Technology, 2014:3-4.

[6] 高晶, 于偉東, 潘寧. 羽絨纖維及其集合體結構和性能的研究[D]. 上海:東華大學,2006: 5-7. GAO Jing, YU Weidong, PAN Ning. Study on structure and property of eiderdown[D]. Shanghai: Donghua University, 2006: 5-7.

[7] FAN J, LIU J F, HE J H. Hierarchy of wool fiber and fractal dimension [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2008, 9(3):293-296.

[8] 楊樹, 于偉東, 潘寧. 非織造布的孔洞分形維數對其吸聲性能的影響[J]. 紡織學報, 2010, 31 (12): 28-32. YANG Shu, YU Weidong, PAN Ning. Effect of nonwovens pore fractal dimension on their acoustic absorption behaviors[J]. Journal of Textile Research, 2010, 31(12): 28-32.

[9] SONG W F, YU W D. Heat transfer through fibrous assemblies by fractal method[J]. Journal of Thermal Analysis and Calorimetry, 2012, 110(2): 897-905.

[10] TANG H P, ZHU J L, XI Z P, et al. Impact factors of fractal analysis of porous structure[J]. Science China Technological Sciences, 2010, 53(2): 348-351.

[11] YIN Y, YANG F, LI Y, et al. Fractal geometry and topology abstracted from hair fibers[J]. Applied Mathematics and Mechanics, 2009, 30: 983-990.

[12] 兆禮, 春暉, 曉丹, 等. 現代圖像處理技術及 Matlab 實現[M]. 北京：人民郵電出版社, 2001: 21-23. ZHAO Li, CHUN Hui, XIAO Dan, et al. Modern Image Processing Technology and Matlab Realize[M]. Beijing: Post & Telecom Press,2001: 21-23.

[13] KLEEFELD A, BREUB M, WELK M, et al. Adaptive filters for color images:median filtering and its extensions[C]//[s.n.].International Workshop on Computational Color Imaging.[S.l.]: Springer International Publishing, 2015: 149-158.

[14] CHAKI N, SHAIKH S H, SAEED K. Exploring Image Binarization Techniques[M]. New Delhij: India Springer, 2014: 5-16.

[15] SHOU D, FAN J, DING F. A difference-fractal model for the permeability of fibrous porous media[J]. Physics Letters A, 2010, 374(10): 1201-1204.

[16] MANCUSO S. Fractal geometry-based image analysis of grapevine leaves using the box counting algorithm[J]. VITIS-Journal of Grapevine Research, 2015, 38(3): 97.

Relationship between fractal structure and warmth retention properties of wool fiber assembly

YANG Shu， LI Masha

(NanhuCollege,JiaxingUniversity,Jiaxing,Zhejiang314000,China)

Wool fiber assembly is a porous media whose structure is too complicated to be characterized. To solve this question, the concept of fractal was introduced to fiber assemblies. A box-counting method was used to calculate fractal dimension, and a flat fabric heat retention tester was adopted to test thermal properties of wool fiber assemblies. Then quantitative relation between the fractal dimension and basic structural parameters and thermal properties were acquired. Results indicate the fractal dimension is applicable in characterizing the structure of fiber assemblies, and increases with the increase of the fiber mass and volume fraction, showing more complicated structure. Furthermore, the CLO and warmth retention rate increase with increases of the fractal dimension, while the heat transfer coefficient tends to decrease, i.e. the warmth retention property of fiber assemblies is enhanced.

wool fiber; fiber assembly; box-counting method; fractal dimension; warmth retention property

10.13475/j.fzxb.20160806405

2016-08-27

2017-02-22

國家自然科學基金項目(51403078)；浙江省教育廳科研項目(Y201226223)

楊樹(1985—)，女，講師，博士。主要研究方向為紡織材料。E-mail：yangshu5678@163.com。

TS 102.3

A