基于同余方程和改進的壓扁控制流的混淆算法

王 巖，黃章進，顧乃杰

(1.中國科學技術大學 計算機科學與技術學院，合肥 230027； 2.中國科學技術大學 安徽省計算與通信重點實驗室，合肥 230027； 3.中國科學技術大學 先進技術研究院，合肥 230027)

基于同余方程和改進的壓扁控制流的混淆算法

王 巖1,2,3，黃章進1,2,3*，顧乃杰1,2,3

(1.中國科學技術大學 計算機科學與技術學院，合肥 230027； 2.中國科學技術大學 安徽省計算與通信重點實驗室，合肥 230027； 3.中國科學技術大學 先進技術研究院，合肥 230027)

(*通信作者電子郵箱zhuang@ustc.edu.cn)

針對現有控制流混淆算法的混淆結果單一的問題，提出了一種基于同余方程和改進的壓扁控制流混淆算法。首先，使用密鑰和一組同余方程來生成源代碼的基本塊中需要使用的不透明謂詞；其次，基于Logistic混沌映射提出了一種新的N態不透明謂詞構造算法，并將其應用到現有的壓扁控制流算法中，對現有的壓扁控制流算法進行改進；最后，將上述兩個對源碼進行混淆的算法結合，以此來增加源代碼中控制流的復雜度，使其更難被破解。與現有的基于混沌不透明謂詞的壓扁控制流算法相比，所提混淆算法使混淆后代碼的防篡改攻擊時間平均提高了22%以上，總圈復雜度平均提高了34%以上。實驗結果表明，所提算法能夠保證混淆后程序執行結果的正確性并且具有很高的圈復雜度，能夠有效地抵抗靜態攻擊和動態攻擊。

代碼混淆；N態不透明謂詞；同余方程；壓扁控制流算法

0 引言

近年來隨著軟件技術的飛速發展，軟件代碼的安全保護越來越引起人們的重視。為了提高軟件的可靠性，代碼混淆作為一種抵抗軟件逆向分析的方法被提出[1]。代碼混淆[2]是指對擬發布的應用程序進行保持語義轉換，使得變換后的程序與原來的程序在功能上相同或相近，但更難被理解和反編譯。Collberg等[2-5]將代碼混淆分為外形混淆、數據混淆、預防性混淆和控制混淆四類。控制混淆相對于其他三種混淆具有更好的安全性，是當下代碼混淆領域主要的研究熱點。控制混淆主要依賴于不透明謂詞[3]。Arboit[6]表明可以將謂詞進行參數化來構造更加復雜的謂詞，并提出了一種使用二次剩余構造不透明謂詞的方法。但是，Myles等[7]在其實驗中證明了使用二次剩余構造出的不透明謂詞在安全性方面表現得很差。袁征等[8]提出了一種基于初等數論里面的同余方程來生成不透明謂詞的方法。這種不透明謂詞存在形式過于簡單、安全性差的缺點，在逆向分析過程中較容易被過濾[1]。蘇慶等[1]通過改進Logistic混沌映射，提出了一種新的混沌映射，使用該映射構造出了一種混沌不透明謂詞，但是這種混沌不透明謂詞只有在結果為真時才具有相對較高的密碼安全性。

Wang[9]第一次提出了基于switch-case的控制流壓扁算法。這個算法將源代碼劃分成基本塊，將基本塊打亂后放入switch-case結構中；由case中的條件變量來控制基本塊的執行順序，將其按照源碼中基本塊原來的執行順序來執行；最后將switch封裝到死循環中，當執行完最后一個基本塊時，退出死循環。吳偉民等[10]在此基礎上提出了N態二維混沌不透明謂詞，將二態不透明謂詞擴展成N態；然后將其應用于控制流壓扁算法中的switch-case語句中的case常量表達式中。這在一定程度上提高了逆向分析的難度。但是，給case中控制下一步switch走向的變量賦的是常量值，使其暴露在攻擊者的視野中，在一定程度上降低了破解的難度。

本文利用密鑰和若干同余方程組解的狀態來生成不透明謂詞，并將其應用于源代碼的基本塊中，這種構造方法與陳代梅等[11]提出的使用同余方程和中國剩余定理來構造不透明謂詞的方法相比，省去了對生成的多項式進行兩兩互素的計算，減少了計算時間，且產生的不透明謂詞為True或False的幾率基本相同。本文基于分段Logistic混沌映射[12]提出了一種新的N態混沌不透明謂詞的構造算法，并將其與吳偉民等[10]改進的壓扁控制流算法相結合，隱藏對case語句中控制變量的賦值。依此對源代碼進行控制流混淆，混淆后的代碼不僅具有很高的安全性，并且具有很高的圈復雜度，能夠有效地抵抗逆向工程的攻擊。

1 基本概念

1.1 不透明謂詞

定義1 不透明謂詞[1]。對于一個謂詞P，如果程序中點p的輸出在嵌入程序之前就已知，則該謂詞P是不透明的。如果謂詞P的輸出永遠為真，則記為PT；如果謂詞P的輸出永遠為假，則記為PF；如果謂詞的輸出有時為真有時為假，則記為P?。

定義2 陷門不透明謂詞[1]。令Kj為謂詞P的密鑰，若Kj已知，則混淆前很容易確定謂詞P在程序中點p上的輸出;否則若Kj未知，則混淆前難以確定謂詞P在程序中點p上的輸出，則稱謂詞為陷門不透明謂詞。

定義3N態不透明謂詞[10]。對于某一確定的實現機制，不透明謂詞表達式P=E(O)的可能取值為1,2,…,N，其中O為謂詞定義域，通過表達式映射E所對應的P構成了N態不透明謂詞。

1.2 不透明謂詞的插入

在程序中插入的不透明謂詞主要有永真不透明謂詞、永假不透明謂詞、可真可假的不透明謂詞。在程序中插入不透明謂詞的方法如圖1～3所示[11]，圖中：Bi(i=1,2,3)表示程序中的基本塊，f(Bi)表示基本塊Bi的語義，實線表示可能的執行路徑，虛線表示永遠不會執行的路徑，PT表示不透明謂詞的輸出為True，PF表示不透明謂詞的輸出為False，P?表示不透明謂詞的輸出為True或False，B2bug表示垃圾代碼。不透明謂詞的插入方式就是在基本塊之間添加一個條件判斷語句，根據不透明謂詞輸出的結果判斷執行哪個基本塊。

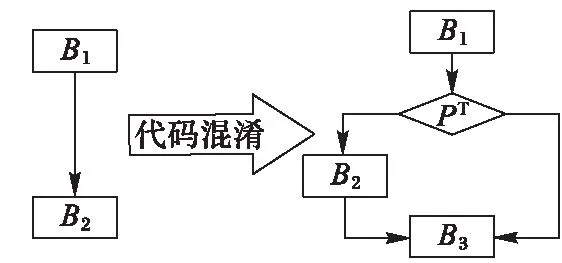
圖1 永真不透明謂詞

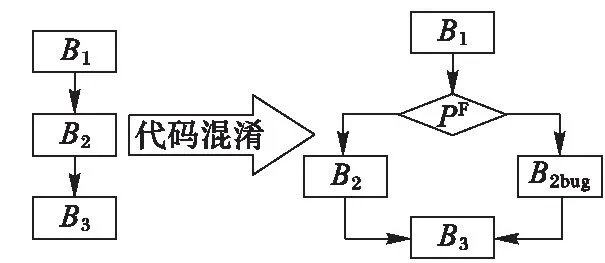
圖2 永假不透明謂詞(f(B2)≠f(B2bug))

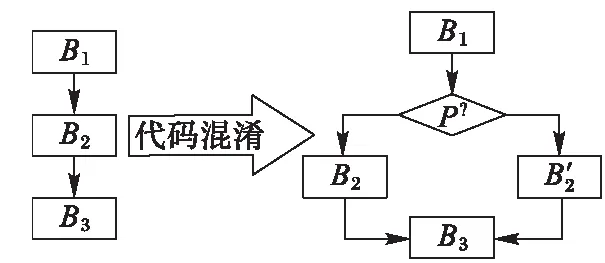
圖3 可真可假不透明謂詞

2 代碼混淆算法

本章首先描述不透明謂詞的構造算法，然后提出基于分段Logistic映射的N態不透明謂詞的構造算法，最后給出改進后的壓扁控制流算法。

2.1 構造不透明謂詞

記模素數p的Legendre符號為(d/p)。

同余方程[13]如下：

1)同余方程1：

x2=-1(modp)

(1)

當-1/p=1，即p=4k+1(k∈Z)時有解，設最小整數解為x1。

2)同余方程2：

x2=2(modp)

(2)

當2/p=1，即p=8k+1或p=8k+7(k∈Z)時有解，設最小整數解為x2。

3)同余方程3：

x2=-2(modp)

(3)

當-2/p=1，即p=8k+1或p=8k+3(k∈Z)時有解，設最小整數解為x3。

4)同余方程4：

x2=3(modp)

(4)

當3/p=1，即p=12k+1或p=12k+11(k∈Z)時有解，設最小整數解為x4。

5)同余方程5：

x2=-3(modp)

(5)

當-3/p=1，即p=6k+1(k∈Z)時有解，設最小整數解為x5。

本文構造不透明謂詞的過程如下：

1)設Nj∈Z+(j=1,2,…,n)，隨機生成Nj個整數(k1,k2,…,kNj)為謂詞Pj的密鑰，對于每個整數ki，根據式(1)～(5)中判定是否有解的等式(如p=4k+1)，將ki代入其中，至少有一個解p是素數。

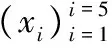
3)對于每個Nj產生的五元組解，將每一組解中互相對應每一位進行異或操作，最后得到一個五元組解記為(r1,r2,…,r5)。

4)根據其中1的個數來判斷不透明謂詞的輸出，當1的個數為奇數時不透明謂詞輸出為True，當1的個數為偶數時不透明謂詞輸出為False。

表1～2給出了本文提出的算法與陳代梅等[11]提出的算法在產生結果為True的不透明謂詞的個數和產生不透明謂詞的時間上的實驗結果對比。

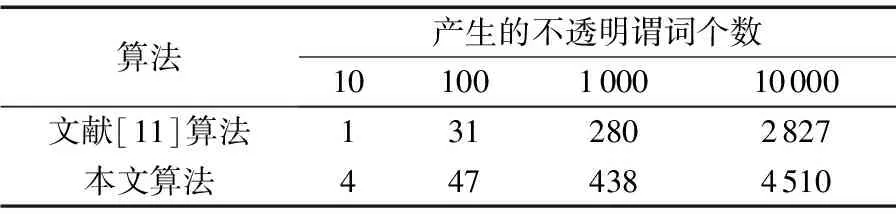
表1 結果為True的不透明謂詞的個數對比

根據表1中的數據，本文提出的算法產生的不透明謂詞結果為True或False的個數基本相同，產生10～10 000個不透明謂詞時，結果為True的混沌不透明謂詞分別占40%、47%、43.8%、45.1%，生成不透明謂詞的個數越多，其百分比越接近50%，結果為True或False的混沌不透明謂詞的個數越接近。本文提出的算法在生成不透明謂詞的均衡性方面優于陳代梅等[11]提出的算法。

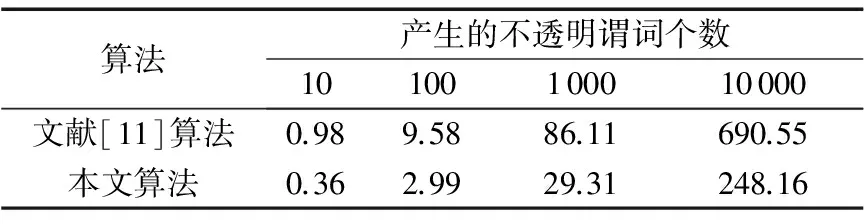
表2 產生不透明謂詞的時間對比 ms

由表2的數據可知，在產生10個～10 000個不透明謂詞時，使用本文提出的算法所消耗的時間相對于陳代梅等[11]提出的算法所消耗的時間分別降低了63.38%、68.79%、65.96%、64.06%，其開銷小于使用陳代梅等[11]的算法產生的開銷。

2.2 基于分段Logistic映射的N態不透明謂詞構造算法

分段Logistic混沌映射[12]具有非線性性質，采用此映射生成混沌序列時不需要進行擾動運算，能夠保證生成的算法具有更好的效率和安全性。定義如下：

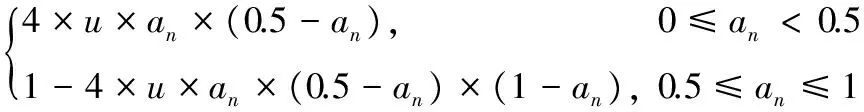
(6)

其中，3.569 946…≤u≤4，a0∈(0,1)。

以下所述N態不透明謂詞構造算法就是定義3中的實現機制E，而密鑰(a0,u,fun)就是其中的謂詞。本文構造N態不透明謂詞的算法描述如下：

步驟1 根據式(6)對參數的要求，使用隨機生成的二元組密鑰(a0,u)進入混沌系統產生隨機實數序列A={a1,a2,…,aN}。

步驟2 通過映射函數fun將實數序列A={a1,a2,…,aN}映射成整數序列F={F1,F2,…,FN}，此時添加映射函數后，密鑰變成三元組：(a0,u,fun)。

步驟3 統計F中出現的不重復元素的個數t(t∈[1,N])，并將其對應的密鑰存放在數組R中。

步驟4 不斷重復步驟1～步驟3，訓練出與不同t值對應的N個密鑰。存放密鑰的數組R={result1,result2,…,resultN}，其中resulti為步驟3中不重復元素個數t等于i時所對應的密鑰(a0i,ui,fun)，以此類推。

假設Fi的取值范圍為[0,m]，步驟2中使用的映射函數fun為：

Fi=Round{ai×m}

(7)

其中Round是取整函數。

2.3 改進的壓扁控制流算法

在吳偉民等[10]提出的控制流壓扁算法中，對控制變量的賦值為暴露在外的常量值，如算法1所示。針對這種情況，本文使用基于分段Logistic混沌映射產生的N態不透明謂詞替換這些常量值，并將2.1節中生成不透明謂詞的算法應用到程序中的基本塊上。改進后的算法如算法2所示。

算法1 文獻[10]提出的控制流壓扁算法。

1)

next=2;

2)

while(next!= 1) {

3)

switch(next) {

4)

caseChaoOpp(ValuesOne):

5)

blockA;

6)

next=3;

7)

break;

8)

caseChaoOpp(ValuesTwo):

9)

blockB;

10)

next=1;

11)

break;

12)

}

13)

}

在算法1中，函數ChaoOpp是吳偉民等[10]提出的N態不透明謂詞的生成方法，ValuesOne和ValuesTwo是其生成不透明謂詞所需的密鑰，blockA、blockB、blockC是程序中的基本塊，在第1)、6)、10)行中，對next變量賦予的常量值直接暴露在外。

算法2 本文提出的改進的控制流壓扁算法。

1)

next=logistic(R1);

2)

while(next!= 1) {

3)

switch(next){

4)

caseChaoOpp(ValuesOne):

5)

if(cPredic(PTrue))

6)

blockA;

7)

next=logistic(R2);

8)

break;

9)

caseChaoOpp(ValuesTwo):

10)

if(cPredic(PFalse)) {

11)

blockBug;}

12)

else{

13)

blockB;

14)

next=logistic(R3);

15)

break;

16)

}

17)

}

18)

}

在算法2中，函數logistic是本文基于分段Logistic映射產生N態不透明謂詞的方法，參數R1～R3是使用2.2節中提出的算法生成的密鑰，函數cPredic是2.1節中提出的生成不透明謂詞的算法，其參數PTrue和PFalse分別是與其對應的生成永真和永假謂詞的密鑰，blockBug為插入的垃圾代碼的基本塊。使用這種算法讓程序的控制流程更加難以被分析，安全性更高。

3 實驗結果與分析

本文提出的算法均使用Python語言實現，并針對幾個開源的Python程序進行性能測試。

3.1 正確性

對源碼進行控制流混淆，首先必須保證其正確性，即混淆后的源碼在功能上與混淆前的源碼一致，并且擁有相同的輸出結果。為了對本文提出的混淆算法進行測試，選了3個開源的Python工具進行測試，結果如表3所示。

表3 混淆前后程序功能對比

從表3中可以看出，混淆前后的輸出結果相同。理論上分析，使用N態不透明謂詞隱藏程序的控制流，并沒有真正改變其基本塊的執行順序，因此并不會影響程序的功能和輸出結果。

3.2 安全性

本文使用同余方程生成的不透明謂詞以及生成的N態不透明謂詞，其結果只有在執行的過程中才能確定，即本文生成的不透明謂詞是陷門不透明謂詞，靜態分析并不能確定其輸出結果，因此本文提出的生成不透明謂詞的算法可以有效地抵抗靜態攻擊。

由于動態攻擊的難點是確定不透明謂詞的輸出[11]。本文對于基本塊中使用的謂詞是通過密鑰和同余方程的解產生，而N態不透明謂詞的生成也是根據三元組或四元組密鑰產生，且密鑰是隨機生成的，同余方程解的狀態也是隨機的，因此可以有效地抵抗動態攻擊。

為了對本文提出的混淆算法進行測試，選了3個開源的Python程序進行防篡改攻擊測試，具體統計結果如表4所示。

由表4中的數據可知， 相比使用文獻[10]算法，使用本文算法Pycrypto-master混淆后產生的攻擊時間增加了28.57%，Docutils增加了29.26%，Jieba-master增加了22.85%。混淆后代碼的攻擊時間相比于混淆前大大增加，并且使用本文算法比使用文獻[10]算法產生的攻擊時間平均高了22%以上，使代碼變得更加難被篡改。

表4 代碼的防篡改攻擊能力對比 h

3.3 開銷

開銷主要表現在時間和空間上。時間方面的開銷主要是判斷不透明謂詞的輸出，空間方面的開銷主要是插入更改控制流的代碼。下面分別對表3中的開源測試案例進行混淆，并對比其混淆前后在時間和空間方面的開銷。

3.3.1 時間開銷

通過對表3中的開源測試用例進行混淆，混淆前后的時間開銷如圖4所示。從圖4中可以看出，混淆后程序的執行時間比混淆前要長。其中：Docutils混淆后較混淆前運行時間增加了8.08%；Pycrypto-master增加了4.04%；Jieba-master增加了3.09%。但隨著程序的不斷增大，增加的時間開銷會不斷變小，卻給程序的破解增加了非常大的難度，因此，這種算法是可取的。

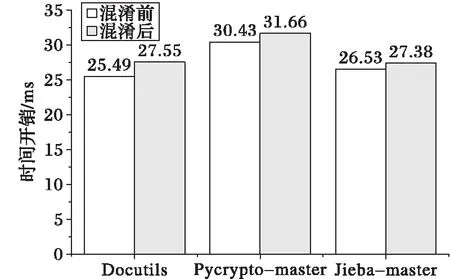
圖4 混淆前后測試用例的時間對比

3.3.2 空間開銷

在空間開銷方面，從圖5中可以看出，混淆后的程序比混淆前的程序占用的空間增加了。其中：Pycrypto-master混淆后較混淆前運行空間增加了10.33%；Docutils增加了9.30%；Jieba-master增加了0.13%。但隨著程序的不斷增大，空間開銷會越來越小，不會對程序造成很大的負擔。

3.4 圈復雜度

現階段并沒有對混淆后程序的復雜度進行評價的統一標準。圈復雜度是衡量一個衡量程序復雜度的度量指標[14]。Radon[15]可以統計Python代碼的總圈復雜度。通過多次實驗，具體統計結果如表5所示。

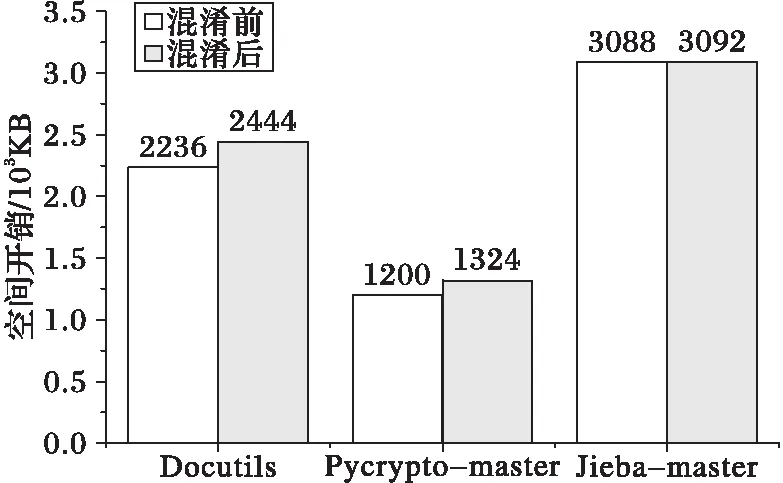
圖5 混淆前后測試用例的空間對比

程序混淆前文獻[10]算法混淆后Pycrypto?master208328173935Docutils569771459616Jieba?master196248337

由表5中的數據可知：Pycrypto-master混淆后較混淆前的總圈復雜度增加了88.91%；Docutils增加了68.79%；Jieba-master增加了71.94%。與使用文獻[10]算法相比，Pycrypto-master混淆后產生的總圈復雜度增加了39.69%；Docutils增加了34.58%；Jieba-master增加了35.89%。混淆后代碼的總圈復雜度相比混淆前大大增加，并且比使用文獻[10]算法產生的總圈復雜度平均提高了34%以上，代碼變得更加復雜。因此，混淆后的代碼更難被破解。

4 結語

本文提出了一種簡單的基于密鑰和同余方程解的狀態的不透明謂詞生成算法，可大量應用于基本塊中。針對當前壓扁控制流算法存在的弊端，提出了一種新的N態不透明謂詞生成算法，并對原有的壓扁控制流算法進行改進。最后在正確性、安全性、開銷、圈復雜度等方面對本文提出的算法進行了評估。實驗結果和分析表明本文提出的算法在正確性和安全性方面表現得很好，具備非常高的圈復雜度，能夠有效地抵抗靜態攻擊和動態攻擊。然而，提高代碼的混淆度的同時，也增加了時間和空間開銷。因此，對于如何在兩者之間取得平衡，還需要進一步的研究。

)

[1] 蘇慶,吳偉民,李忠良，等.混沌不透明謂詞在代碼混淆中的研究與應用[J].計算機科學,2013,40(6):155-159.(SUQ,WUWM,LIZL,etal.Researchandapplicationofchaosopaquepredicateincodeobfuscation[J].ComputerScience, 2013, 40(6): 155-159.)

[2]COLLBERGC,THOMBORSONC,LOWD.Ataxonomyofobfuscatingtransformations,TR#148[R].Auckland,NewZealand:UniversityofAuckland,1997.

[3]COLLBERGC,THOMBORSONC,LOWD.Manufacturingcheap,resilient,andstealthyopaqueconstructs[C] //Proceedingsofthe25thACMSIGLAN-SIGACTSymposiumonPrinciplesofProgrammingLanguages.NewYork:ACM, 1998: 184-196.

[4]COLLBERGC,THOMBORSONC,LOWD.Breakingabstractionsandun-structuringdatastructures[C] //ICCL’98:Proceedingsof1998InternationalConferenceonComputerLanguages.Piscataway,NJ:IEEE, 1998: 28-38.

[5]COLLBERGCS,THOMBORSONCD,LOWDWK.Obfuscationtechniquesforenhancingsoftwaresecurity:US, 6668325 [P]. 2003- 12- 23.

[6]ARBOITG.AmethodforwatermarkingJavaprogramsviaopaquepredicates[C/OL] //Proceedingsofthe2002InternationalConferenceonElectronicCommerceResearch. [2016- 10- 16].http://profs.scienze.univr.it/～giaco/download/Watermarking-Obfuscation/sp-paper.pdf.

[7]MYLESG,COLLBERGC.Softwarewatermarkingviaopaquepredicates:implementation,analysis,andattacks[J].ElectronicCommerceResearch, 2006, 6(2): 155-171.

[8] 袁征,馮雁,溫巧燕,等.構造一種新的混淆Java程序的不透明謂詞[J].北京郵電大學學報,2007,30(6):103-106.(YUANZ,FENGY,WENQY,etal.ManufactureofanewopaquepredicateforJavaprograms[J].JournalofBeijingUniversityofPostsandTelecommunications, 2007, 30(6): 103-106.)

[9]WANGCX.Asecurityarchitectureforsurvivabilitymechanisms[D].Charlottesville,VA:UniversityofVirginia, 2001: 65-68.

[10] 吳偉民,林水明,林志毅.一種基于混沌不透明謂詞的壓扁控制流算法[J].計算機科學,2015,42(5):178-182.(WUWM,LINSM,LINZY.Chaotic-basedopaquepredicatecontrolflowflattenalgorithm[J].ComputerScience, 2015, 42(5): 178-182.)

[11] 陳代梅,范希輝,朱靜,等.基于同余方程和中國剩余定理的混淆算法[J].計算機應用研究,2015,32(2):485-488.(CHENDM,FANXH,ZHUJ,etal.ObfuscationalgorithmsbasedoncongruenceequationandChineseremaindertheorem[J].ApplicationResearchofComputers, 2015, 32(2): 485-488.)

[12] 王興元,朱偉勇.二維Logistic映射中混沌與分形的研究[J].中國圖象圖形學報,1999,4(4):340-344.(WANGXY,ZHUWY.ResearchesonchaosandfractalofthecoupledLogisticmap[J].JournalofImageandGraphics,1999, 4(4): 340-344.)

[13] 潘承洞,潘承彪.簡明數論[M].北京:北京大學出版社,1998:150-162.(PANCD,PANCB.SimplifiedNumberTheory[M].Beijing:PekingUniversityPress, 1998: 150-162.)

[14] 趙玉潔,湯戰勇,王妮,等.代碼混淆算法有效性評估[J].軟件學報,2012,23(3):700-711.(ZHAOYJ,TANGZY,WANGN,etal.Evaluationofcodeobfuscatingtransformation[J].JournalofSoftware, 2012, 23(3): 700-711.)

[15]LACCHIAM.Radon:acodemetricstoolinPython[EB/OL]. [2016- 10- 16].https://pypi.python.org/pypi/radon.

ThisworkispartiallysupportedbytheAnhuiProvincialNaturalScienceFoundation(1408085MKL06),theProgramforInnovationoftheDisciplineHigherEducation(B07033).

WANG Yan, born in 1991, M.S. candidate. His research interests include software technology, program optimization.

HUANG Zhangjin, born in 1980, Ph. D., associate professor. His research interests include computer graphics, graphic processing unit computation.

GU Naijie, born in 1961, M. S., professor. His research interests include parallel algorithm, parallel processing, parallel architecture.

Obfuscating algorithm based on congruence equation and improved flat control flow

WANG Yan1,2,3, HUANG Zhangjin1,2,3*, GU Naijie1,2,3

(1.SchoolofComputerScienceandTechnology,UniversityofScienceandTechnologyofChina,HefeiAnhui230027,China; 2.AnhuiProvinceKeyLaboratoryofComputingandCommunicationSoftware,UniversityofScienceandTechnologyofChina,HefeiAnhui230027,China; 3.InstituteofAdvancedTechnology,UniversityofScienceandTechnologyofChina,HefeiAnhui230027,China)

Aiming at the simple obfuscating result of the existing control flow obfuscating algorithm, an obfuscating algorithm based on congruence equation and improved flat control flow was presented. First of all, a kind of opaque predicate used in the basic block of the source code was created by using secret keys and a group of congruence equation. Then, a new algorithm for creatingN-state opaque predicate was presented based on Logistic chaotic mapping. The proposed algorithm was applied to the existing flat control flow algorithm for improving it. Finally, according to the combination of the above two proposed algorithms for obfuscating the source code, the complexity of the flat control flow in the code was increased and make it more difficult to be cracked. Compared with the flat control flow algorithm based on chaotic opaque predicate, the code’s tamper-proof attack time of the obfuscated code was increased by above 22% on average and its code’s total cyclomatic complexity was improved by above 34% on average by using the proposed obfuscating algorithm. The experimental results show that, the proposed algorithm can guarantee the correctness of execution result of the obfuscated program and has a high cyclomatic complexity, so it can effectively resist static and dynamic attacks.

code obfuscation;N-State opaque predicate; congruence equation; flat control flow algorithm

2016- 11- 15;

2016- 12- 21。

安徽省自然科學基金資助項目(1408085MKL06)；高等學校學科創新引智計劃項目(B07033)。

王巖(1991—)，男，山東濟南人，碩士研究生，CCF會員，主要研究方向：軟件技術、程序優化； 黃章進(1980—)，男，湖北天門人，副教授，博士，CCF會員，主要研究方向：計算機圖形學、圖形處理器計算； 顧乃杰(1961—)，男，江蘇南通人，教授，碩士，CCF會員，主要研究方向：并行算法、并行處理、并行體系機構。

1001- 9081(2017)06- 1803- 05

10.11772/j.issn.1001- 9081.2017.06.1803

TP311.56

A