Zodiac密碼算法的多維零相關線性分析

程 璐，魏悅川，潘曉中，李安輝

(1.武警工程大學 電子技術系,西安 710086; 2.網絡與信息安全武警部隊重點實驗室,西安 710086)

Zodiac密碼算法的多維零相關線性分析

程 璐1,2*，魏悅川1,2，潘曉中1,2，李安輝1,2

(1.武警工程大學 電子技術系,西安 710086; 2.網絡與信息安全武警部隊重點實驗室,西安 710086)

(*通信作者電子郵箱18302972151@163.com)

分組密碼算法Zodiac支持3種密鑰長度，分別為Zodiac-128、Zodiac-192、Zodiac-256。利用零相關線性分析方法評估了Zodiac算法的安全性，首先根據算法的結構特性，構造了一些關于Zodiac算法的10輪零相關線性逼近，然后對16輪Zodiac-192進行了多維零相關分析。分析結果顯示：攻擊過程中一共恢復了19個字節的密鑰，其數據復雜度約為2124.40個明密文對，計算復雜度為2181.58次16輪加密。由此可得：16輪(即全輪)192 bit密鑰的Zodiac算法(Zodiac-192)對于零相關線性分析方法是不安全的。

分組密碼；Zodiac密碼算法；線性掩碼；線性逼近；零相關線性分析

0 引言

Zodiac是分組密碼算法的代表之一，由韓國專家Lee等[1]于2000年為韓國公司SoftForum所設計。Zodiac算法是典型的Feistel結構，共有16輪迭代。其明文分組長度為128 bit，密鑰長度有三種128 bit、192 bit、256 bit，分別可記作Zodiac-128、Zodiac-192、Zodiac-256[12]。目前針對Zodiac的分析有不可能差分分析、積分分析和中間相遇分析等。

目前對Zodiac最好的分析結果是不可能差分分析， Shakiba等[2]利用2個13輪的不可能差分，攻擊全輪Zodiac算法，時間復雜度為271.3次全輪加密，數據復雜度為271.28個選擇明文；張鵬等[3]利用Zodiac的等價結構找到了兩個新的9輪Square區分器，利用新的區分器攻擊了全輪Zodiac，其時間復雜度為2189.5次全輪加密，數據復雜度為212.6個選擇明文；孫兵等[4]構造了一個16輪的不可能差分以及一個9輪的積分區分器，并在此區分器前面增加1輪，后面增加6輪，實現對全輪Zodiac算法的積分攻擊，其時間復雜度為2190次全輪加密，數據復雜度為216個選擇明文；海昕等[5]利用中間相遇攻擊分析Zodiac算法，找到了一個10輪的區分器，對全輪Zodiac算法進行了攻擊，其時間復雜度為2105.3次全輪加密，數據復雜度為228.9個選擇明文，其預計算所需要的時間復雜度為2121.9次全輪加密。

由前面的描述可以看出，為評估Zodiac算法的安全性，研究者們已經做了很多工作。然而，Zodiac對于零相關線性分析的結果還是空白。零相關線性分析方法由Bogdanov等[6]在2012年第一次提出，其最大缺陷是攻擊所需數據復雜度較高。為了進一步降低數據復雜度，Bogdanov等[7]于FSE2012(International Conference on Fast Software Encryption)提出利用多條零相關線性逼近區分統計分布的理論模型，即多重零相關線性分析，但是要求多條零相關線性逼近相互獨立，此假設是很難滿足的。Bogdanov等[8]于ASIACRYPT2012提出多維零相關線性分析的模型，克服了多重零相關線性分析所要求的強假設條件，所需數據量和多重零相關基本相當，進一步完善了零相關線性分析模型。零相關線性分析模型的有效性，在對AES[6]、LBlock[9]、TWINE[9]、E2[10]、SMS4[11]、FOX[12]及MIBS[13]等一系列重要密碼算法的分析中得到了驗證，因此利用零相關線性分析來評估部分分組密碼算法的安全性，是當前分組密碼分析的一個熱點。

本文首次利用零相關線性分析方法分析Zodiac密碼算法。根據Zodiac算法結構特性，構造了10輪零相關線性逼近，之后對16輪(全輪)的Zodiac-192進行了多維零相關線性分析。整個攻擊過程共恢復了19個字節的密鑰，由此可得全輪Zodiac-192對于零相關線性分析方法是不安全的，而且其分析結果相比其他研究用不同方法進行攻擊的部分結果有一定的優化。

1 預備知識

1.1 符號說明

1.2Zodiac算法簡介

Zodiac算法的主體結構采用Feistel結構，共16輪迭代。在第一輪迭代之前有一個初始置換T*，在最后一輪迭代之后有一個末置換T*，并且在迭代前后分別異或于一個白化密鑰，如圖1所示，其中：K0、K17為64 bit的白化密鑰，Ki(1≤i≤16)為第i輪的輪密鑰，F為輪函數。本文的分析中不考慮前后兩個置換，所以不作詳細介紹。

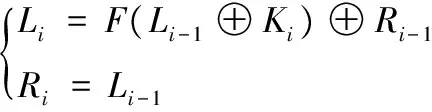
第16輪變換與之前不同，定義為：

密文為：

C=T(L16,R16)

每一輪變換分別由密鑰加K、線性變換P、非線性變換S構成。輪函數的定義為：F(X)=S(P(X))，其中X為64 bit，可按字節表示為X=(x0,x1,x2,x3,x4,x5,x6,x7)，P為線性變換，它將X=(x0,x1,x2,x3,x4,x5,x6,x7)變換為Y=(y0,y1,y2,y3,y4,y5,y6,y7)：y0=x2⊕x3⊕x4，y1=x0⊕x1，y2=x1⊕x2，y3=x2⊕x3，y4=x0⊕x6⊕x7，y5=x4⊕x5，y6=x5⊕x6，y7=x6⊕x7。

由于本文分析中沒有考慮主密鑰與輪子密鑰以及輪子密鑰之間的聯系，所以Zodiac算法的密鑰擴展算法在此不作介紹，具體可參見文獻[1]。

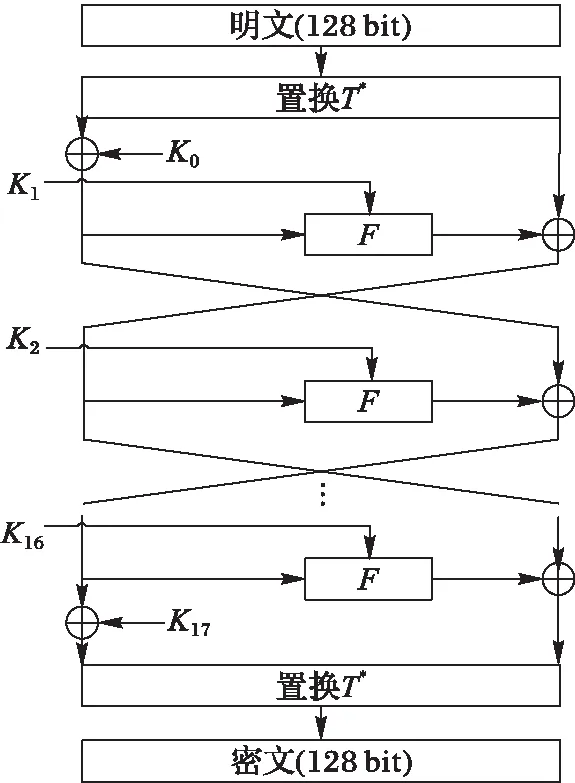
圖1 Zodiac算法的加密結構

1.3 多維零相關線性分析方法

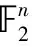
Cf(α,β)=Corx(β·f(x)⊕α·x)= 2Prx(β·f(x)⊕α·x=0)-1

若Cf(α,β)=0，則稱該線性逼近是零相關線性逼近。

多維零相關線性分析[8]方法選取l=2m個零相關線性逼近，并且這些線性逼近由m條相互獨立的線性逼近通過線性關系擴展。不妨記作為(ai→bi)i=0,1,…，m-1。攻擊者選擇N對明密文對，并建立計數器N[z]，其中z是mbit長的字符串。通過在線性逼近前后加輪，窮舉部分子密鑰并部分加解密所選取的明密文對，得到線性掩碼首尾對應的中間狀態，為了方便記作(p′,c′)[12]。然后，對于選擇的每一個明密文對經過部分加解密得到(p′,c′)，通過式(1)得到z的值：

z=(z[0],z[1],…，z[m-1])=(a0·p′⊕b0·c′,a1·p′⊕b1·c′，…，am-1·p′⊕bm-1·c′)

(1)

更新相應的計數器N[z]。然后，計算統計量T：

(2)

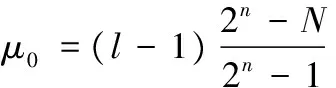
(3)

其中：n是分組長度；z1-α、z1-β為標準正態分布的分位數。對此方法更完整詳細的描述請參考文獻[8]。

2 Zodiac算法10輪零相關線性逼近

本文主要通過以下的方式來構造零相關線性逼近：在相關系數非零條件下線性掩碼從前和從后兩個方向向中間傳播，最后在中間某個位置相遇，并且產生相關系數為零的矛盾狀態。在非零相關系數條件下線性掩碼在分組密碼各組件中有如下傳播規律。

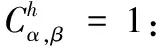
根據命題1，能夠推導出在非零相關系數條件下線性掩碼在分組密碼各組件中的傳播規律。

引理1[14]異或運算。如果h(x1,x2)=x1⊕x2，那么C(β°h(x1,x2),α1°x1⊕α2°x2)≠0，當且僅當β=α1=α2。

引理2[14]分支操作。如果h(x)=(x,x)，那么C((β1,β2)°h(x),α°x)≠0，當且僅當α=β1⊕β2。

引理3[14]可逆F操作。如果φ(x)為可逆函數，則C(β°φ(x),α°x)≠0，當且僅當α與β均為零或者均不為零。

利用這些規律，可以得到Zodiac的10輪零相關線性逼近。

設a和h分別是8 bit長的非零字符串，則(000a000000000000)→(00000000000000h0)是r輪到r+9輪的10輪零相關線性逼近。

證明 如圖2所示，圖中設定“0”表示零掩碼；b、ci、di、ei、f、gi、li(0≤i≤7)表示非零掩碼；“?”表示不確定是零或非零的掩碼。從加密方向，若第r輪的輸入掩碼為(000a000000000000)，向加密方向經過5輪迭代，在非零相關系數條件下第r+4輪左側輸出掩碼為(0c2(c2⊕c3)(c3⊕a)0000)⊕(????e0000)，則其第8個字節為0掩碼；若第r+9輪的輸出掩碼為(00000000000000h0)，向解密方向經過5輪迭代，在非零相關系數條件下第r+5輪右側輸入掩碼為l4000??(l4⊕l6⊕f)l4，則其第8個字節為非0掩碼，與第r+4輪的狀態相矛盾。

證畢。

3 16輪Zodiac-192的多維零相關分析

本章主要利用圖2中構造的10輪(第4輪～第13輪)零相關線性逼近，并且往前擴展3輪往后擴展3輪，對16輪Zodiac-192作多維零相關線性分析，分析過程中不考慮初始置換和末置換以及白化密鑰的影響，如圖3所示。在圖3中，部分加解密所涉及到的狀態字節用“*”標記，其他無關字節則用來“0”標記。Lout、Rout分別表示異或白化密鑰K17之前第16輪左側的64bit輸出及右側64bit輸出。

3.1 攻擊過程

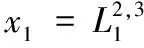
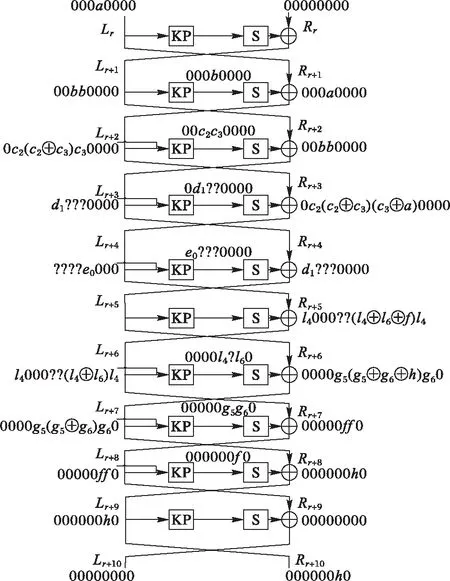
圖2 Zodiac的10輪零相關線性逼近

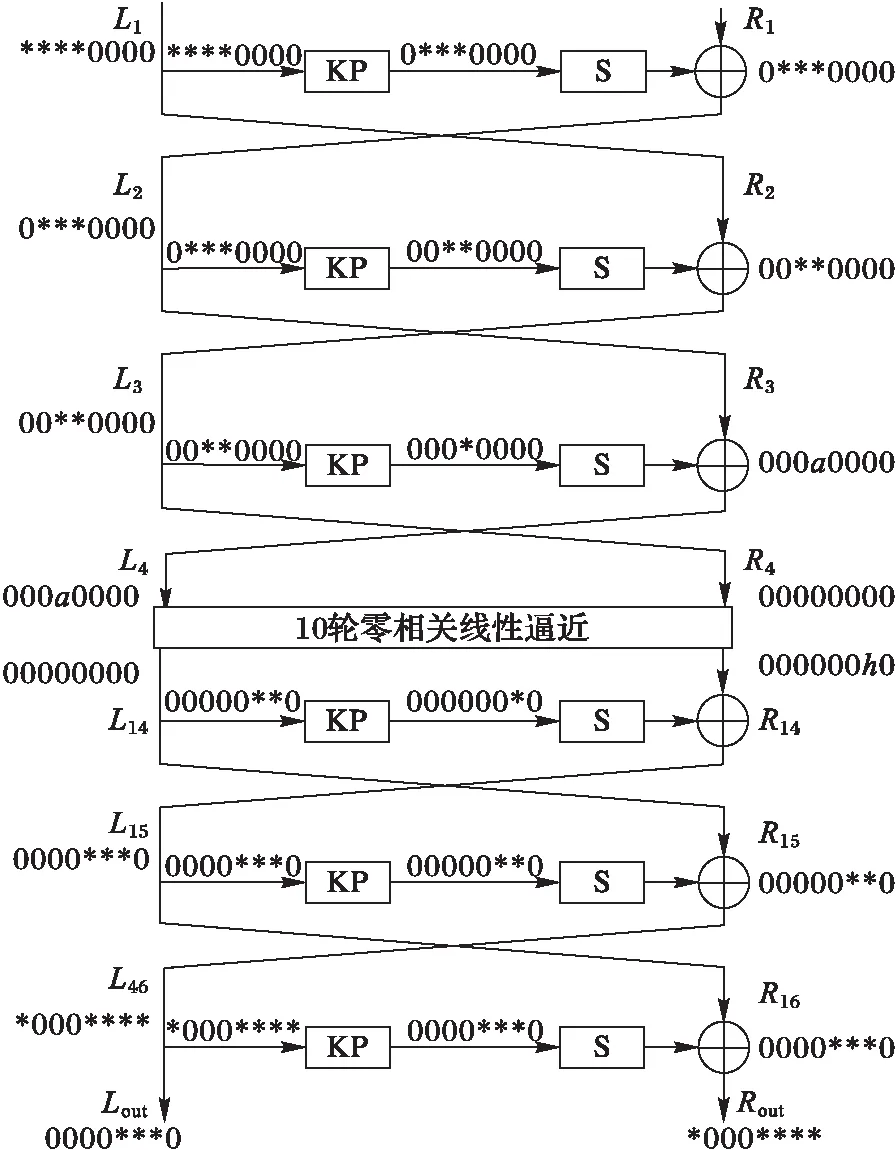
圖3 Zodiac的16輪零相關線性分析

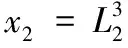
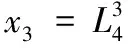
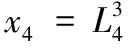
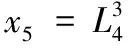
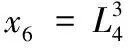
8)z是16 bit字符串，為每一個可能的z建立一個24 bit計數器N[z]，且全部初始化為零。對于16個長度為16 bit的zi(第i+1個比特為1、其他比特為0)。計算z[i]=zi·x6(0≤i≤15)，并且計算z，然后累加計數器N[z]+=N6[x6]。根據式(2)，計算統計量T。

9)如果T≤τ，則所猜測的輪子密鑰可能為正確密鑰，窮盡搜索所有可能的正確密鑰。

3.2 攻擊復雜度

在攻擊過程中，一共恢復了19個字節的密鑰，設α=2-2.7，β=2-152，則z1-α≈1，z1-β≈13.9。又因為n=128，l=216，則由式(3)可得大體需要2124.40個明密文對。判斷的臨界值為τ≈215.89。在本文中，假設訪問一次內存的代價大約是一輪Zodiac-192加密，由于步驟5)～7)的復雜度占計算復雜度的主要部分，而它們的復雜度之和不超過2184×3×1/16≈2181.58次16輪加密。存儲復雜度計算主要集中于步驟1)，大約需要2121.58個字節。所以完成全輪的Zodiac-192攻擊需要得到數據復雜度為2124.40，計算復雜度為2181.58，沒有預計算復雜度。本文方法與其他攻擊方法的復雜度對比如表1所示。由表1的對比結果可知，目前對Zodiac算法最好的攻擊結果是不可能差分攻擊，而本文的零相關線性分析與Square攻擊和積分攻擊相比，在時間復雜度上有明顯優化，與中間相遇攻擊相比，該方法不需要預計算復雜度。

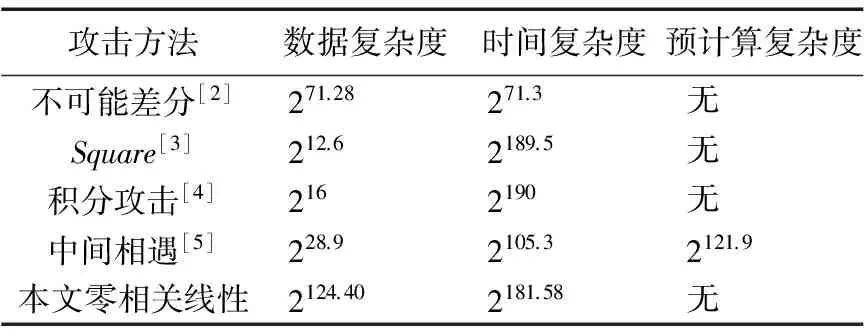
表1 不同攻擊方法的復雜度對比

4 結語

本文主要評估了Zodiac密碼算法關于多維零相關線性分析方法的安全性。首先利用Zodiac算法結構特點，構造了10輪零相關線性逼近，然后對16輪(全輪)的Zodiac-192進行了多維零相關線性分析。整個攻擊過程中共恢復了19個字節的密鑰，所以，16輪Zodiac-192對多維零相關線性分析是不安全的。通過與其他攻擊方法對比可以得出，本文方法在時間復雜度方面優于Square攻擊和積分攻擊，與中間相遇攻擊比較，本文方法沒有預計算復雜度。但本文方法的數據復雜度明顯高于其他方法，進一步研究將考慮通過分析算法的結構特點、密鑰擴展算法等來降低其數據復雜度。

)

[1]LEEC,JUNK,JUNGM,etal.Zodiacversion1.0 (revised)architectureandspecificationStandardizationWorkshoponInformationSecurityTechnology,KoreanContributiononMP18033,ISO/IECJTC1/SC27N2563, 2000[EB/OL]. [2016- 11- 20].http://www.kisa.or.kr/seed/index.html.

[2]SHAKIBAM,DAKHILALIANM,MALAH.AnimprovedimpossibledifferentialcryptanalysisofZodiac[J].JournalofSystemsandSoftware, 2010, 83(4): 702-709.

[3] 張鵬，李瑞林，李超.Zodiac算法新的Square攻擊[J].電子與信息學報,2010,32(11):2790-2794.(ZHANGP,LIRL,LIC.NewsquareattackonZodiac[J].JournalofElectronics&InformationTechnology, 2010, 32(11): 2790-2794.)

[4] 孫兵，張鵬，李超.Zodiac算法的不可能差分和積分攻擊[J].軟件學報，2011,22(8):1911-1917.(SUNB,ZHANGP,LIC.ImpossibledifferentialandintegralcryptanalysisofZodiac[J].JournalofSoftware, 2011, 22(8): 1911-1917.)

[5] 海昕,唐學海,李超.對Zodiac算法的中間相遇攻擊[J].電子與信息學報,2012,34(9):2259-2262.(HAIX,TANGXH,LIC.Themeet-in-the-middleattacksonZodiac[J].JournalofElectronics&InformationTechnology, 2012, 34(9): 2259-2262.)

[6]BOGDANOVA,RIJMENV.Linearhullswithcorrelationzeroandlinearcryptanalysisofblockciphers[J].Designs,CodesandCryptography, 2014, 70(3): 369-383.

[7]BOGDANOVA,WANGMQ.Zerocorrelationlinearcryptanalysiswithreduceddatacomplexity[C]//FSE’12:Proceedingsofthe19thinternationalconferenceonFastSoftwareEncryption.Berlin:Springer, 2012: 29-48.

[8]BOGDANOVA,LEANDERG,NYBERGK,etal.Integralandmultidimensionallineardistinguisherswithcorrelationzero[C]//ASIACRYPT’12:Proceedingsofthe18thInternationalConferenceontheTheoryandApplicationofCryptologyandInformationSecurity.Berlin:Springer, 2012: 244-261.

[9] WANG Y F, WU W L. Improved multidimensional zero-correlation linear cryptanalysis and applications to LBlock and TWINE [C]// ACISP 2014: Proceedings of the 19th Australasian Conference on Information Security and Privacy, LNCS 8544. Berlin: Springer: 2014: 1-16.

[10] WEN L, WANG M Q, BOGDANOV A. Multidimensional zero-correlation linear cryptanalysis of E2 [C]// AFRICACRYPT 2014: Proceedings of the 7th International Conference on Cryptology in Africa, LNCS 8469. Berlin: Springer, 2014: 147-164.

[11] 馬猛,趙亞群,劉慶聰,等.SMS4算法的多維零相關線性分析[J].密碼學報，2015,2(5)：458-466.(MA M, ZHAO Y Q, LIU Q C, et al. Multidimensional zero-correlation linear cryptanalysis on SMS4 algorithm [J]. Journal of Cryptologic Research, 2015, 2(5): 458-466.)

[12] 伊文壇,陳少真.FOX密碼的多維零相關線性分析[J].密碼學報，2015,2(1):27-39.(YI W T, CHEN S Z. Multidimensional zero-correlation linear attacks on FOX block cipher [J]. Journal of Cryptologic Research, 2015, 2(1): 27-39.)

[13] 伊文壇,魯林真,陳少真.輕量級密碼算法 MIBS 的零相關和積分分析[J].電子與信息學報,2016,38(4):819-826.(YI W T, LU L Z, CHEN S Z. Integral and zero-correlation linear cryptanalysis of lightweight block cipher MIBS [J]. Journal of Electronics & Information Technology, 2016, 38(4): 819-826.)

[14] 王美琴,溫隆.零相關線性分析研究[J].密碼學報,2014,1(3):296-310.(WANG M Q, WEN L. Research on zero-correlation linear cryptanalysis [J]. Journal of Cryptologic Research, 2014, 1(3): 296-310.)

This work is partially supported by the National Natural Science Foundation of China (61202492，61572521), the Foundation of Science and Technology on Information Assurance Laboratory (KJ- 15- 010), the Natural Science Foundation of Shaanxi Province (2016JQ6030).

CHENG Lu, born in 1992, M. S. candidate. His research interests include information security, cryptology.

WEI Yuechuan, born in 1982, Ph. D., associate professor. Her research interests include cryptology.

PAN Xiaozhong, born in 1964, M. S., professor. His research interests include information security.

LI Anhui, born in 1993, M. S. candidate. His research interests include information security, complex network.

Multidimensional zero-correlation linear cryptanalysis on Zodiac cipher algorithm

CHENG Lu1,2*, WEI Yuechuan1,2, PAN Xiaozhong1,2, LI Anhui1,2

(1.DepartmentofElectronicTechnology,EngineeringCollegeoftheArmedPoliceForce,Xi’anShaanxi710086,China； 2.KeyLaboratoryofNetwork&InformationSecurityundertheChineseArmedPoliceForce,Xi’anShaanxi710086,China)

Zodiac is a block cipher algorithm and it supports 3 master key lengths which are called Zodiac-128, Zodiac-192 and Zodiac-256. The security of Zodiac algorithm was evaluated by using zero-correlation linear cryptanalysis. Firstly, 10-round zero-correlation linear approximations of Zodiac algorithm were constructed according to the structural characteristics of the algorithm. Then, the multidimensional zero-correlation linear cryptanalysis on 16-round Zodiac-192 was conducted. The analysis results show that 19-byte keys were restored totally in the process of attack, the data complexity was about 2124.40known ciphertexts and the computational complexity was 2181.58encryptions of 16-round. Thus the Zodiac-192 algorithm with the 192-bit key of 16 rounds (full rounds) is not immune to the zero-correlation linear cryptanalysis.

block cipher; Zodiac cipher algorithm; linear mask; linear approximation; zero-correlation linear cryptanalysis

2016- 12- 12;

2017- 02- 26。 基金項目:國家自然科學基金資助項目(61202492，61572521)；信息保障技術國家重點實驗室開放基金(KJ- 15- 010)；陜西省自然科學基金資助項目(2016JQ6030)。

程璐(1992—)，男，河北衡水人，碩士研究生，主要研究方向：信息安全、密碼學； 魏悅川(1982—)，女，天津人，副教授，博士，主要研究方向：密碼學； 潘曉中(1964—)，男，陜西西安人，教授，碩士，主要研究方向：信息安全； 李安輝(1993—)，男，湖南常德人，碩士研究生，主要研究方向：信息安全、復雜網絡。

1001- 9081(2017)06- 1605- 04

10.11772/j.issn.1001- 9081.2017.06.1605

TP309.2

A