基于最優控制的航天器斷續姿控系統設計方法

王 勇，李延軍，張 亮，陳 陽，檀朋碩

基于最優控制的航天器斷續姿控系統設計方法

王 勇，李延軍，張 亮，陳 陽，檀朋碩

（北京宇航系統工程研究所，北京，100076）

傳統基于姿控噴管的斷續姿控系統多采用經典的斜線開關線設計非線性控制律，系統設計時往往難以同時滿足姿控精度、推進劑消耗、噴管開關次數等要求和約束。為進一步優化系統設計，實現各性能指標閉合，提出了基于最優控制的斷續姿控系統二次型開關線控制方法，并推導得到了系統姿控精度模型。通過仿真試驗對比了傳統斜線開關和二次型開關控制的性能。仿真結果表明，兩種方法下系統姿控精度計算模型正確，性能指標各有優劣，姿控系統設計時可依據系統約束綜合考慮選取不同方案。

非線性控制；最優控制；斜線開關；二次型開關

0 引 言

為節省推進劑，在航天器彈道設計時，往往增加一、二次無動力或小動力飛行段，即滑行段。此外，航天器在主動段飛行結束后，往往增加末助推級，以滿足末速修正、載荷釋放調姿等需要。在滑行段和末修級飛行段，由于航天器只受到較小的干擾作用，綜合系統復雜度、質量和能源等方面考慮，往往采用基于姿控噴管的斷續姿控方案[1]。

傳統斷續姿控系統設計時，往往采用經典的斜線開關線設計非線性控制律。該方法較為成熟，但系統設計時往往難以同時滿足姿控精度、推進劑消耗、噴管開關次數等要求和約束[2]。實際上，航天器飛行不同階段時，姿控精度、調姿速度、推進劑消耗等要求和約束存在差異，姿控系統設計時存在進一步優化的空間。隨著控制技術的發展，最優控制等現代控制方法逐漸應用于航天器控制系統設計中[3～6]，為航天器斷續姿控系統設計提供了更多選擇。

本文以三通道解耦后單通道姿控系統設計為例，提出了基于最優控制的斷續姿控系統二次型開關控制方法，并推導得到了系統姿控精度模型。開展了兩種控制方法下的仿真試驗，試驗結果表明，兩種方案下系統姿控精度計算模型正確，性能指標各有優劣，系統設計時可依據不同飛行階段性能指標要求等綜合考慮選取不同方案。

1 航天器姿態控制系統模型

假定航天器三通道已實現解耦控制，以俯仰通道為例，姿態控制系統原理如圖1所示。其中，彈上計算機依據敏感裝置測量得到姿態角和角速度，進行控制指令解算，解耦后通過開關放大器推動電磁閥，控制姿控噴管的開閉，實現姿態的穩定和控制。

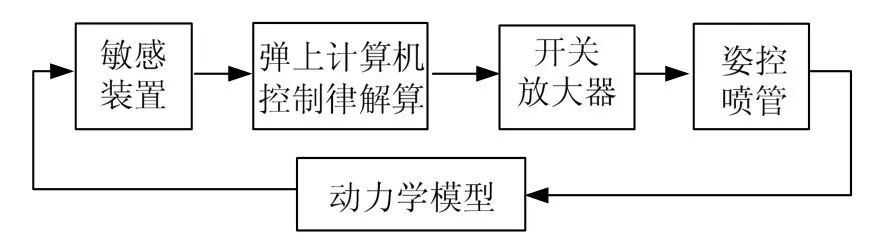
圖1 俯仰通道姿態控制系統原理

1.1 剛體動力學模型

以在真空環境下工作的航天器為例，其俯仰通道剛體動力學模型如下[7]：

式中 Δ?˙為俯仰姿態角加速度；Mz為俯仰通道量化合成干擾力矩，Mz=Mz/Jz，Mz為俯仰通道干擾力矩，Jz為對應的轉動慣量；b3為俯仰通道控制力矩系數；K?為姿控噴管的3個狀態，K?=1，0，-1，分別表示修正正向姿態偏差的噴管開啟、關閉和修正負向姿態偏差的噴管開啟。

1.2 開關放大器特性

開關放大器一般具有滯環的繼電特性，為實現斷續控制往往設置死區，其特性如圖2所示[8]。

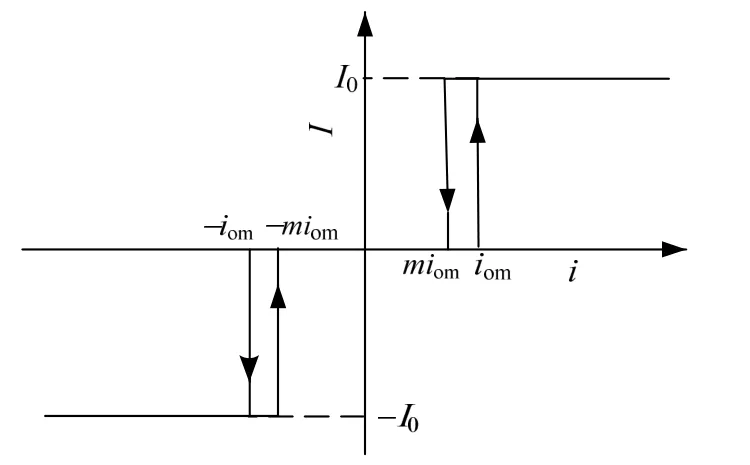
圖2 帶滯環的開關非線性特性

姿控噴管控制信號k?取值計算如下：

2 斜線開關控制方法

式中 ?Δ為姿態角偏差；?Δ˙為姿態角速度偏差；b為系統動態增益。

此時，在不考慮延遲情況下：

噴管正向理論開關線為

傳統斷續姿控系統設計時，姿控噴管開關控制切換線設計為斜線開關，其校正網絡傳遞函數為一階微分形式，即取：

噴管負向理論開關線為

斜線開關控制時，姿控系統進入穩定后，系統相軌跡無法收斂于零點，而是形成一個穩定的極限環[2]。系統進入極限環狀態后，姿態角偏差Δ?和姿態角速度偏差Δ?˙的最大值稱為極限環參數，分別用Δ?T和Δ?˙T表示。當Mz＞0時，斜線開關控制律下系統姿控精度為

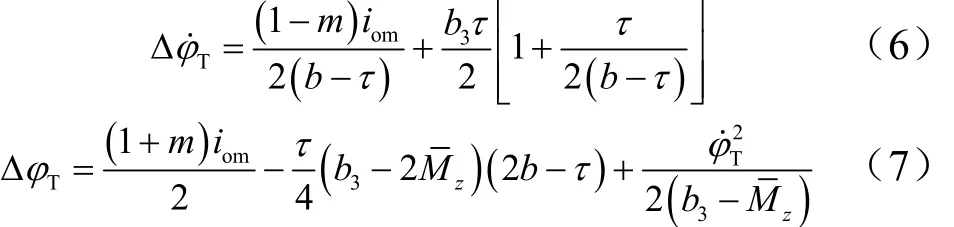
式中 τ為系統時延，包括開關放大器、姿控噴管以及采用數控方案時的計算與采樣時延，本文假定系統開啟與關閉時延均為τ。

3 基于最優控制的二次型開關控制方法

3.1 二次型開關控制律設計

采用最優控制理論設計斷續姿態控制系統控制律。以俯仰通道為例，狀態方程為

式中 x=[?, ?˙]T；x0為系統初始狀態；u為開關控制量，只有3個值1，0和-1；A為系數矩陣；B為控制矩陣，且

采用時間最優控制時，系統的性能指標J為

應用極小值原理，取系統哈密爾頓函數H為

解式（13）得：

由極小值原理可以得：

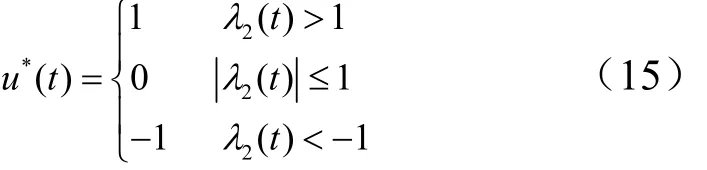
經推導，綜合考慮開關放大器工作特性，得到二次型開關控制律，開關曲線方程為

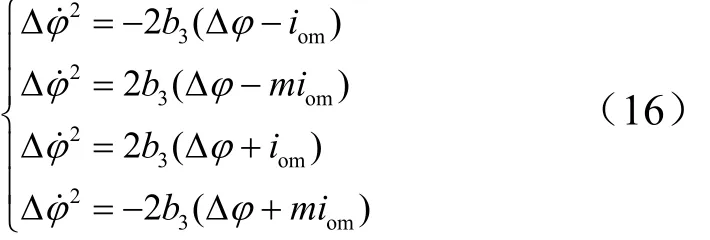
3.2 控制精度分析

考慮開關放大器滯環特性的二次型開關控制相平面極限環曲線如圖3所示。

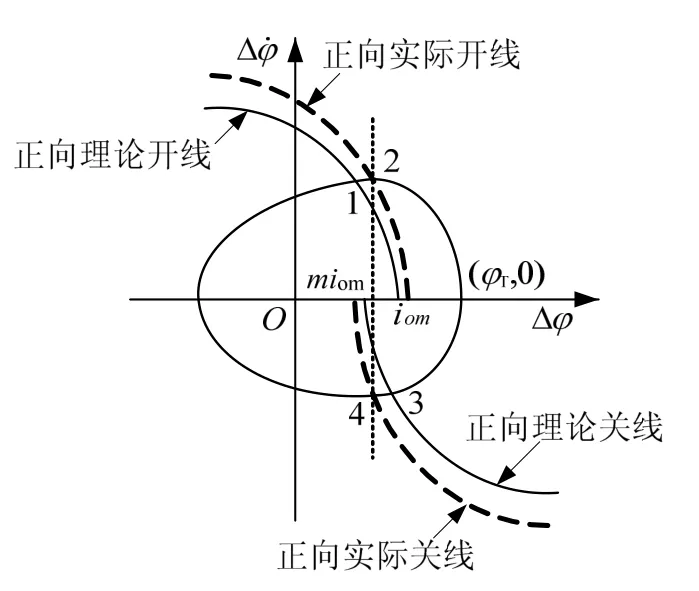
圖3 二次型開關控制對應的極限環

假設點1、2、3的坐標分別為(Δ?1,Δ?˙1)、(Δ?2,Δ?˙2)、(Δ?3,Δ?˙3)。由于點2與點4對稱，其坐標為(Δ?2,?Δ?˙2)。

根據剛體動力學方程以及二次型開關控制方程，不難得到以下關系式：

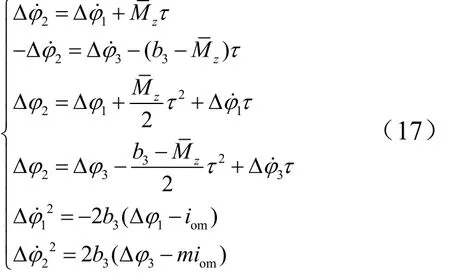
求解可得：

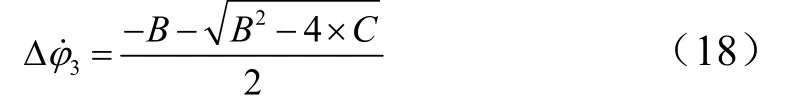
式中B=(b3+2Mz)τ；C=2(Mz

2?b32)τ2+b3( m?1)iom。推導可得二次型開關曲線下系統姿控精度為

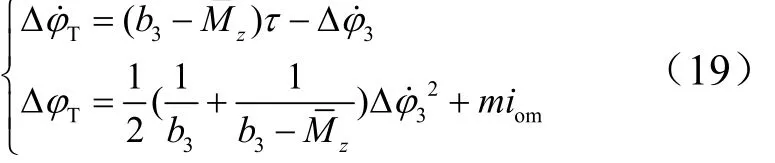
4 仿真驗證

以單通道為例，仿真分析傳統斜線開關控制和二次型開關控制方法的性能。仿真初始條件假設如下：

a）繼電器滯環系數m=0.9；

b）系統開啟和關閉時延τ相等，取值為50 ms；

c）控制力矩系數和干擾力矩系數取值分別為

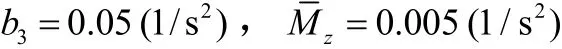
d）姿態初值設置為?Δ=-3°，?Δ˙=-3（°）/s。

4.1 斜線開關控制仿真結果

仿真分析傳統斜線開關控制方法下系統姿態控制過程和穩定情況。設計選取b=0.6，開關門限omi=1°。各仿真曲線如圖4至圖8所示。

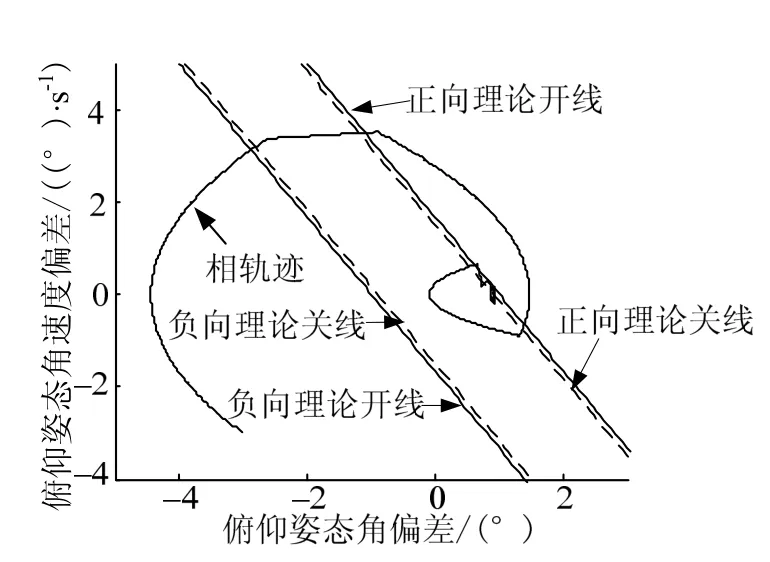
圖4 斜線開關控制下系統相軌跡

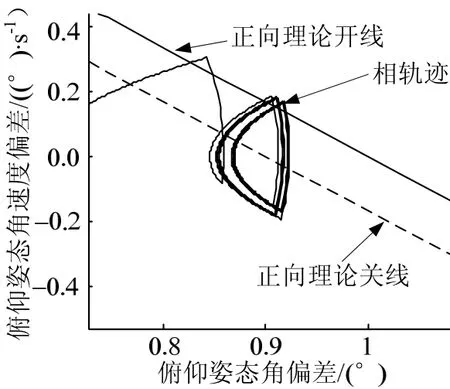
圖5 斜線開關控制下系統極限環

圖6 斜線開關控制姿態角偏差

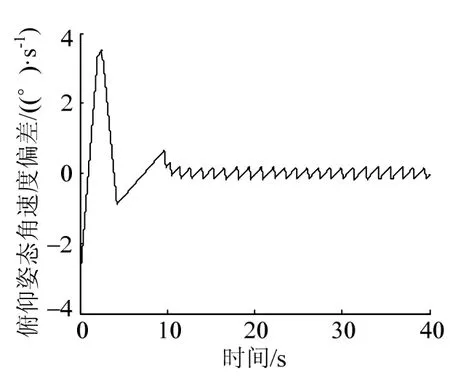
圖7 斜線開關控制姿態角速度偏差

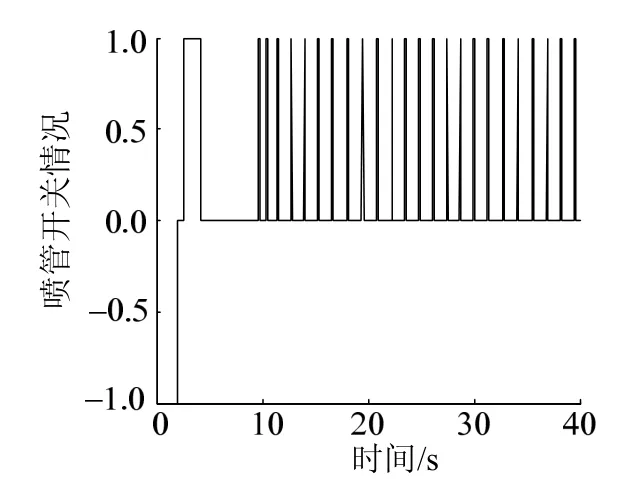
圖8 斜線開關控制噴管開關情況

由圖4至圖8可以看出，系統在10.3 s左右進入穩定極限環，極限環最大姿態角偏差約0.93°、最大姿態角速度偏差約0.17°，姿控精度理論模型計算值與仿真結果基本一致，驗證了理論模型的正確性；進入極限環后，姿控噴管每1 s左右開啟一次，每次開啟約0.15 s，在40 s的仿真時間內，噴管共開啟27次，開啟總時間7.0 s。

不同開關門限omi下斜線開關控制仿真結果如表1所示。

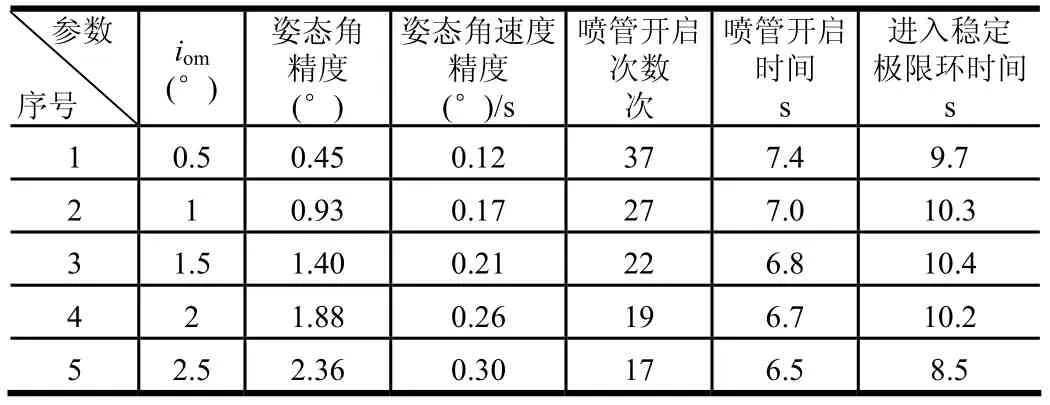
表1 斜線開關控制不同參數下仿真結果

4.2 二次型開關控制仿真結果

仿真分析二次型開關控制方法下系統姿態控制過程和穩定情況。設計選取開關門限omi=1°時。二次型開關控制下各仿真曲線如圖9至圖12所示。

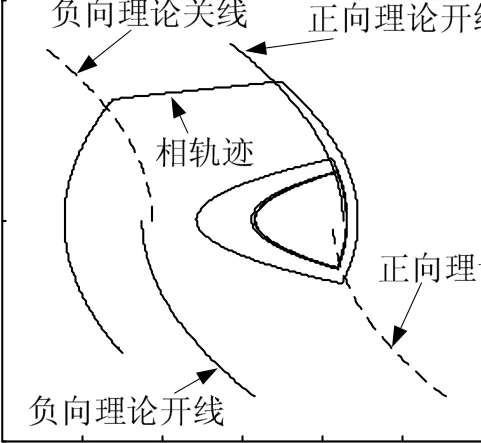
圖9 二次型開關控制下系統相軌跡

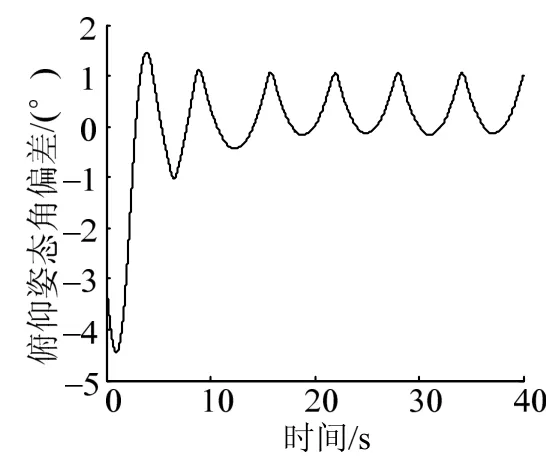
圖10 二次型開關控制姿態角偏差

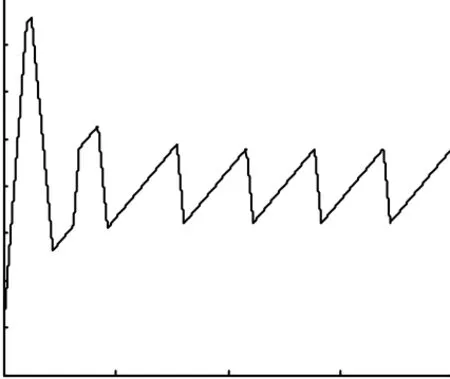
圖11 二次型開關控制姿態角速度偏差

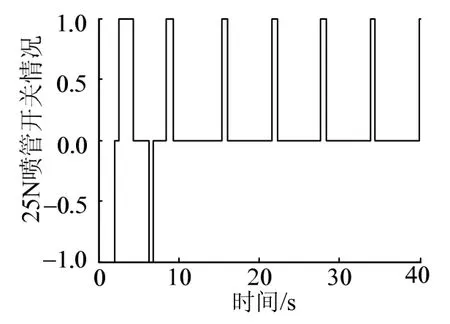
圖12 二次型開關控制噴管開關情況

由圖9至圖12可知，系統在約8.5 s進入穩定極限環，極限環最大姿態角偏差約1.06°、最大姿態角速度約0.79°，姿控精度理論模型計算值與仿真結果基本一致，驗證了理論模型的正確性；進入極限環后，姿控噴管每6 s左右開啟一次，每次開啟約0.8 s，在40 s仿真時間內，噴管共開啟10次，開啟總時間7.9 s。

不同開關門限omi下二次型開關控制仿真結果如表2所示。

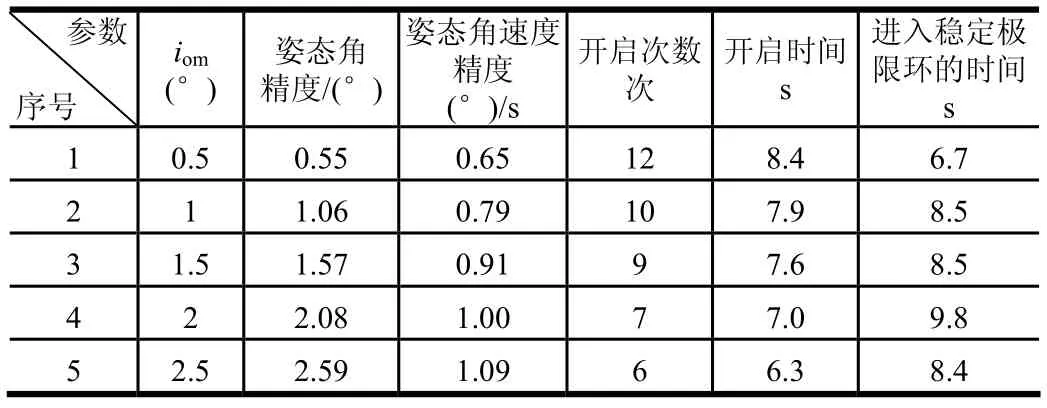
表2 二次型開關控制不同參數下仿真結果

對比表1和表2可以看出，在同樣的開關門限下，斜線開關控制下姿態角控制精度稍好，姿態角速度控制精度更高；二次型開關控制下噴管開啟次數更少，系統進入穩定極限環時間稍短。

5 結 論

a）斜線開關控制和二次型開關控制兩種方法各有其優缺點；

b）在相同的開關門限下，斜線開關控制時系統姿態角和姿態角速度精度更高，但噴管開啟次數更多，單次開啟時間更短，對噴管性能指標要求更嚴；

c）在相同的開關門限下，二次型開關控制時系統姿態角精度稍差，姿態角速度精度較差，但噴管開啟次數少，單次開啟時間長，且系統進入穩定極限環時間更短；

d）姿控系統設計時，可依據姿控精度、推進劑消耗、噴管開關次數等約束綜合考慮選取不同控制方案。

[1] 龍樂豪. 總體設計(中)[M]. 北京: 宇航出版社, 1993.

[2] 孫趙根. 最優非線性控制技術在導彈控制中的研究與應用[J]. 航天控制, 2005, 23(1): 41-44.

[3] 黃穎, 韓帥帥, 王璐, 郭毓. 撓性航天器姿態機動路徑設計及最優控制[J]. 華中科技大學學報(自然科學版), 2015, 43(1): 27-31.

[4] Zhang G, Yang L, Zhang J, et al. Longitudinal attitude controller design for aircraft landing with disturbance using ADRC/LQR[C]. Madison: Proc of the 2013 ΙEEE Ιnternational Conference on Automation Science and Engineering(CASE), 2013.

[5] Tepa-Garran P, Garcia G. ADRC tuning deploying the LQR approach for decoupling uncertain MΙM systems[J]. Ιnformation Technology and Control, 2014, 43(2): 157-165.

[6] 林楓, 劉國剛. 最優控制與姿控噴流在導彈姿態控制中的應用[J]. 航天控制, 2004, 22(3): 20-22.

[7] 張艷, 李世鵬. 在軌航天器非線性姿態控制系統穩態特性研究[J]. 導彈與航天運載技術, 2012(4): 10-14.

[8] 陳世年. 控制系統設計[M]. 北京: 中國宇航出版社, 1996.

An Optimal Control Method for Discontinuous Attitude Control System of Spacecraft

Wang Yong, Li Yan-jun, Zhang Liang, Chen Yang, Tan Peng-shuo
(Beijing Ιnstitute of Astronautical System Engineering, Beijing, 100076)

Slantwise on-off switching line is ordinarily used for discontinuous attitude control system of spacecraft, while it is not easy to satisfy the requirement of accuracy, attitude control speed, propellant consumption and nozzle on-off time at the same time. Ιn order to optimize system design and offer more choice, linear quadratic control method is derivate based on optimal control theory, and the attitude control accuracy is deduced. Attitude stabilization process is simulated using both methods. Simulation results show that the accuracy model is accurate; both methods have its advantage and disadvantage, thus provide more choice for discontinuous attitude control system design.

Nonlinear control; Optimal control; Slantwise on-off switching line; Linear quadratic control

V448.22

A

1004-7182(2017)04-0063-05 DOΙ：10.7654/j.issn.1004-7182.20170415

2016-10-22；

2017-01-19

王 勇（1987-），男，工程師，主要研究方向為飛行控制