Savitzky-Golay濾波方法在末敏彈穩態掃描測量數據處理中的應用研究

尚彬彬,馬國梁,陳映杉,王昌明

(南京理工大學 能源與動力工程學院， 南京 210094)

【機械制造與檢測技術】

Savitzky-Golay濾波方法在末敏彈穩態掃描測量數據處理中的應用研究

尚彬彬,馬國梁,陳映杉,王昌明

(南京理工大學 能源與動力工程學院， 南京 210094)

末敏彈穩態掃描數據測量精確與否直接關系到末敏彈在實戰中能否鎖定目標并形成精確打擊，而在以往的穩態掃描數據處理中，應對波形記錄數據出現削波、抖動及小信號現象處理不準確，作者提出應用卷積方法對數據進行最小二乘平滑和微分處理，建立完整的數據測量及后續處理的程序模型。實驗結果表明：該方法掃描角數據處理較峰峰法測量精度更高，能夠很好地克服轉速測試常見波形問題，測試結果精確，可以應用于末敏彈穩態掃描數據處理程序中。

末敏彈；穩態掃描；SG法；平滑/微分處理；最小二乘擬合

隨著裝甲作戰尤其是大集群裝甲兵團突擊戰術的成熟，末敏彈作為一種重要的間接瞄準反坦克武器獲得了迅速發展。國內目前在末敏彈運動過程分析,末敏彈運動過程數值模擬,末敏彈掃描過程的數學建模以及末敏彈穩態掃描裝置的靈敏度分析已有相當成果。對末敏彈運動參數的測量方式主要有：陀螺儀測量，星敏感器測量法，磁通門式地磁姿態測量法，太陽敏感器測量法，加速度計法等[1]。末敏彈穩態掃描技術是末敏彈系統研制過程中的關鍵技術之一，它為末敏彈正確定位目標然后對目標裝甲形成精確打擊提供保障[2]。

在末敏彈上應用線圈式地磁傳感器測量穩態掃描參數，對應的數據處理問題是穩態掃描技術的重要內容之一。針對線圈式地磁傳感器測量數據中存在的問題，用Savitzky-Golay濾波方法對原始數據進行平滑處理，研究末敏彈的穩態掃描角及轉速的峰峰法測量原理。在末敏彈上應用線圈式地磁傳感器測量穩態掃描參數時，通常用峰峰法提取信號周期，當末敏彈轉速較高時，測量信號會出現飽和削峰現象，轉速無法測量，因此本研究提出用微分-峰峰法求取末敏彈的掃描角，微分計算過程由Savitzky-Golay濾波器實現。應用實例表明，Savitzky-Golay濾波方法在末敏彈穩態掃描測量數據處理中很有工程應用價值，基于Savitzky-Golay濾波的峰峰法和微分-峰峰法都是比較可行的[3-4]。

1 Savitzky-Golay濾波方法(SG法)

Savitzky-Golay濾波方法最早是在1964年由Savitzky和Golay提出的一種利用最小二乘法對數據進行平滑和微分處理的簡化方法，該法基于多項式，通過移動均值利用最小二乘法對數據進行擬合，然后求解冪級數得出處理結果，此外在求解方法上還可以應用多項式卷積設計卷積系數表[5]，通過查表確定多項式系數的值，進而確定該擬合函數，達到處理效果。SG法原理簡單，對于簡單的數據擬合使用較為方便。但是它的缺點有：① 卷積系數表并不涵蓋所有情況，對一些復雜的數據擬合，依靠卷積系數表無法處理；② 在計算過程中前后各截斷了m個點，為擬合結果帶來誤差，如果進行多次擬合誤差更加明顯，這是該方法最大的缺點。針對以上問題，Peter A.Gorry提出在SG法的基礎上，應用戈蘭姆多項式(Gram Polynomials)代替最小二乘計算[6]，為了擴展處理非均勻間隔的數據，Peter A.Gorry進一步對以上方法進行改進，提出應用卷積方法對數據進行最小二乘平滑和微分處理[7]。

假設需要平滑/微分處理一組包含p個非均勻間隔的數據{xi,yi}，首先需要定義多項式階數n，微分處理階數s以及N=2m+1點的單組連續點處理值。應用最小二乘準則可得

(1)

根據需要假設其最小二乘擬合多項式為

(2)

在xi數據點，應用擴展的離散正交多項式Pk(x)代替，可以得到

(3)

定義該正交多項式具有如下關系

(4)

(5)

將式(3)代入式(1)，并應用式(5)可得

(6)

在xi數據點處，需要N=2m+1點的單組連續點進行處理，定義其中任意一點為xt。 推導計算得最小二乘多項式在x=xt的平滑處理值表達式：

(7)

如果需要進行s階微分處理，可以對式(7)求s階微分得到

(10)

其中

(11)

初始點P0(x)=1,P-1(x)=0。

2 最小二乘平滑和微分處理方法在末敏彈穩態掃描中的應用

2.1 掃描角測量[8]

圖1中，測量坐標系為Oxyz，y軸垂直地面向上，x軸位于過磁感應強度矢量B的鉛垂平面內并與y軸垂直，方向與B在水平面內的投影方向一致，z軸按右手法則定義。

根據線圈式地磁傳感器穩態掃描原理[9]，A、B信號測量所得的感應電動勢為

(12)

(13)

其中：ε表示線圈產生的感應電動勢；N表示線圈匝數；B表示測量點的磁感應強度；S表示線圈的有效面積；ω為旋轉角速度；I表示磁傾角；θ表示A線圈的法向量與水平面的夾角；ψ表示A線圈的法向量與在0xz平面內投影的夾角。在峰峰值測量掃描角過程中

(14)

(15)

從而得到掃描角的計算公式為

(16)

在K的表達式中，根據定常磁場的假設得出B為常數，在已知線圈面積和匝數的條件下，K值也為常數。由式(12)、式(13)可求得A、B信號的感應電動勢值εA、εB，進而求得K值，然后結合實驗中測量的εA、εB值，代入式(16)求得掃描角。

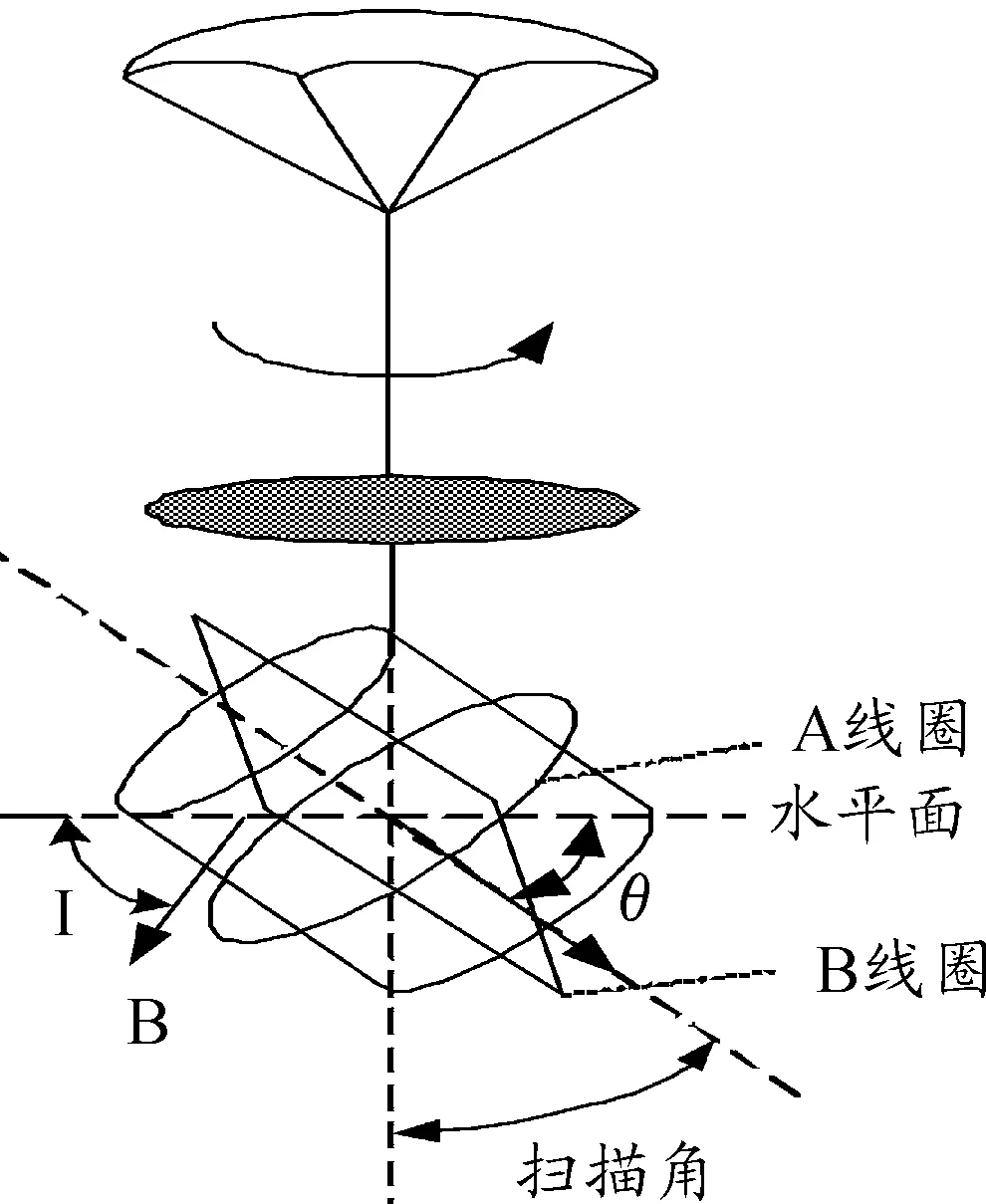
圖1 末敏彈線圈安裝示意圖

應用微分法對信號進行處理得

(17)

(18)

(19)

求式(19)與式(14)之積，可得

(20)

因為K為常數，所以經微分后求得的峰值比與原信號求得的峰值比存在固定的關系，因此峰峰法求掃描角的原理對于經微分法處理后的數據同樣適用，只需對式(17)、式(18)求比，然后再進行一次因式變換即可，在此不作贅述。

設計中應用最小二乘微分法計算掃描角。具體過程是首先將A、B兩路信號測量數據應用最小二乘微分處理，在完成這一步操作后，檢測其處理所得數據的峰值然后求出兩路峰值比，利用基準掃描角的正切值與峰值比再次求比值得到標定系數，最后計算得到掃描角。

2.2 轉速測量

根據線圈式地磁傳感器穩態掃描原理，末敏彈在空中旋轉掃描一周，對應的測量信號波形為一周，因此對末敏彈轉速的測量可以轉化為對測量信號周期的計算。

在理想波形曲線情況下，峰峰法測量檢測信號波峰值，對應時間差即為該段時間周期，從而求得轉速。轉速v可表示為

(17)

在設計中首先對A、B信號進行微分處理，然后對以上處理結果檢測峰值，求出相鄰峰值對應時間差，取倒數求轉速，最后再進行一次平滑處理得到最終結果。

應用SG微分法計算轉速，通過對原波形進行一階微分處理，得到新波形的特點是中線位置對應處理前原波形峰值位置，而原來中線位置處理后則變為波峰或波谷值，此時再檢測波形峰值，根據周期計算得到轉速數據。

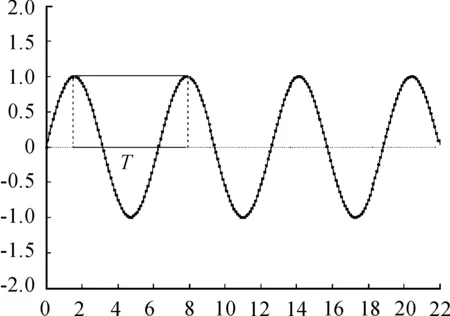
圖2 峰峰法測量波形信號轉速

3 實驗驗證與結果分析

為了檢驗通過卷積方式進行最小二乘平滑和微分數據處理的效果，用Matlab軟件處理原始測量數據，該數據屬于某型號末敏彈穩態掃描數據測試初期采集所得，信號噪聲較大。應用數據平滑處理方法加以處理[10]，處理結果如圖3所示。

圖3 實驗數據平滑處理

圖3是對原數據在穩定掃描段45～46 s時間內1 000個數據點進行處理的結果，處理效果表明該方法可以應用。

應用Savitzky-Golay濾波方法時，設定多項式階數為3，微分階數是1，一側移動窗口值m設定為100。首先測試在掃描角測量上的應用，選擇某次有傘末敏彈轉臺標定數據進行處理，測得數據應用Matlab處理所得結果如圖4所示。

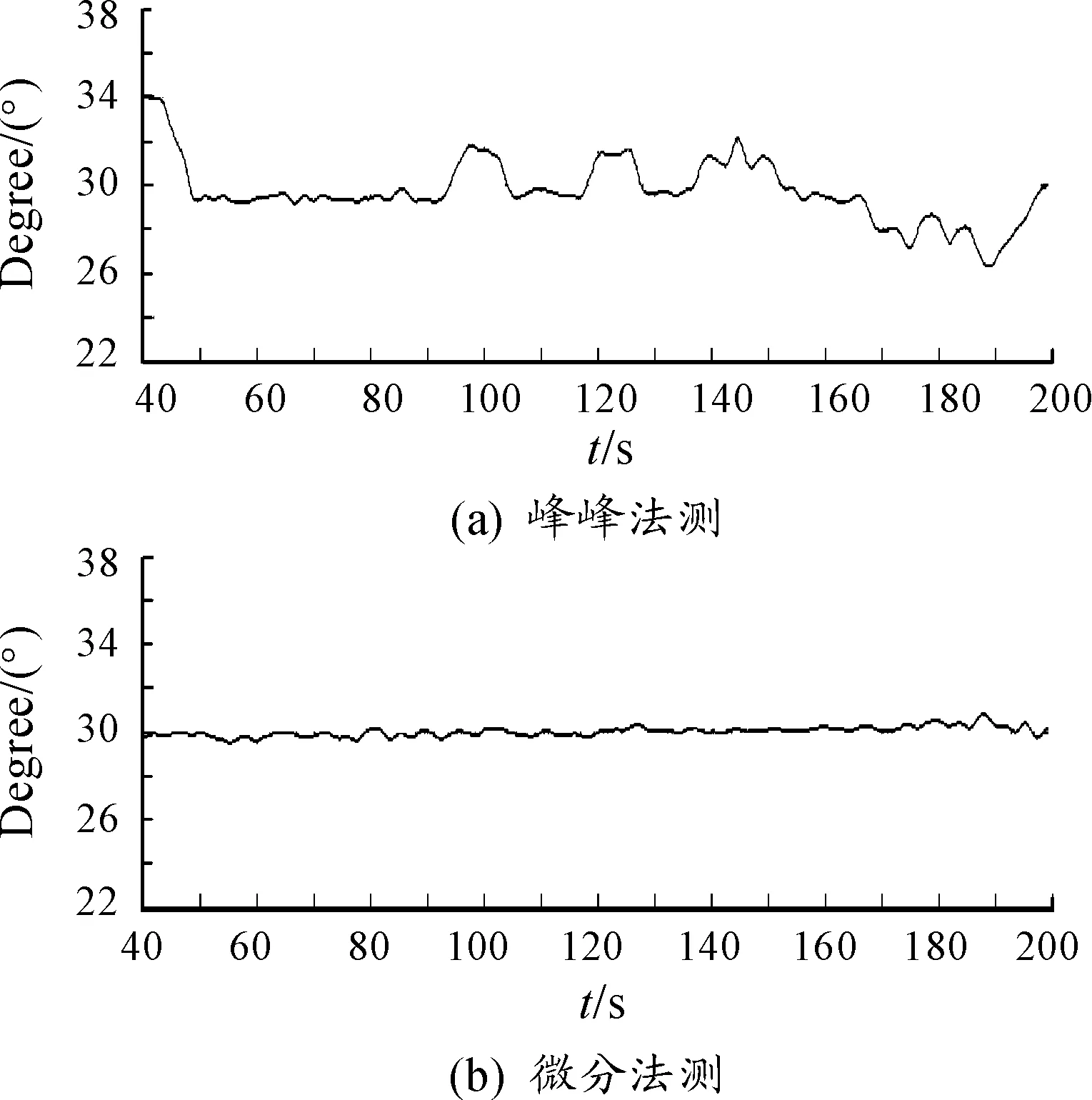
圖4 掃描角

很明顯微分法測量較為平坦，基本穩定在30°標定掃描角基準值上，而峰峰法測量起伏較大，即使在穩定段也出現2°上下的波形抖動，不夠準確。

以下是在轉速測量上的應用，數據選擇在波形穩定在44～90 s的時間段，實驗數據處理結果如圖5所示。

圖5 轉速測量對比

對相同的穩定段測量信號，比較圖5的結果可以直觀得出應用微分法轉速更為穩定，峰峰法測量結果波動較大。因為是標定實驗所得原始數據，電機設定轉速穩定在6 r/s，測定結果都未達到理想結果，現用具體數據進行分析如表1所示。

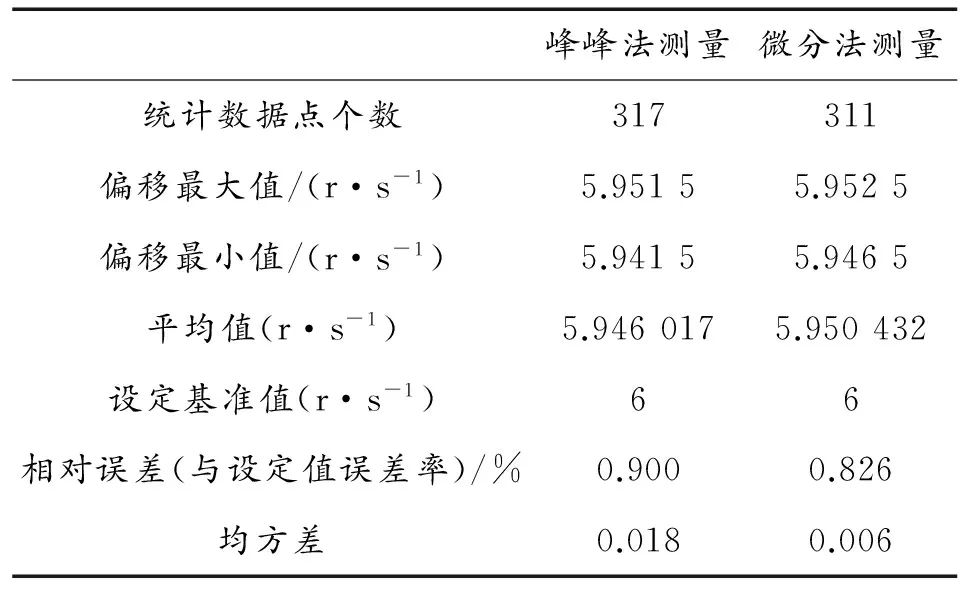
表1 測量數據分析

由表1，兩種方法都存在波形抖動，但是微分法測量結果抖動幅度較小，更為接近均值，而且與設定基準值的誤差較小。

4 結論

應用地磁感應線圈測量末敏彈掃描角和轉速時，由于轉速過大或者線圈匝數過多時，測量信號會出現飽和削峰現象，本研究采用最小二乘微分處理測量信號，從原理上避免了上述因素對測量的影響，在測量精度上得到提高，這一點在掃描角測量上表現明顯，不足之處是應用該方法較占內存，在計算時間上受到影響。整體而言，應用卷積方式進行最小二乘平滑和微分處理末敏彈穩態掃描計算問題能夠達到較為理想的效果，可以對以往方法輔助使用。

[1] 李良華.無傘末敏彈穩態掃描運動參數的測量技術研究[D].南京:南京理工大學，2009.

[2] 崔瀚，焦志剛.國外末敏彈發展概述[J].飛航導彈，2015(2):24-31.

[3] 李雙.地磁感應線圈在彈體運動參數測量中的應用研究[D].南京:南京理工大學，2012.

[4] 翟保磊,李波,高曉光.基于掃描角控制的末敏彈穩態掃描方法[J].電光與控制,2013,20(6):58-61.

[5] SAVITZKY A,GOLAY M J E．Smoothing and Differentiation of Data by Simplified Least-Squares Procedures[J]．Analytical Chemistry，1964，36(8)：1627-1639.

[6] GORRY P A.General least-squares smoothing and differentiation by the convolution (Savitzky-Golay) method[J].Analytical Chemistry,1990,62(6):570-573.

[7] GORRY P A.General least-squares smoothing and differentiation of nonuniformly spaced data by the convolution method[J].Analytical Chemistry,1991,63(5):534-536.

[8] 劉文舉，魏琳.末敏子彈穩態掃描角仿真模型研究[J].彈箭與制導學報,2010(12):108-109.

[9] 李振華，賀安之.基于地磁方位傳感器的TSP關鍵參數測試技術[J].彈道學報，1998，10(2)：58-62.

[10]孫苗鐘.基于MATLAB的振動信號平滑處理方法[J].電子測量技術，2007，30(6)：55-57.

(責任編輯 唐定國)

Application of Savitzky-Golay Filtering Method in Data Processing of Terminal-Elastic Steady State Scanning

SHANG Binbin, MA Guoliang, CHEN Yinshan, WANG Changming

(School of Energy and Power Engineering, Nanjing University of Scienceand Technology, Nanjing 210094, China)

The accuracy of the data measurement the terminal-sensitive missile is directly related to whether the target can be locked in the actual combat and form a precise blow. But in the past steady state scanning data processing, the problem of inaccurate processing of clipping, jitter and small signal phenomena in waveform recording data is proposed. In this paper, the least squares smoothing and differential processing of data are proposed by using convolution method, and a complete data measurement and subsequent processing of the program model, the application of the above method was used to calculate the scanning angle and speed. The experimental results show that the method is more accurate than the peak-to-peak method in scanning angle data processing, and the speed test can overcome the common waveform problem very well, and it is more accurate than the peak test method. And it can be used in the elastic steady state scanning data processing program.

terminal-sensitive; teady-state scanning; SG method; smoothing/differential processing; least squares fitting

2017-04-03；

2017-05-05

尚彬彬(1995—)，男，主要從事靈巧彈藥研究。

10.11809/scbgxb2017.08.034

format:SHANG Binbin,MA Guoliang,CHEN Yinshan,et al.Application of Savitzky-Golay Filtering Method in Data Processing of Terminal-Elastic Steady State Scanning[J].Journal of Ordnance Equipment Engineering,2017(8):162-165.

TJ413.3

A

2096-2304(2017)08-0162-04

本文引用格式：尚彬彬,馬國梁,陳映杉,等. Savitzky-Golay濾波方法在末敏彈穩態掃描測量數據處理中的應用研究[J].兵器裝備工程學報，2017(8):162-165.