縱向振動對捷聯慣導誤差影響半解析表達式研究
楊 其,蘇國華,劉慶寶,劉新學
(1.火箭軍工程大學 士官學院, 山東 青州 262500; 2.火箭軍裝備研究院, 北京 100085;3.火箭軍工程大學 初級指揮學院, 西安 710025)
【裝備理論與裝備技術】
縱向振動對捷聯慣導誤差影響半解析表達式研究
楊 其1,3,蘇國華2,劉慶寶1,劉新學3
(1.火箭軍工程大學 士官學院, 山東 青州 262500; 2.火箭軍裝備研究院, 北京 100085;3.火箭軍工程大學 初級指揮學院, 西安 710025)
針對實際動態工況條件下捷聯慣導輸出與靜態條件下輸出存在一定誤差的問題,在僅考慮縱向振動的條件下,將飛行器儀器艙內的慣導系統等效為桿與阻尼彈簧振子的組合系統,利用復模態分析方法使方程解耦,并推導了動態擾動環境中慣導加速度響應的半解析表達式,給出了實際敏感加速度的包絡范圍,指出捷聯慣導加速度計敏感值變為圍繞真實值分布的隨機變量是動態環境條件下產生加速度誤差的根本原因之一。
縱向振動;捷聯慣導;加速度計;動態誤差
從材料力學角度來看,固連于飛行器儀器艙的捷聯慣導不可能以絕對剛體運動反映出飛行器的運動狀態[1,2],大量試驗和仿真表明捷聯慣導靜態實驗室環境下的輸出與動態條件下的輸出存在一定誤差[3-5],在導航解算算法默認慣導輸出完全準確的前提下,從本質上就產生了測量誤差。更為科學的方法應該將其考慮為組合線彈性系統,考慮在飛行器飛行過程中受到附面層壓力波動等隨機輸入時線性系統的響應輸出。研究在僅考慮縱向振動的情況下,將捷聯慣導等效為桿與阻尼彈簧振子組合線性系統,分析隨機輸入時捷聯慣導加速度計誤差的形成機理。
1 等效模型描述
捷聯慣導在設計安裝過程中,為了盡量減小外界振動對儀器帶來誤差并確保使用中正確安裝,一般設計有橡膠墊和安裝支架等系統,其安裝方式如圖1所示。
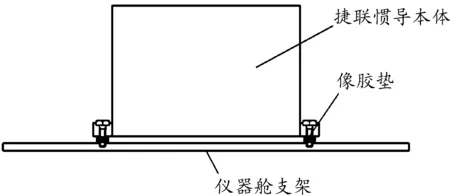
圖1 捷聯慣導安裝示意圖
工程實際中采用的安裝方式在理論上具有無窮多個運動自由度,可在任意方向等效設置阻尼彈簧系統,為了使機理分析更清晰,屏蔽運動方程其余方向上的耦合運動,模型假設僅考慮縱向振動,將儀器艙支架等效為長度為l的桿,并假設連接點具有絕對剛度,系統等效結構圖如圖2所示。
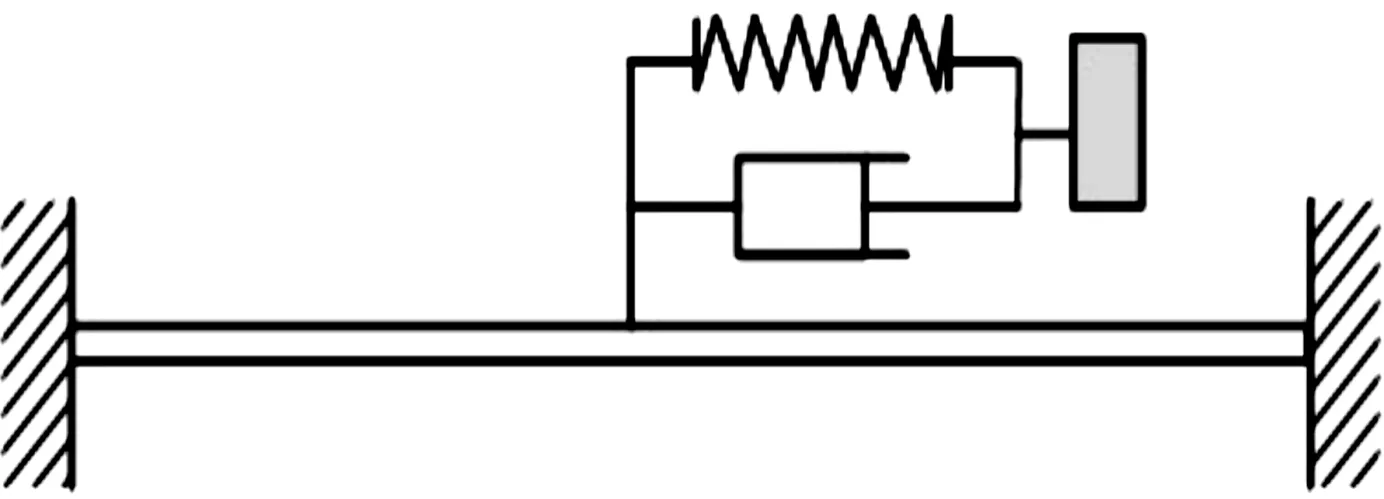
圖2 等效桿與阻尼彈簧振子組合系統
2 組合系統運動微分方程
桿的縱向受迫振動在結構動力學領域內已形成經典成熟理論,其運動微分方程為[6-7]
(1)
式中:桿長為l;材料密度為ρ;橫截面積為A;材料彈性模量為E;縱向位移為u(x,t);桿的縱向分布力為q(x,t)。
假設桿的兩端固支,縱向分布力為常量F,初始條件均為0,可得到縱向桿的響應為
(2)
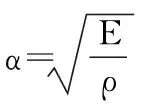
設阻尼彈簧振子安裝于桿上的xi位置,則此時阻尼彈簧振子的運動微分方程為
(3)
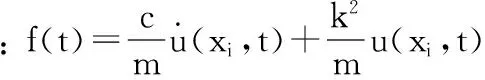
3 復模態分析
由于飛行器所承受的動態環境多呈現隨機性,即對于等效系統輸入的激振力并不能以確定性函數的形式表示,而是以隨機過程描述,但根據力學隨機振動理論,研究更為關心的是響應過程的數字特征[8]。
為了明確分析動態環境對慣導加速度計影響的機理,更應關注的物理量為組合系統中等效于本體的等效質量在桿的縱向產生的響應加速度,該響應直接由加速度計敏感并引入導航解算流程[9]。
引入狀態變量
將式(3)改寫為矩陣形式,可得

(4)
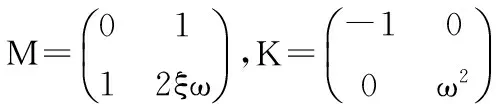
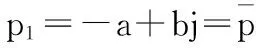
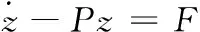
(5)
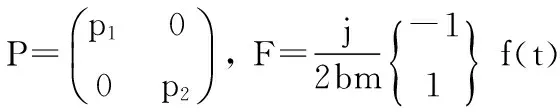
此時方程已解耦,由杜哈梅積分可以得到復模態響應z的平穩解
(6)
式中,hi(t)=epit,表示系統脈沖響應函數。
對于該組合系統其激勵主要來自飛行過程中飛行器機體所產生的擾動,為了使激勵-響應關系便于求解,不失一般性地假設受到的擾動為平穩隨機激勵[9],其協方差函數為
(7)
此時復模態響應的協方差函數可表示為
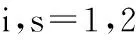
(8)
由式(5)可得
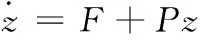
(9)
因此
(10)
進而根據復模態變換式并對其求導數,可以求得系統在縱向響應加速度的協方差函數為
(11)
當τ=0時,式(11)表示捷聯慣導本體在受到平穩隨機激勵時,產生縱向加速度響應的方差。這一擾動加速度是動態環境中加速度計產生誤差的根本原因之一。
4 影響機理分析
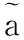
5 結論
1) 研究在僅考慮縱向振動的前提下,將飛行器儀器艙內的捷聯慣導系統等效為連續桿與離散阻尼彈簧振子組成的組合系統。
2) 通過分析等效桿與阻尼彈簧振子混合系統微分方程,可以看到在外部出現隨機激勵的情況下,使捷聯慣導加速度計敏感值變為圍繞真實值分布的隨機變量,這是動態環境造成加速度誤差的根本原因之一。
3) 在一定假設條件下,利用復模態分析法對組合系統微分方程解耦,并推導了加速度響應的半解析表達式,對該模型的求解在已知縱向桿邊界條件格林函數表達式的情況下,也可以利用格林函數法進行求解。
4) 僅考慮縱向振動的等效模型與設備的實際工況仍有較大差距,如果考慮支架的橫向振動和扭轉則需要將其考慮為歐拉梁和鐵木辛柯梁,同時連續桿的響應表達式在使用時還需截斷進行數值計算,所以模型并不適用于工程問題的直接求解,但模型用于分析動態環境對于捷聯慣導誤差的影響機理有很好的支撐作用。
[1] 謝燕.慣導支架結構的隨機動力響應分析與參數優化[D].長沙:國防科技大學,2004.
[2] 付繼波,馬靜,晁建軍.彈性支撐慣導系統振動耦合問題研究[J].強度與環境,2005,32(2):46-51.
[3] MICHAEL A.BLENDER,HEIDI WILKIN.Flight dynamics of a hypersonic vehicle during inlet un-start[C]//16th AIAA/DLR/DGLR International Space Planes and Hypersonic System and Technologies Conference.AIAA-2009-7292.
[4] PAUL G.SAVAGE.Analytical modeling of sensor quantization in strapdown inertial navigation error equations[J].Journal of Guidance,Control and Dynamics,2002,25(5):833-842.
[5] 張希農,李智明.火箭儀器艙儀器安裝板的振動控制試驗研究[J].宇航學報,2002,23(1):76-78.
[6] 朱位秋.隨機振動[M].北京:科學出版社,2016.
[7] 劉習軍,賈啟芬,張素俠.隨機理論及工程應用[M].北京:機械工業出版社,2015.
[8] 方同.工程隨機振動[M].北京:國防工業出版社,1995.
[9] 吳曉.長航時高精度捷聯慣導系統誤差抑制技術研究[D].哈爾濱:哈爾濱工程大學,2011.
[10]趙翔.多場耦合環境下梁橫向振動的半解析解[D].成都:西南交通大學,2015.
(責任編輯 周江川)
Semi-Analytic Function of SINS Error Under Longitudinal Vibration Condition
YANG Qi1,3, SU Guohua2, LIU Qingbao1, LIU Xinxue3
(1.Sergeant College, the Rocket Force University of Engineering, Qingzhou 262500, China;2.The Rocket Force Equipment Research Institute, Beijing 100085, China;3.Primary Command College, the Rocket Force University of Engineering, Xi’an 710025, China)
Focusing on the SINS error between dynamic and static environment, the strap-down inertial system was equivalent to rod with damping spring vibrator system, which is considered under the hypothesis premise of exist only longitudinal vibration, and differential equation was decoupled with complex modal analysis, and the SINS error semi-analytic function under dynamic environment and the acceleration envelope range was deduced, and it finds out that the root cause of SINS error is the acceleration changed to a random variable around the true value under dynamic environment.
longitudinal vibration; strap-down inertial navigation; accelerometer; dynamic error
2017-04-22;
2017-05-20
楊其(1983—),男,博士研究生,講師,主要從事飛行器動力學與制導研究。
10.11809/scbgxb2017.08.004
format:YANG Qi, SU Guohua, LIU Qingbao, et al..Semi-Analytic Function of SINS Error Under Longitudinal Vibration Condition[J].Journal of Ordnance Equipment Engineering,2017(8):14-16.
V448
A
2096-2304(2017)08-0014-03
本文引用格式:楊其,蘇國華,劉慶寶,等.縱向振動對捷聯慣導誤差影響半解析表達式研究[J].兵器裝備工程學報,2017(8):14-16.

