基于散亂數據的二元樣條)曲面重構方法

汪春曉，路 游

(中國石油大學(北京),北京 102249)

汪春曉，路 游

(中國石油大學(北京),北京 102249)

在計算幾何領域中，利用曲面擬合散亂數據點集，是計算機圖形學以及計算機輔助幾何設計中一個困難的問題。傳統的基于均勻2-型三角剖分的二元樣條曲面重構算法存在重構速度較慢、曲面精度不高等問題。針對上述問題，提出了一種新的曲面重構方法。該方法通過數據點構造以卷積形式表示的控制系數，并構造迭代公式，迭代計算數據點與曲面的距離，根據距離調整控制系數，直到前后兩次數據點到曲面的最大距離的差值小于適當的閾值，進而確定最佳的控制系數，通過將點置于數據塊中，以數據塊為單位進行計算，采用取整的方式消除邊界處的重復計算，減少了重構曲面的計算次數。實驗結果表明，該方法提高了曲面重構的速度和質量，證明了此方法是可行、有效的。

二元樣條；卷積；曲面重構；控制系數；迭代方法

0 引 言

樣條函數，是具有一定光滑性的分段或者分片定義的多項式函數。在計算機幾何領域與飛機、船舶制造等領域均有重要的應用。一元樣條應用最早、最廣泛，研究的最詳細的是3次樣條函數。1946年，數學家I．J．Schoenberg系統地建立了一元樣條函數的理論基礎[1]。從60年代開始，樣條函數有了迅速的發展和應用。1966年，H.B.Curry和I.J.Schoenberg提出了一元B樣條函數，是一種定義B樣條函數的幾何直觀方法[2]。1975年，利用函數論和代數幾何方法，王仁宏教授構建了多元樣條函數的基本理論框架，開創了一套研究多元樣條函數基本問題的新方法，即光滑余因子協調法[3]。目前在多元樣條的研究方法上大致可分為三類：光滑余因子協調法，以王仁宏為代表；B-網方法，以Farin[4]為代表；B-樣條方法，亦稱投影子法，以Schoenberg[2]、de Boor[5]和Micchelli[6]等為代表。最近一段時間，樣條函數方面也有許多研究成果。文獻[7-8]分別介紹了多元樣條的應用研究，B樣條在模糊系統中的應用，等等。在文獻[9-13]分別介紹了B樣條的圖像插值方法，B樣條的數值流形和時間積分方法。

曲線曲面造型是計算機圖形學、計算機輔助幾何設計和計算機輔助設計所研究的重要內容，多元樣條在其中有重要的作用。到目前為止，曲線曲面造型以逐漸形成了以非均勻有理B樣條設計和隱式代數曲面為主體，以插值、擬合、逼近等方法為骨架的理論體系[3,14]。傳統的基于均勻2-型三角剖分二元樣條曲面重建方法構造的曲面具有內置的連續性，重建后的曲面整體次數低，控制頂點相對較少，曲面拼接時無需考慮拼接處的光滑問題，同時，曲面也具有良好的幾何和逼近性質，如幾何不變性、變差縮減性等。但是，該方法也存在一些不足，比如重構曲面的速度較慢，數據點與重構曲面之間的距離過大等。

針對以上問題，提出了一種新的非張量積型二元樣條曲面重構方法，通過卷積形式表示控制系數，結合數據點得到初始的控制系數，并構造迭代公式，迭代計算數據點與擬合曲面的距離，根據距離重新調整控制系數，直到前后兩次數據點到曲面的最大距離的差值小于給定閾值，最后通過最佳的控制系數進行曲面重構。

1 算法基本原理

1.1 均勻2-型三角剖分上二元樣條函數空間

均勻2-型三角剖分是在矩形剖分的基礎上，連接其中各小矩形的兩條對角線而形成的三角剖分，如果矩形剖分是均勻剖分的，那么，形成的均勻2-型三角剖分也是貫穿剖分[15]。

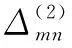
mx-i=0,ny-i=0,ny-mx-i=0,ny-mx-

i=0

其中，i=…,-1,0,1,…。

圖1 區域D及其剖分

每個內網點均由四條直線相交而成，如式(1)所示[16]：

Ni>(k+1)/(k-μ)

(1)

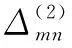
k>(4μ+1)/3

(2)

當μ一定時，則要求多項式的次數盡可能低，那么可以得到如下若干個均勻2-型剖分上的樣條函數空間：

利用貫穿剖分上的樣條函數空間維數公式[16]：

(3)

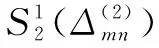
圖2 區域Q及其剖分

對各i=1,2,…,25，剖腔上的多項式可表示為：

根據對稱性原則可以推出其他剖腔上的多項式。

記Β(x,y)為圖2中定義在Q上的分片多項式，在編號為i的剖腔上記為pi，那么顯然Β(x,y)C1(2)，并且在Q內部Β(x,y)>0。因此，Β(x,y)是上的樣條函數，并且由文獻[17-18]可知，Β(x,y)的支集是最小的。

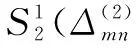
(4)

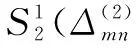
由式(4)定義的二元樣條函數A滿足：

(5)

對任意的i0,j0,0≤i0≤m+1,0≤j0≤n+1，集合Ai0,j0={Bi,j(x,y)A:(i,j)≠(i0,j0)}，構成了樣條函數空間的一組基底。

A中的二元樣條函數具有如下性質：

(6)

1.3 構造擬插值算子

（1）港口岸線資源整合和港區功能布局優化，推進港口集約化發展。由于碼頭性質、經營等方面的原因，杭州港存在著泊位利用效率不高，岸線使用效益差，部分港區功能布局分散等現象。本次港口總體規劃的編制，將按照岸線資源利用集約化和港口發展規模化、大型化和專業化的要求對岸線資源進行整合利用，對港區和泊位功能進行調整。總體規劃中處理好既有泊位與規劃新建泊位的關系，實現港口岸線資源整合和港區功能布局優化將是杭州港總體規劃編制工作的難點之一。

(7)

(8)

(9)

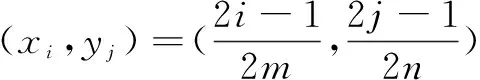
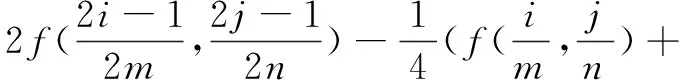
(10)

對于以上兩種擬插值算子有以下結論[17]：

(11)

1.4 優化控制系數

由控制系數表達式(見式(10))可知，控制系數與每一個數據塊周圍的四個數據點以及中心點的值有關，如圖3所示。

圖3 四個數據點及中心點

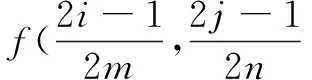
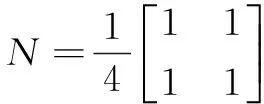
(12)

由于初始控制系數矩陣是預估值，會存在偏差，所以要對其進行修正。

E:=S-F

(13)

(14)

1.5 劃分邊界點

由式(9)可知，曲面W(f)由λi,j(f)和Bi,j(x,y)決定，由式(4)可知，Bi,j(x,y)是由B(x,y)在水平和垂直方向上進行平移得到，并且最終得到的曲面的定義域I?2。

需要對?(x,y)2定義其所屬的塊編號(i,j)，(i,j)∈2，如圖4所示。令：

(?x」,?y」)=(i,j)，(x,y)(?x」,?y」)

(15)

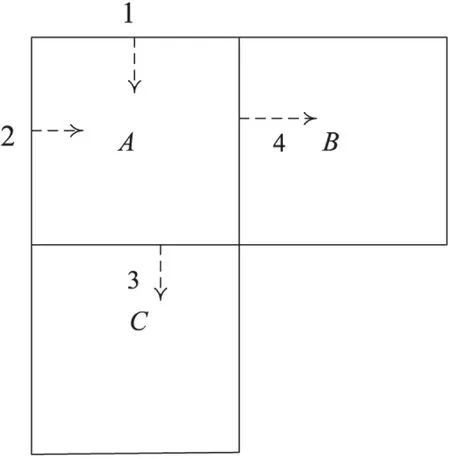
圖4 邊界處點劃分方法

這樣，?(x,y)∈2都有唯一的編號。可記為：{(?x」,?y」)|?(x,y)∈[1,m+1)×[1,n+1),m,n∈}={(?x」,?y」)|?(x,y)∈[1,m]×[1,n],m,n∈}。

2 算法實現過程

輸入：給定數據點集F，閾值τ，數據點距離曲面最大距離e1，前一次的數據點距離曲面最大距離e0。

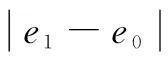
步驟4：在曲面上取與給定數據點坐標相同的點，根據式(13)計算其與給定數據點之間的最大距離ek，令e1=ek。

步驟6：輸出曲面W。

通過推導和分析可知，當輸入點為m×n時，總計算時間為Θ(l×m×n)，其中l為迭代次數，與曲面結構有關。

3 實驗結果

用Matlab軟件在處理器為Intel-1.80 GHz，內存為4.0 GB的普通個人電腦上分別利用傳統非張量積型曲面重構方法和文中提出方法進行曲面重構，結果如圖5所示。

(a)原始曲面

(b)在原始曲面上獲取的數據點

(c)傳統)方法重構出的曲面

(d)利用文中方法重構出的曲面

曲面重構各參數如表1所示。

表1 曲面重構數據參數表

4 結束語

針對傳統的非張量積型二元樣條曲面重構速度較慢、曲面精度不高等問題，提出新的非張量積型二元樣條曲面重構方法，通過重新構造控制系數，并利用迭代公式不斷修正控制系數，進而得到符合要求的最佳控制系數，使得重構出的曲面質量得到提高。在重構過程中，劃分點與塊的歸屬關系，將原來計算點的過程轉化為計算塊的過程，并且降低邊界處點的重復運算，減少了計算次數，降低了運算量，從而提高了重構曲面的速度。最后通過實驗證明了文中方法的可行性。

[1] Schoenberg I J.Contribution to the problem of application of equidistant data by analytic functions[J].Quart. Appl. Math,1946,4:45-99.

[2] Curry H B，Schoenberg I J．On Polya frequency functions IV:the fundamental spline functions and their limits[J]．J. Analyse Math,1996,17:71-107.

[3] 王仁宏.多元齒的結構與插值[J].數學學報,1975,18(2):91-106.

[4] Farin G.Bezier polynomials over triangles and the construction of piecewise Cr polynomials[R]．Brunel:University of Uxbridge,Middlesex,1980.

[5] de Boor C.Spline as linear combination of B-spline[M]//Approximation theory II.New York:Academic Press,1976:1-47.

[6] Dahmen W，Micchelli C A．Recent progress in multivariate splines[M]//Approximation Theory IV.New York:Academic Press,1983.

[7] 郭慶杰．多元樣條若干理論與應用研究[D]．大連:大連理工大學,2015.

[8] 譚彥華，李洪興，馬秀娟，等．B樣條函數在模糊系統中的應用[J]．控制理論與應用,2013,30(11):1445-1456.

[9] 魏曉靜．基于B樣條函數的圖像插值方法研究[D]．大慶:東北石油大學,2014.

[10] 溫偉斌．基于B樣條插值的數值流形方法與時間積分方法的研究[D]．重慶:重慶大學,2014.

[11] Zeng Xiaoming,Zhou Guorong,Yang Lianqiang.Best bounds on the distance between 3-direction quartic box spline surface and its control net[J]．Applied Mathematics:A Journal of Chinese Universities,2013,28(2):147-157.

[12] 楊聯強，王 東．三向四次箱樣條曲面與Bezier曲面的光滑拼接[J]．計算機工程與應用,2013,49(23):119-121.

[13] Fang Meie,Lu Jia,Peng Qunsheng．Volumetric data modeling and analysis based on seven-directional box spline[J]．Science China:Information Science,2014,57(6):1-14.

[14] 施法中．計算機輔助幾何設計與非均勻有理B樣條：CAGD&NURBS[M]．北京：北京航空航天大學出版社,1994.

[15] 王仁宏,崔錦泰.關于一個二元B樣條基[J]．中國科學,1984(9):12-23.

[16] Chui C K,Wang R H.Multivariate spline spaces[J].Jour. Math.Anal. Appl.,1983,94:197-221.

[17] 王仁宏，施錫泉，羅鐘鉉，等．多元樣條函數及其應用[M]．北京：科學出版社,1994.

[18] Wang R H.The dimension and basis of spaces of multivariate splines[J].Journal of Computational and Applied Mathematics,1985,12(85):163-177.

WANG Chun-xiao，LU You

(China University of Petroleum，Beijing 102249，China)

In the field of computation geometry,the use of surface fitting scattered data points is a difficult problem for CG and CAGD.The traditional bivariate spline surface reconstruction algorithm based on uniform type-2 triangulation exists shortcomings of slow speed and poor accuracy.Aiming at these problems above,a new surface reconstruction method is developed successfully.The convolution type control coefficient is offered through the data points,and the distance between data points and surface is obtained by iterative method.Then according to the distance,control coefficient is adjusted until the difference is less than the appropriate threshold before and after the maximum distance of data points and surface,so the optimum control coefficient is determined.Then blocks are selected as basic calculation unit,eliminating repeated calculation at the boundary reduced computation times.The results show that the method improves the speed and quality of surface reconstruction and is proved to be feasible and effective.

bivariate spline；convolution；surface reconstruction；control coefficient；iteration method

2016-08-27

2016-11-30 網絡出版時間：2017-06-05

國家自然科學基金資助項目(60873093)

汪春曉(1991-)，男，碩士生，研究方向為計算機可視化、計算幾何；路 游,博士，副教授,研究方向為計算幾何、圖形學、虛擬現實。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170605.1508.052.html

TP391

A

1673-629X(2017)08-0025-05

10.3969/j.issn.1673-629X.2017.08.006