半柔性聚合物中剛性系數Kbend對體系影響的Monte Carlo模擬研究*

肖立勇 紀登輝

(六盤水師范學院電氣工程學院 貴州 六盤水 553004)

半柔性聚合物中剛性系數Kbend對體系影響的Monte Carlo模擬研究*

肖立勇 紀登輝

(六盤水師范學院電氣工程學院 貴州 六盤水 553004)

結合自洽場理論的粒子數表象到場表象思想，運用蒙特卡洛模擬方法對半柔性聚合物體系進行計算模擬．對于一個半柔性聚合物體系，其體系的哈密頓量主要包括鍵與鍵之間的鍵能、體積排斥能和彎曲彈性能，其中的鍵能用彈性能來表示，體積排斥能可通過粒子表象到場表象轉化的密度場來描述，單鏈聚合物的彎曲彈性能可以剛性系數Kbend來表述．通過計算模擬發現：1.在稀溶液中的單鏈聚合物體系中，其回旋半徑(Rg)和末端距(R0)隨著彈性系數的增加而增長；2.在高濃度的聚合物體系中，其回旋半徑和末端距不隨彈性系數的變化而變化，其投影長度(Ls)隨著彈性系數的增加而增加；3.投影長度與單鏈聚合物的聚合度N的a倍成正比，與彈性系數Kbend的b次方成正比，且a≈b≈0.4±0.45；4.投影長度的與體系中聚合物的濃度無關．

半柔性聚合物 場表象 投影長度 蒙特卡洛模擬

1 引言

半柔性聚合物在自然和生活中領域扮演著重要角色，半柔性聚合物的性質在一定程度上和一般的柔性聚合物相似，如能夠自組裝成各種相態等[1～6]，同時又有自身的性質，如具有一定的剛性，如DNA分子等．對于半柔性聚合物，在天然和人工合成中，如多肽、烷基取代纖維素等，具有溫度響應性，同時根據半柔性聚合物的耐熱性、加工性優異性，在電子、汽車部件等領域得到廣泛的應用[7～15]．在理論研究方面，C.M. Chen等[9]用Monte Carlo模擬半柔性聚合物剛性系數對鏈折疊動力學產生重要的影響，其發現隨著鏈的剛性系數的增強，其相態出現許多缺陷，同時Jianhui Song等[10]用格子Monte Carlo模擬一個半柔性ABA三嵌段共聚物的相行為，通過研究發現不同剛性的聚合物對聚合物的相圖有很大影響．同時還有Wendi Song等[1～2]用一種新的現實空間數值實現自洽場理論對聚合物的研究和用自洽場對半柔性線圈的二嵌段共聚物的相行為熔化進行了研究；Naveen C.Andrewsl等[6]用構 型偏倚蒙特卡洛(CBMC)和非平衡布朗動力學(NEBD)模擬來研究分析半柔性聚合物的分子動力學．本文主要用蒙特卡洛(MC)對半柔性聚合物進行模擬研究，對于本體系中半柔性聚合物的剛性，我們引入一個剛性系數Kkend，通過剛性系數的引入，結合自洽場理論對半柔性聚合物的分析和推導，利用蒙特卡洛模擬方法對體系進行計算模擬，其中研究和討論了剛性系數對半柔性聚合的回旋半徑(Rg)和末端距(R0)的影響．

2 模擬和理論

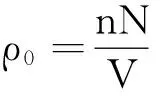
(1)

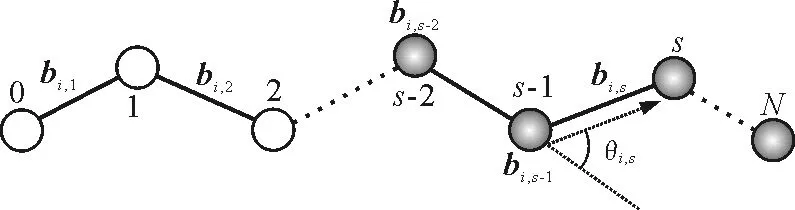
圖1 半柔性高分子模型

其中第i條半柔性AB嵌段聚合物中片段與片段之間的鍵能Hb和非鍵能Hnb為

(2)

(3)

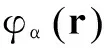
對于半柔性AB聚合物，其聚合物有一定的剛性，為了能引入其存在的剛性能，我們一個剛性系數Kbend，如圖1所示，第s片段在第s-2片段到s-1片段方向上有一定的回復力，對這種回復的強度就用剛性系數Kbend來表示，則其單鏈中所包含的彈性勢能為Hrb

(4)

其中θi,s表示第i條鏈中第s-1個片段到第s個片段的方向矢量與第s-2個片段到第s-1個片段的方向矢量的夾角．

則對于半柔性AB聚合物鏈，其體系的Hamiltonian量可以表示為

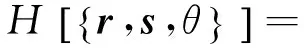
(5)

通過對體系中各對應的參量進行定義和確定，基本上已經完成了體系Hamiltonian量，但在進行蒙特卡洛計算模擬中，考慮到片段之的鍵長存在一定的伸縮性，則在計算模擬中把鍵長取在0.8～1.2之間模擬．

3 模擬結果和討論

3.1 剛性系數Kbend對回旋半徑(Rg)和末端距(R0)的影響

對于半柔性AB聚合物，A組分與B組分存在排斥勢ζABN=30，不可壓縮勢κp=50，其中A組分占總片段數的比例為0.5，分別對不同聚合物數在不同剛性系數下得回旋半徑和末端距進行研究．

(1)在稀溶液體系中，其中忽略溶劑對半柔性AB聚合物體系的影響，通過研究模擬發現，如圖2所示，隨著剛性系數的增強，其回旋半徑(Rg)和末端距(R0)也在不斷的增長，則說明在稀溶液中剛性系數對半柔性聚合物的回旋半徑和末端距有很大的影響，且顯線性增長．

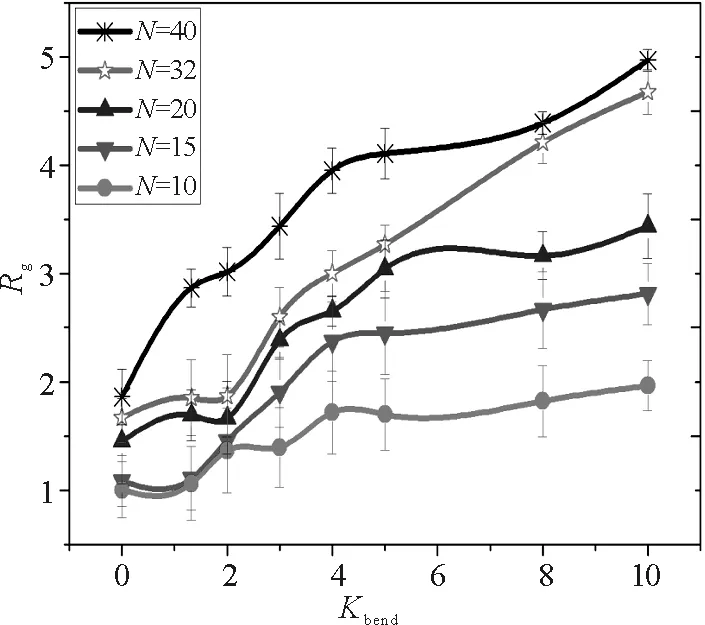
圖2 回旋半徑Rg和末端距R0隨剛性系數Kbend的變化情況

(2)在高濃度體系中，通過對半柔性聚合物回旋半徑和末端距的研究發現，如圖3所示，通過研究發現，對于同一剛性系數的半柔性聚合物鏈，隨著聚合度的增加其回旋半徑和末端距在增加，但對于同一聚合度的聚合物其回旋半徑和末端距不受剛性系數的影響，則說明在高濃度體系中，半柔性聚合物片段之間的相互作用勢要大于分子本身的剛性作用勢．

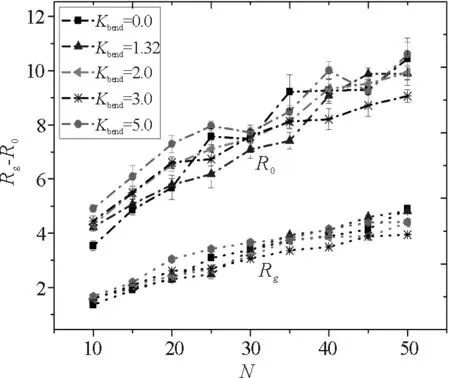
圖3 不同聚合度下回旋半Rg和末端距R0隨剛性系數Kbend的變化情況

3.2 剛性系數Kbend對余輝長度(LS)的影響

對于半柔性聚合物分子，通過上述的研究和模擬不能發現其末端距和回旋半徑的差異，則為了更好地研究和反應剛性聚合物分子的特點，我們引入投影長度(Ls)來研究剛性聚合物分子的特性，則對于一條聚合物分子的平均余輝長度可以表示為

(6)

其中θi,s為第i條鏈上的第i-2個片段到第i-1個片段的矢量與第i-1個片段到第i個片段矢量的夾角如圖1所示．

根據上式模擬發現，對于同一條聚合物，當剛性系數Kbend不斷加強時，其余輝長度也在不斷的增加，且余輝長度與單條聚合物的聚合度(N)成正比，如圖4所示．

即

LS∝a*N

(7)

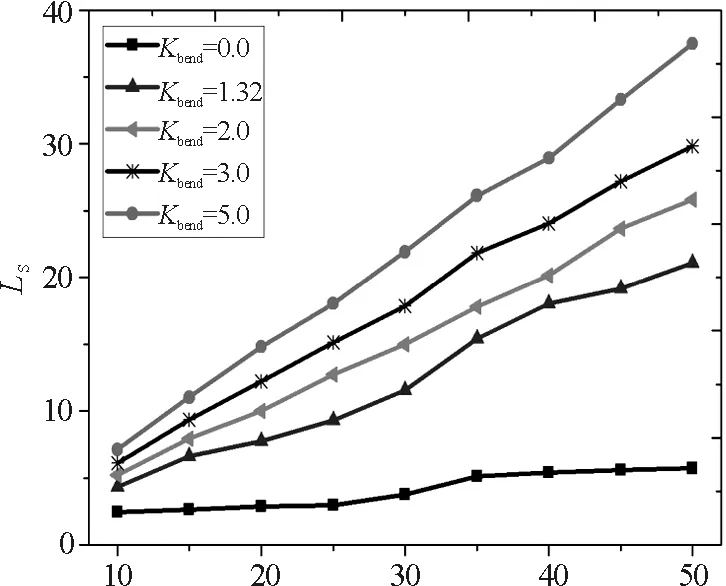
圖4 不同剛性系數Kbend下，余輝長度 (LS)隨聚合度(N)的影響

同時為了研究余輝長度與剛性系數Kbend的關系，我們研究了Kbend對余輝長度的影響，通過研究發現，對聚合物體系剛性系數Kbend對余輝長度的影響也存在一定的影響，如圖5所示．

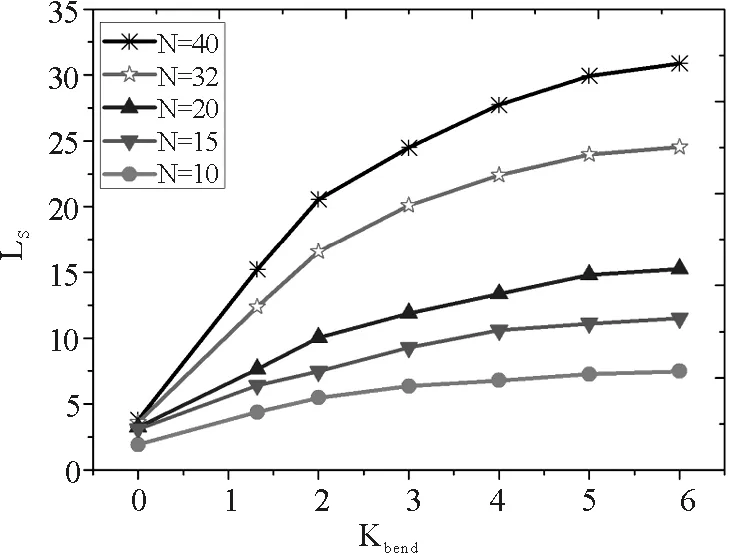
圖5 不同聚合度(N)下，余輝長度(LS) 隨剛性系數Kbend的變化

通過相應的數據處理和模擬計算，發現余輝長度與聚合度(N)的關系系數a=0.4±0.045，余輝長度與剛性系數(Kbend)的關系系數

b=0.4±0.045

即可以表示為

(8)

其中a=0.4±0.045，b=0.4±0.045．

3.3 體系濃度對余輝長度(LS)的影響

為了能充分地了解體系濃度(ρ)對半柔性聚合物的相關性質，我們還研究了體系濃度對與余輝長度的影響，通過研究發現，余輝長度不受體系濃度的影響如圖6所示．

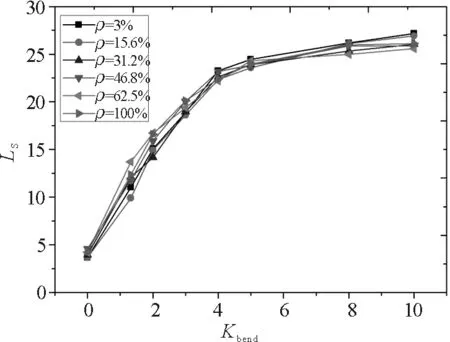
圖6 不同體系濃度(ρ)下，余輝長度(LS) 隨剛性系數Kbend的變化

4 總結與展望

隨著高分子研究的不斷深入，半柔性聚合物的研究也在不斷的提升，對于半柔性聚合物，其結構比一般的柔性高分子要復雜許多，則在研究時要考慮的參數有很多，這樣一來對計算模擬帶來很大的困難．本文中主要以簡單半柔性聚合物為研究對象，對其末端距(R0)、回旋半徑(Rg)、余輝長度(LS)受剛性系數的影響．通過研究發現剛性系數對余輝長度的影響很大，則余輝長度LS可以用來反應半柔性聚合物分子的一個特征．

隨著半柔性研究的深入，我們可以逐步來研究納米粒子復合材料[16～19]、DNA分子、多肽等半柔性高分子的研究，同時可以結合實驗來研究半柔性分子的一些特性，這對高分子的研究有一定的促進作用．

1 Wendi Song,Ping Tang,Hongdong Zhang,et al.New Numerical Implementation of Self-Consistent Field Theory for Semiflexible Polymers.Macromolecules,2009(42):6 300～6 309

2 Wendi Song,Ping Tang,Feng Qiu,et al.Phase behavior of semiflexible-coil diblock copolymers: a hybrid numerical SCFT approach.Soft Matter,2011(7):929～938

3 Jie Gao,Wendi Song,Ping Tang,et al.Self-assembly of semiflexible block copolymers:2D numerical implementation of self-consistent field theory.Soft Matter,2011(7):5 208～5 216

4 Jie Gao,Pi ng Tang,Yuliang Yang.Non-lamellae structures of coil-semifl exible diblock copolymers.Soft Matter,2013(9):69～81

5 Ying Jiang,Jeff Z.Y.Chen.Influence of Chain Rigidity on the Phase Behavior of Wormlike Diblock Copolymers.PRL,2013(110):138 305

6 Naveen C.Andrewsl,Anthony J.MeHugh,Jay D.Schieber.Configuration biased Monte Carlo and Brownian dynamics simulations of semiflexible polymers in extensional flows. Macromol. Theory Simul, 1998(7):19～26

7 肖立勇,曾云蘭,張博凱.摻雜無機性納米粒子的嵌段聚合物體系的場理論模擬研究.科學技術與工程,2014,14(11):1 671～1 815

8 Kostas Ch Daoulas, Victor Rühle,Kurt Kremer. Simulations of nematic homopolymer melts using particle based models with interactions expressed through collective variables.J. Phys.:Condens. Matter,2012(24):284 121

9 C M Chen,Paul G Higgs. Monte-Carlo simulations of polymer crystallization in dilute solution.Journal of ChemicalPhysics, 1998,108(10):4 305～4 314

10 Jianhui Song,Tongfei Shi,Yunqi Li,et al.Rigidity effect on phase behavior of symmetric ABAtriblock copolymers:A Monte Carlo simulation.The Journal Of Chemical Physics,2008(129):054 906

11 Jan Kierfeld,Krzysztof Baczynski,Petra Gutjahr,et al.Modelling semiflexible polymers: shape analysis, buckling instabilities, and force generation.Soft Matter,2010(6):5 764～5 769

12 N Arun Kumar ,Venkat Ganesan.Communication: Self-assembly of semiflexible-flexible block copolymers.The Journal of Chemical Physics, 2012(136):101 101

13 Jan Kierfeld, Krzysztof Baczynski,Petra Gutjahr,et al.Semiflexible Polymers and Filaments: From Variational Problems to Fluctuations.American Institute of Physics,2008:151～182

14 J N Bright,D R M Williams.Collapse of semi-exible brushes in poor solvents:Tilting and bending.Europhys. Lett.1999,48(5):540～546

15 M. Baratlo,H. Fazli.Molecular dynamics simulation of semiflexible polyampholyte brushes-The effect of charged monomers sequence.Eur.Phys.J.E,2009(29):131～138

16 Philip C Nelson.Generalized theory of semiflexible polymers.Physical Review E,2006(73):031 906

17 胡顯奎,林少全,劉振興.聚合物基無機納米粒子復合材料的制備技術及應用展望.材料導報,2000,14(10):62～63

18 王春艷.聚合物/無機納米復合材料的發展及應用.化學工程師,2001(6):21～22

19 Matsen M.W,Schick M.Microphases of a Diblock Copolymer with Conformational Asymmetry.Marocmolecules,1994(27):4 014～4 015

Highlights:The semi-flexible polymer system has been investigated used by the Monte Carlo simulation method based on the Ideological and theoretical of Particle representation to Density field representation in self-consistent field theory. The Hamiltonian of the system include the bond energy, the volume repulsion energy and the bending elastic energy, which can be expressed by the elastic energy, the density of polymer segments, the elasticityKbend, respectively.

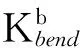
MonteCarloSimulationStudyontheEffectofStiffnessCoefficientKbendontheSysteminSemiFlexiblePolymers

XiaoLiyongJiDenghui

(SchoolofElectricalengineeringofLiupanshuiNormalUniversity,Liupanshui,Guizhou553004)

semi flexible polymer；field representation；projection length；monte carlo simulation

*國家自然科學基金，項目編號：11504078； 貴州省聯合基金重點項目，項目編號：黔科合LH字[2014]7449；六盤水師范學院高層次人才科研啟動基金LPSSYKYJJ201404；貴州省教育廳重點項目，項目編號：黔教合KY字[2015]379號

肖立勇(1986- )，男，碩士，講師，主要從事軟凝聚態物理中的納米粒子粒子復合材料的研究.

紀登輝(1985- )，男，博士，主要從事磁性納米功能材料研究.

2017-03-24)