滑動回歸最小二乘算法在某電動振動臺模型辨識中的應用

嚴 俠，鄧 婷

(中國工程物理研究院總體工程研究所，四川 綿陽 621900)

滑動回歸最小二乘算法在某電動振動臺模型辨識中的應用

嚴 俠，鄧 婷

(中國工程物理研究院總體工程研究所，四川 綿陽 621900)

為了能夠準確地建立電動振動臺的仿真模型，了解電動振動臺系統特性，筆者在分析電動振動臺數學模型的基礎上，利用先進的滑動回歸最小二乘辨識算法，有效地開展了電動振動臺這一復雜電力學系統階數和時延的確認，參數估計，并最終建立了系統的ARMA模型；文章最后，舉出了某型電動臺空臺面和另一型振動臺帶滑臺的模型辨識結果，并通過正弦掃頻試驗給予驗證；結果表明，該算法辨識精度高，收斂速度快，魯棒性強，能克服一定的噪聲，對于高階線性系統辨識具有良好的辨識效果。

電動振動臺，最小二乘， ARMA模型，正弦掃頻振動

0 引言

實驗室開展的振動試驗可用于考核武器系統、航天航空飛行器等機電類產品對振動環境的適應性能力。通過振動試驗可以充分掌握或了解產品的結構和動力學特性，并且評價其在振動環境下的功能可靠性，為產品的設計、改進提供參數和依據。電動振動臺作為振動試驗的主體關鍵設備，以其控制頻帶寬、易于實現等優點得到了廣泛的應用。開展電動振動臺模型分析與辨識研究，一方面能夠對電動振動臺系統的內部結構和工作原理有更進一步的了解，有助于準確掌握其特性與性能。同時，通過建立逼真的電動振動臺仿真模型，還能為開展振動試驗控制技術研究和振動試驗仿真技術研究提供控制和研究對象。

系統辨識工作早在19世紀70年代開始，有許多經典的參數辨識方法已經成功地應用在許多辨識問題上，這些方法包括最小二乘(LG)，廣義最小二乘(GLS)，增廣最小二乘(ELS)，輔助變量法(IV)等〔Ljung and S?derstr?m，1983[1]；1987；S?derstr?m and Stoica,1989[2];Johansson,1993[3]等〕。但在系統遭受有色或相關噪聲時，(LG)將產生有偏估計，對于廣義最小二乘，增廣最小二乘，輔助變量法以及多階的最小二乘法〔MSLS〕〔Hsia,1975[4]〕等，都必須了解一定的噪聲信息，這將給實際工業辨識問題帶來困難。

本文引入了滑動回歸最小二乘辨識算法(Shyh-hong Hwang and Min-Lang Lin,2002〔5〕)。該算法主要利用了一個時間加權的數字濾波器對測得的輸入輸出數據進行前期處理，以削弱系統噪聲對辨識的影響。算法收斂速度快，魯棒性強，在模型階數失配以及采樣周期和時間延遲選取不是很合理的情況下，仍能得到接近真實模型的奈奎斯特曲線,可用于系統的模型階數和延遲的確定，高階系統的降階和線性化處理；同時，在系統遭受有色噪聲時參數辨識也能接近無偏估計。對電動振動臺系統而言，電動振動臺與它的前級功率放大器組成了一個具有非線性和時變因素的復雜電力學系統。同時，設備運行中不可避免地遭受50Hz工頻干擾為主的各種電磁電路干擾。因此，利用滑動回歸最小二乘算法，對該振動臺系統進行降階和線性化處理，建立離散ARMA模型是可行的。

1 電動振動臺系統的模型分析

圖1 電動振動臺三維結構示意圖

電動振動臺三維結構示意圖如圖1所示。電動振動臺主要由動圈(運動部件)、動圈導向裝置、臺體、空氣彈簧以及安裝底座組成。電動振動臺是根據電磁感應原理，由臺體勵磁提供在工作磁隙中的較強磁場，通過給動圈電樞通上交變的電壓及電流而產生運動，通常采用靜壓軸承為動圈振動導向，空氣彈簧用于與地基隔振。電動振動臺是一個很復雜的機電系統，要精確的建立其數學模型是十分困難的，忽略其非線性和時變的因素。電動振動臺的數學模型[6]主要由動力學和電學模型組成。

電動振動臺的動力學模型如圖2所示，首先，電動振動臺通常使用空氣彈簧(剛度為KB)，來保證振動臺體進行垂向振動，同時將振動臺體(質量為MB)的振動與建筑物地面隔離。其次，動圈(電樞組件MT+Mc)和臺體(MB)之間也采用柔性連接方式(比如U形彈簧)，對應彈簧(KS)和阻尼(CS)，最后，將電樞和臺面之間看作是彈性體，在模型中把動圈(Mc)和臺面(MT)當作是用彈簧(KC)和阻尼(Cc)連接起來的兩個分離質量，當安裝有試驗對象(MD)時，還會增加彈簧系統質量。

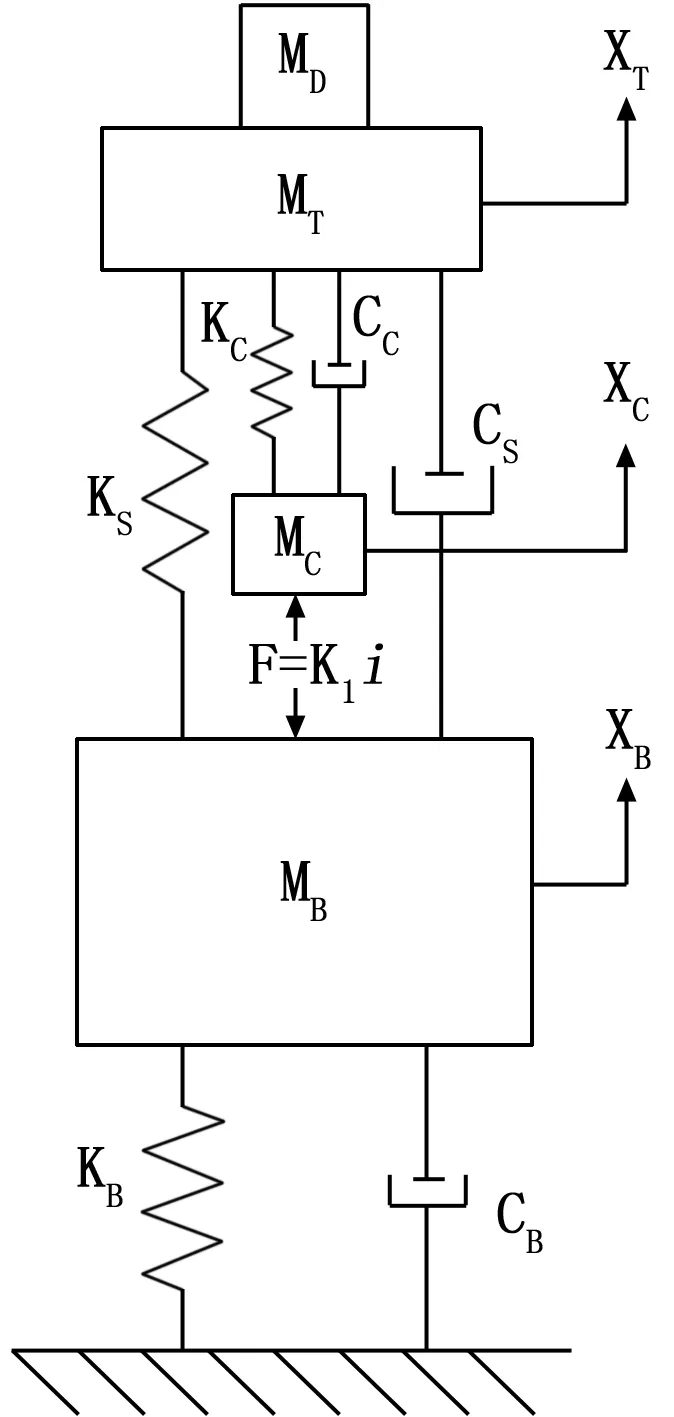
圖2 振動臺的力學模型

振動臺的電學模型如圖3所示，這里必須考慮電樞的電阻和電感。線圈電阻R定義為一個在振動臺輸入端子處(測量)表現出的最小阻抗。這個電阻隨著溫度有所增加，隨著頻率有輕微增加(由于集膚效應)。線圈的電感與鐵磁極件強烈耦合，振動臺振動時引入反生電動勢eback。整個電學回路，由振動臺的前級(功率放大器)提供外部電壓e和電流i來驅動電學回路。

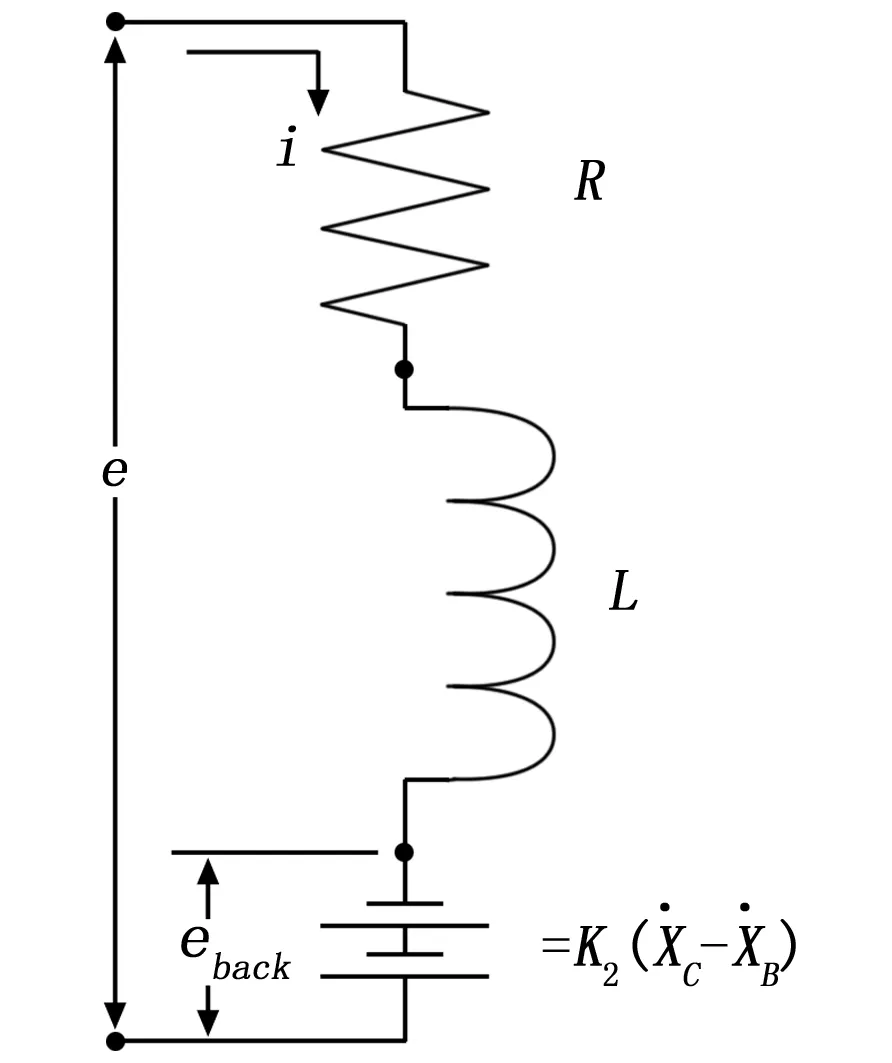
圖3 電動振動臺的電學模型

振動臺的力學部件和電學部件是互相耦合的，機械系統被與電流成比例的力激勵，而電路被與機械速度成比例的內部電壓(反電動勢)所激勵。根據以上關系整個系統的微分方程組表示為：

(1)

系統工作中，由于阻抗受溫度和頻率而變化。同時，振動臺的前級功率放大器作為其驅動也與電動臺的電學模型偶合在一起的，組成了一個復雜的帶有非線性和時變因素的高階系統。在電動振動臺建模過程中，首先忽略阻抗慢變問題，根據式(1)的方程關系，要準確獲得其模型，需要獲得質量、剛度及阻尼的多個參數，實際建模過程中是很難做到的。因此，要準確地建立電動振動臺模型，采用系統辨識的方法將更加有效。

這里，假定功率放大器是線性定常系統，電動振動臺系統可以看成是一個高階線性模型，其ARMA模型如下。

A(z-1)y(k)=B(z-1)u(k)

(2)

這里，

(3)

其中，d表示系統延遲，n表示系統階數，這里n=m。

2 滑動回歸最小二乘辨識算法

該算法是由黃世宏等人提出的，該算法魯棒性強，在有色或相關噪聲情況下仍能取得滿意的估計結果，同時在針對大噪聲情況下和模型失配情況下，仍能得到接近真實模型的奈奎斯特曲線，獲得良好的辨識效果。

2.1 時間加權數字濾波器

為了減少有色噪聲帶來的辨識偏差，引入一個時間加權的數字濾波器，在[ta,tb]時間區間上處理輸入，輸出數據u(k),y(k)。[ta,tb]時間區間上的時間權函數為，

(4)

這里p為權函數階數。對采集數據f(k)在[ta,tb]區間上，令，

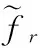
r=0,1,2,…

(5)

則有，

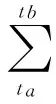
(6)

注意到，當r≤p時

w(ta+i)=0i=0,1,2,…,r-1

w(tb+j)=0j=1,2,…,r

由(6)式可得下式成立，

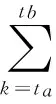
(7)

應用該濾波器，當p≥n，系統的ARMA模型轉化為，

(8)

這里回歸向量ψ和參數向量θ表達如下，

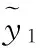
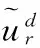
(9)

θ=[a1,…,an,b1,…,bn]T，

(10)

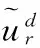
(11)

2.2 滑動回歸最小二乘參數估計法(MRLS)

注意到，式(8)是任意選擇時間間隔[ta,tb]，p≥n。

ta=m-h,tb=m,p=n

式(8)轉化成，

ξ(m)=φ(m)Tθ

(12)

系統離線辨識，要求，h≥n+2，這里m表示當前時刻，

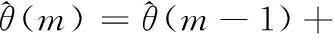
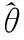
(13)

這里，

μ(m)=1/[1+φ(m)TP(m-1)φ(m)],

P(m)=[I-μ(m)P(m-1)φ(m)φ(m)T]×P(m-1)

2.3 系統的階數和時間延遲的辨識

根據誤差均方求和函數，建立標準。

(14)

3 振動臺模型辨識實例分析

以辨識某型電動振動臺空臺面和另一型電動振動臺帶滑臺的模型為例。辨識中，利用振動控制器產生在給定辨識頻帶范圍內(5～3 000 Hz和5～2 000 Hz)的隨機譜，進行(0.08 g2/Hz)(g是加速度單位，1 g=9.8 m/s2)量值上的隨機振動試驗。同時，采集振動臺系統的輸入，輸出數據，取采樣頻率為10 kHz，整個系統的信噪比在3%左右。此外，再進行相同頻帶范圍內的正弦掃頻振動試驗，來求取其振動臺模型的幅頻特性，并將其與辨識結果比較。

3.1 某型電動振動臺空臺面模型辨識

根據系統辨識數據，運用滑動回歸最小二乘算法，進行該振動臺模型辨識。根據式(14)確定系統的階數和延遲。模型階數和延遲辨識結果如圖4的J函數曲線。

圖4 J函數曲線

從圖4中可以明顯看出，在階數為6和延遲為1處，J函數明顯下降。表明模型的階數和延遲分別近似為6和1，該結果也吻合于所分析的振動臺數學模型。這里我們選取辨識系統的階數分別為6和7，延遲為1，利用該參數估計算法，得出系統的ARMA模型參數分別為，

θ1=[-3.220,5.2960,-5.7752,4.1745,-1.8617,0.4071,

0.2415，0.1140，-0.7687，0.6811，-0.2610，-0.0072]

θ2=[-3.2450,5.3486,-5.816,4.1759,

-1.8130,0.3523,0.0179,0.1864，0.0020，

-0.3812，0.2684，-0.0076，-0.0731，0.0049]

對應模型的幅頻曲線分別如圖5～6。同時6階辨識模型下的參數辨識情況如圖7所示，圖中可以看出，到80步左右參數已經趨于穩定，但有一定慢變，這正是由于電動振動臺具有一定非線性和參數慢變所造成的。此外，對該振動臺空臺面進行了10g下的正弦掃頻試驗，試驗中加速度計的靈敏度系數為100mv/g，所獲得的系統幅頻特性如圖5～8。

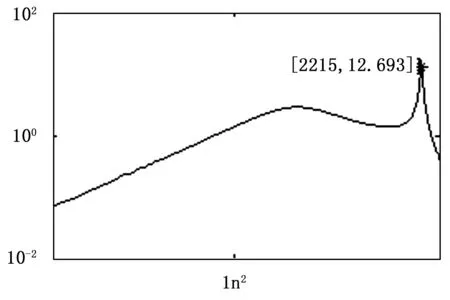
圖5 空臺面6階辨識模型的幅頻曲線

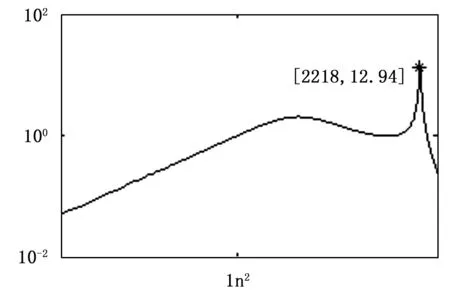
圖6 空臺面7階辨識模型幅頻曲線

圖7 800步內的辨識參數θ1

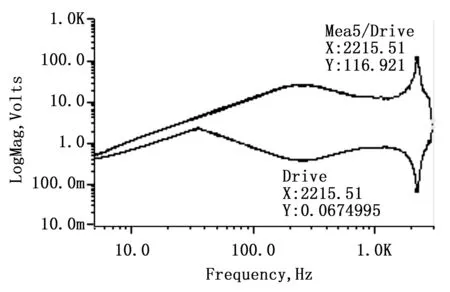
圖8 正弦掃頻下空臺面模型幅頻特性曲線

3.2 另一型電動振動臺帶滑臺模型辨識

根據辨識數據，運用同樣的辨識方法。這里選取系統的階數為13，延遲為1。振動臺帶滑臺的ARMA模型參數辨識結果為，

θ3=[-3.7425,7.0697,-8.9151,8.4603,-6.3591,

3.3625,-0.3656,-1.5232,2.0875,-1.9575,

1.5692,-0.9259,0.2470,0.0552,-0.4437,1.6069,

-3.5384,5.8147,-7.9050,9.4501,-9.7826,

8.1502,-4.9759,1.9137,-0.3180，0.0282]

對應得出模型的幅頻曲線如圖9。此外，在20g下的正弦掃頻試驗所獲得的系統幅頻特性如圖10，這里加速度計的靈敏度系數為10mv/g。

圖9 帶滑臺13階辨識模型的幅頻曲線

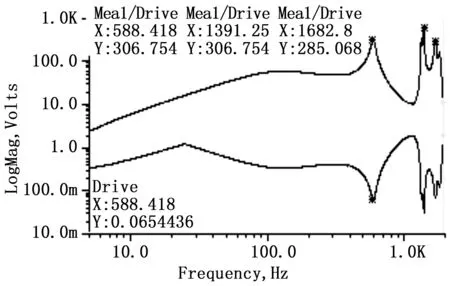
圖10 正弦掃頻下的帶滑臺模型幅頻特性曲線

比較圖5～10，其辨識的模型與真實的模型的幅頻特性很接近，一方面成功地實現了振動臺模型的參數化，另一方面也表明該辨識算法可靠，魯棒性好，辨識精度高，針對高階系統辨識，也能取得較高的精度。

4 結語

本文通過建立電動振動臺的數學模型，運用滑動回歸最小二乘辨識算法，成功地完成了電動振動臺的建模和模型辨識。列舉了電動振動臺兩種狀態下的辨識結果。結果表明，滑動回歸最小二乘算法魯棒性強、辨識精度高，較好地實現了電動振動臺這一復雜高階電力學系統的模型辨識。

[1]LjungL,S?derstr?mT.TheoryandPracticeofRecursiveIdentification[M].MITPress,Cambirdge(1983).

[2]S?derstr?mT,StoicaP.SystemIdentification[M].PrenticeHallInternational,U.K.(1989).

[3]JohanssonR.SystemModelingandIdentification[M].PrenticeHall,EnglewoodCliffs(1993).

[4]HsiaTC.OnMultistageLeast-SquaresApproachtoSystemIdentification[A].ProceedingsofIFACSixthworldCongress[C].Paper18.2,Boston(1975).

[5]Hwangshyhhong,LinMinlang.Amethodforidentificationofdiscreteparametricmodelwithunknownordersanddelays[J].ChinInstChemEngrs, 2002,33(4):373-388.

[6]Georgefoxlang,DaveSnyder.Understandingthephysicsofelectrodynamicshakerperformance[J].SoundandVibration, 2001,35(10):24-33.

Application of Moving-Horizon Recursive Least squares Algorithmin Model Identification for a Electrodynamic Shaker

Yan Xia, Deng Ting

(Institute of System Engineering, China Academy of Engineering Physics, Mianyang 621900,China)

In order to accurately establish the simulation model of electric vibration table, to understand the characteristics of electric shaking table system. Author firstly analyzes the mathematics model of the electrodynamic shaker, and secondly uses the advanced Moving-Horizon recursive least squares algorithm (MRLS) to determine the electrodynamic shaker system order and time delay and estimate the parameters of the system. Finally the ARAM model of the electrodynamic shaker is built. In this paper end, the identification result of a electrodynamic shaker with empty table and another electrodynamic shaker with slip table is given and is verified by making sine sweep vibration tests. The result shows that MRLS algorithm has a good identification capability and strong robustness for the high order line system.

electrodynamic shaker; least-squares estimation; ARMA model; sine sweep vibration

2016-12-06；

2017-02-21。

嚴 俠(1977-)，男，四川成都人，碩士，高級工程師，主要從事振動控制與振動試驗裝備研發方向的研究。

1671-4598(2017)07-0202-04

10.16526/j.cnki.11-4762/tp.2017.07.050

TP216

A