航天器大型柔性附件地面模態(tài)試驗與性能評價研究

臧 旭，唐國安，郭其威，董尋虎

航天器大型柔性附件地面模態(tài)試驗與性能評價研究

臧 旭1，2，唐國安1，郭其威2，董尋虎2

（1?復旦大學航空航天系，上海200433；2．上海宇航系統(tǒng)研究所，上海201109）

航天器大型柔性附件地面模態(tài)試驗既須考慮空氣阻力影響，又要分析地面重力帶來的邊界效應的影響，以動力學特性完全確定的標準桿結構為依托，首先在氣動?電磁懸掛系統(tǒng)上進行不同長度標準桿地面模態(tài)試驗，然后利用Rayleigh?Rize法和有限元法進行數(shù)值仿真模擬，研究表明氣動?電磁超低頻懸掛系統(tǒng)使水平方向測試結果偏高而使垂直方向測試結果偏低，并開展氣動?電磁超低頻懸掛系統(tǒng)性能評價研究，建議通過電磁力抵消附加質量影響并在水平方向增加隨動設計。

氣動?電磁懸掛裝置；零重力模擬；模態(tài)試驗；數(shù)值模擬

1 引言

太陽電池翼、天線、機械臂等航天器大型柔性附件具有低頻、密模、非線性等結構動力學特性，需通過地面動力學驗證試驗保證其在執(zhí)行任務時的安全性。由于重力、空氣等環(huán)境因素的影響，要在地面上對大型柔性附件進行模擬太空試驗極其困難。目前模擬地面低重力方法主要包括：慣性補償法［1?3］、氣浮法［4］和懸吊法［5］等。慣性補償法僅能得到短時間的零重力環(huán)境；氣浮法由于氣浮組件附加質量及氣浮阻力影響，測試數(shù)據(jù)遠低于在軌數(shù)據(jù)；而懸吊法因其具有附加質量小、試驗時間不受限制且可模擬三維空間的低重力環(huán)境等優(yōu)勢而被廣泛應用。

采用懸吊法模擬低重力環(huán)境，受系統(tǒng)懸掛頻率、附加質量及單擺效應影響，地面動力學測試數(shù)據(jù)與在軌狀態(tài)存在差異。Bertran［6］采用低剛度彈簧系統(tǒng)和橡皮繩懸掛系統(tǒng)，對阿里安4整流罩進行動力學測試。Sleight等［7?8］通過繩索機構及滑輪組，并利用配重抵消太陽帆重力進行模態(tài)測試，綜合考慮懸掛系統(tǒng)及重力影響修正有限元建模，獲取太陽帆在軌動力學參數(shù)。王澤宇等［9］開展了氣浮和懸吊兩種狀態(tài)下的衛(wèi)星微振動對比研究試驗，分析了兩種邊界條件對試驗結果的影響。按GJB2706A—2008《航天器模態(tài)試驗方法》要求，采用懸吊法模擬失重狀態(tài)，要求懸掛系統(tǒng)的固有頻率小于試驗件基頻的1／5，如空間站大面積太陽柔性電池翼基頻約0? 05 Hz，故進行超低頻模態(tài)試驗要求懸掛頻率小于0? 01 Hz，常規(guī)低剛度彈簧系統(tǒng)和橡皮繩懸掛系統(tǒng)無法滿足需求。

氣動?電磁超低頻懸掛裝置可模擬在軌零重力和無摩擦環(huán)境，該系統(tǒng)懸掛頻率小于0? 03 Hz，已成功運用于剛性、半剛性太陽電池翼等低頻（基頻0? 1 Hz～0? 2 Hz）附件地面模態(tài)試驗［10］。當超低頻柔性附件基頻為0? 05 Hz左右時，系統(tǒng)懸掛頻率、附加質量及單擺效應影響不可忽略，需要根據(jù)氣動?電磁懸掛裝置動力學特性，修正試驗數(shù)據(jù)獲取柔性附件動力學參數(shù)。

本文以動力學特性完全確定的標準桿為對象，采用氣動?電磁裝置懸掛模擬自由邊界條件，使用預緊力釋放和大位移激振器激勵2種激勵方法對其進行測試，將氣動?電磁懸掛裝置＋標準桿系統(tǒng)簡化為帶有任意分布彈簧質量系統(tǒng)的梁的自由振動問題，運用Rayleigh?Ritz法［11］和有限元法研究氣動?電磁超低頻懸掛系統(tǒng)對航天器大型柔性附件地面模態(tài)試驗結果的影響，并開展氣動?電磁超低頻懸掛系統(tǒng)性能評價研究，給出該系統(tǒng)的適用范圍及改進方案。

2 地面模態(tài)試驗方案設計

2? 1 標準桿試驗件

采用一套動力學特性完全確定的標準桿模擬航天器大型柔性附件。標準桿件由若干根長2 m的鋁管通過質量為1? 3 kg的法蘭盤連接而成，每節(jié)連接處可以安裝配重塊，鋁管截面為空心梁，內外徑分別為0? 07 m和0? 065 m，每兩根鋁管之間的法蘭盤通過8個螺栓連接在一起，以保證連接剛度，如圖1所示。試驗前通過調節(jié)標準桿節(jié)數(shù)及增加質量為2 kg的配重塊設計標準桿一階頻率。

2? 2 自由邊界條件的模擬

航天器大型柔性附件模態(tài)試驗所面臨的首要問題是自由邊界條件的模擬，本文采用氣動?電磁超低頻懸掛系統(tǒng)，如圖2所示，主要由氣動子系統(tǒng)和電磁子系統(tǒng)構成。其中：氣動子系統(tǒng)主要由無摩擦氣缸?活塞、外部儲氣罐、精密氣壓控制裝置等構成，除了給試驗系統(tǒng)提供無摩擦的環(huán)境條件外，還須提供恒定的懸掛力以平衡試件的重力；電磁子系統(tǒng)由長行程動圈作動器和配套的功率放大器、位移傳感器、加速度傳感器、高精度壓力傳感器以及壓力波動計算機處理電路、計算機控制裝置等構成，并且須提供非接觸的電磁力以滿足懸掛裝置對微小力的各種需求［12］。試驗中試件呈水平展開，每個吊點處采用直徑1 mm的鋼絲繩吊掛在氣動?電磁懸掛裝置上，通過調節(jié)氣缸氣壓來平衡試件的重力，試件根部通過轉接工裝直接安裝固定在模態(tài)試驗工裝上，試件底部用可調節(jié)支架支撐，主要起保護作用，試驗時須與試件分離，如圖3所示。

2? 3 激勵點的選取

選擇激勵點位置，最常用的方法是以對驅動點留數(shù)的研究為基礎的。留數(shù)Aijr借助模態(tài)參數(shù)由式（1）的頻響函數(shù)表達式定義：

在純模態(tài)情況下，若按單位模態(tài)質量換算，模態(tài)比例系數(shù)則如式（2）：

因此，驅動點留數(shù)（i＝j）如式（3）：

（1）、（2）、（3）式中，ψir、ψ?ir為復值模態(tài)位移，λr、λ?

r為共軛極點。由（3）式可知，某個或某些自由度對于盡可能多的模態(tài)，當留數(shù)值Aijr較大時，這樣的自由度就是比較好的激勵點，當某個ψir為零時，意味著激勵點在某一階模態(tài)的一個節(jié)點上，將會導致這階模態(tài)不能檢測出來［13］。試驗中在式（3）的理論支撐下，結合工程經驗及需求選擇單點激勵點的位置，并根據(jù)預試驗結果調整。2? 4 激勵方式

由于試件一階頻率很低，用肉眼就可以看到其擺動的振型，且無任何附加干擾因素的影響，對此類低頻柔性結構來說，預緊力釋放自由衰減法是最直觀、最可靠的方法。試驗采用預緊力釋放自由衰減法和大位移激振器激勵法相互校驗獲取試件頻率和振型測試數(shù)據(jù)。

2? 5 傳感器選取及測點布置

柔性附件自身基頻較低，采用接觸式傳感器將引入附加質量降低系統(tǒng)頻率、增加測試難度，故采用激光位移傳感器。傳感器的數(shù)目和位置取決于關心頻率范圍、期望的模態(tài)數(shù)目、試件上的關心區(qū)域、可用的傳感器數(shù)。結合仿真分析和預試驗確定傳感器位置和個數(shù)，測點的數(shù)量和位置應表征在工程有意義頻帶內各階主模態(tài)振型的基本輪廓［13］。對于標準桿試驗，在每個法蘭盤連接處設置一個傳感器。

3 試驗實施

模態(tài)試驗先采用預緊力釋放法測試，記錄試驗時域和頻域數(shù)據(jù)，根據(jù)測試數(shù)據(jù)初步得到試件基頻，再進行激振器激勵試驗。試驗采用單點隨機激勵方式，頻率分辨率設定為0? 01 Hz。為了防止功率泄漏，采用漢寧窗方式進行加窗處理。模態(tài)試驗采用LMS系統(tǒng)進行數(shù)據(jù)采集和處理，試驗結果按GJB2706A?2008《航天器模態(tài)試驗方法》對所有試驗數(shù)據(jù)品質進行評定，通過相干性、互易性、數(shù)據(jù)重復性以及模態(tài)特性的相關性檢查與檢驗對試驗所測得的結果進行判定，從而識別出試件真實的各階模態(tài)參數(shù)。表1為11個工況模態(tài)試驗狀態(tài)及測試結果。

4 氣動?電磁懸掛裝置影響分析

4? 1 氣動?電磁懸掛裝置力學等效

采用懸吊法模擬低重力環(huán)境，會改變被測系統(tǒng)的邊界條件，需要根據(jù)懸掛裝置設計原理獲取其動力學特性，分析該裝置帶來的邊界條件效應對被測系統(tǒng)動特性的影響。氣動?電磁懸掛裝置在與地面垂直方向能提供恒定的平衡試件重力的懸掛力Td，并沿垂直地面方向無摩擦隨動，即提供超低懸掛頻率，可將其簡化成一個彈簧質量系統(tǒng)，懸掛力Td由氣動力Fp和電磁力Fm兩部分組成，如圖4所示，隨動部件附加質量Mv＝5 kg，垂直方向附加剛度kv隨氣缸氣壓變化而變化，氣缸氣壓越大（單點吊力越大），kv越小［14］。系統(tǒng)在水平方向做類單擺運動，恢復力為F恢復＝Td× sinθ＝Td×（y／Ld）＝（Td／Ld）×y，其中Td、Ld、、y分別為懸掛力、懸掛高度和水平位移。當懸掛高度Ld＞＞y時，水平方向也可視為彈簧質量系統(tǒng)，如圖5所示，等效剛度kh＝Td／Ld。

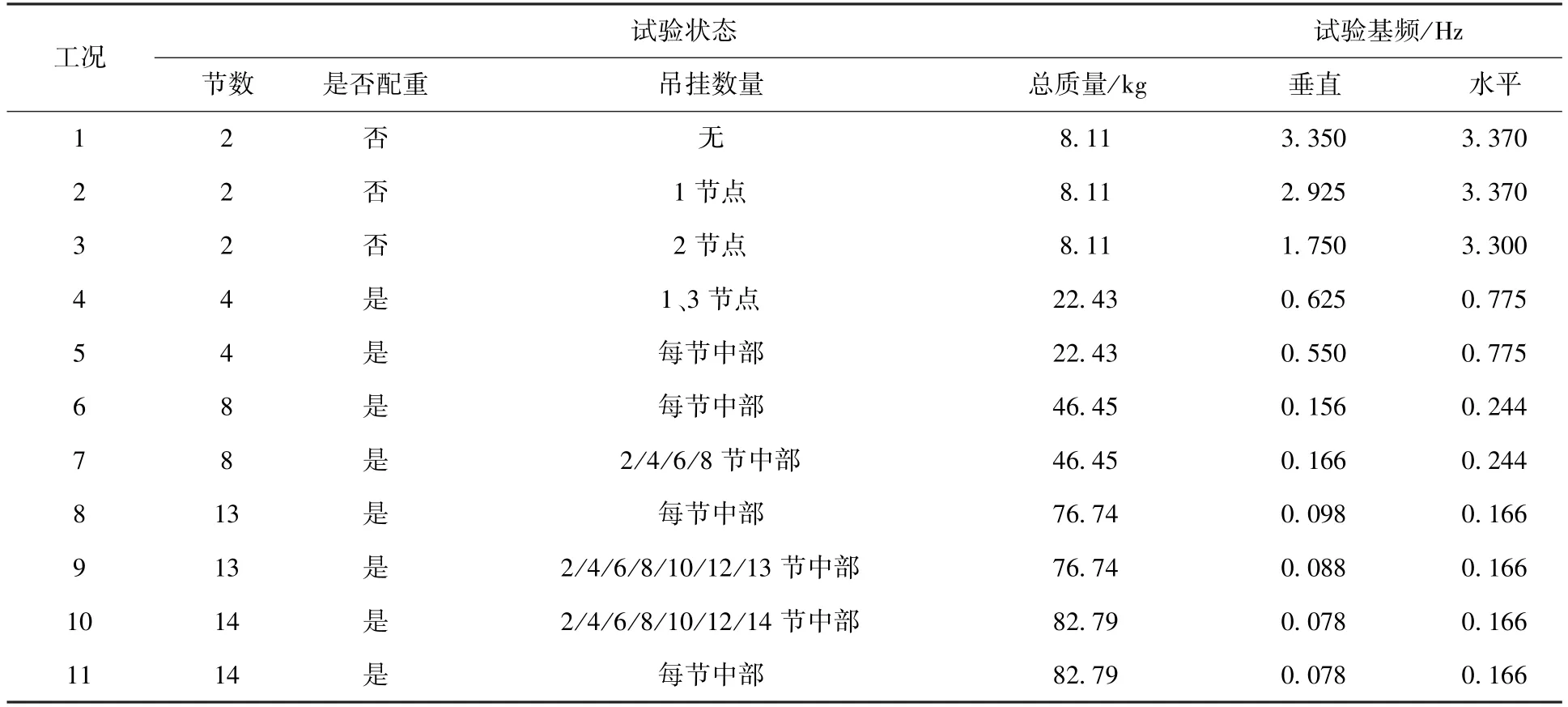
表1 模態(tài)試驗狀態(tài)及測試結果Table 1 Conditions and results of modal test

考慮氣動?電磁懸掛裝置影響的標準桿試件如圖6所示，試件一端固支一端自由，各懸掛點均采用縱向及橫向彈簧模擬。假設標準桿均勻細長，長度為L，截面積為A，密度為ρ，彈性模量為E，截面轉動慣量為I，引入狄拉克δ（x）函數(shù)，集中質量點mi可以考慮為分布質量mi（x）＝miδ（x?xi），其中xi為集中質量點mi所在的位置，對集中彈簧做類似處理，則該模型的彎曲振動方程如式（4）、式（5）所示：

其中，式（4）為垂直方向振動方程，式（5）為水平方向振動方程；i＝1，…，Na，Na為懸掛裝置的組數(shù)，j＝1，…，Nv，Nv為法蘭盤的組數(shù)；wv、wh為梁的垂直和水平方向的振動位移；kv、mv為懸掛裝置的附加剛度和質量，kh為單擺效應的附加剛度，ma為法蘭盤質量。

4? 2 Rayleigh?Ritz法

關于帶有彈簧質量系統(tǒng)梁的動力特性分析，一般運用Rayleigh?Ritz法、傳遞矩陣法或者其他數(shù)值方法進行求解獲得近似結果［15］。本文采用Rayleigh?Ritz法，根據(jù)系統(tǒng)邊界條件令基函數(shù)及梁系振動位移函數(shù)如式（6）、式（7）所示：

將（6）、（7）代入（4），求系統(tǒng)垂直方向特征值ωv

2的問題等價于求泛函式（8）的駐值問題［16］：

即求方程（Kv－Mv）a＝0的特征值問題。求系統(tǒng)水平方向特征值等價于求（Kh－）a＝0的特征值問題，其中：

為了能更好地分析懸掛裝置對梁系的影響，對系統(tǒng)進行簡化處理，假設每兩個法蘭盤之間梁長度相同為l，整個梁系共有n節(jié)，且每個法蘭盤處設置一套懸掛裝置，所有懸掛裝置的吊力相同。令基函數(shù)φk（x）僅取一項，則位移函數(shù)如式（10）所示：

1）垂直方向振動

將式（10）代入式（9）中得到系統(tǒng)沿垂直方向振動基頻如式（11）所示：

并將其與梁系統(tǒng)固有基頻做差得到式（12）：

其中，ωv為垂直方向測試基頻，ω為梁系統(tǒng)固有基頻。當L較小時，系統(tǒng)模態(tài)頻率較高，式（12）第二項大于第一項，此時懸掛裝置附加質量mv起主要作用，測試頻率低于系統(tǒng)模態(tài)頻率；隨著L增加，n→∞，系統(tǒng)固有頻率降低，式（12）第一項逐漸增大，第二項逐漸減小，當?shù)谝豁棿笥诘诙棔r，懸掛裝置附加剛度kv起主要作用，測試頻率高于系統(tǒng)模態(tài)頻率。

2）水平方向振動

與系統(tǒng)垂直方向振動相同，通過基函數(shù)式（9）得到系統(tǒng)水平方向系統(tǒng)基頻如式（13）所示：

其中，Td為單臺懸掛裝置的吊掛力，Ld為其吊掛高度。將k代入h

d

d中得到式（14）：

從式（14）可以得到，由于水平方向等效剛度kh的作用，使得在懸掛裝置下的測試頻率高于系統(tǒng)的固有頻率。隨著L增加n→∞，式（14）分子第一項趨于0，且分母第一項滿足式（15）：

代入式（14）得到，當n→∞時水平方向系統(tǒng)基頻如式（16）：

由式（16）可以看出，水平方向測試頻率高于系統(tǒng)固有頻率，并隨著L增加，n→∞，測試頻率趨近于對應吊高的單擺頻率，即ωh＝

4? 3 有限元法

對考慮氣動?電磁懸掛裝置影響的標準桿試件運用MSC．Patran進行有限元建模，模型如圖7所示。為了考慮懸掛裝置及重力對梁系固有頻率影響，在建模時加入懸掛裝置等效模型。懸掛裝置附加剛度和附加質量分別采用彈簧單元和集中質量單元模擬。彈簧單元上端約束6個自由度，下端與集中質量單元連接處釋放垂直方向自由度，同時施加作用力模擬空氣系統(tǒng)和電磁系統(tǒng)的初始合力，并在邊界條件中加入初始重力場。懸掛裝置的吊繩設置為直徑1 mm的鋼絲繩，吊掛高度11 m。

4? 4 分析結果對比

單臺系統(tǒng)懸掛質量約7 kg，垂直方向附加剛度kv＝2? 3 N／m。為獲得較好的近似解，位移函數(shù)式（6）項數(shù)應比所求固有頻率的階數(shù)多一倍以上，本文選取10項。表2和表3給出n＝4時，系統(tǒng)在垂直和水平方向振動頻率的Rayleigh?Ritz法計算結果與有限元分析結果的對比，其中表2第3列為圖7所示有限元分析結果，第5列為無吊繩狀態(tài)有限元分析結果。對比說明Rayleigh?Ritz法和有限元建模方法的正確性，由于在垂直方向Rayleigh?Ritz法忽略吊繩影響，導致高階頻率與有限元結果偏差較大。表4為標準桿基頻模態(tài)試驗數(shù)據(jù)、Rayleigh?Ritz法計算結果及有限元法分析結果對比，三組數(shù)據(jù)偏差小于5%，進一步說明本文分析方法的有效性。

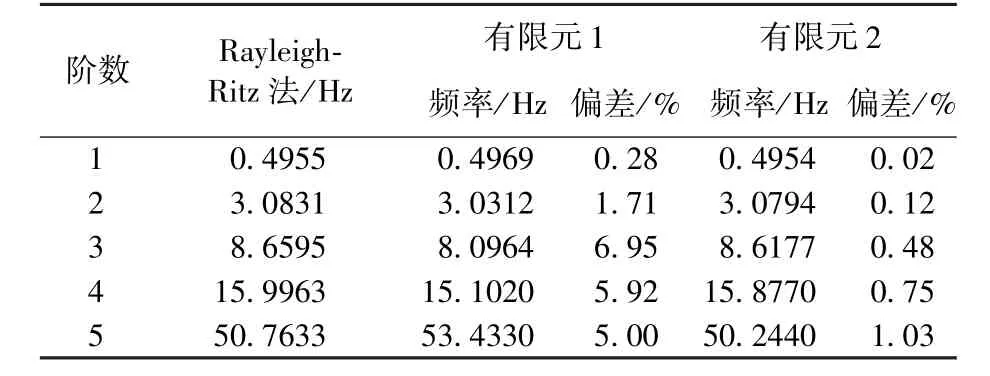
表2 垂直方向前5階固有頻率對比Table 2 Comparison of the first five order inherent fre?quencies in vertical direction

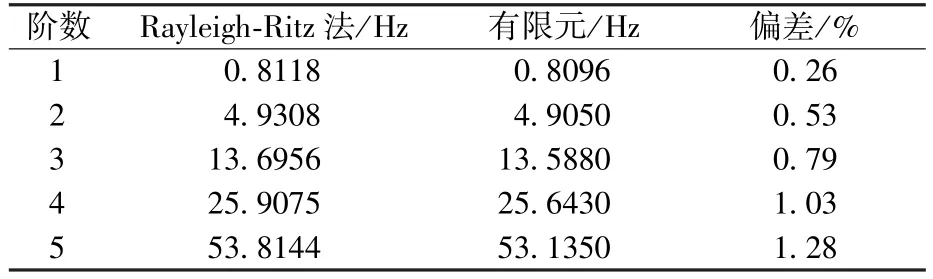
表3 水平方向前5階固有頻率對比Table 3 Comparison of the first five order inherent fre?quencies in horizontal direction

5 氣動?電磁懸掛系統(tǒng)性能評價

氣動?電磁懸掛裝置垂直方向附加剛度kv隨氣缸氣壓變化而變化，且氣缸氣壓越大（對應于試件質量越大），kv越小。同時改變附加剛度kv和梁的節(jié)數(shù)n，系統(tǒng)垂直及水平方向基頻隨節(jié)數(shù)n的變化曲線見圖8和圖9。

在與地面垂直方向受附加質量和附加剛度共同影響，高頻段測試頻率高于真實頻率，隨被測試件頻率下降，測試頻率趨近于真實頻率，并在特定頻率處（附加剛度越低該頻率值越小）超過真實頻率，最終趨向于固定值，測試頻率與真實頻率始終存在誤差。垂直隨動系統(tǒng)附加質量可以通過電磁系統(tǒng)進行抵消［13］，忽略附加質量影響后測試頻率變化曲線如圖10所示。起始段測試頻率與真實頻率保持一致，隨著被測試件頻率下降，測試頻率高于真實頻率，為保證測試值在0? 05 Hz左右且可信，則：1）當kv＜0? 02 N／m時，懸掛裝置系統(tǒng)誤差可忽略；2）當0? 02 N／m＜kv＜1? 2 N／m時，測試頻率變化可辨識，但測試數(shù)據(jù)存在系統(tǒng)誤差需進行理論修正；3）當kv＞1? 2 N／m時，測試頻率變化無法辨識，測試數(shù)據(jù)不可用。

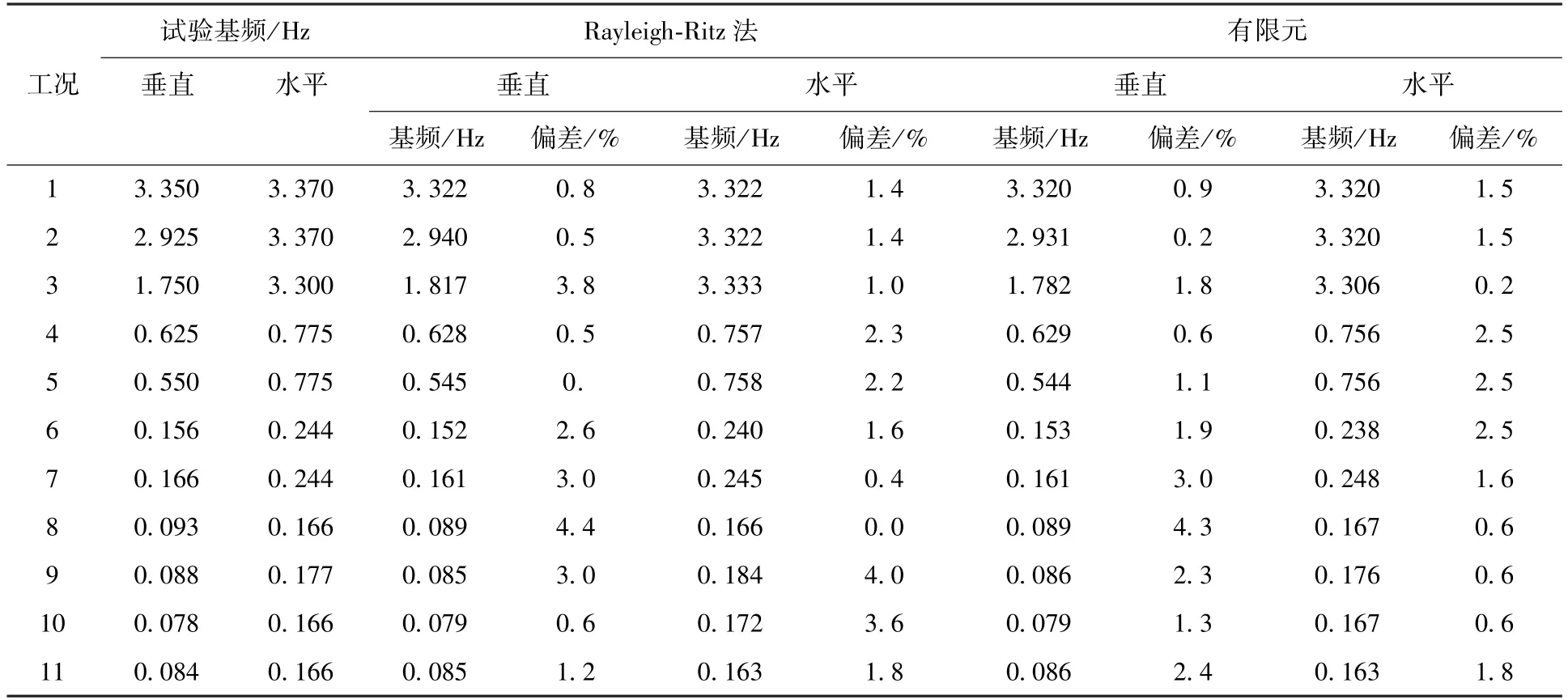
表4 基頻對比結果Table 4 Comparison of the fundamental frequency

在水平方向，當測試頻率高于單擺頻率的4～5倍時單擺效應可以忽略，即被測試件頻率0? 1 Hz需要吊高超過100 m。因此，建議懸掛裝置在水平方向增加隨動設計以消除單擺效應影響。

6 結論

1）對于常規(guī)低剛度彈簧系統(tǒng)及橡皮繩懸掛系統(tǒng)，垂向附加剛度kv無法滿足超低頻柔性附件地面模態(tài)測試要求，但由氣動?電磁懸掛裝置帶來的邊界條件效應對測試結果的影響不可忽略，在模型修正時需考慮懸掛系統(tǒng)及重力因素影響。

2）氣動?電磁懸掛裝置在垂直方向，當被測機構固有頻率較高時，主要表現(xiàn)為附加質量影響，測量頻率低于固有頻率；隨著機構固有頻率降低，附加剛度影響起主要作用，測量頻率高于固有頻率。為了進行超低頻柔性附件（基頻約0?05 Hz）動力學試驗，需要平衡隨動裝置附加質量，并且測試結果對附加剛度kv的取值非常敏感。當kv＜0?02 N／m時，測試數(shù)據(jù)有效，當設計0?02 N／m＜kv＜1?2 N／m時，測試數(shù)據(jù)需進行理論修正，當kv＞1? 2 N／m時，不可在該重力平衡系統(tǒng)上進行測試。

3）氣動?電磁懸掛裝置在水平方向為單擺效應影響，使測試頻率高于系統(tǒng)固有頻率，建議懸掛裝置在水平方向增加隨動設計以消除單擺效應影響。

（References）

［1］ Chen C I，Chen Y T，Wu S C，et al．Experiment and simula?tion in design of the board?level drop testing tower apparatus［J］．Experimental Techniques，2012，36（2）：60?69．

［2］ Nicolau E，Poventud?estrada C M，Arroyo L，et al．Micro?gravity effects on the electrochemical oxidation of ammonia：A parabolic flight experiment［J］．Electrochimica Acta，2012，75：88?93．

［3］ Carignan C R，Akin D L．The reaction stabilization of on?or?bit robots［J］．IEEE Control Systems Magazine，2000，20（6）：19?33．

［4］ Schmitz E．Modeling and control of a planar manipulator with an elastic forearm［C］／／IEEE Int．Conf．Robotics＆Auto?mation，Scottsdale，AZ：IEEE RAS，1989：894?899．

［5］ 劉振．星球車單吊索重力補償與實驗研究［D］．哈爾濱：哈爾濱工業(yè)大學，2013． Liu Zhen．Single?cable Gravity Compensation for Planetary Rovers and Experimental Researches［D］．Harbin：Harbin In?stitute of Technology，2013．（in Chinese）

［6］ Bertran，李慶忠．用擴充的模態(tài)鑒定試驗驗證阿里安4衛(wèi)星有效載荷整流罩數(shù)學模型［J］．國外導彈與航天運載器，1990，（12）：49?58．Bertran，Li Qingzhong．Simulation model of Arian 4 satellite payload fairing with extended modal verification test［J］．For?eign Missiles and Space Carriers，1990，（12）：49?58．（in Chinese）

［7］ Sleight D W，Michii Y，Lichodizieiewski D，et al．Structural a?nalysis of an inflation deployed solar sail with experimental validation［C］／／41th AIAA／ASME／SAE／ASEE Joint Propul?sion Conference＆Exhibit，Tucson，Arizona，2005：78?92．

［8］ Sleight D W，Michii Y，Lichodizieiewski D，et al．Structural a?nalysis and test comparison of a 20＿meter inflation deployed solar sail［C］／／AIAA／ASME／ASCE／AHS／ASC Structures，Structural DynamicsandMaterialConference，Newport，Rhode Island，2006：43?50．

［9］ 王澤宇，鄒元杰，焦安超，等．某遙感衛(wèi)星平臺的微振動試驗研究［J］．航天器環(huán)境工程，2015，32（6）：278?285．Wang Zeyu，Zou Yuanjie，Jiao Anchao，et al．The jitter measurement and analysis for a remote sensing satellite plat?form［J］．Spacecraft Environment Engineering，2015，32（6）：278?285．（in Chinese）

［10］ 劉松，鄒義成，丁瀛，等．大型太陽電池陣模態(tài)試驗方法［J］．航天器環(huán)境工程，2013，30（2）：165?170．Liu Song，Zou Yicheng，Ding Ying，et al．Modal test for large solar array［J］．Spacecraft Environment Engineering，2013，30（2）：165?170．（in Chinese）

［11］ Xu H A，Du J T，Li W L．Vibrations of rectangular plates re?inforced by any number of beams of arbitrary lengths and placement angles［J］．Journal of Sound and Vibration，2010，329：3759?3779．

［12］ Sun Jianhui，Shan Xiaohang，Zhang Xiujun．Analysis and re?search on friction?free cylinder of modal testing suspension system［C］／／WSEAS Transactions on Circuits and Systems et al，Hangzhou，2008：42?46．

［13］ 郭其威，吳松，劉芳，等．航天器模態(tài)分析－試驗體系工程實踐研究［J］．動力學與控制學報，2014，12（3）：274?278．Guo Q W，Wu S，Liu F，et al．Research on engineering practice of modal analysis?test of spacecraft［J］．Journal of Dynamics and Control，2014，12（3）：274?278．（in Chi?nese）

［14］ 孫建輝，王時杰，單曉杭，等．模態(tài)試驗懸掛系統(tǒng)附加質量慣性力抑制效果檢驗技術研究［J］．輕工機械，2010，28（4）：87?90．Sun Jianhui，Wang Shijie，Shan Xiaohang，et al．Research on restraining the attached inertia force in modal test suspen?sion system［J］．Light Industry Machinery，2010，28（4）：87?90．（in Chinese）

［15］ Warburton G B．Response using the Rayleigh?Ritz method［J］．Journal of Earthquake Engineering and Structural Dy?namics，1979，7：327?334．

［16］ 李東旭．高等結構動力學［M］．北京：科學出版社，2010：90?99．Li Dongxu．Dynamics of Structures［M］．Beijing：China Sci?ence Publishing，2010：90?99．（in Chinese）

（責任編輯：龐迎春）

Ground Modal Test and Performance Evaluation of Large Flexible Accessories in Spacecraft

ZANG Xu1，2，TANG Guoan1，GUO Qiwei2，DONG Xunhu2
（1．Department of Aeronautics and Astronautics，F(xiàn)udan University，Shanghai 200433，China；2．Aerospace System Engineering Shanghai，Shanghai 201109，China）

In ground modal test of the large flexible accessories of spacecraft，the impact of air re?sistance should be considered and the impact of the border effect brought by the gravity should be analyzed．Based on the standard beam structure with the determined dynamic characteristics，the ground modal test on beams with different lengths was carried out on the suspension system．Then，the Rayleigh?Rize method and the finite element method were used to conduct the numerical simula?tion．The results showed that the pneumatic?electromagnetic suspension system elevated the horizon?tal test result and decreased the vertical direction test result．In addition，study on the performance evaluation of the suspension system was also carried out．It is recommended that electromagnetic force be used to offset the additional mass effect and the servo design be added in the horizontal di?rection．

pneumatic?electromagnetic suspension system；zero gravity simulation；modal test；nu?merical simulation

V416? 2

A

1674?5825（2017）04?0556?08

2017?03?09；

2017?06?29

上海揚帆計劃（15YF1411900）

臧旭，男，博士研究生，工程師，研究方向為航天器結構動力學。E?mail：zx1063210225＠126．com