變頻正弦混沌神經網絡及其應用?

胡志強 李文靜 喬俊飛

1)(北京工業大學信息學部,北京 100124)

2)(計算智能與智能系統北京市重點實驗室,北京 100124)

變頻正弦混沌神經網絡及其應用?

胡志強1)2)?李文靜1)2)喬俊飛1)2)

1)(北京工業大學信息學部,北京 100124)

2)(計算智能與智能系統北京市重點實驗室,北京 100124)

(2017年1月4日收到;2017年2月7日收到修改稿)

針對暫態混沌神經網絡全局尋優能力受限的問題,提出了一種基于腦電波生物機制的新型混沌神經網絡模型——變頻正弦混沌神經網絡.該模型將變頻正弦函數和Sigmoid函數組合作為非單調激勵函數,本文給出了該混沌神經元的倒分岔圖及Lyapunov指數的時間演化圖,分析了其動力學特性.進一步將該模型應用到非線性函數優化和組合優化問題上,并分析了參數的變化規律.仿真實驗證明變頻正弦混沌神經網絡比暫態混沌神經網絡及其他相關模型具有更好的全局尋優能力.

混沌神經網絡,腦電圖,變頻正弦混沌神經網絡,組合優化

1 引 言

Hopfield神經網絡(Hopfield neural network,HNN)已被證明是解決優化問題的有力工具［1].HNN采用梯度下降法進行尋優,極易陷入局部極小點或出現不可行解［2].Aihara等［3]在HNN結構的基礎上引入負的自反饋,使其表現出混沌行為,提出混沌神經網絡(chaotic neural network,CNN),利用混沌遍歷性、偽隨機性的特性實現不重復的全局搜索.但由于網絡參數固定,導致網絡無法穩定,文獻[4]在Aihara等［3]研究的基礎上引入混沌模擬退火機制,使網絡的混沌行為呈指數衰減形式,最后退化為HNN,提出了暫態混沌神經網絡(transiently chaotic neural network,TCNN),既利用了混沌的全局搜索能力,又使網絡最終得以穩定.

TCNN采用的激勵函數是單調遞增的Sigmoid函數,Shuai等［5]指出有效的激勵函數可取各種形狀,應表現出非單調行為,并提出了奇對稱激勵函數的模型.Potapov和Ali［6]指出激勵函數采用非單調的函數可以使神經元更容易產生混沌動力學特性.基于以上理論,許多學者提出了具有非單調激勵函數的CNN.修春波等［7]將Gauss函數與Sigmoid函數加和組成非單調激勵函數,提出了GS-CNN模型;徐耀群和孫明［8]將Shannon小波函數與Sigmoid函數加和組成非單調激勵函數,提出了SSW-CNN模型;Yi等［9]將正弦函數與Sigmoid函數復合作為非單調激勵函數,并加入時變增益,提出了I-TCNN模型;Xu等［10]將逆多二次函數與Sigmoid函數加和組成非單調激勵函數,提出了RBF-CNN模型;Zhang和Xu［11]將Morlet或Mexican Hat小波函數代替Sigmoid函數,提出了MWCNN和MHWCNN模型.

以上學者所提出的具有非單調激勵函數的混沌神經元模型,雖然都在一定程度上提高了CNN的全局搜索性能,但是大都缺乏一定的生物學機制,無法表征出神經元激勵與響應的頻幅關系,不能充分體現出復雜多變腦部活動的非線性動力學特征和具有更加豐富的混沌全局搜索性能.因此,本文基于腦電波由不同頻率的正弦信號疊加而成的生物機制,采用由變頻正弦(frequency conversion sinusoidal,FCS)函數與Sigmoid函數加權和的形式作為混沌神經元的激勵函數,提出了一種新的CNN模型——變頻正弦混沌神經網絡(frequency conversion sinusoidal chaotic neural network,FCSCNN)模型.在對激勵函數非單調化的同時,使其作用機制更加符合真實的生物神經元特性.給出了FCS混沌神經元的倒分岔圖和最大Lyapunov指數的時間演化圖,分析了其動力學特性.將該新型CNN模型應用于非線性函數優化和組合優化問題中進行仿真實驗,結果表明該模型具有較強的克服局部極小的能力.

2 FCS混沌神經元模型

本文基于腦電波由不同頻率正弦信號疊加而成的生物機制,提出了一種FCS混沌神經元模型.在腦電波中可以觀察到有節律和重復的神經振蕩［12].研究表明,根據不同腦部活動對應腦電波的質量和強度,可將腦電波分為α,β,δ,γ和θ波,五種不同腦電波的特點見表1［12?14].

表1 五種不同腦電波的特點Table 1.The characteristics of fi ve di ff erent brain waves.

由表1可知,不同腦電波形代表人腦的不同活動狀態,并且思維越活躍,腦電波的頻率越高,而幅值會越低.Sih和Tang［14]指出反映大腦思維活動的腦電波由不同頻率的正弦信號疊加而成,思維所需的信息由神經元產生不同頻率和幅值的腦電波來體現.根據以上生物機制,定義FCS函數如下:

其中,u為函數自變量,用于表征腦部活動的強弱;A為正弦函數的幅值,A(0)為幅值初值(0≤A(0)≤1);ε為正弦函數的陡度因子,用于表征正弦函數頻率的大小;ε(0)為陡度因子初值(ε(0)＞ 0);a,b均為正值參數.圖1為A(0)=0.2,ε(0)=0.08,a=b=1時的FCS函數圖像.

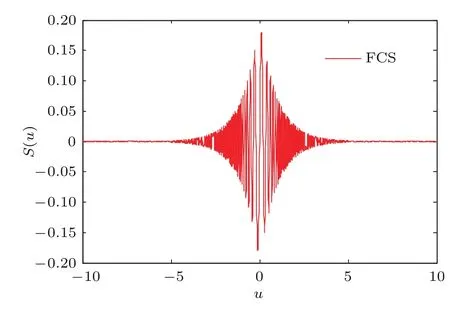
圖1 FCS函數圖像Fig.1.The graph of FCS function.

由圖1可知,構造的FCS函數可以表征腦部活躍度與腦電波的頻率、幅值分別成正比和反比的關系.TCNN的激勵函數為Sigmoid函數,具有普遍的生物學依據,但是并未能體現神經元活躍度的特點.借鑒文獻[5—11]的理論基礎和激勵函數的構造方法,并結合以上生物學機制,將FCS函數與Sigmoid函數加權和作為混沌神經元的激勵函數.將激勵函數非單調化的同時,使之更加符合真實生物神經元的激活抑制以及腦神經不同活躍狀態的特點,提出了一種新的混沌神經元模型——FCS混沌神經元模型,描述如下:

其中,y(t)為神經元內部狀態;x(t)為神經元輸出;k為神經隔膜的阻尼因子(0≤k≤1);ε1和ε2分別為Sigmoid函數S1和FCS函數S2的陡度參數(ε1,ε2＞ 0);c為FCS函數的比例系數(0≤ c≤ 1,c=0時為TCNN模型);I0為正值參數;z(t)為自反饋連接權重(z(t)＞0);β為z(t)的退火衰減因子(0≤ β ≤1).當ε1=0.08,A(0)=0.8,ε2(0)=0.02,a=6,b=1,c=0.25時,S2(u)與f(u)函數圖像如圖2所示.

圖2 (網刊彩色)Sigmoid和Sigmoid+0.25FCS激勵函數曲線對比 (a)FCS函數;(b)Sigmoid+0.25FCS激勵函數Fig.2.(color online)The comparison of activation function between Sigmoid and Sigmoid+0.25FCS:(a)FCS function;(b)Sigmoid+0.25FCS activation function.

圖3 (網刊彩色)a,b對應于幅值和頻率的變化特性 (a)幅值A隨a的變化特性;(b)頻率1/ε隨b的變化特性Fig.3.(color online)The change characteristics of the amplitude and frequency with a,b:(a)The change characteristic of the amplitude A with a;(b)the change characteristic of the frequency 1/ε with b.

由圖2可知,加入FCS后的激勵函數表現出一定的非單調性,同時保持了Sigmoid函數的生物學特性.通過選取不同的A(0),ε2(0),a,b,c值,可以得到不同特點的非單調激勵函數.ε2(0)越小,則正弦函數頻率越高;A(0)和c越大,則FCS函數的權重越大,這都將使得激勵函數非單調程度越大.固定其他參數不變,幅值A和頻率1/ε分別隨a,b的變化特性見圖3.

由圖3可知,a,b分別決定著幅值變化的寬度和頻率變化的陡度,a越大,幅值寬度越小,b越大,頻率陡度越明顯.由(7)式可知,ε2(0),b,u共同決定FCS波函數的頻率(f=1/2πε),其中b,ε2(0)分別控制頻段上下界值,FCS函數的頻段關系見表2.

由表2可知,FCS波頻段和范圍(0.497—100.311 Hz)與表1所列的腦電波頻段和范圍(0.5—100 Hz)一致,符合腦電波頻率的生物機制,其中0.0044≤ ε2(0)≤ 0.32,0.56≤ b≤ 1.8,|u|≤1.神經元的動力學特性可以根據倒分岔圖和最大Lyapunov指數來觀察和體現.正的Lyapunov指數表示模型具有混沌行為,Lyapunov指數越大,表示混沌程度越高［7].Lyapunov指數定義如下:

由(8)—(11)式可得FCS混沌神經元模型的Lyapunov指數計算公式.為了分析比較提出的FCS混沌神經元模型的動力學特性,選取適當的參數,神經元將會表現出暫態混沌的特性.選取參數k=1,β =0.005,ε1=0.02,I0=0.65,z(0)=0.8,A(0)=0.8,ε2(0)=0.04,a=b=1,c=0.25時,FCS混沌神經元與標準暫態混沌神經元(c=0)的倒分岔圖和Lyapunov指數的時間演化圖分別如圖4和圖5所示.

由圖4和圖5可知,隨著自反饋連接權重z(t)的衰減,網絡均經歷倒分岔過程,由混沌態逐漸向倍周期態退化直至穩定在周期一點(不動點).同樣參數條件下,FCS混沌神經元比暫態混沌神經元表現出更豐富的動力學行為,具有更大更多的正值Lyapunov指數,這些決定了新型混沌神經元模型具備更好的全局尋優能力.

圖4 FCS混沌神經元的倒分岔圖及Lyapunov指數時間演化圖 (a)倒分岔圖;(b)Lyapunov指數圖Fig.4.The reversed bifurcation and Lyapunov exponents of the FCS chaotic neuron:(a)Reversed bifurcation;(b)Lyapunov exponents.

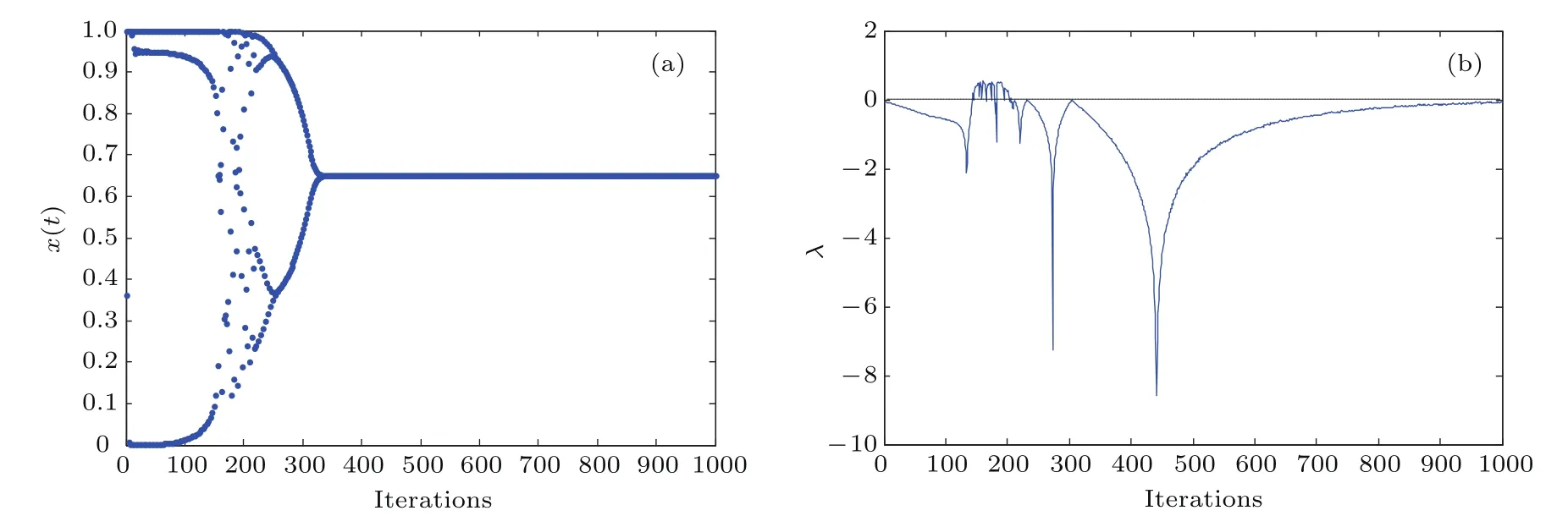
圖5 暫態混沌神經元的倒分岔圖及Lyapunov指數時間演化圖 (a)倒分岔圖;(b)Lyapunov指數圖Fig.5.The reversed bifurcation and Lyapunov exponents of the transient chaotic neuron:(a)Reversed bifurcation;(b)Lyapunov exponents.

3 FCSCNN模型

利用上述FCS混沌神經元模型,構建得到如下FCSCNN模型:

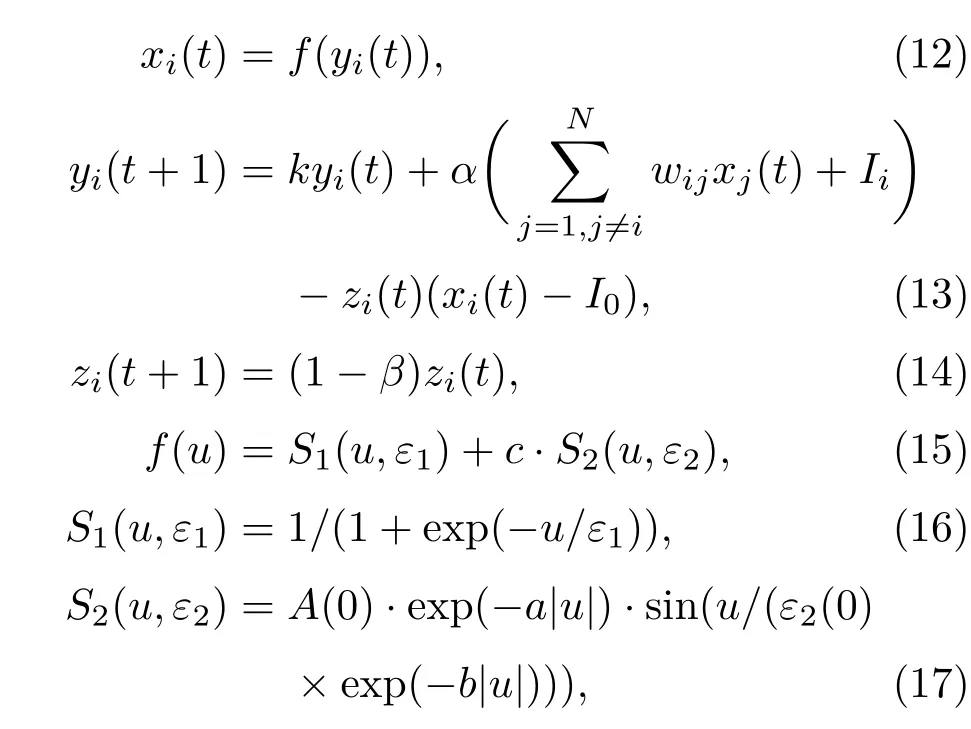
其中,α為輸入正值比例參數,wij為神經元i和神經元j之間的連接權值(wij=wji,wii=0),Ii是神經元i的輸入閾值,其他參數定義同FCS混沌神經元模型.FCSCNN模型結構如圖6所示.

圖6FCSCNN模型結構圖Fig.6.The structure chart of FCSCNN model.

由(12)—(17)式可知,基本網絡參數k,α,β,z(0),I0,ε1及FCS函數參數A(0),ε2(0),a,b,c均有取值范圍,但比較寬泛.參數的選擇對網絡的動力學演化過程及尋優性能有很大影響.選擇合適的模型參數可使網絡處于混沌狀態,并表現出全局搜索能力,使網絡較快地找到最優解.若選取不當,會使網絡無法出現混沌行為,還可能出現不收斂、收斂速度慢、搜索不到最優解、出現不可行解等不良優化效果.實際應用中需要更具體的范圍及選擇方法.由于優化問題復雜性的差異及模型參數間的相互影響和敏感性,目前對于實際優化問題的模型參數選取通常采用試湊法和經驗值.為此,根據現有文獻研究,給出了更為具體的參數選擇方案.k反映記憶或遺忘內部狀態的能力,其值過大會使網絡很快結束混沌態,反之會增加迭代次數,通常設置為經驗值0.9—1［7?10];α反映能量函數對神經動力的影響,使自反饋(混沌)項和梯度項達到某種平衡,其值過大混沌項作用相對較小,降低全局尋優性能,反之能量函數不能充分影響網絡演化,將只在很小范圍內搜索,根據實驗分析及文獻[4,7—11,15—18]仿真實驗,其值設置在0.01—0.5具有較好的優化性能;ε1決定Sigmoid函數的陡度,其值過大網絡收斂快,但準確度下降,反之混沌全局搜索性能強(過于趨近0時反而無混沌行為),其值多設置0.001—0.1［16];對于I0的選擇,目前普遍選擇固定值,常用值為0.56或0.65;β,z(0)分別影響網絡的初始混沌程度和混沌項衰減速度,共同決定網絡的收斂速度,β越大網絡收斂快,但會降低尋優的準確率,而z(0)越大初始混沌運動越劇烈,但網絡收斂慢,對于復雜的中大規模的優化問題通常需要較小的β和較高的z(0).如何權衡準確率和速度的關系,要根據優化問題的復雜度以及實際工程需要設定,并通過參數的設置和自適應方法來實現,這也是該研究方向需要解決的難點之一.

FCSCNN的優化機制同HNN類似,都是將問題的目標函數映射為網絡的能量函數,將網絡的動力學演化過程視為目標函數的尋優過程,當網路收斂到穩定點時,對應的神經元輸出即為所要求得優化問題的(最優/次優)解.根據HNN優化原理有如下規則:

不同的是FCSCNN能量函數E在(19)式表達上有個附加能量項H,H決定著混沌動力的能量值,代表網絡在混沌搜索階段中混沌動力的大小［19].FCSCNN在初始粗搜索階段會利用混沌特性在相空間內按照一定分形結構進行不重復的“自抑制”全局搜索,隨著z(t)的衰減,混沌動力減弱,網絡將經過倒分岔逐步退化到梯度收斂的細搜索階段［15].

其中,H是附加能量項;i=1,2...,N,N為神經元的個數;wij為神經元i和神經元j之間的連接權值;xi為第i個神經元的輸出;Ii是第i個神經元的閾值;τi為第i個神經元的時間常數;f?1(.)為激活函數的反函數.依據(18)式的修改規則可產生多種CNN模型.因此,H的形式決定了HNN能夠具有不同特點的混沌動力行為,進而衍生出不同的CNN模型,進而HNN的能量曲面也就具有了暫態混沌的特點,這也就是TCNN全局優化機制的核心所在.

4 FCS模型在優化問題中的應用

4.1模型在函數優化中的應用

選取以下優化函數:

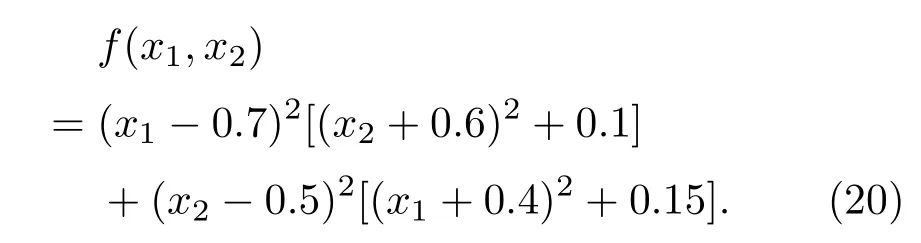
函數f的最小值為0,最小值點為(0.7,0.5);局部極小點為(0.6,0.4),(0.6,0.5)和(0.7,0.4).在FCSCNN模型中,參數選取如下:k=1,α=0.1,β =0.01,ε1=0.05,I0=0.56,z1(0)=z2(0)=0.8,A(0)=0.4,ε2(0)=0.08,a=6,b=1,c=0.25. 隨機初始化x1,x2的值,FCSCNN模型優化函數f的能量函數E的時間演化圖如圖7所示.

圖7 FCSCNN優化函數f的能量函數E的時間演化圖Fig.7.The time evolution diagram of the energy function E for function optimization by FCSCNN.

當網絡迭代800次時優化函數的能量函數值為2.961×10?8,此時,x1=0.69986,x2=0.50006.神經元輸出x1,x2的時間演化圖如圖8所示.

由圖7和圖8可知:FCS神經元輸出值x1,x2(目標解)在前期的尋優方式是具有混沌搜索的遍歷性、偽隨機性的特點,在300步時已經收斂到最優解附近,這種快速、準確的尋優能力很好地證明了FCSCNN的函數優化能力,最優率為100%.為了更好地驗證模型的優化能力,選擇如下復雜的組合優化問題進行實驗分析.

圖8 FCS神經元輸出值x1,x2的時間演化圖 (a)x1;(b)x2Fig.8.The time evolution diagram of FCS neuron output x1,x2:(a)x1;(b)x2.

4.2模型在組合優化中的應用

旅行商問題(traveling salesman problem,TSP)描述如下:假定有個城市,給出它們的位置和相互距離,要求尋找一條閉合路徑,每個城市僅且被訪問一次,回到起始城市,要求這條路徑的距離最短.

問題對應的目標函數［4]為

則由(18)式得,描述求解TSP的FCS神經元內部狀態動力學方程為

其中,xi0=xin,xin+1=xi1,xij為神經元的輸出,它表示城市i于第j個被訪問;W1和W2分別為與約束和關于路徑長度的代價函數對應的耦合系數;dij為城市i和城市j之間的距離.

選取10個城市歸一化后的坐標,取值分別為:(0.4000,0.4439);(0.2439,0.1463);(0.1707,0.2293); (0.2293, 0.7160); (0.5171, 0.9414);(0.8732, 0.6536); (0.6878, 0.5219); (0.8488,0.3609);(0.6683,0.2536);(0.6195,0.2634).已知滿足條件的最短路徑長度為2.6776.在FCSCNN模型中,參數選取如下:k=1,α=0.05,β=0.01,ε1=0.05,I0=0.65,z(0)=0.8,A(0)=0.4,ε2(0)=0.08,a=6,b=1,c=0.25,W1=1,W2=1.隨機初始化xij的值,FCSCNN模型求解TSP時能量函數E和FCS單個神經元x1,1輸出的時間演化圖及最優路徑分別如圖9—圖11所示.

圖9 FCSCNN求解10城市TSP能量函數E時間演化圖Fig.9.The time evolution diagram of the energy function E for 10-city TSP by FCSCNN.

由圖9可知,能量函數的穩定值為1.3388,對應的最短路徑為2.6776,網絡能夠很好地解決TSP.為了更好地分析FCSCNN模型的優化性能,固定參數k=1,α=0.05,β=0.01,ε1=0.05,I0=0.65,z(0)=0.8,W1=1,W2=1,取不同FCS函數參數和模型進行分析試驗.隨機初始化xij的值,進行2000次獨立實驗,每次獨立實驗迭代1000步,結果列于表3和表4.

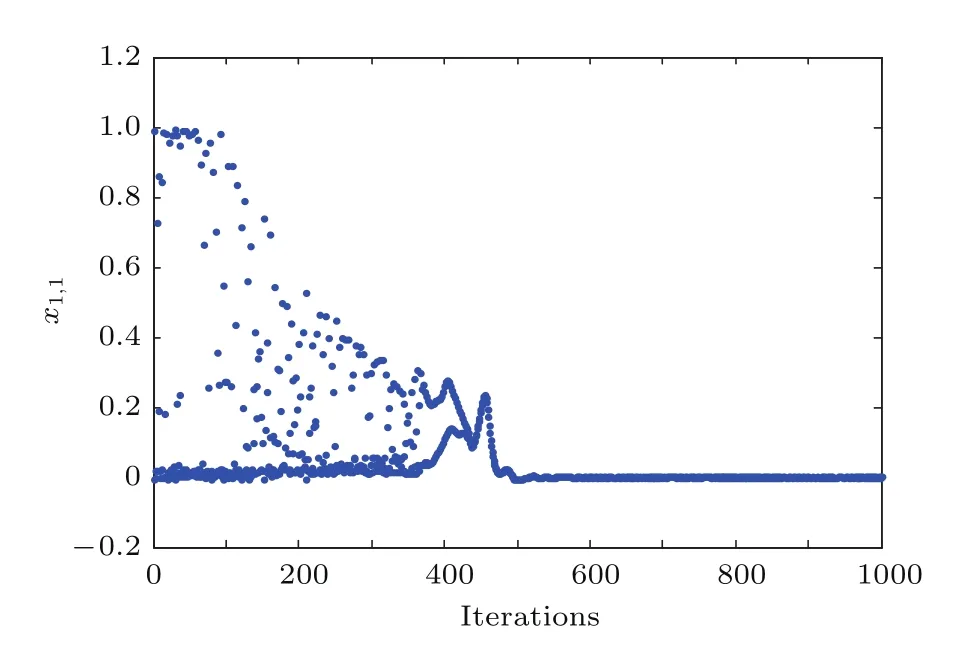
圖10 FCS神經元x1,1輸出的時間演化圖Fig.10.The time evolution diagram of FCS neuron output x1,1.

圖11 10城市TSP歸一化坐標的最短路徑 (a)初始路徑;(b)最優路徑Fig.11.The optimal path in normalization of 10-city TSP:(a)Original route;(b)optimal path.

表3 不同參數下FCSCNN求解10城市TSP結果Table 3.The results of the FCSCNN with di ff erent parameters for 10-city TSP.

表4 不同網絡模型求解10城市TSP問題結果Table 4.The results of the di ff erent models for 10-city TSP.

由表3可知,a值過大或過小(對應于激勵函數的非線性度過小或過大,見圖3)都會使得最優比率下降,其值為6時具有最好的優化性能,而b值的變化對FCSCNN優化性能影響并不明顯,這是由于a對激勵函數的非單調性起到更關鍵的決定作用.當c.A(0)≤0.2時,FCSCNN模型具有較好的優化性能,當c.A(0)＞0.3時,模型的優化能力變差,其原因激勵函數的非線性度過大影響到模型的穩定性,網絡無法搜索到最優解.ε2(0)值越小,優化效果越好,且不會對模型的穩定性產生影響.理論上,只要退火參數足夠小,最終都能夠找到最優解.但是,在相同的演化步數下,對比才能夠體現出不同網絡的全局搜索能力.

由表4可知,提出的FCSCNN模型比其他幾種模型具有更好全局尋優能力.為了進一步檢驗模型對于中大規模問題的尋優能力,選取30和75個城市TSP.已知滿足條件的最短路徑長度如圖12所示,分別為4.237406和5.434474［17].隨機初始化xij的值,選取不同模型進行200次獨立實驗,結果分別如表5和表6所列.

圖12 30和75城市TSP歸一化坐標的最短路徑 (a)30城市;(b)75城市Fig.12.The optimal path in normalization of 30-city and 75-city TSP:(a)30-city;(b)75-city.

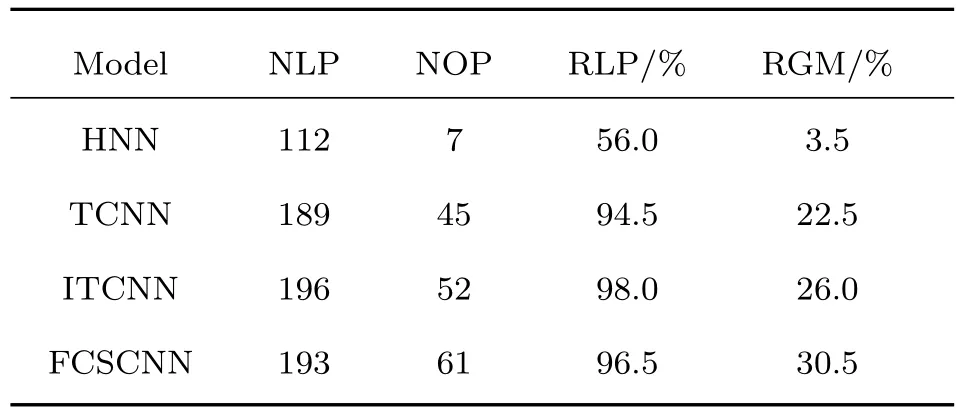
表5 不同網絡模型求解30城市TSP結果Table 5.The results of the di ff erent models for 30-city TSP.

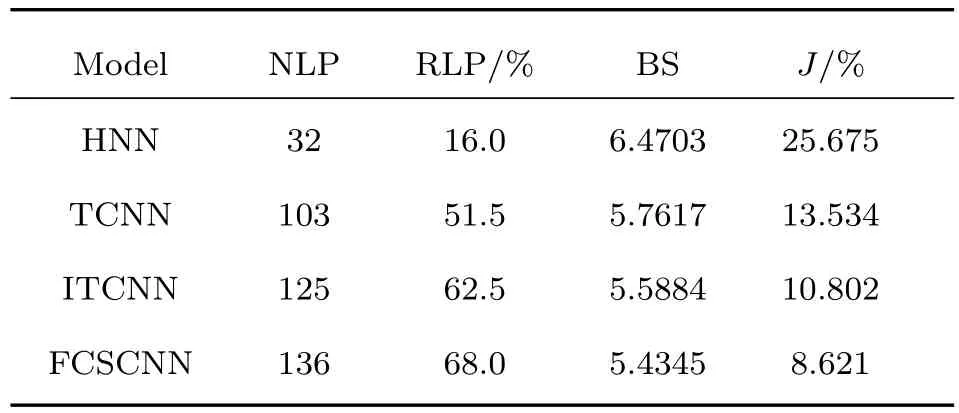
表6 不同網絡模型求解75城市TSP問題結果Table 6.The results of the di ff erent models for 75-city TSP.

由表4和表5可知,最優解比率與城市數(問題的復雜度)成反比.對于75城市的TSP,大多數算法最優率均較低,甚至無法找到最優解(the best solution,BS).因此,引入(23)式所示的評價指數J［18]評估不同模型的優化性能.

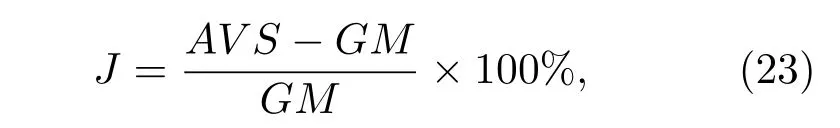
其中,AV S為合法解的均值,GM為全局最優解.J值越低,優化性能越強.

由表4—表6可知,對于不同規模的優化問題,在相同的模型參數條件下,提出的FCSCNN模型比HNN［1],TCNN［4],ITCNN［9]模型具有更高的最優比率和精度,尤其對于能量曲面上具有多個局部極小點的中大規模優化問題,優勢更為顯著.這是由于FCS函數不但增加了神經元激勵函數的非單調程度,并且比傳統的正弦函數具有更豐富的變化特點,這些都奠定了FCSCNN模型具有更好全局尋優性能的動力學基礎.

5 結 論

本文將FCS函數和Sigmoid函數組合作為非單調激勵函數,提出了一種新型CNN模型,即FCSCNN模型,通過繪制該混沌神經元的分岔圖及最大Lyapunov指數時間演化圖可知該新型混沌神經元模型具有暫態混沌動力學特性,并比原模型混沌特性更為明顯,這給混沌搜索提供了更好的全局搜索性能.并且將提出的模型應用到非線性函數優化和組合優化問題上,同時分析了FCS函數參數對模型性能的影響,仿真實驗證明了該模型的有效性和可行性.在參數自適應選擇上還有待改進,也是下一步需要進行的工作.

[1]Han G,Qiao J F,Han H G,Chai W 2014J.Control Decis.29 2085(in Chinese)[韓廣,喬俊飛,韓紅桂,柴偉2014控制與決策29 2085]

[2]Yu S J,Huan R S,Zhang J,Feng D 2014Acta Phys.Sin.63 060701(in Chinese)[于舒娟,宦如松,張昀,馮迪2014物理學報63 060701]

[3]Aihara K,Takabe T,Toyoda M 1990Phys.Lett.A144 333

[4]Chen L N,Aihara K 1995Neural Networks8 6

[5]Shuai J W,Chen Z X,Liu R T,Wu B X 1996Phys.Lett.A221 311

[6]Potapov A,Ali M K 2000Phys.Lett.A277 310

[7]Xiu C B,Liu X D,Zhang Y H,Tang Y Y 2005Acta Electron.Sin.33 868(in Chinese)[修春波,劉向東,張宇河,唐運虞2005電子學報33 868]

[8]Xu Y Q,Sun M 2008Control Theory A25 574(in Chinese)[徐耀群,孫明2008控制理論與應用25 574]

[9]Yi Z,Xu G J,Qin X Z,Jia Z H 2011Proc.Eng.24 479

[10]Xu Y Q,Xu N,Liu L J 2012Appl.Mech.Mater.151 532

從供應來看，原材料價格持續高位，磷礦石供應偏緊，磷酸二銨現貨供應持續緊張。從需求來看，東北、西北地區冬儲剛需較旺，同時出口詢單積極性仍較高。在原料和市場需求支撐下，預計短期內二銨價格高位維穩，后期仍存小幅上漲，重點關注原料價格和冬儲進展情況。

[11]Zhang J H,Xu Y Q 2009Nat.Sci.1 204

[12]Zhang Q H Y,Xie X P,Zhu P,Chen H P,He G G 2014Commun.Nonlinear Sci.19 2793

[13]Zhang X D,Zhu P,Xie X P 2013Acta Phys.Sin.62 210506(in Chinese)[張旭東,朱萍,謝小平,何國光 2013物理學報62 210506]

[14]Sih G C,Tang K K 2012Theor.Appl.Fract.Mec.61 21

[16]Qin K 2010Ph.D.Dissertation(Chengdu:University of Electronic Science and Technology of China)(in Chinese)[秦科2010博士學位論文(成都:電子科技大學)]

[17]Zhao L,Sun M,Cheng J H,Xu Y Q 2009IEEE Trans.Neural Networks20 735

[18]Liu X D,Xiu C B 2007Neurocomputing70 2561

[19]Kwok T,Smith K A 1999IEEE Trans.Neural Networks10 978

PACS:05.45.Gg,07.05.Mh,87.55.deDOI:10.7498/aps.66.090502

Frequency conversion sinusoidal chaotic neural network and its application?

Hu Zhi-Qiang1)2)?Li Wen-Jing1)2)Qiao Jun-Fei1)2)

1)(Faculty of Information Technology,Beijing University of Technology,Beijing 100124,China)
2)(Beijing Key Laboratory of Computational Intelligence and Intelligent System,Beijing 100124,China)

4 January 2017;revised manuscript

7 February 2017)

The optimization performance of transiently chaotic neural network(TCNN)is a ff ected by various factors such as chaotic characteristic,model parameters,and annealing function,and its capacity of global optimization is limited.It is demonstrated that the non-monotonic activation function can generate richer chaotic characteristic than the monotonic activation function in the TCNN model.Besides,the activation function involving neurobiological mechanism can not only re fl ect the rich brain activity in brain waves,but also enhance the non-linear dynamic characteristic,which may further improve the global optimization ability.Hence,a novel chaotic neuron model is proposed with the non-monotonic activation function based on the neurobiological mechanisms from the electroencephalogram.

The electroencephalogram consists of fi ve brain waves(i.e.,α,β,δ,γ,and θ waves)which are de fi ned by the quality and intensity of brain waves with di ff erent frequency bands ranging from 0.5 Hz to 100 Hz.The brain wave with a higher frequency and a lower amplitude represents a more active brain.Researches demonstrate that the fi ve brain waves can be simpli fi ed into sinusoidal waves with di ff erent frequencies.Hence,a frequency conversion sinusoidal(FCS)function which has the consistent frequency range and features with brain waves is designed based on the above neurobiological mechanisms.Then a novel chaotic neuron model with non-monotonic activation function which is composed of the FCS function and sigmoid function,is proposed for richer chaotic dynamic characteristic.The reversed bifurcation and the Lyapunov exponent of the chaotic neuron are given and the dynamic system is analyzed,indicating that the proposed FCS neuron model owns richer chaotic dynamic characteristic than transiently chaotic neuron model due to its special non-monotonic activation function.

Based on the neuron model,a novel transiently-chaotic neural network—frequency conversion sinusoidal chaotic neural network(FCSCNN)is constructed and the basis of model parameter selection is provided as well.To validate the e ff ectiveness of the proposed model,the FCSCNN is applied to nonlinear function optimization and 10-city,30-city,75-city traveling salesman problem.The experimental results show that 1)the FCSCNN has a good performance under the condition of moderate a,smaller c.A(0)and ε2(0);2)on the basis of the appropriate model parameters,the FCSCNN has better global optimization ability and optimization accuracy than Hopfield neural network,TCNN,improved-TCNN due to its richer chaotic characteristic in complicated combinational optimization problem,especially in middle and large scale problem.

chaotic neural network,electroencephalogram,frequency conversion sinusoidal chaotic neural network,combination optimization

10.7498/aps.66.090502

?國家自然科學基金重點項目(批準號:61533002)、國家杰出青年科學基金(批準號:61225016)、國家自然科學基金青年科學基金(批準號:61603009)、中國博士后科學基金(批準號:2015M570910)、朝陽區博士后研究基金(批準號:2015ZZ-6)和北京工業大學基礎研究基金(批準號:002000514315501)資助的課題.

?通信作者.E-mail:zacharyhu33@163.com

*Project supported by the Key Program of the National Natural Science Foundation of China(Grant No.61533002),the National Science Fund for Distinguished Young Scholars of China(Grant No.61225016),the Young Scientists Fund of the National Natural Science Foundation of China(Grant No.61603009),the China Postdoctoral Science Foundation(Grant No.2015M570910),the ChaoYang District Postdoctoral Research Foundation,China(Grant No.2015ZZ-6),and the Basic Research Foundation Project of Beijing University of Technology,China(Grant No.002000514315501).

?Corresponding author.E-mail:zacharyhu33@163.com