基于光束參量優化實現直接驅動靶丸均勻輻照?

李宏勛 張銳 朱娜 田小程 許黨朋 周丹丹 宗兆玉范孟秋 謝亮華 鄭天然 李釗歷

1)(中國工程物理研究院激光聚變研究中心,綿陽 621900)

2)(中國工程物理研究院研究生部,北京 100088)

基于光束參量優化實現直接驅動靶丸均勻輻照?

李宏勛1)2)張銳1)?朱娜1)田小程1)許黨朋1)周丹丹1)宗兆玉1)范孟秋1)謝亮華1)2)鄭天然1)2)李釗歷1)2)

1)(中國工程物理研究院激光聚變研究中心,綿陽 621900)

2)(中國工程物理研究院研究生部,北京 100088)

(2016年12月20日收到;2017年3月7日收到修改稿)

在直接驅動慣性約束聚變中,實現靶丸均勻輻照對靶丸壓縮特性至關重要,通常要求靶丸表面輻照不均勻度小于1%.現有很多優化高功率激光裝置均勻輻照性能的光束排布方案,但受到實際入射光束參量的限制,系統均勻輻照性能難以實現最優化.由于初始輻照不均勻度對靶丸對稱壓縮特性至關重要,為進一步提高靶丸初始輻照的均勻性,并增加系統對打靶過程中由于靶丸直徑變化引起的輻照不均勻的寬容度,從而實現靶丸的中心對稱壓縮,本文對靶丸表面光束的輻照不均勻度進行了數學分析,并研究了不同入射光束參量下的單光束因子項及其對靶丸均勻輻照的影響.結果表明∶對于已知的光束排布結構,存在最優的入射光束參量,使輻照均勻度最高.證明了通過優化入射光束參量提高系統均勻輻照性能的可行性.此外,研究表明單光束因子項與幾何因子項存在一定的匹配關系,可通過分析幾何因子項的特征,求取與之匹配的單光束因子項,進而獲得最優的入射光束參量.本工作為直接驅動靶丸均勻輻照系統的設計和優化提供了一種有效的方法.

∶慣性約束聚變,直接驅動,均勻輻照,入射光束參量

PACS∶52.57.—z,42.79.—e,42.60.JfDOI∶10.7498/aps.66.105202

1 引 言

為實現激光驅動慣性約束核聚變(inertial confinement fusion,ICF),目前有兩種主要的驅動方式,一種是間接驅動[1],采用該驅動方式的高功率激光裝置主要有美國的國家點火裝置(National Ignition Facility,NIF)[2]、法國的兆焦耳激光裝置(Laser Mégajoule,LMJ)[3]和中國的神光-III激光裝置[4]等;另一種驅動方式為直接驅動[5],采用該驅動方式的裝置有歐洲的高功率激光能研究裝置(High Power Laser Energy Research Facility,HiPER)[6]和美國的OMEGA裝置[7]等.相對于間接驅動方式,直接驅動激光能量利用率高,但對于靶丸表面的光束輻照均勻性卻提出了極高的要求,要求靶丸表面輻照不均勻度σrms≤1%[8].因而在直接驅動慣性約束聚變中,提高靶丸表面光束輻照均勻度的技術是近30年以來激光直接驅動方向的研究重點.

在直接驅動中可利用球諧模理論將輻照不均勻度分解,每階輻照不均勻度可表示為相應階數的單光束因子項和幾何因子項的乘積[9].高階輻照不均勻度主要源于單光束內部的高頻起伏及靶丸制作中引入的表面起伏,易導致瑞利-泰勒不穩定[10].高階輻照不均勻度可通過靶丸熱傳導[11]和各種束勻滑技術,如連續相位板(continuous phase plate,CPP)[12]、光譜色散平滑(smoothing by spectral dispersion,SSD)[13]和偏振勻滑(polarizationsmoothing,PS)等[14]技術來進行抑制.低階輻照不均勻度很難通過上述技術來控制,且極易破壞靶丸的壓縮對稱性[15],嚴重時將造成靶丸破裂,聚變失敗.低階輻照不均勻度主要與光束數、光束排布、束間能量平衡、光束指向及入射光束參量(光束模型、束寬、波長)等有關,因而需要尋求特定的光束數、光束排布和入射光束參量來消除低階輻照不均勻度.

為實現直接驅動下的靶丸均勻輻照,CPP,SSD和PS等束勻滑技術已得到廣泛研究;針對光束排布也提出了許多優化方法,如早期提出的對心角錐排布方案[16]、基于理想多面體的排布方案[17]、基于spherical t-design的光束排布方案[18]等.2010年Murakami等[19]提出電子斥力模型方案,可用于任意光束數的光束排布結構優化.2013年,Xu等[20]對電子斥力模型進行了發展,在作用力中引入單光束因子項,提出了粒子梯度力模型優化方法.2015年,Temporal等[21]在LMJ裝置現有框架下研究了對球形靶丸采用20個集束(LMJ的四束光為一個集束)進行直接驅動,來實現沖擊點火初期的靶丸壓縮;模擬了激光能量沉積帶來的沖擊波隨時間的變化,及由此反映的激光驅動不均勻度隨時間的變化;提出了采用兩種不同包絡分布的入射光束相繼輻照靶丸的方法,從而在整個靶丸壓縮過程中降低沖擊波波前的不均勻度,達到動態穩定沖擊波波前的作用.

綜合考慮整個靶丸均勻輻照系統,單光束因子項主要由入射光束參量決定,與光束數、靶場光束排布結構、束間功率平衡等因素無關,對于已知的或已經完成建造的打靶光束排布結構,可以通過優化入射光束參量,使系統輻照均勻度達到最優.從另一個角度而言,在保證輻照不均勻度滿足均勻壓縮的前提下,若將單光束因子項優化至最佳,可降低高功率激光裝置設計和打靶時對幾何因子項的要求,即提高激光裝置實際打靶時對光束指向誤差、束間功率不均衡等因素的容限,從而降低工程難度.

本文通過對輻照不均勻度按球諧模理論進行數學分析,將其分解為單光束因子項和幾何因子項,在此基礎上研究了不同入射光束參量的單光束因子項及其對靶丸輻照均勻性的影響;提出了一種依據光束排布結構,利用幾何因子項特征,對入射光束參量進行優化的方法,并證明了該方法的可行性,為提高直接驅動靶丸輻照均勻性提供了一種有效的方法.

2 理論基礎

按照球諧模理論可將輻照不均勻度進行分解,不均勻度特征波長λ與球諧模階數l的關系為λ=2πR/l,其中R為靶丸半徑.假設各入射光束均為軸對稱分布,且各束光能量相等.如圖1所示,當N束指向球心的光束輻照在球形靶丸上時,第k束光在單位球形表面r處的光束強度為[9]

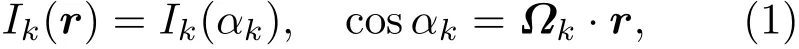
其中,Ik為光束k在靶丸表面的強度分布,αk為光束k的輻照傾角,?k為光束k光軸方向的單位向量.

圖1 光束k的輻照傾角Fig.1.The irradiation angle of laser beam k.

則所有光束在球面r處的光強為

為實現靶丸表面的完全均勻輻照,要求球面上任意一點r處的光強都相等.將Ik(αk)進行勒讓德展開∶

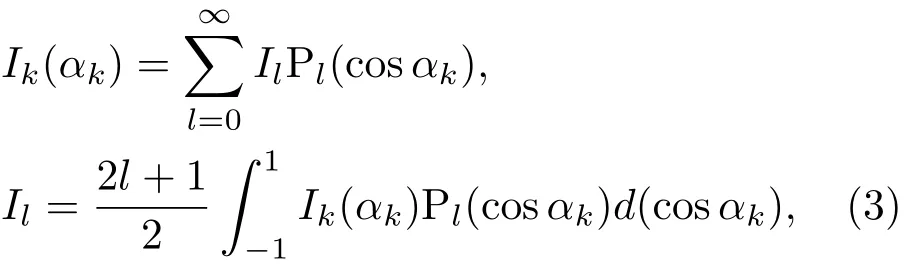
將(3)式代入(2)式中,得

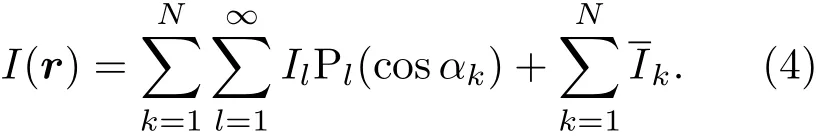
利用勒讓德求和公式

假設每束光在靶丸表面的能量沉積模型相同,此時Il與k無關.將(5)式代入(4)式中,可得

輻照不均勻度為

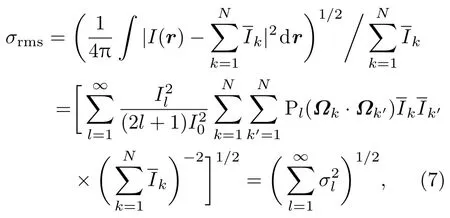
其中σl為l階模的不均勻度

其中Bl為單光束因子項,主要與入射光束參量有關;Gl為幾何因子項,主要與光束數、光束排布、光束指向、束間能量平衡等有關,當各束光之間能量無差異時,幾何因子項可化簡為

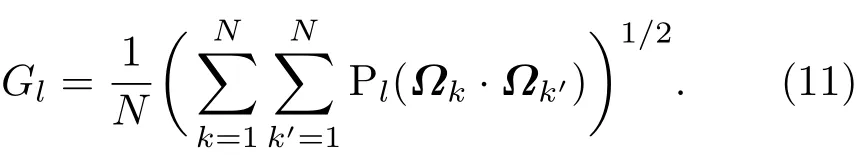
3 模擬分析

3.1 確定待優化入射光束參量

為簡化模型,假設打靶光束為同一波長的非相干光,光束尺寸與靶丸尺寸相近;且束腰足夠長,在靠近靶丸時,可作為平行光束處理,如圖2所示.

常見的入射光束強度模型主要有高斯型(Gaussian)、超高斯型(super-Gaussian)、二次型(quadratic)、平頂型(flat-top)等,其強度分布模型IG,IQ,IF可分別表示為

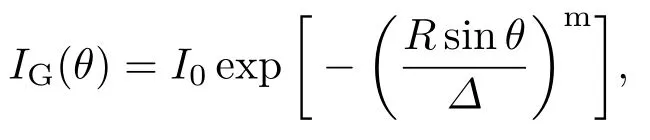
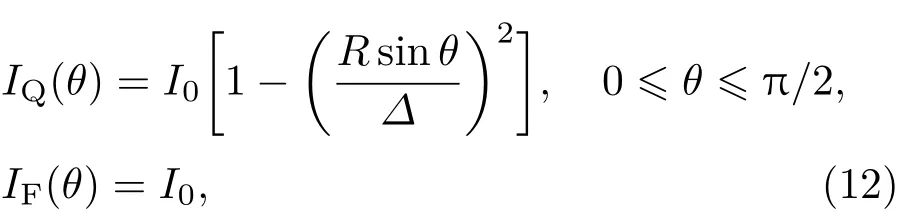
其中I0為光束中心強度,?定義為光束半寬度,R為靶丸半徑,m為超高斯階數,當m=2時,IG為高斯型光束強度分布;當m＞2時,IG為超高斯型光束強度分布.

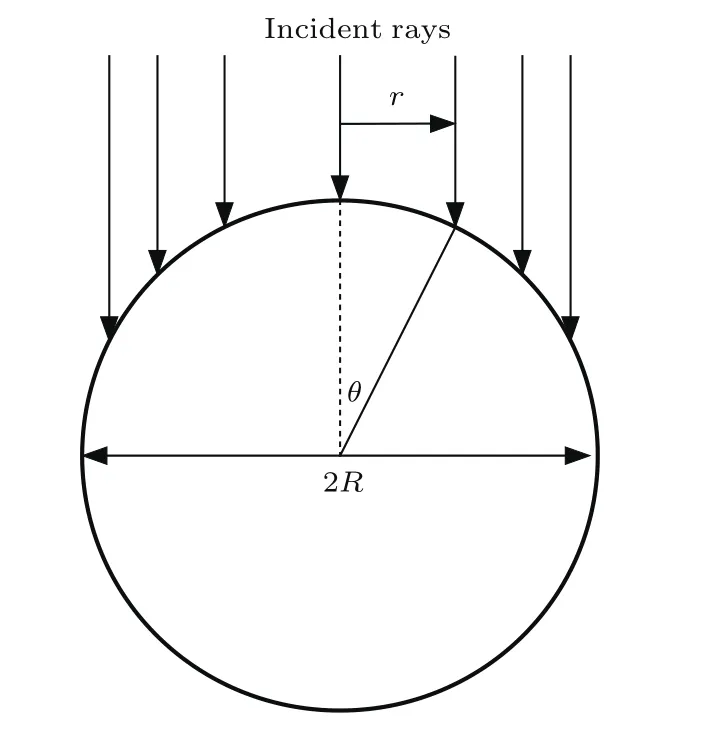
圖2 平行光束輻照靶丸表面的示意圖Fig.2.Schematic drawing of the parallel rays irradiating a target.

根據激光與等離子體相互作用理論,球形靶丸吸收函數A(θ)的表達式[22]為

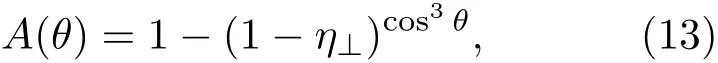
其中η⊥為垂直吸收系數,即當光線垂直照射靶丸表面時的吸收系數,與入射光束的波長相關.

在輻照初期,靶丸表面等離子體層很薄,可忽略其中的折射效應.單一入射光束在靶丸表面的能量沉積Ia(θ)可表示為單一入射光束強度分布Iin(θ)與靶丸表面吸收函數A(θ)的乘積∶

易知0≤θ≤π/2,將(14)式和(13)式代入(9)式中,可得該輻照系統單光束因子項的表達式為

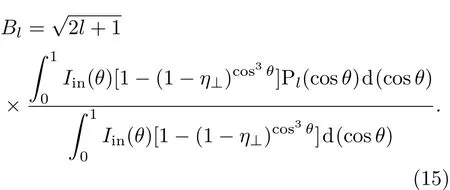
影響單光束因子項的參量主要有光束模型、束寬-靶丸半徑比?/R和垂直吸收系數η⊥,對于超高斯型光束,超高斯階數m對單光束因子項也有影響.本文將對這些影響均勻輻照系統單光束因子項的參量進行詳細分析并給出優化結果.

3.2 入射光束數分析

根據理論分析,為確定幾何因子項,首先需要確定打靶光束數.ICF中,隨著光束數的增加,不僅會增加均勻輻照系統的復雜度和工程難度,而且會提高激光裝置運行中的光束引導和功率平衡難度,并減少留給物理診斷設備的空間,因此靶球上的入射光束數不宜過多.當物理對激光裝置提出較高的總輸出能量要求時,可通過組束打靶的方式將光束編為集束進行打靶.基于上述原因,本文重點討論了光束數N=10—60范圍內的情形.對于更多光束數下的靶丸均勻輻照問題,可參照該方法進行分析和優化.

當光束數N=10—60范圍內,入射光束為高斯型時,系統輻照不均勻度隨光束數的變化曲線如圖3(a)所示.通過在終端光學組件內采用連續相位板等焦斑控制技術,還可在靶丸上獲得超高斯型的焦斑分布.假定入射光束為4階超高斯型,通過模擬可得系統輻照不均勻度隨光束數的變化曲線如圖3(b)所示.

圖3表明,隨著光束數N的增加,靶丸輻照不均勻度呈逐漸減小的趨勢.設定垂直吸收系數η⊥=95%,在高斯型入射光束輻照系統中,N=32對應的系統輻照不均勻度最小;在4階超高斯型入射光束輻照系統中,N=48對應的系統輻照不均勻度最小.32束光排布結構較為特殊,通過本文3.4.1小節的分析可知,在對心角錐排布方案和電子斥力模型方案中,32束光排布結構相同,均基于正十二面體結構,具有進行深入研究分析的價值.而48束光輻照系統在大型激光裝置中有著廣泛應用,如NIF的48個集束打靶和神光-III激光裝置的48束光打靶,因此也具有深入分析的價值.本文對輻照不均勻度的分析以32束光輻照系統[9]和48束光輻照系統[19]為例,其光束方位角在靶丸表面呈環狀分布,具體數據列于表1.

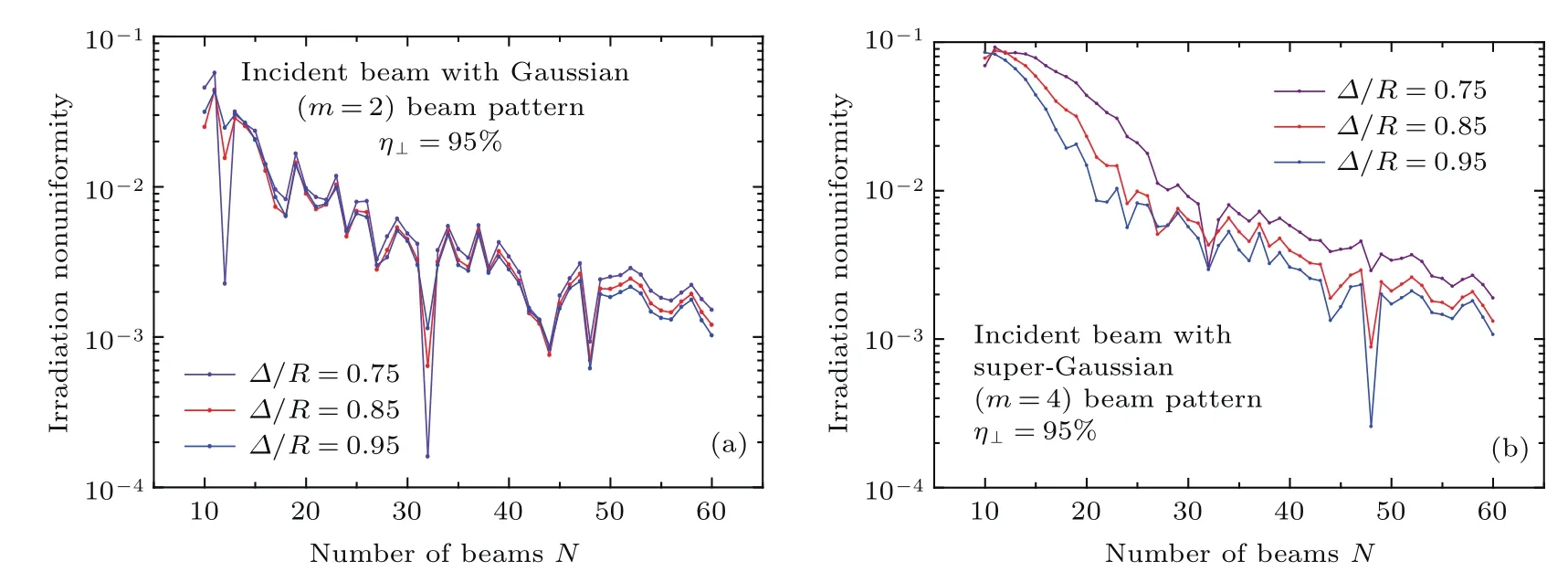
圖3 (網刊彩色)入射光束為(a)高斯型和(b)超高斯型時,不同光束數N對應的靶丸輻照不均勻度Fig.3.(color online)The irradiation nonuniformity calculated when the incident beam with(a)Gaussian distribution and(b)super-Gaussian distribution using different number of beams.

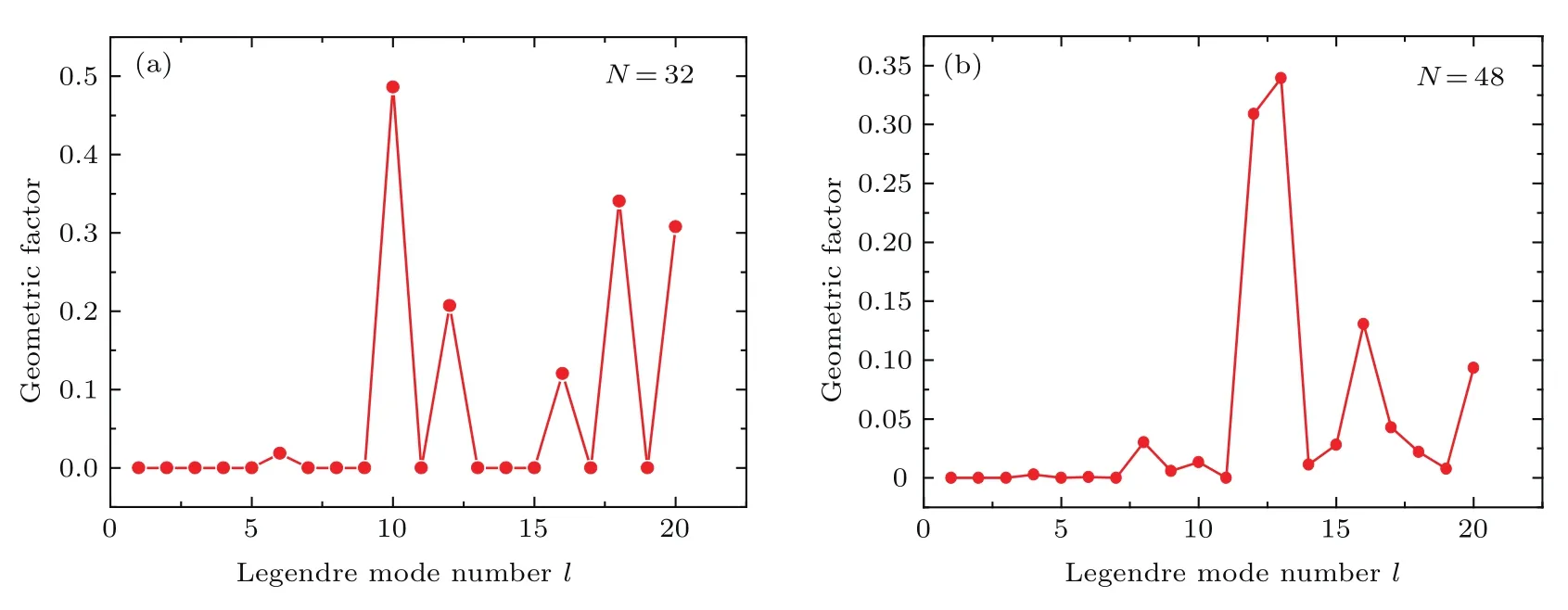
圖4 (a)32束光輻照系統和(b)48束光輻照系統的幾何因子項Fig.4.Geometric factor in the(a)32-beam and(b)48-beam irradiation systems.

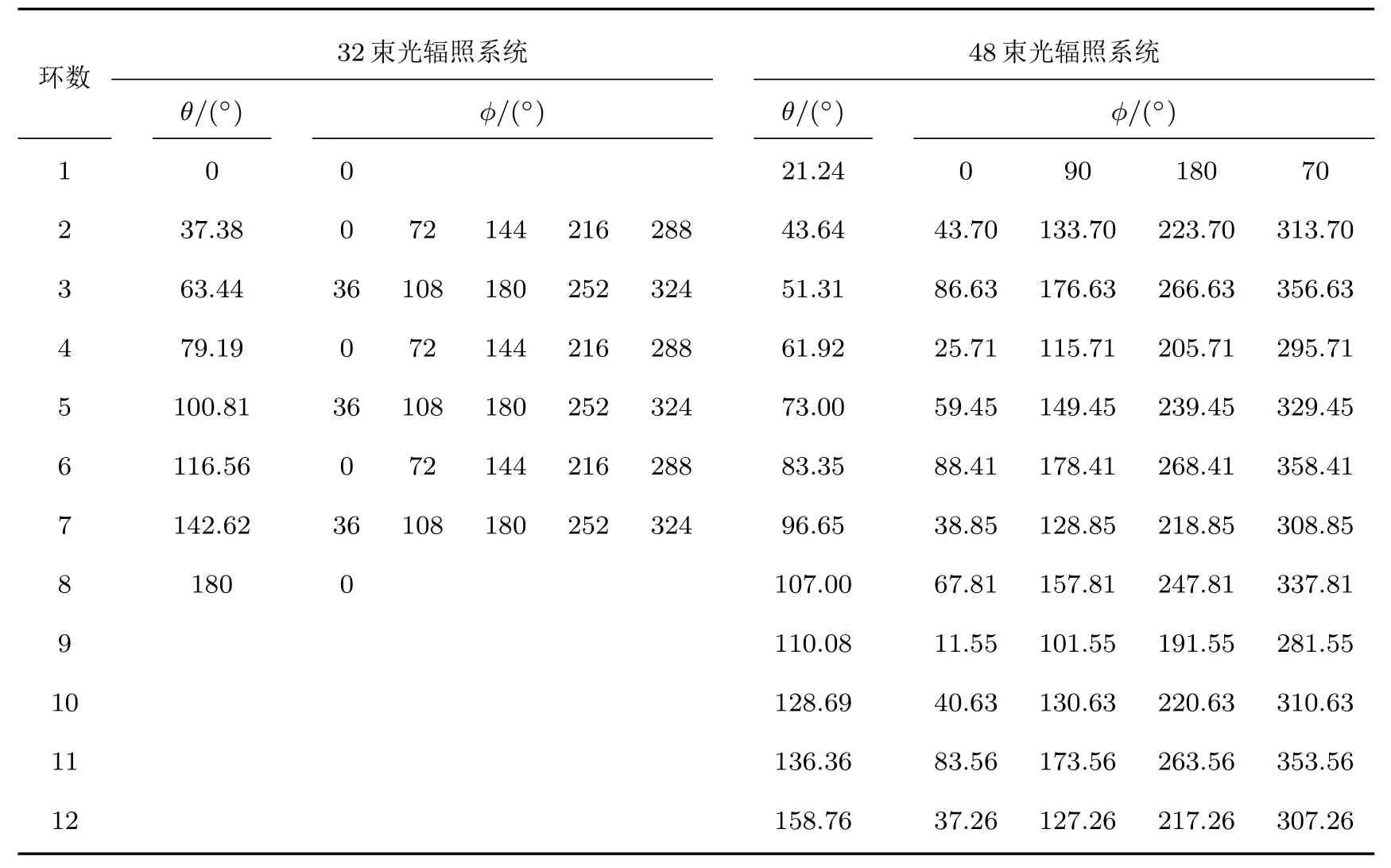
表1 32束光[9]和48束光[19]均勻輻照系統的光束方位角Table 1.Orientation of the beams in the 32-beam[9]and 48-beam[19]irradiation systems.

表1中兩種均勻輻照系統排布結構的幾何因子項(geometric factor)隨勒讓德模階數(Legendre mode number)的變化曲線如圖4所示.

根據上述光束排布結構下幾何因子項的變化趨勢,設GD為最低階主要幾何因子項,Gl＜D均為零,Gl≥D存在非零項.圖4表明,32束光輻照系統最低階主要幾何因子項為G6,Gl＜6近似為零;48束光輻照系統最低階主要幾何因子項為G8,Gl＜8近似為零.在優化單光束因子項時,需要重點考慮單光束因子項收斂趨于零的速度,以及在趨于零后是否有起伏;另外需要考慮單光束因子項與幾何因子項的匹配關系,即非零幾何因子項所對應的單光束因子項要近似為零.

3.3 入射光束模型的優化分析

根據理論分析,對不同入射光束參量的單光束因子項和系統輻照不均勻度進行模擬計算.設入射光束的束寬-靶丸半徑比?/R=0.75,高斯型、超高斯型(以m=4為例)、二次型、平頂型光束在垂直吸收系數η⊥為85%,95%時單光束因子項(single beam factor)隨勒讓德模階數的變化曲線如圖5(a)和圖5(b)所示,在32束光和48束光輻照系統中輻照不均勻度σrms隨垂直吸收系數η⊥的變化曲線如圖5(c)和圖5(d)所示.

對比圖5(a)和圖5(b)可知,入射光束模型對單光束因子項的影響要遠遠大于垂直吸收系數η⊥對單光束因子項的影響.對比四種不同入射光束模型的單光束因子項隨勒讓德模階數的變化曲線,平頂型光束趨于零的速度較慢,且6階—20階勒讓德模起伏較大;二次型光束在第10階趨于零,但在第12階和第15階附近出現起伏;高斯型和超高斯型光束在第10階趨于零后較為穩定,沒有明顯起伏.圖5(c)和圖5(d)顯示,在32束光和48束光輻照系統中,隨著垂直吸收系數η⊥的變化,平頂型光束和二次型光束對應的系統輻照不均勻度一直較大,均不滿足σrms＜1%;而高斯型及超高斯型光束對應的系統輻照不均勻度則滿足σrms＜1%.綜合上述分析,高斯型及超高斯型光束作為入射光束較為合適.

2014年中國科學技術大學徐騰[23]在其博士論文中給出了η⊥=95%和?/R=0.75時4階超高斯型光束單光束因子項Bl隨勒讓德模階數l的變化,具體數據如表2所列.將表2中的數據與圖5(b)中4階超高斯型光束單光束因子項隨勒讓德模階數的變化曲線進行對比,二者完全符合,從而證明了本文對單光束因子項的理論分析以及模擬計算的正確性.

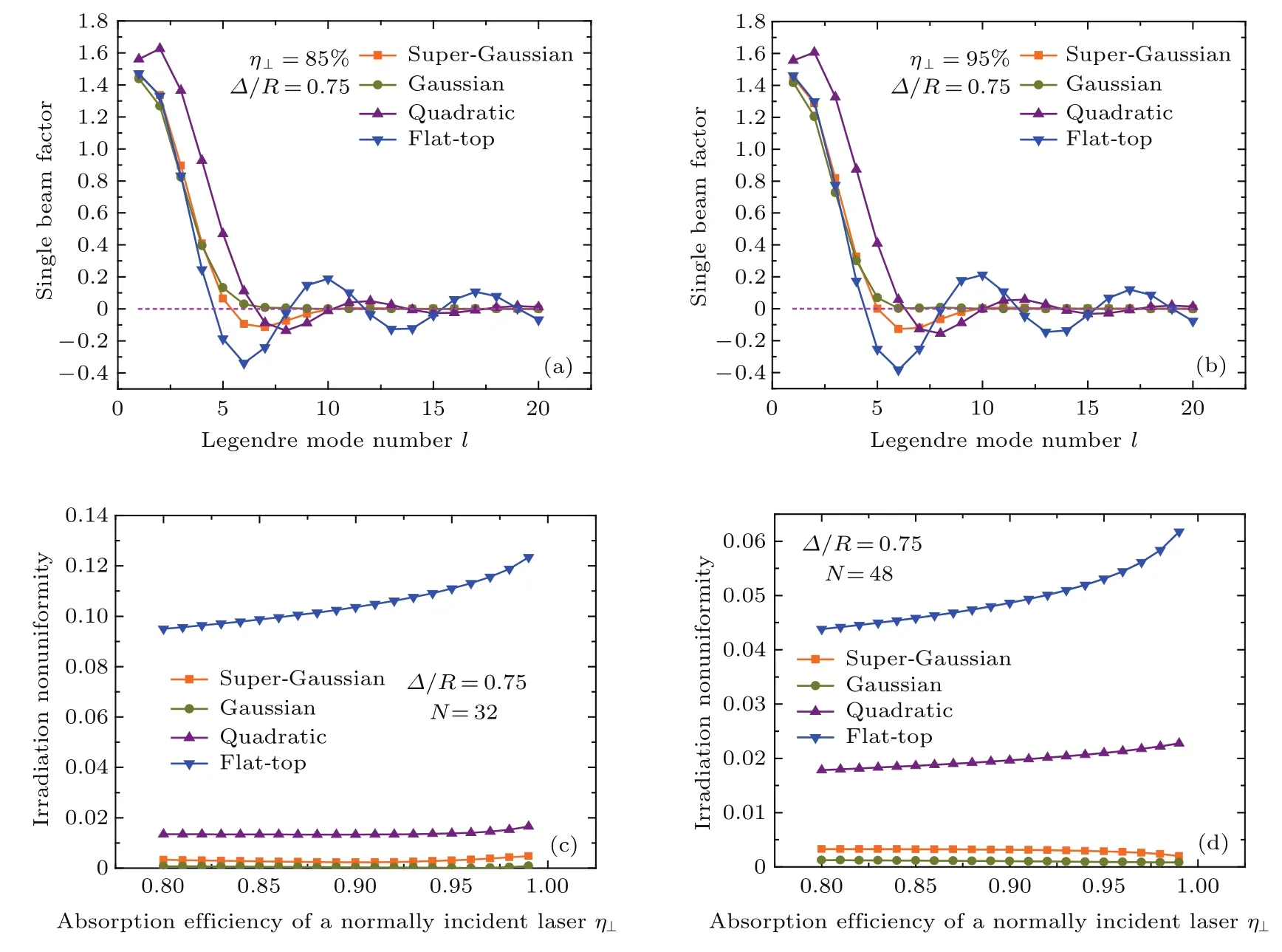
圖5 (網刊彩色)不同光束模型在給定參數下的單光束因子項及其在32束光和48束光輻照系統中的輻照不均勻度(a)?/R=0.75,η⊥=85%;(b)?/R=0.75,η⊥=95%;(c)?/R=0.75,N=32;(d)?/R=0.75,N=48Fig.5.(color online)The single beam factor and irradiation nonuniformity of different beam patterns in the 32-beam and 48-beam irradiation systems for the given parameters:(a)?/R=0.75,η⊥=85%;(b)?/R=0.75,η⊥=95%;(c)?/R=0.75,N=32;(d)?/R=0.75,N=48.

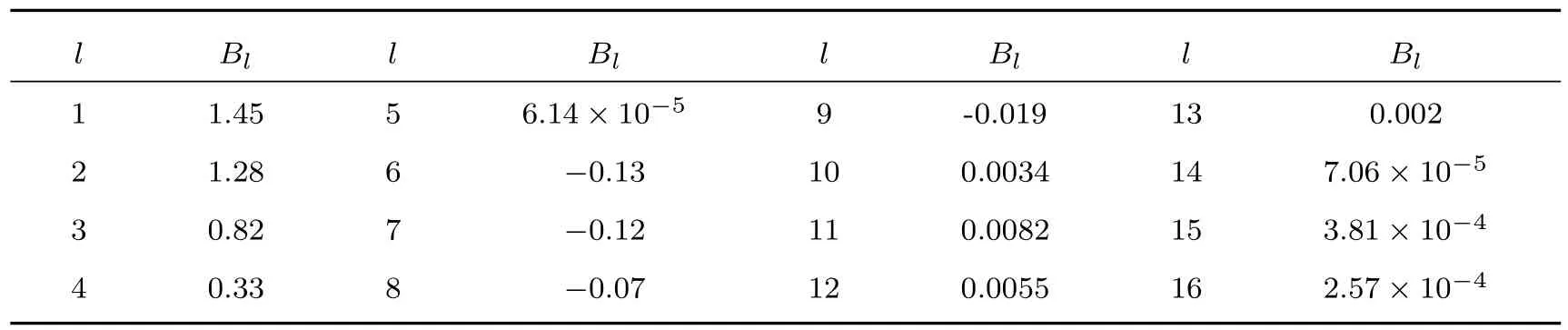
表2 當4階超高斯型光束參量為η⊥=95%和?/R=0.75時,勒讓德模階數l對應的單光束因子項Bl[23]Table 2.The single beam factor Blversus the Legendre mode numberlfor the super-Gaussian beam pattern(m=4)with η⊥=95%and ?/R=0.75[23].

3.4 不同階數超高斯型光束的對比分析

根據上述分析,設定入射光束為超高斯型光束.在高功率激光裝置中,可通過采用CPP等相位板技術在靶丸表面獲得超高斯型的光束分布,超高斯階數m一般為2,4,6,8,10,12等偶數階.根據超高斯光束的強度分布特征,當超高斯階數過高時,其強度分布接近于平頂型.由上述分析可知,平頂型光束的單光束因子項并不理想,對應的系統輻照不均勻度σrms較大.因此在直接驅動靶丸均勻輻照的優化過程中,要注意控制超高斯階數m的取值不能過高,這里將討論超高斯階數分別為2,4,6,8,10和12時對均勻輻照系統的影響.

3.4.1 32束光輻照系統

利用對心角錐排布方案的光束方位角數據[9]和Murakami等[19]通過電子斥力模型方法計算得到的光束方位角,通過本文的計算方法可得幾何因子項隨勒讓德模階數的變化曲線,如圖6所示.圖中,P32和M32分別代表對心角錐排布方案和電子斥力模型方法得到的32束光排布結構.

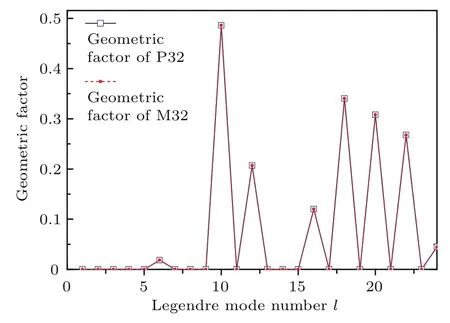
圖6 (網刊彩色)P32和M32中的幾何因子項Fig.6.(color online)The geometric factor of P32 and M32.

圖6表明,基于對心角錐排布方案和電子斥力模型方案得到的幾何因子項隨勒讓德模階數的變化曲線相同,這與Murakami等[19]的模擬結果一致,從而證明了本文對幾何因子項的理論分析及模擬計算的正確性.

將垂直吸收系數也作為變量進行模擬計算,當入射的超高斯型光束階數m為2,4,6,8,10,12時,模擬計算得到的32束光輻照系統的輻照不均勻度等高圖如圖7所示.圖中橫坐標為垂直吸收系數η⊥,縱坐標為束寬-靶丸半徑比?/R.

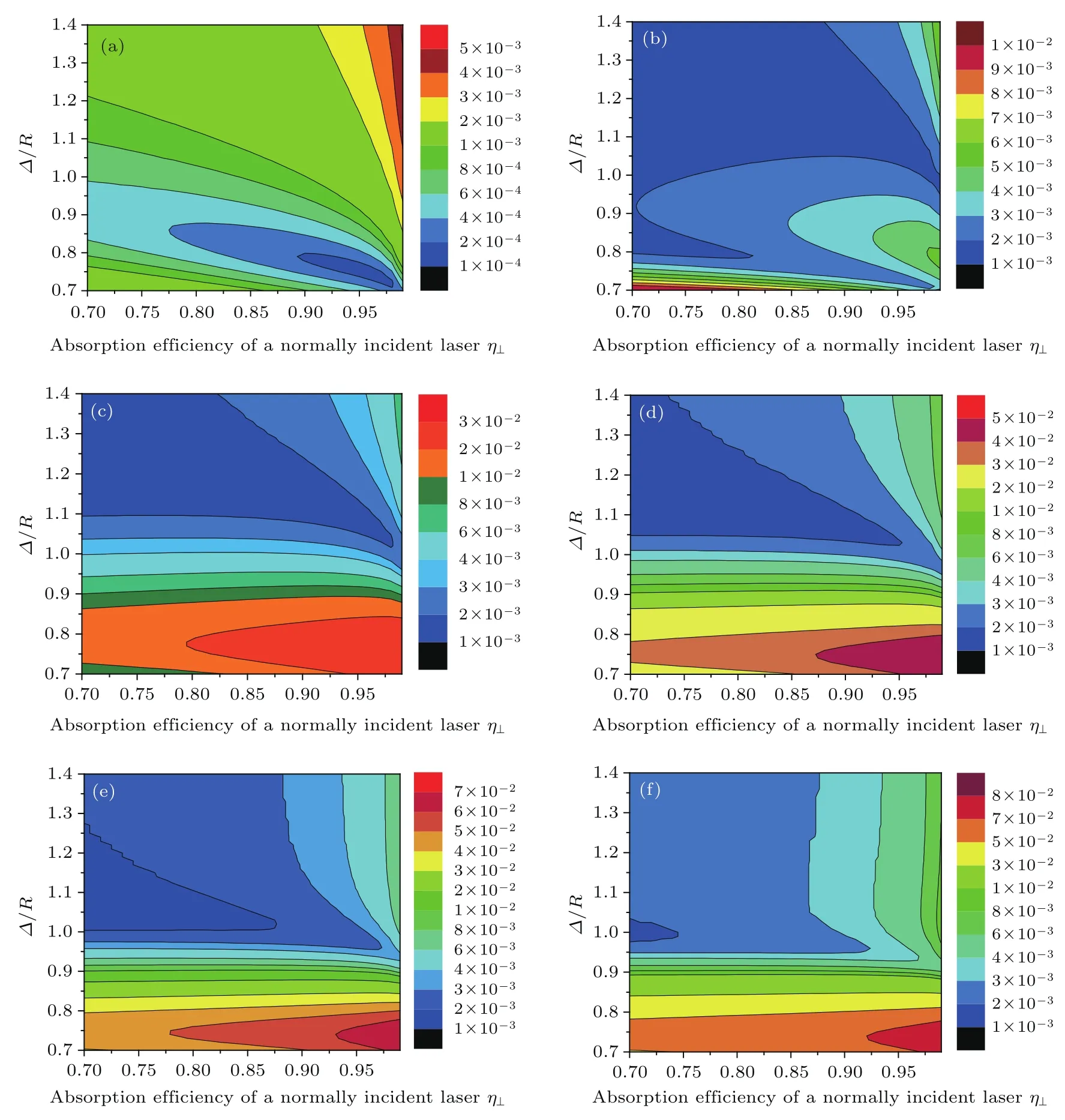
圖7 (網刊彩色)32束光輻照系統中不同階數超高斯型光束的輻照不均勻度 (a)m=2;(b)m=4;(c)m=6;(d)m=8;(e)m=10;(f)m=12Fig.7.(color online)The irradiation nonuniformity of the Gaussian and super-Gaussian beam patterns in the 32-beam irradiation system:(a)m=2;(b)m=4;(c)m=6;(d)m=8;(e)m=10;(f)m=12.

圖7表明,在32束光輻照系統中,系統輻照不均勻度隨著超高斯階數m的增大呈現整體增大的趨勢.當m=2時,隨著?/R的變化,其輻照不均勻度數值均比較小,在圖示參量范圍內,均處于0.5%以下,該特性很好地抑制了靶丸壓縮過程中?/R發生變化所帶來的輻照不均勻;當m=6時,圖7(c)中橙色和紅色區域內σrms＞ 1%,不再滿足直接驅動中靶丸均勻壓縮的條件;同時參量?/R和η⊥對系統輻照不均勻度也存在一定的影響,當m一定時,若?/R較小時,則?/R對輻照不均勻度的影響占主導地位,若?/R較大,則η⊥對輻照不均勻度的影響占主導地位.另外從圖7中可知,不同超高斯階數m的入射光束對應的最佳垂直吸收系數η⊥與束寬-靶丸半徑比?/R不同.對比輻照不均勻度等高圖,可以得出∶各入射光束參量的最佳匹配位置在m=2,η⊥=96%,?/R=0.75處,此時系統的輻照不均勻度達到最小值σrms=0.012%,接近完全均勻輻照,而且在最佳參量附近,輻照不均勻度變化不明顯,當參量η⊥=95%,?/R=0.7557,m=1.9981時,其σrms=0.012%.

這一計算結果與2016年Li等[24]的模擬結果一致,Li等利用粒子梯度力模型對32束光輻照系統的輻照不均勻度進行的模擬優化結果顯示∶設定垂直吸收系數為95%,對于超高斯型入射光束,當m=1.9981,?/R=0.7557時,系統輻照不均勻度最小,其值為σrms=0.0121%.從而證明了本文對輻照不均勻度的理論分析及模擬計算的正確性.

由上述分析可知,對于32束光輻照系統,入射光束選取高斯型光束,參數η⊥=96%,?/R=0.75時,系統輻照均勻度最佳,接近完全均勻輻照.由于直接驅動對靶丸輻照初期的光場輻照均勻度要求最高,該系列參數可作為系統的初始均勻輻照參數.

為了分析32束光輻照系統在輻照均勻性最佳時各入射光束參量的特征,圖8給出了m=2時幾組不同入射光束參量下的單光束因子項.由圖可見,入射光束的單光束因子項從第10階開始都近似為零.從圖4(a)可知,32束光排布方案的幾何因子項前5項為零,所以第6—9階單光束因子項造成了輻照不均度的差異.如圖8所示,不同入射光束參量的第7—9階單光束因子項基本相同,而且數值很小,所以輻照不均勻度的差異主要是由第6階單光束因子項造成的.當η⊥=96%,?/R=0.75時,第6階單光束因子項極小,其絕對值為0.0002,分別是η⊥=75%,?/R=0.75時的1/250,是η⊥=96%,?/R=0.95時的1/200.對比幾何因子項與單光束因子項可知,在32束光輻照系統中,入射光束為高斯型光束,參量η⊥=96%,?/R=0.75時,滿足單光束因子項與幾何因子項的匹配關系,即非零幾何因子項所對應的單光束因子項近似為零.

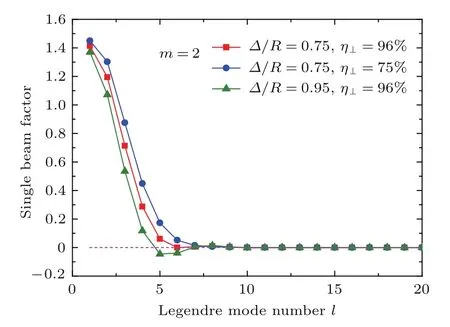
圖8 (網刊彩色)高斯型光束三組不同參數下的單光束因子項Fig.8.(color online)The single beam factor of the Gaussian beam pattern with different parameters.

綜上所述,32束光輻照系統在單光束因子項與幾何因子項滿足匹配關系時,系統均勻輻照性能最佳.另外,32束光排布方案基于正十二面體結構,而這類排布結構的第6階幾何因子項不為零[17],因此設法消除第6階勒讓德模帶來的輻照不均勻度是這類系統調控時需考慮的重點問題.當入射光束為高斯光束,且光束參量?/R=0.75,η⊥=96%時,其極小的第6階單光束因子項可解決上述問題.

3.4.2 48束光輻照系統

對48束光輻照系統中輻照不均勻度進行了模擬計算,當入射光束的超高斯階數m為2,4,6,8,10,12時,輻照不均勻度的等高圖如圖9所示.

圖9顯示,在48束光輻照系統中,隨著超高斯階數m的增加,系統輻照不均勻度整體增大.在m=6時,圖9(c)中的紅色區域σrms＞ 1%,已經不能滿足直接驅動靶丸均勻壓縮的要求,而且隨著m的增大,σrms＞1%的區域也逐漸增大.同時與32束光輻照系統相似,當m一定時,若?/R較小,則?/R對輻照不均勻度的影響占主導地位,若?/R較大,則η⊥對輻照不均勻度的影響占主導地位.另外,不同超高斯階數m的入射光束對應的最佳垂直吸收系數η⊥與束寬—靶丸半徑比?/R不同,在圖9(b)中深藍色區域出現輻照不均勻度極小值,即當光束參數m=4,η⊥=94%,?/R=0.97時,系統輻照不均勻度最小,其值為σrms=0.0262%,此時?/R在圖9(b)所示范圍內變化時,系統輻照不均勻度均小于0.5%,滿足直接驅動的靶丸均勻壓縮條件.通過上述分析可知,對于48束光直接驅動均勻輻照系統,當入射光束為4階超高斯型光束,參數η⊥=94%,?/R=0.97時,系統輻照均勻度最佳.

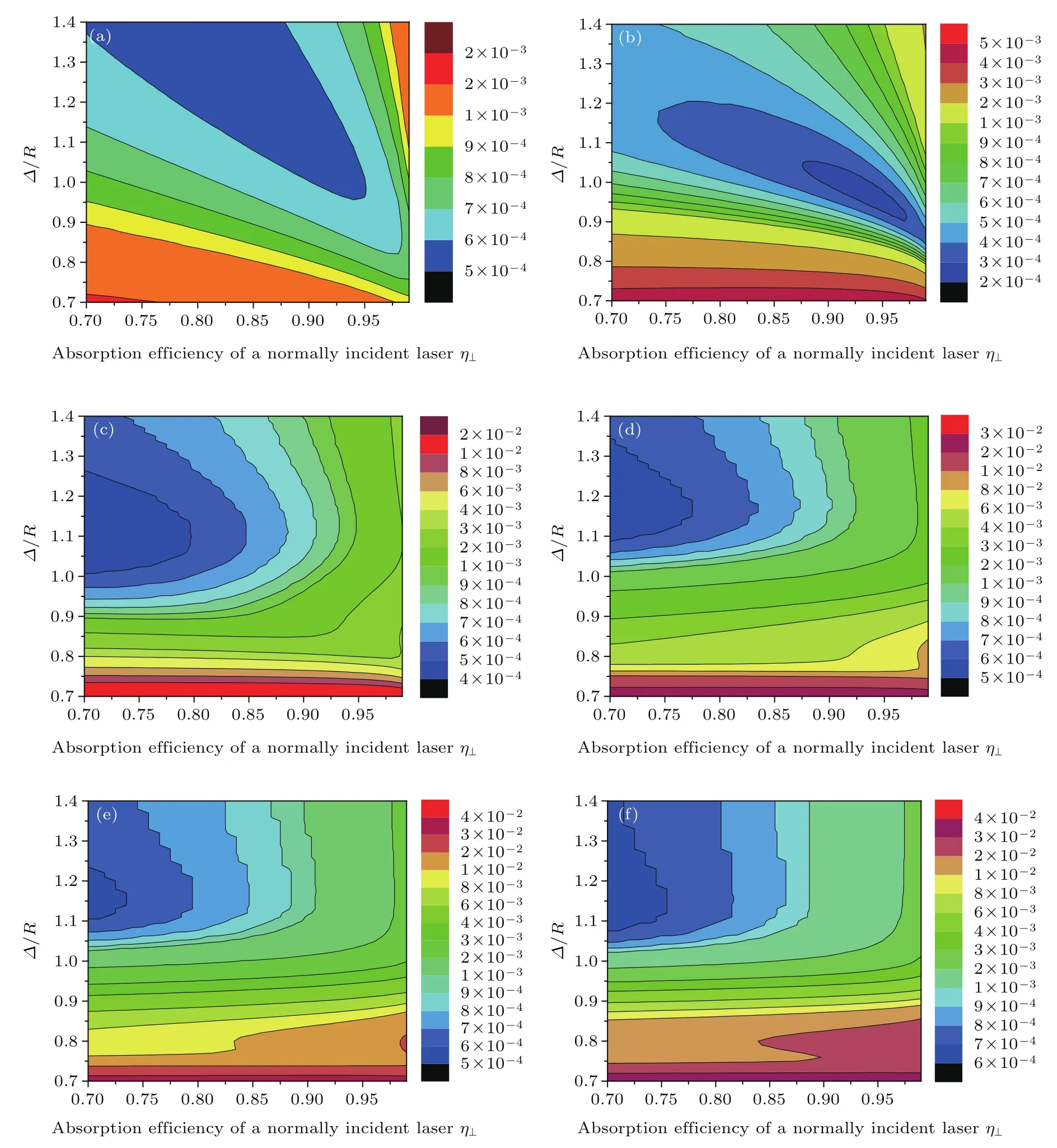
圖9 (網刊彩色)48束光輻照系統中不同階數超高斯型光束的輻照不均勻度 (a)m=2;(b)m=4;(c)m=6;(d)m=8;(e)m=10;(f)m=12Fig.9.(color online)The irradiation nonuniformity of Gaussian and super-Gaussian beam patterns in the 48-beam irradiation system:(a)m=2;(b)m=4;(c)m=6;(d)m=8;(e)m=10;(f)m=12.

圖10給出了4階超高斯型光束在不同參量時的單光束因子項,由圖可以看出從第10階開始,入射光束的單光束因子項基本相同,其值均接近零.從圖4(b)中可知,48束光輻照系統的最低階主要幾何因子項為G8,即前7階幾何因子項均接近于零,且G9遠小于G8.因此在本文所述的48束光直接驅動光束排布方案中,對輻照不均勻度有貢獻的單光束因子項為B8?9,且B8＞B9,所以第8階輻照不均勻度為主要部分.由圖10可知,參量η⊥=94%,?/R=0.97時,4階超高斯型入射光束第8階單光束因子項很小,絕對值為0.004;分別為η⊥=94%,?/R=0.97時的1/4,η⊥=94%,?/R=0.97時的1/15.對比幾何因子項與單光束因子項可知,在48束光均勻輻照系統中,入射光束為4階超高斯型光束,參量η⊥=94%,?/R=0.97時,滿足單光束因子項與幾何因子項的匹配關系,即非零幾何因子項所對應的單光束因子項近似為零,因此系統均勻輻照性能最佳.

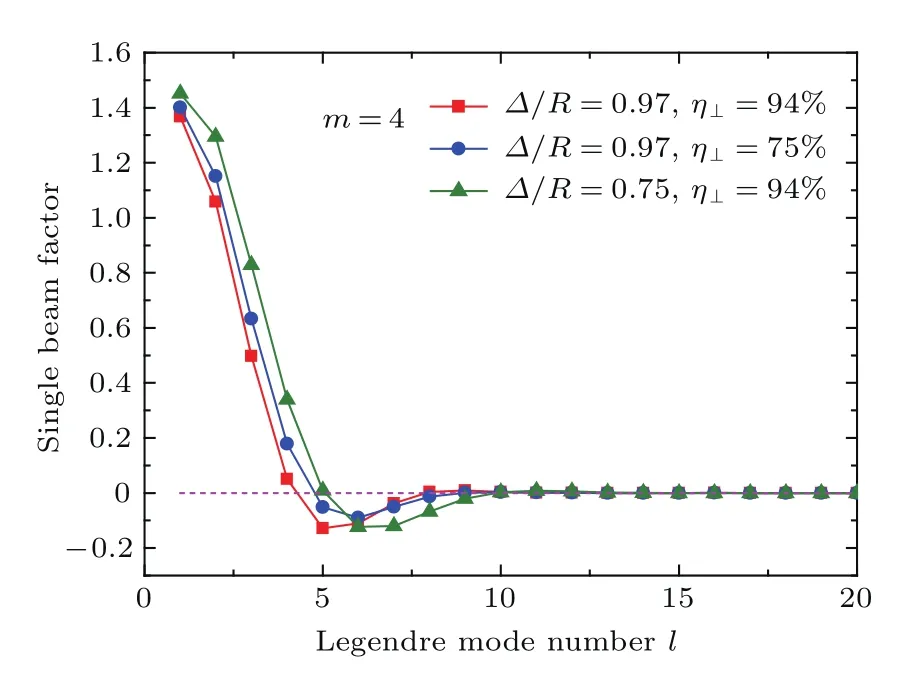
圖10 (網刊彩色)采用4階超高斯型光束和不同?/R,η⊥時的單光束因子項Fig.10.(color online)The single beam factor using super-Gaussian beam pattern(m=4)and different?/R and η⊥ parameters.

4 總 結

本文通過理論分析,對32束光輻照系統和48束光輻照系統的輻照不均勻度進行了模擬計算,結果顯示∶在32束光和48束光輻照系統中,入射光束模型對系統輻照不均勻度的影響較為明顯,其次為垂直吸收系數η⊥和束寬-靶丸半徑比?/R.且入射光束模型確定后,當?/R較小時,?/R對輻照不均勻度的影響占主導地位;?/R較大時,η⊥對輻照不均勻度的影響占主導地位.因此在入射光束參量優化過程中,需要首先對入射光束模型進行優化,然后優化分析參量?/R和η⊥.對于32束光輻照系統,最優入射光束為高斯型,參量最佳值為η⊥=96%,?/R=0.75,其第六階單光束因子項B6近似為零,這一特性對于基于正十二面體的排布結構極為有利,可解決基于正十二面體排布結構的第六階幾何因子項G6不為零的問題.對于48束光輻照系統,最優入射光束為4階超高斯型,參量最佳值為η⊥=94%,?/R=0.97.32束光和48束光輻照系統的入射光束參量為最佳值時,系統輻照不均勻度對聚焦光束寬度與靶丸半徑比的變化均有較高的穩定性,可減輕ICF靶丸壓縮過程中由于?/R發生變化所帶來的輻照不均勻.

通過模擬對比分析可知,當幾何因子項與單光束因子項滿足匹配關系時,系統均勻輻照性能最佳,即對于不同的打靶光束數和光束排布結構,均有與之對應的最優入射光束參量,可使輻照不均勻度達到最小值.基于上述結論,本文提出了一種優化直接驅動靶丸均勻輻照性能的新方法,在已知的光束排布結構中,通過對幾何因子項特性的分析,求取與之匹配的單光束因子項,從而獲得最佳的入射光束參量,使均勻輻照系統達到最優化.這一優化思路和文中模擬分析結果對直接驅動均勻輻照系統中打靶光束的光束模型選取、聚焦光束寬度選擇和垂直吸收系數的優化均具有一定的指導意義.

在本工作的基礎上,后續研究中將進一步考慮各種實際光束參量,如帶寬、聚焦光束打靶產生的散斑、束勻滑技術等對靶丸均勻輻照的影響;并將優化結果與光束控制技術銜接,從而對空域、時域和頻域束勻滑技術的優化提供指導.

[1]Lindl J 1995 Phys.Plasmas 2 3933

[2]Miller G H,Moses E I,Wuest C R 2004 Opt.Eng.43 2841

[3]Fleurot N,Cavailler C,Bourgade J L 2005 Fusion Eng.Des.74 147

[4]Zheng W,Zhang X,Wei X,Jing F,Sui Z,Zheng K,Yuan X,Jiang X,Su J,Zhou H,Li M 2008 J.Phys.Conf.Ser.112 032009

[5]Bodner S E,Colombant D G,Gardner J H,Lehmberg R H,Obenschain S P,Phillips L,Schmitt A J,Sethian J D,McCrory R L,Seka W,Verdon C P 1998 Phys.Plasmas 5 1901

[6]Hallo L,Olazabal-Loumé M,Ribeyre X,Dréan V,Schurtz G,Feugeas J L,Breil J,Nicola? P,Maire P H 2008 Plasma Phys.Control.Fusion 51 014001

[7]Boehly T R,Brown D L,Craxton R S,Keck R L,Knauer J P,Kelly J H,Kessler T J,Kumpan S A,Loucks S J,Letzring S A,MarshallfJ 1997 Opt.Commun.133 495

[8]Bodner S E 1981 J.Fusion Energy 1 221

[9]Skupsky S,Lee K 1983 J.Appl.Phys.54 3662

[10]Emery M H,Gardner J H,Boris J P 1982 Phys.Rev.Lett.48 677

[11]Gardner J H,Bodner S E 1981 Phys.Rev.Lett.47 1137

[12]Zhang R,Li P,Su J Q,Wang J J,Li H,Geng Y C,Liang Y,Zhao R C,Dong J,Lu Z G,Zhou L D,Liu L Q,Lin H H,Xu D P,Deng Y,Zhu N,Jing F,Sui Z,Zhang X M 2012 Acta Phys.Sin.61 054204(in Chinese)[張銳,李平,粟敬欽,王建軍,李海,耿遠超,梁樾,趙潤昌,董軍,盧宗貴,周麗丹,劉蘭琴,林宏奐,許黨朋,鄧穎,朱娜,景峰,隋展,張小民2012物理學報61 054204]

[13]Liu L Q,Zhang Y,Geng Y C,Wang W Y,Zhu Q H,Jing F,Wei X F,Huang W Q 2014 Acta Phys.Sin.63 164201(in Chinese)[劉蘭琴,張穎,耿遠超,王文義,朱啟華,景峰,魏曉峰,黃晚晴2014物理學報63 164201]

[14]Li P,Wang W,Zhao R C,Geng Y C,Jia H T,Su J Q 2014 Acta Phys.Sin.63 215202(in Chinese)[李平,王偉,趙潤昌,耿遠超,賈懷庭,粟敬欽 2014物理學報 63 215202]

[15]Garanin S G,Derkach V N,Shnyagin R A 2004 Quantum Electron.34 427

[16]Schmitt A J 1984 Appl.Phys.Lett.44 399

[17]Murakami M 1995 Appl.Phys.Lett.66 1587

[18]Seidel J J 2001 J.Stat.Plan.Infer.95 307

[19]Murakami M,Sarukura N,Azechi H,Temporal M,Schmitt A J 2010 Phys.Plasmas 17 082702

[20]Xu T,Xu L,Wang A,Gu C,Wang S,Liu J,Wei A 2013 Phys.Plasmas 20 122702

[21]Temporal M,Canaud B,Garbett W J,Ramis R 2015 Phys.Plasmas 22 102709

[22]Kruer W L 2003 The Physics of Laser Plasma Interactions(Oxford:Westview Press)p45

[23]Xu T 2014 Ph.D.Dissertation(Hefei:University of Science and Technology of China)(in Chinese)[徐騰 2014博士學位論文(合肥:中國科學技術大學)]

[24]Li L,Gu C,Xu L,Zhou S 2016 Phys.Plasmas 23 043103

PACS∶52.57.—z,42.79.—e,42.60.JfDOI∶10.7498/aps.66.105202

*Project supported by the National Natural Science Foundation of China(Grant No.61475145).

?Corresponding author.E-mail:zhangrui8s-1@caep.cn

Uniform irradiation of a direct drive target by optimizing the beam parameters?

Li Hong-Xun1)2)Zhang Rui1)?Zhu Na1)Tian Xiao-Cheng1)Xu Dang-Peng1)Zhou Dan-Dan1)Zong Zhao-Yu1)Fan Meng-Qiu1)Xie Liang-Hua1)2)Zheng Tian-Ran1)2)Li Zhao-Li1)2)
1)(Laser Fusion Research Center,China Academy of Engineering Physics,Mianyang 621900,China)
2)(Graduate Schoolof China Academy of Engineering Physics,Beijing 100088,China)

20 December 2016;revised manuscript

7 March 2017)

Laser driven fusion requires a high-degree uniformity in laser energy deposition in order to achieve the high-density compression required for sustaining a thermonuclear burn.Nowadays,uniform irradiation of capsule is still a key issue in direct drive inertial confinement fusion.The direct drive approach is to drive the target with laser light,by irradiating it with a large number of overlapping laser beams.In the direct drive scheme,the laser deposition pattern on the target can be decomposed into a series of Legendre spherical harmonic modes.The high mode(shorter wavelength)nonuniformity can lead to Rayleigh-Taylor instability,which may result in the failure of target compression.This nonuniformity can be suppressed by thermal conduction and beam conditioning technologies,such as continuous phase plate,smoothing by spectral dispersion and polarization smoothing.The low mode(longer wavelength)nonuniformity is related to the number,orientation and power balance of laser beams,which is hard to suppress by thermal conduction and beam conditioning technologies.Generally,the nonuniformity of laser irradiation on a directly driven target should be less than 1%(root mean square,RMS),to meet the requirement for symmetric compression.Several methods have been proposed to optimize the irradiation configuration in direct drive laser fusion,such as truncated icosahedron with beams at the 20 faces and 12 vertices of an icosaherdron,dodecahedron-based irradiation configurations,self-organizing electrodynamic method,etc.However,limited by the different parameters of incident beams,the irradiation uniformity is often not satisfactory.Therefore,it is necessary tofind new way to improve the irradiation uniformity and make it more robust.According to the analytical result,the irradiation nonuniformity can be decomposed into the single beam factor and the geometric factor.Simulation results show that the single beam factor is mainly determined by the parameters of the incident beams,including beam pattern,beam width and beam wavelength.By analyzing and simulating the single beam factor with different incident beam parameters,and comparing the single beam factor with the geometric factor,a matching relationship between them is found by using the optimized parameters.Based on the simulation results,a method to optimize the incident beam parameters is proposed,which is applied to the 32-beam and 48-beam irradiation configurations.The results show that there is a set of optimal incident beam parameters which can attain the highest irradiation uniformity for a given configuration.The feasibility to achieve more uniform irradiation by optimizing the incident beam parameters is proved.When the single beam factor is optimized in a directly driven inertial confinement fusion system,the restrictions on the beam pointing error and power imbalance between incident beams can be relaxed.The results provide an effective method of designing and optimizing the uniform irradiation system of direct drive laser facility.

∶inertial confinement fusion,direct drive,irradiation uniformity,incident beam parameters

?國家自然科學基金(批準號:61475145)資助的課題.

?通信作者.E-mail:zhangrui8s-1@caep.cn

?2017中國物理學會Chinese Physical Society