雙饋型風電系統變流器控制參數對振蕩模態的影響

吳汪平, 解 大, 趙祖熠, 魯玉普, 楚皓翔

(上海交通大學 電子信息與電氣工程學院，上海 200240)

雙饋型風電系統變流器控制參數對振蕩模態的影響

吳汪平, 解 大, 趙祖熠, 魯玉普, 楚皓翔

(上海交通大學 電子信息與電氣工程學院，上海 200240)

研究雙饋型風力發電系統變流器控制參數對振蕩模態的影響。在MATLAB/Simulink中建立系統詳細的小信號模型，利用特征值分析和相關因子分析，對機網相互作用振蕩模態進行辨識和分類。通過改變變流器控制參數，研究振蕩模態的變化特性。最后，在MATLAB/Simulink上進行仿真驗證。研究表明，優化變流器控制參數，可有效抑制振蕩。

風電場; 變流器; 雙饋感應發電機; 振蕩模態

0 引 言

研究發現，風電場與電網之間的相互作用多表現為有功功率的振蕩，與此同時，大規模風電機組出現脫網事故。上述機網振蕩問題已引起國內外學者的關注與研究[1-2]。振蕩可能會加重風電機組中機械部件負擔，進而對其機械部件使用壽命造成影響。在我國新疆、河北和營口等大型風電場，就多次出現過因軸系振蕩帶來的齒輪箱和槳葉破損甚至斷裂的現象。如果能對風電機組進行詳細分析，挖掘振蕩中諸如振蕩頻率等詳細特征，采取措施抑制振蕩，將對風電場的安全和穩定運行有重大的意義。

針對機網間振蕩問題，國內外學者展開了很多研究。文獻[3]基于阻尼正弦原子分解的次同步振蕩模態辨識方法，辨識出次同步振蕩模態。文獻[4]研究了雙饋風電場抑制系統次同步振蕩的機理，對比分析了不同的附加阻尼控制策略。文獻[5]分析次同步振蕩的規律，研究速度反饋型PSS與功率反饋型PSS對次同步振蕩的影響機制。文獻[6]研究了SVC接入位置等對次同步振蕩的影響機理，并設計了相應的控制策略。文獻[7]分析了STATCOM附加電壓控制抑制電力系統次同步諧振的作用機理。文獻[8]研究了轉速、串補度、控制器參數對風機串補系統次同步諧振特性的影響。文獻[9]研究STATCOM抑制SSR的機制，提出了一種基于扭振模態互補頻率電流補償的STATCOM次同步諧振控制方法。文獻[10]分析了次同步控制相互作用的機理，推導出次同步控制相互作用存在的條件。文獻[11]研究了異步發電機效應和次同步控制相互作用，分析了串補度和風速變化對次同步控制相互作用的影響。文獻[12]分析了風速、串補度和控制器參數對次同步控制相互作用的影響。文獻[13]分析了雙饋風電場的電力系統低頻振蕩特性，研究了風電場不同運行工況、接入容量,以及是否參與無功調度對系統低頻振蕩的影響。文獻[14]分析雙饋風電機組并網后對電力系統低頻振蕩特性的影響。以上參考文獻只是研究了機網振蕩模態的某一種，未考慮多模態之間相互作用的影響。

本文首次將變流器控制與機網振蕩的多種模態聯系起來，研究控制參數對振蕩模態的影響。本文以雙饋型風力發電系統單機-無窮大系統為例，搭建了機網統一模型；分析系統的振蕩模態，基于相關因子表分析相關的狀態變量，利用時域仿真驗證模態的存在性；研究控制參數對系統振蕩的影響，最后通過時域仿真進行驗證。這意味著不用增加額外裝置，也不用損失系統部分功率，僅通過控制參數優化，即可達到削弱系統振蕩的目的。

1 雙饋型風力發電系統的機網統一模型

圖1為雙饋型風力發電系統單機-無窮大系統拓撲結構。風機葉片經過低速軸與齒輪箱相連，齒輪箱經過高速軸與感應發電機相連。雙饋型風電機組定子回路直接與電網相連，轉子回路則通過電力電子變流器與電網相連。

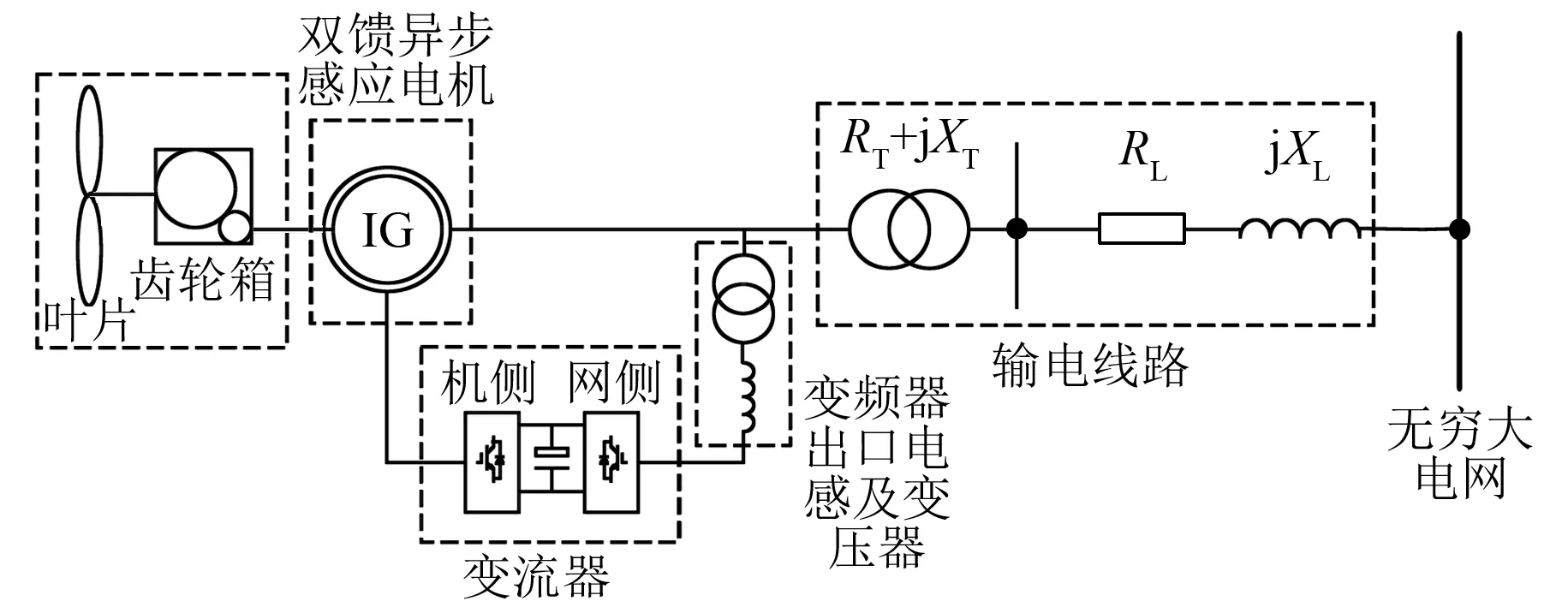
圖1 雙饋風力發電系統并網結構圖

變流器控制中，在機側添加轉子控制，采用定子功率外環和電流內環控制，控制框圖如圖2(a)所示。電網側的變流器則負責穩定直流電容兩端的電壓，控制框圖如圖2(b)所示。圖2中，Kp0和Ki0是轉子角速度控制器PI參數；Kp1和Ki1是定子有功功率控制器PI參數；Kp2和Ki2是轉子電流交軸分量控制器PI參數；Kp3和Ki3是定子無功功率控制器PI參數；Kp4和Ki4是轉子電流直軸分量控制器PI參數。對于網側變流器，其中Kp5和Ki5是直流電壓控制器PI參數；Kp6和Ki6是網側電流直軸分量控制器PI參數；Kp7和Ki7是網側電流交軸分量控制器PI參數。

在MATLAB/Simulink中搭建圖1所示系統的小信號模型，各個模塊的接口連接圖如圖3所示[15]。

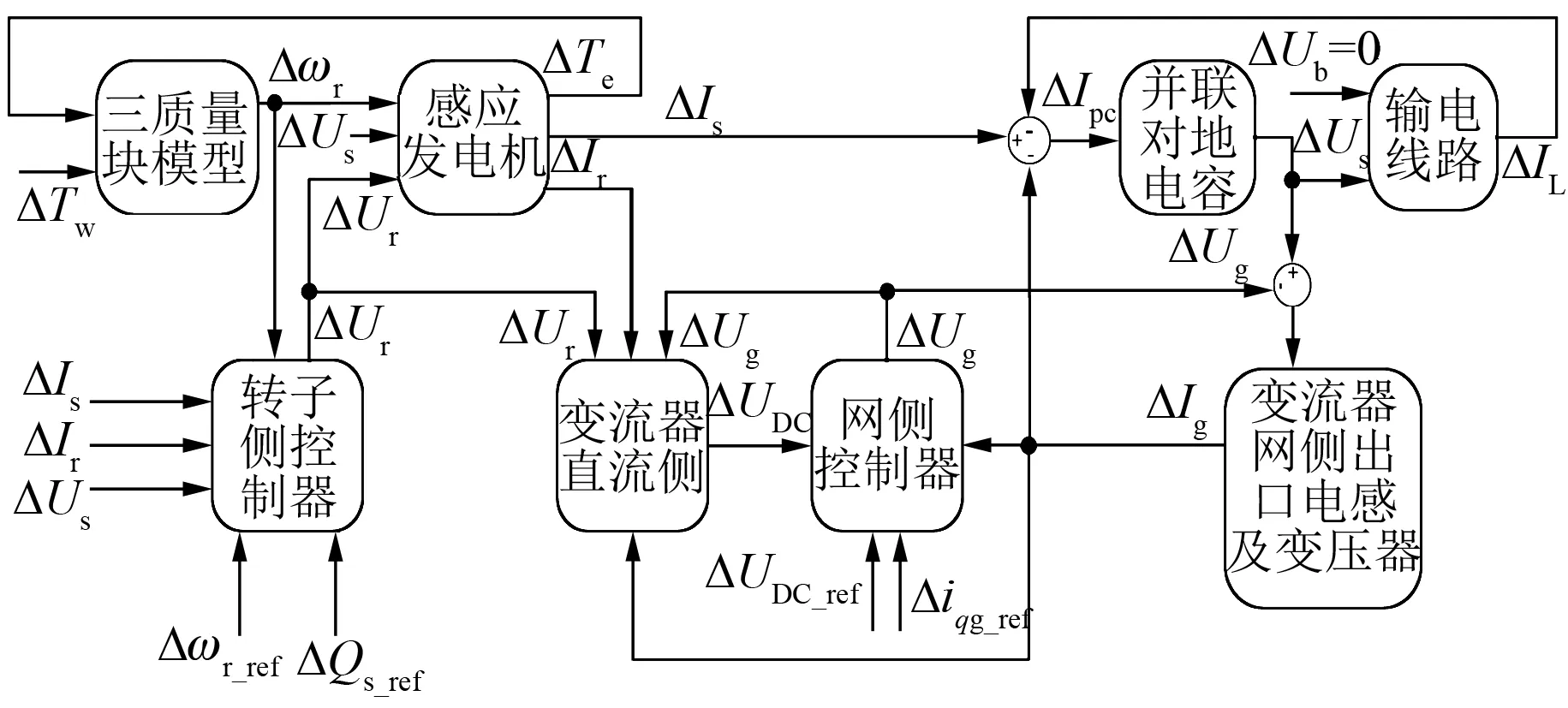
圖3 雙饋型風電機組連接至電力系統的小信號模型

圖3所示的雙饋風力發電機組小信號模型由軸系、感應發電機、轉子側控制器、變流器直流側、網側控制器、變流器出口電感及變壓器、并聯補償電容和輸電線路共計8個模塊構成。其中:軸系模塊以風力轉矩ΔTω和發電機電磁轉矩ΔTe作為輸入變量，以高速軸角速度，即發電機角速度Δωr為輸出變量；感應發電機模塊以發電機角速度Δωr、定子電壓ΔUs和轉子電壓ΔUr作為輸入變量，以發電機電磁轉矩ΔTe、定子輸出電流ΔIs和轉子輸出電流ΔIr為輸出變量；網側控制器模塊以發電機角速度Δωr、發電機角速度參考值Δωr_ref、定子無功參考值ΔQs_ref、轉子輸出電流ΔIr、定子輸出電流ΔIs和定子電壓ΔUs作為輸入變量，以轉子電壓ΔUr為輸出變量；變流器直流側模塊以轉子電壓ΔUr、轉子輸出電流ΔIr、網側變流器電壓ΔUg和網側變流器輸出電流ΔIg為輸入變量，以電容兩端直流電壓ΔUDC為輸出變量；網側控制器模塊以直流電壓ΔUDC、直流電壓參考值ΔUDC_ref、網側變流器輸出電流參考值Δiqg_ref和網側變流器輸出電流ΔIg為輸入變量，以網側變流器電壓ΔUg為輸出變量；變流器出口電感及變壓器模塊以定子電壓ΔUs和網側變流器電壓ΔUg為輸入變量，以網側變流器輸出電流ΔIg為輸出變量；并聯補償電容模塊以網側變流器輸出電流ΔIg、線路電流ΔIL、定子輸出電流ΔIs為輸入變量，以定子電壓ΔUs為輸出變量；輸電線路模塊以定子電壓ΔUs和電網電壓ΔUb為輸入變量，以線路電流ΔIL為輸出變量。

上述小信號模型對應的狀態方程可表示為

其中狀態變量

ΔX=

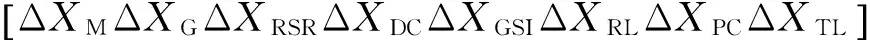
[Δθturb, Δθgear, Δθr, Δωturb, Δωgear, Δωr, Δψqs,

Δψds, Δψqr, Δψdr, Δx0, Δx1, Δx2, Δx3, Δx4,

ΔUDC, Δx5, Δx6, Δx7, Δigx, Δigy, Δupc,x,Δupc,y,

ΔiLx,ΔiLy,Δusc,x,Δusc,y]T

式中：θturb、θgear、θr——葉片、低速軸和高速軸扭矩角；

ωturb、ωgear、ωr——各部分轉速；

ψqs、ψds、ψqr、ψdr——發電機定轉子磁鏈的q軸和d軸分量；

x0、x1、x2、x3、x4、x5、x6、x7——變流器控制變量；

UDC——直流電容電壓；

igx、igy——網側變流器輸出電流的x和y軸分量；

upc,x、Δupc,y——變壓器出口并補電容電壓的x和y軸分量；

iLx、iLy、usc,x、usc,y——輸電線路電流和串補電容兩端電流的x和y軸分量。

輸入變量：

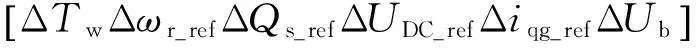
對應的狀態矩陣

2 雙饋型風力發電系統小信號模型特征值

該雙饋型風電機組連接至電網的小信號模型共有27個狀態變量，分別是：

ΔX=[ΔiLx, ΔiLy, Δusc, x, Δusc, y, Δupc, x,

Δupc, y, Δψqs, Δψds, Δψqr, Δψdr, Δx3,

Δθturb, Δθgear, Δθr, Δωturb, Δωgear, Δωr, Δx4,

Δx5, ΔUDC, Δx6, Δigx, Δigy,

在MATLAB/Simulink搭建小信號模型，變流器控制參數如表1所示。對系統進行特征值分析，系統所有的振蕩模態如表2所示。

表1 雙饋型風電機組變流器控制PI參數

表2列出的所有27個特征值中：有9對共軛的情況出現，即產生9種振蕩模態；其余9個特征值虛部均為零，表現為非振蕩模態，僅對其他9個振蕩模態進行詳細分析。為了確定與各振蕩模態相關度較高的狀態變量，計算9個振蕩模態關于各狀態變量的相關因子，如表3所示。對各個振蕩模態影響較大的相關因子在表3中加黑標出。

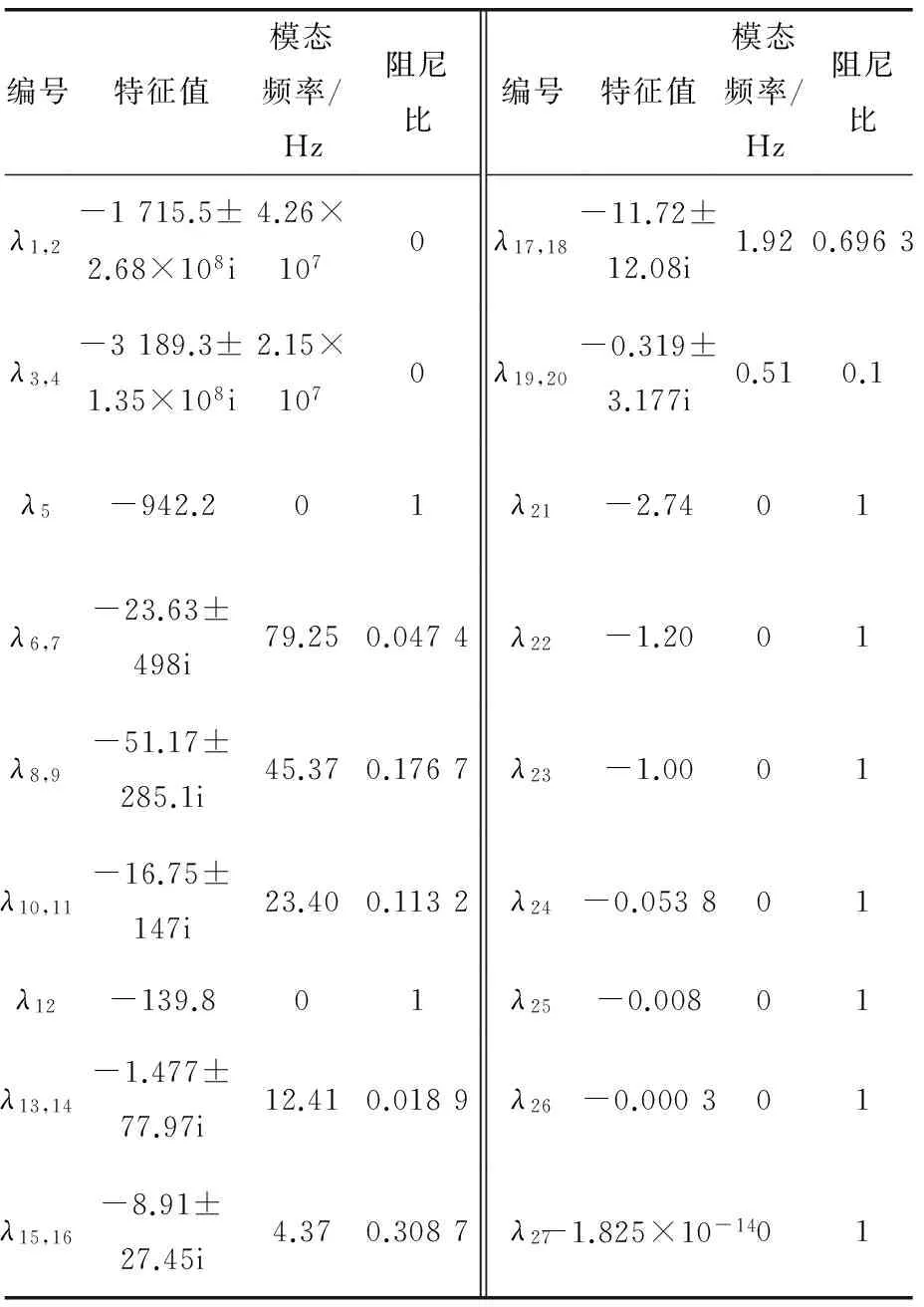
表2 雙饋型風電機組連接至電力系統的小信號模型特征值

系統共存在電氣諧振、SSR、SSO、SSCI和低頻振蕩五種振蕩模態，各種振蕩模態詳細信息如表4所示。

3 雙饋型風力發電系統機網振蕩模態的物理模型驗證

針對搭建的小信號模型，采用電壓波動、功率波動等小擾動方式激發振蕩，使用Simulink的FFT分析工具，驗證與上述分析對應的全部機網相互作用模態，如圖4所示。

(1) 電氣諧振模態。λ8,9對應的振蕩模態主要受網側變流器輸出電抗作用，分析流經網側變流器輸出電抗Lg的電流波形，得到其對應頻譜特性如圖4(a)所示。網側變流器輸出電流中，在基頻附近含有大量的45 Hz左右的諧波成分，這與λ8,9對應的45.37 Hz的振蕩頻率相吻合。

(2) 次同步諧振。λ6,7和λ10,11對應的振蕩模態與輸電線路電流和串補電容的端電壓有很強的作用，考慮時域模型中的輸電線路電流和定子輸出電流對應的諧波成分。由于輸電線上的電流諧波成分較小，對定子輸出電流進行頻譜分析，如圖4(b)所示。定子輸出電流除50 Hz基頻成分外，還含有20 Hz和80 Hz諧波成分，這與λ10,11和λ6,7兩種振蕩模態分別對應的23.40 Hz和79.25 Hz的次同步諧振頻率和超同步諧振頻率相吻合。

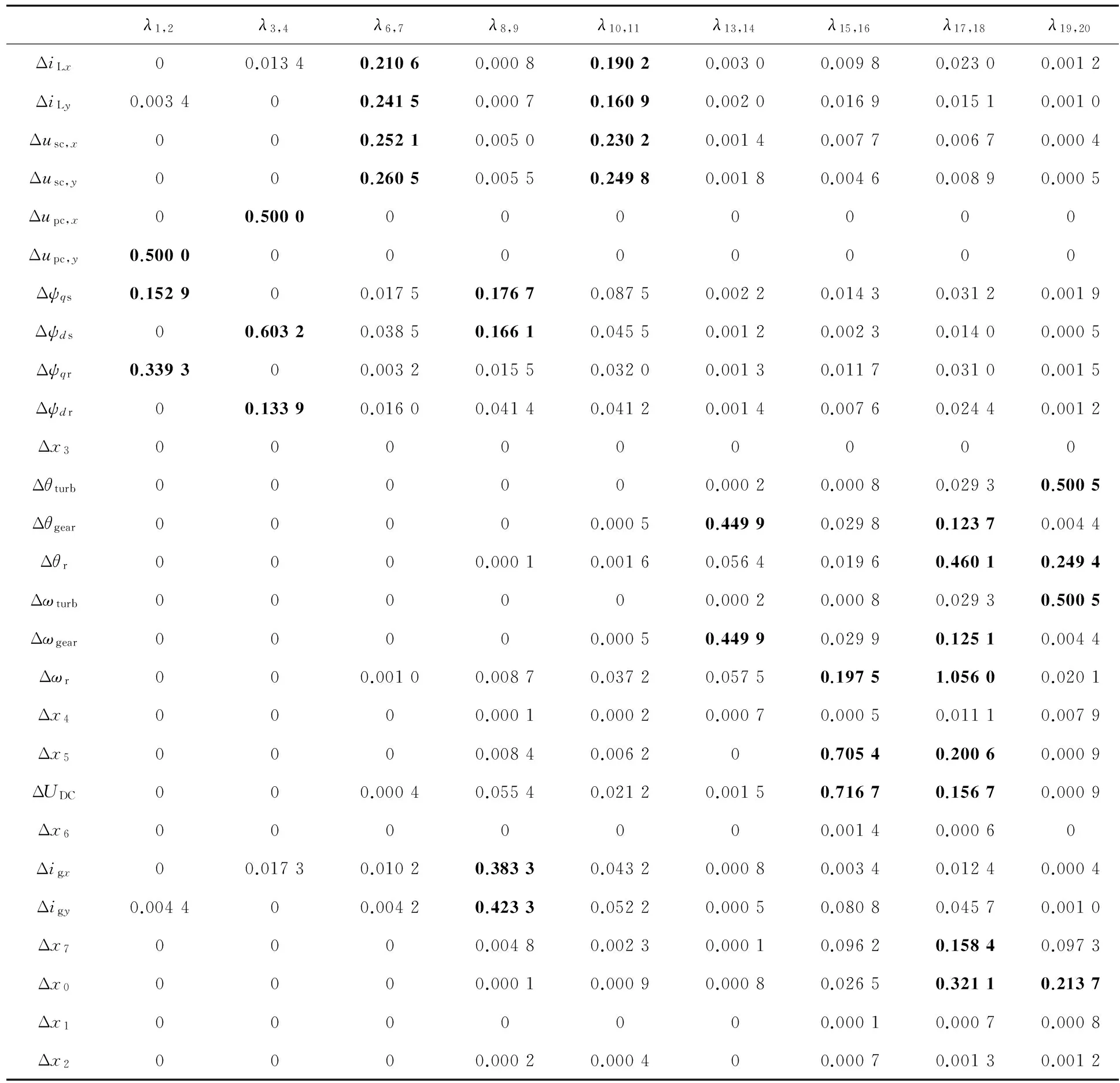
表3 雙饋型風電機組相關因子表

表4 雙饋型風電機組連接至無窮大電網的各種振蕩模態

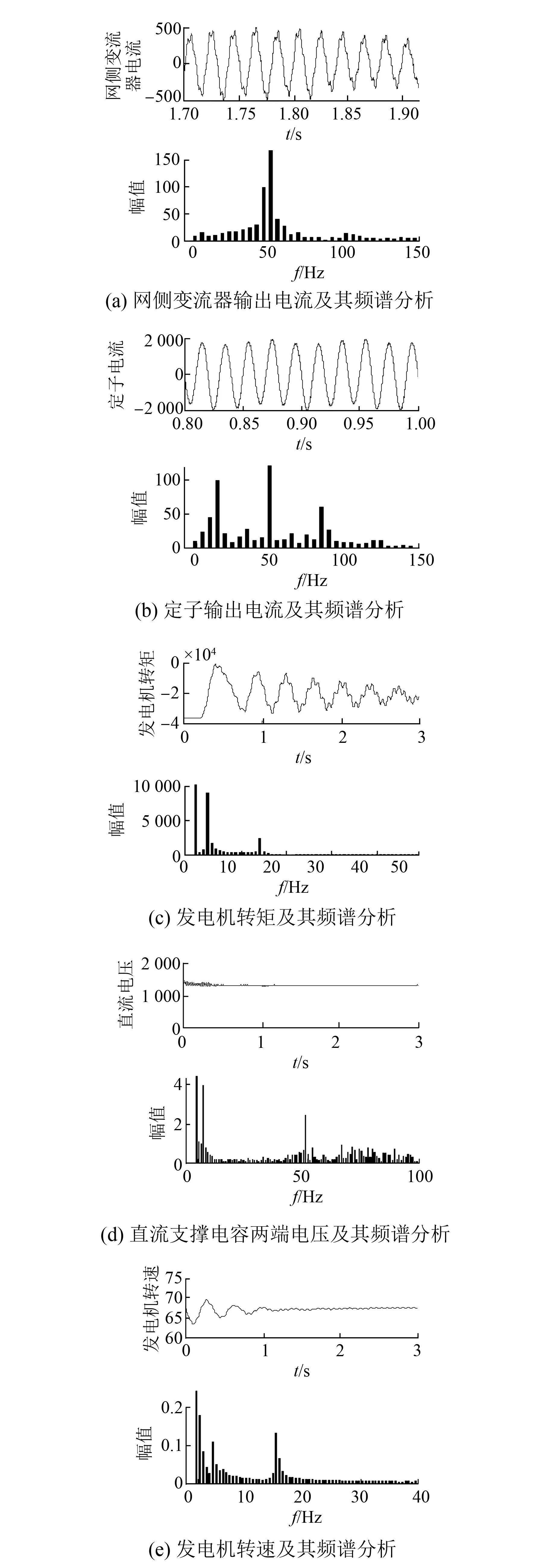
圖4 時域仿真波形及其頻譜分析

(3) 次同步振蕩。λ13,14和λ17,18對應的振蕩模態受齒輪箱的扭轉角和轉速以及發電機的轉子扭轉角和轉速影響較大。分析發電機和低速軸轉矩，對應的轉矩波形和頻譜分析如圖4(c)所示。發電機轉矩含有2.5 Hz和14 Hz附近的諧波成分，這與λ17,18和λ13,14兩種振蕩模態分別對應的1.92 Hz和12.41 Hz的軸系振蕩頻率相吻合。

(4)次同步控制相互作用模態。λ15,16對應的振蕩模態受網側變頻器影響較大，其中直流電容電壓調整相關變量Δx5和直流側電容電壓ΔUDC相關因子均超過0.7，分析直流電容兩端電壓，對應的電壓波形和頻譜特性如圖4(d)所示。變流器中的直流支撐電容兩端電壓除了與系統頻率相關的50 Hz諧波外，還含有約4 Hz的諧波成分，這和λ15,16對應的與次同步控制相關的4.37 Hz的振蕩頻率相吻合。

(5)低頻振蕩模態。λ19,20對應的振蕩模態受機械軸系影響較大，分析發電機轉速的頻譜特性如圖4(e)所示。發電機轉速中含有顯著的低頻諧波成分，主要集中在0.5 Hz附近，這與λ19,20對應的0.51 Hz的低頻振蕩頻率相吻合。此外，由圖4(e)還可以看出，本次小干擾還同時在發電機轉速中激發出2.5 Hz和14 Hz附近的諧波成分，這與λ17,18和λ13,14兩種振蕩模態對應的1.92 Hz和12.41 Hz的軸系振蕩頻率相吻合。

4 各個振蕩模態的最佳PI參數選取

分析表3可知，與變流器控制PI參數緊密相關的有SSO、SSCI和低頻振蕩三種振蕩模態。忽略對系統各振蕩模態均無影響的PI參數，僅分析對系統振蕩模態有影響的PI參數的變化趨勢。

為了研究Kp0的變化對系統各個振蕩模態的影響，保持其他變量不變，Kp0以30的步長從30變化到3 000，得到系統各種振蕩模態下所對應的特征值的實部和阻尼比的變化，如圖5所示。其中橫軸為特征值對應的實部，縱軸為對應的阻尼比，箭頭表示隨Kp0的增大特征值的變化趨勢，不受該參數影響的特征值沒有給出。

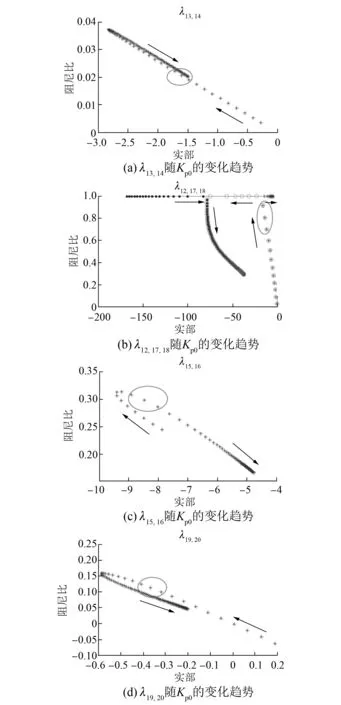
圖5 各振蕩模態隨Kp0的變化趨勢

由圖5(a)可見，在Kp0變化的過程中，λ13,14對應的振蕩模態的特征值實部始終為負，且其絕對值隨Kp0的增大先變大后變小，相應的阻尼比也有同樣的變化趨勢，在Kp0為960～990時，阻尼比達到最大值0.037 2。因此，考慮該振蕩模態的變化特性，Kp0的最佳范圍為960～990。

由圖5(b)可見，在Kp0變化的過程中，λ12,17,18對應的振蕩模態的特征值實部始終為負，且該振蕩模態經歷了先衰減消失后又出現且振蕩加劇的現象。在Kp0從30增大至360的過程中，λ12對應的是非振蕩模態，且特征值絕對值逐漸減小，λ17,18對應的振蕩模態，特征值實部絕對值和阻尼比均逐漸增大；當Kp0達到390時，λ17,18對應的振蕩模態變為兩個非振蕩模態；Kp0從390增大至540的過程中，λ17對應的特征值實部絕對值逐漸增大，而λ18對應的特征值實部絕對值逐漸減小；當Kp0達到570時，λ12和λ17這兩個非振蕩模態合為一新的振蕩模態，且隨著Kp0的繼續增大，新的振蕩模態的特征值實部絕對值和阻尼比均不斷減小，而λ18對應的特征值實部絕對值仍舊不斷減小。因此，考慮到λ12,17,18對應的振蕩模態的變化特性，Kp0的最佳范圍為330～360。

由圖5(c)可見，在Kp0變化的過程中，λ15,16對應的振蕩模態的特征值實部始終為負，且其絕對值隨Kp0的增大先增大后減小，相應的阻尼比也有同樣的變化趨勢，在Kp0為210～330時，阻尼比達到最大值0.313 8。因此，考慮該振蕩模態的變化特性，Kp0的最佳范圍為210～330。

由圖5(d)可見，在Kp0變化的過程中，λ19,20對應的振蕩模態的特征值實部先為正后為負，從Kp0大于150之后，特征值實部始終為負，且其絕對值隨Kp0的增大先變大后變小，相應的阻尼比也有同樣的變化趨勢，在Kp0為480～720時，阻尼比達到最大值0.159 5。因此，考慮該振蕩模態的變化特性，Kp0的最佳范圍為480～720。

考慮各個振蕩模態的阻尼比變化特性，系統最佳Kp0如表5所示。可得系統最佳的Kp0范圍為300～360，相應的各個振蕩模態運行范圍如圖5中橢圓虛線所示。

Ki0、Kp1、Kp3、Kp4、Kp5、Ki5、Kp6、Kp7對系統振蕩模態的研究過程與Kp0一樣。

根據上述不同PI參數對各個振蕩模態的影響，選取最佳PI參數，如表6所示。利用表6給出的PI參數對雙饋型風電機組振蕩模態進行分析，各種振蕩模態詳細信息如表7所示。

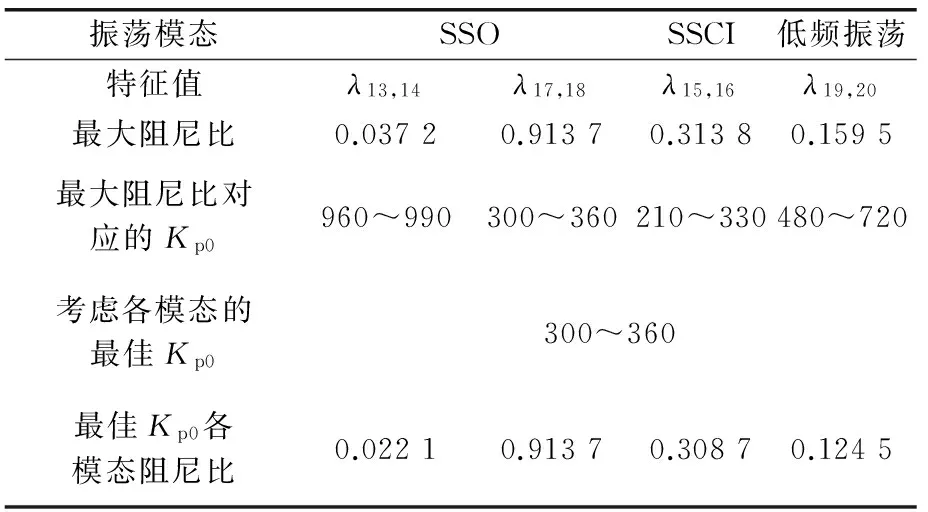
表5 Kp0的改變對各個振蕩模態阻尼比的影響

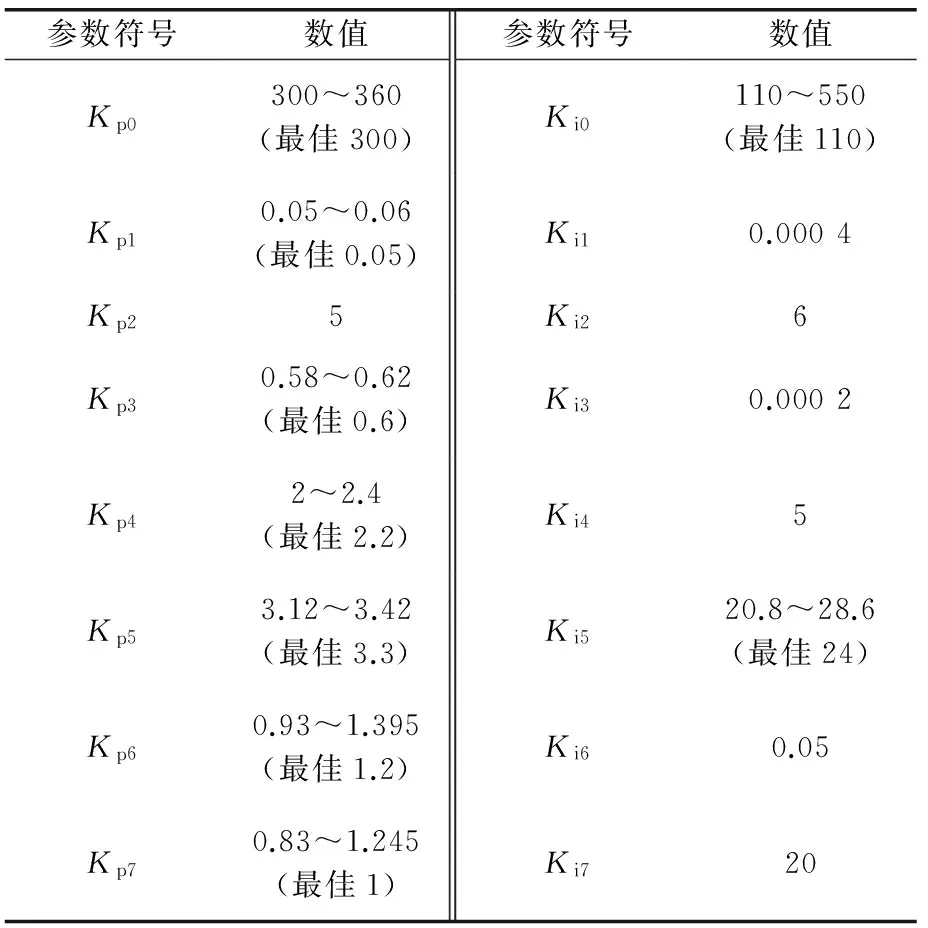
表6 雙饋型風電機組變流器控制最佳PI參數

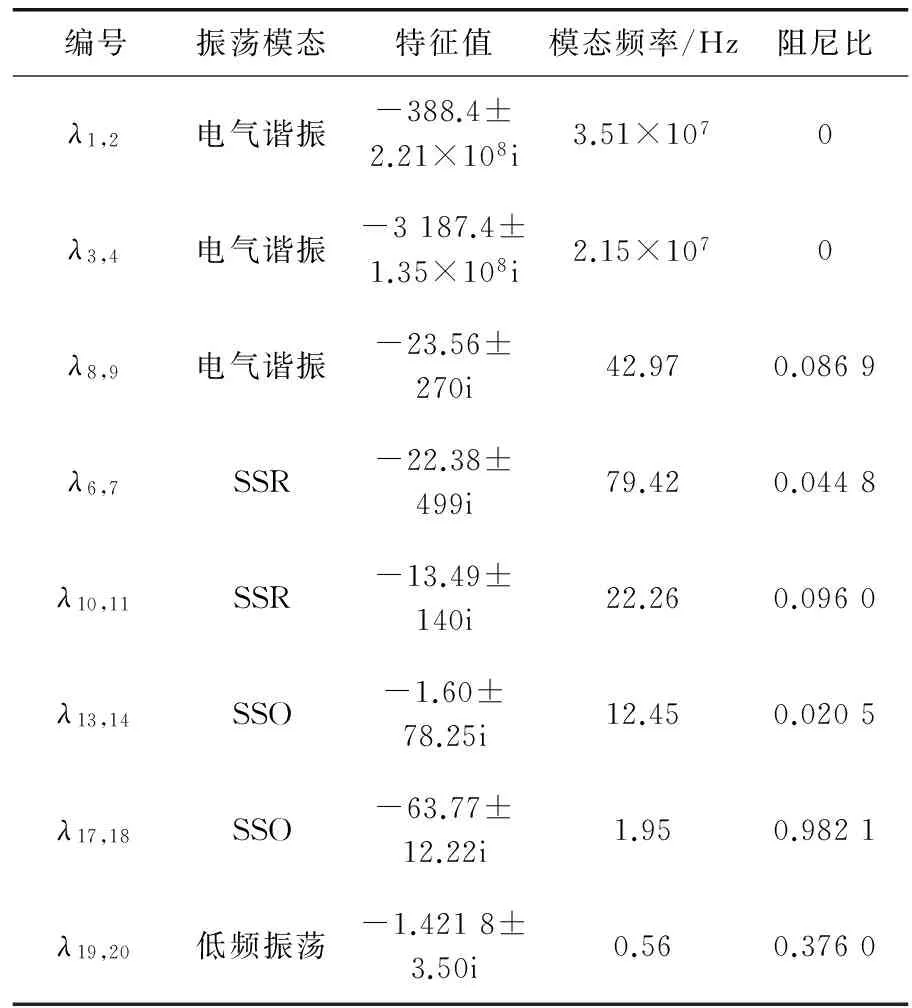
表7 雙饋型風電機組變流器控制最佳PI參數對應的各種振蕩模態

表7表明，系統共出現8種振蕩模態，與表2相比，λ15,16對應的SSCI振蕩模態消失了。這說明，通過合理的變流器控制PI參數調節可以起到減弱甚至消除SSCI振蕩模態。另外，λ13,14對應的阻尼比由0.018 9增大為0.020 5，λ17,18對應的阻尼比由0.696 3增大為0.982 1，λ19,20對應的阻尼比由0.1增大為0.376 0，因此，可通過優化變流器控制PI參數增大次同步振蕩模態和低頻振蕩模態對應的阻尼比，起到減弱軸系振蕩和低頻振蕩的目的。

5 針對最佳PI參數的物理模型驗證

上述小信號模型表明，通過對變流器控制PI參數進行優化，可以消除系統次同步控制相互作用，減弱系統次同步振蕩和低頻振蕩。為了驗證該小信號模型的仿真結果，通過MATLAB/Simulink搭建時域模型進行仿真驗證。

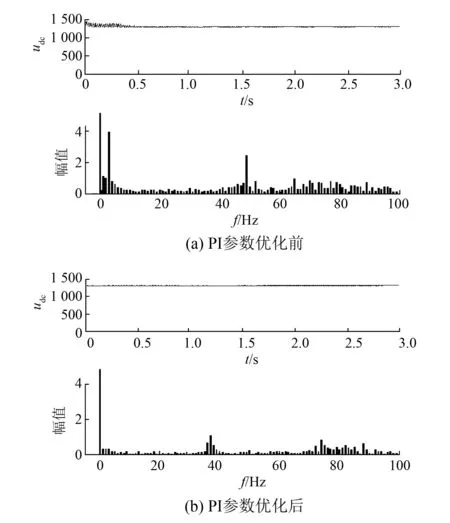
圖6 直流電壓波形及FFT分析

圖6為變流器控制參數優化前后直流電容兩端電壓波形及其FFT分析。圖6(a)表明，在原始變流器控制參數作用下，直流電壓中含有4.5 Hz左右的諧波成分，該諧波成分與小信號模型中的SSCI振蕩模態相對應。圖6(b)的FFT分析結果表明，通過變流器控制參數的優化，該諧波成分被消除，這表明通過變流器控制參數的優化，可以達到削弱甚至消除SSCI振蕩模態的效果。

圖7為變流器控制參數優化前后發電機轉矩波形及其FFT分析。圖7(a)表明，在原始變流器控制參數作用下，發電機轉矩波形中含有3 Hz和14 Hz左右的諧波成分。這兩種諧波成分與小信號模型中的SSO模態相對應。圖7(b)的FFT分析結果表明，通過變流器控制參數的優化。這兩種諧波對應的幅值均有所下降，發電機轉矩的振蕩幅度也有所減弱。這表明通過變流器控制參數的優化，可以達到削弱SSO的效果。

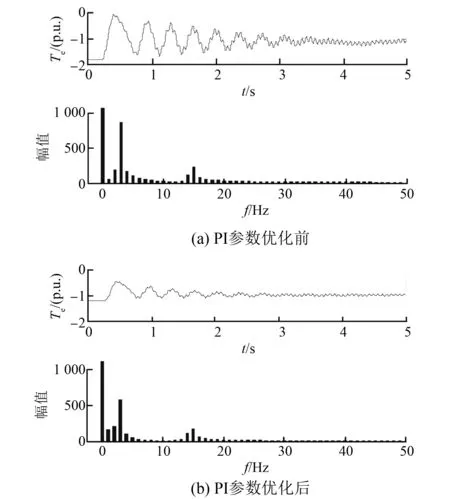
圖7 發電機轉矩波形及FFT分析

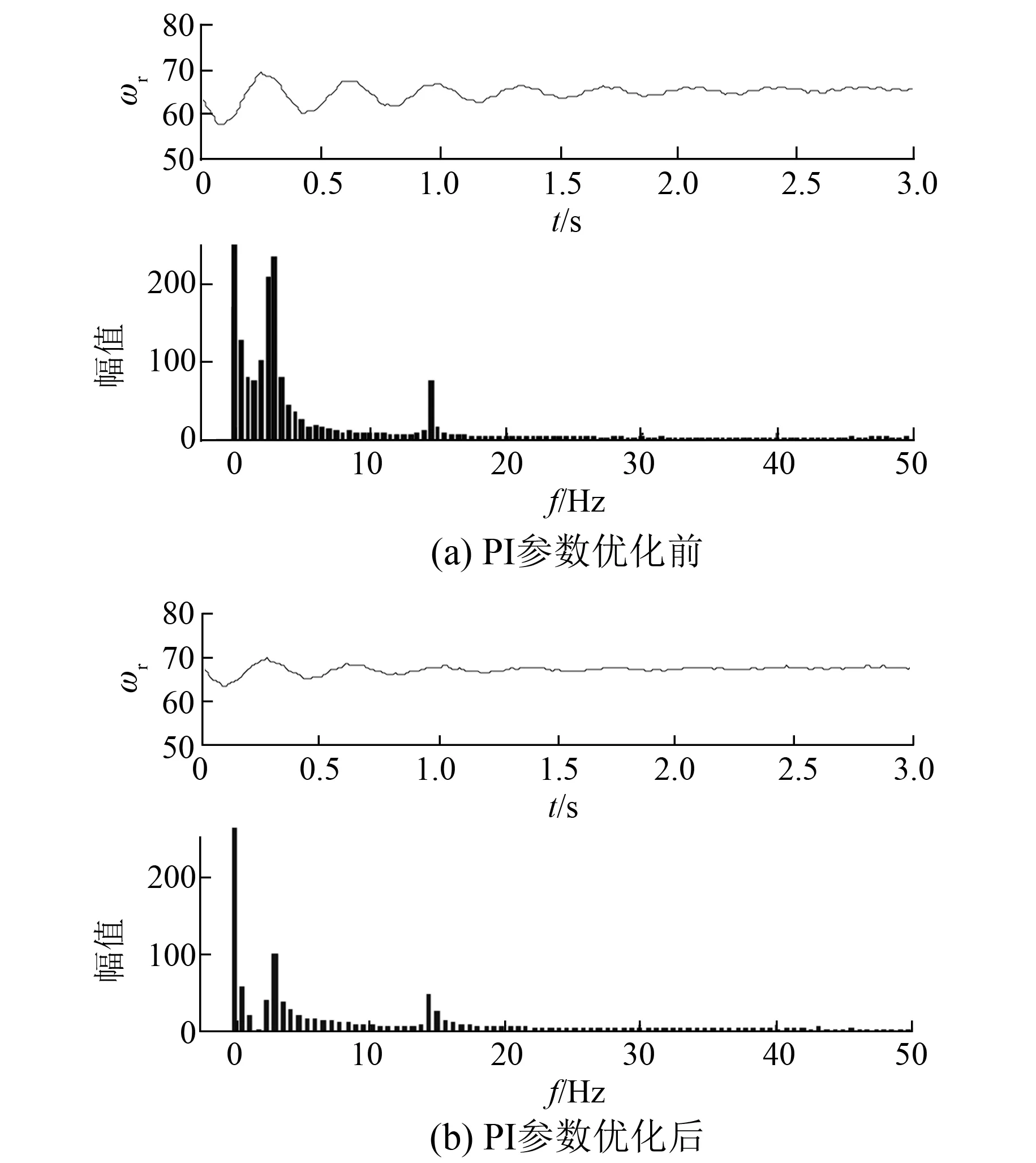
圖8 發電機轉速波形及FFT分析

圖8為變流器控制參數優化前后發電機轉速波形及其FFT分析。圖8(a)表明，在原始變流器控制參數作用下，發電機轉速波形中含有0.5 Hz、3 Hz和14 Hz左右的諧波成分，其中0.5 Hz諧波成分與小信號模型中的低頻振蕩模態相對應，后兩種諧波成分與小信號模型中的SSO模態相對應。圖8(b)中的FFT分析結果表明，通過變流器控制參數的優化，這三種諧波對應的幅值均有所下降，發電機轉矩的振蕩模型也有所減弱。這表明通過變流器控制參數的優化，可以達到削弱低頻振蕩和SSO的效果。

6 結 語

雙饋型風力發電的機網統一系統，可通過合理控制參數，改變振蕩組態阻尼比的大小，可實現對振蕩的抑制作用。本文主要完成以下工作：

(1) 建立了雙饋型風力發電系統的機網統一模型，分析出系統所有的特征值。

(2) 建立相關因子表，分析了與振蕩模態對應的狀態變量，通過時域仿真驗證全部模態的存在性。

(3) 研究了變流器控制參數變化對阻尼比的影響，尋找出全功率情況下的一組控制參數，通過理論分析和時域結合的方式研究控制參數對振蕩模態的影響。

本文分析論證了雙饋型風力發電系統變流器控制參數對系統的振蕩模態具有抑制作用，對風電場的安全和穩定運行有重大的意義。

[1] 何世恩,董新洲.大規模風電機組脫網原因分析及對策[J].電力系統保護與控制,2012,40(1):131-137.

[2] 孫華東,張振宇,林偉芳,等.2011年西北電網風機脫網事故分析及啟示[J].電網技術,2012,36(10):76-80.

[3] 董飛飛,劉滌塵,廖清芬,等.基于阻尼正弦原子分解的次同步振蕩模態辨識[J].中國電機工程學報,2013,33(19):119-125.

[4] 李輝,陳耀君,趙斌,等.雙饋風電場抑制系統次同步振蕩分析及控制策略[J].中國電機工程學報,2015,35(7):1613-1620.

[5] 吳熙,蔣平,胡弢.電力系統穩定器對次同步振蕩的影響及其機制研究[J].中國電機工程學報,2011,31(22):56-63.

[6] 趙欣,高山,張寧宇.SVC接入位置對次同步振蕩的影響機理與SVC控制策略研究[J].中國電機工程學報,2013,33(25):107-114.

[7] 王冠青,孫海順,朱鑫要,等.STATCOM附加電壓控制抑制次同步諧振的理論和仿真[J].電力系統自動化,2013,37(11):33-38.

[8] 董曉亮,謝小榮,韓英鐸,等.基于定轉子轉矩分析法的雙饋風機次同步諧振機理研究[J].中國電機工程學報,2015,35(19):4861-4869.

[9] 李志鵬,謝小榮.應用靜止同步補償器抑制次同步諧振的模態互補電流控制方法[J].中國電機工程學報,2010,30(34):22-27.

[10] 張劍,肖湘寧,高本鋒,等.雙饋風力發電機的次同步控制相互作用機理與特性研究[J].電工技術學報,2013,28(12):142-149.

[11] 陳婧華.雙饋風電場經串補并網引起的次同步振蕩分析與抑制[D].北京:華北電力大學,2015.

[12] SURIYAARACHCHI D H R, ANNAKKAGE U D, KARAWITA C, et al. A procedure to study sub-synchronous interactions in wind integrated power systems[J].IEEE Transactions on Power Systems,2013,28(1):377-384.

[13] 李輝,陳宏文,楊超,等.含雙饋風電場的電力系統低頻振蕩模態分析[J].中國電機工程學報,2013,33(28):17-24.

[14] 楊黎暉,馬西奎.雙饋風電機組對電力系統低頻振蕩特性的影響[J].中國電機工程學報,2011,31(10):19-25.

[15] 王瑞琳.風力發電機與電網之間扭振相互作用的研究[D].上海:上海交通大學,2012.

Analysis of Influence of Doubly Fed Wind Power System PI Converter Control Parameter on Oscillation Mode

WU Wangping, XIE Da, ZHAO Zuyi, LU Yupu, CHU Haoxiang

(School of Electronic Information and Electrical Engineering, Shanghai Jiaotong University,Shanghai 200240, China)

The effects of converter control parameters of DFIG wind generation system on the oscillation modes were studied. A complete small signal model in MATLAB/Simulink was proposed. By using eigenvalue and participation factors analysis, the oscillation modes were discovered and classified. By altering the parameters of converter, the changes of oscillation modes were studied. Finally, simulation was done on the MATLAB/Simulink. The research showed that the oscillation could be suppressed by optimizing the control parameters of converter.

wind farm; converter; doubly fed induction generator; oscillation mode

國家自然科學基金項目(51277119)

吳汪平(1991—)，男，碩士研究生，研究方向為電力系統及其自動化。 解 大(1969—)，男，博士研究生，副教授，研究方向為電力系統分析、靈活交流輸電設備、新能源。 趙祖熠(1991—)，男，碩士研究生，研究方向為電力系統及其自動化。 魯玉普(1991—)，男，碩士研究生，研究方向為新能源并網技術和風力發電系統機網扭振。 楚皓翔(1990—)，男，碩士研究生，研究方向為電力系統及其自動化。

TM 315

A

1673-6540(2017)07- 0098- 10

2016 -11 -21