基于上證指數高頻數據的中國資本市場微觀特性研究?

唐振鵬1)2)3) 陳尾虹1)? 冉夢1)

1)(福州大學經濟與管理學院,福州 350116)

2)(福建省金融科技創新重點實驗室,福州 350116)

3)(福建省企業發展研究中心,福州 350116)

基于上證指數高頻數據的中國資本市場微觀特性研究?

唐振鵬1)2)3) 陳尾虹1)? 冉夢1)

1)(福州大學經濟與管理學院,福州 350116)

2)(福建省金融科技創新重點實驗室,福州 350116)

3)(福建省企業發展研究中心,福州 350116)

(2017年1月6日收到;2017年4月6日收到修改稿)

以上證指數高頻數據為研究對象,基于上漲、平緩和下跌三個市場狀態分析我國金融市場的微觀特性.通過分析上證指數在不同時間間隔下的概率分布、自相關性和多分形三個特性,發現上證指數對數增量序列存在厚尾、列維非高斯分布特征,且隨著時間間隔的增大,收益序列愈收斂于正態分布,其中,下降趨勢收斂于正態分布的速度更快,擬合于列維分布的效果更好.最為突出的是,在自相關函數分析中,上證指數的收益率無長期記憶性,而波動率則具有較強的記憶性.同時,波動率的自相關性存在明顯的周期性特征,即T=240 min,且在下降趨勢時其相關性最高.在以時間增量刻畫的多重分形結構中,對于不同的時間序列、時間間隔,由于受投資期限和流動性的影響,三種股市狀態的收益率波動存在著短期和長期性的差異.上證指數的總體宏觀行為與國際成熟股市較為一致,但在微觀特性上仍存在顯著差異,其所特有的周期性是投資者的慣性反沖所致,而自相關性函數較之成熟股市衰減較慢,則表明投資者的投資行為更多地受歷史信息的影響.

資本市場,微觀特性,上證指數,高頻數據

1 引 言

1995年,Mantegna和Stanley[1]在《Nature》發表了關于經濟指數標度行為的研究成果,這一開創性的工作拉開了金融物理學研究的帷幕,吸引了眾多物理學家加入到相關研究中.近年來,經濟學家同樣將統計物理學的概念和方法引入金融、經濟、交通物流和社會財富等系列問題的研究中[2?5],金融物理學作為一門新的交叉學科應運而生,其中最為系統和深入的研究集中于股票市場.這一方面是由于各個股票市場保存了大量的交易數據,特別是高頻和超高頻數據的發展為研究提供了足夠的數據深度;另一方面是不同于傳統金融學的研究視角,金融物理學旨在揭示股票市場的普適性、自組織結構等.經濟物理學家對西方發達國家主要股市的數據做了大量系統的分析和研究,發現了一系列重要的共性結果,即在股市錯綜復雜的漲跌趨勢中,存在一些普遍適用的統計規律[1,6].而在中國股票市場的研究中,Wei和Wang[7]將多分形分析運用到金融市場的波動率測度和預測領域,并提出基于多分形的波動率測度MFV(multifractal volatility).吳斌哲和馬紅孺[8]對上證指數的概率密度分布和自相關特性進行分析,發現上證高頻指數的負相關性效應和投機性特征.Gao等[9]將網絡理論應用于中國股市,研究揭示了中國股票市場的拓撲屬性以及上市公司間的交互影響關系.在國內外股票市場的對比研究中,Qiu等[10]的研究指出我國股市基本與國際成熟股市的統計行為趨同,但在某些關聯行為上表現出一些差異.Gao等[11]的研究則表明我國股票市場與發達金融市場均存在與多重分形標度相關的層級結構特征,但層級結構各異.

但上述研究忽視了股市普適性背后隱匿的差異性及其原理,同時未能區分上漲、平緩和下跌等不同股市狀態并對其微觀特性進行研究.而值得注意的問題是:當股票市場處于不同的市場狀態下,其概率分布、自相關性和多分形性等統計規律有何差異?經濟意義如何?當股市分別處于上漲、平緩和下跌趨勢時,投資者的決策有何行為動機和依據?識別不同股市狀態的微觀特性對投資決策有何指導意義?本文以上證指數1 min高頻數據為研究對象,類比文獻[8]的國際股市研究,對中國金融市場微觀特性進行分析,并嘗試解釋其中的差異,以期對投資決策提出有效的指導意見.

2 物理金融方法的理論基礎

2.1 概率分布函數

2.1.1 厚尾分布

早期的金融理論一直認為金融資產價格或者收益率滿足正態分布,而Mandelbrot[12]提出了平穩列維分布,并創造性地應用平穩帕累托(stable Paretian)定律描述證券市場價格收益率的尾部分布,研究發現在刻畫棉花價格波動的概率分布上,平穩帕累托分布比正態分布的擬合效果更好,這一發現徹底顛覆了傳統的布朗運動模型.具有胖尾特征的金融資產收益的概率分布被越來越多的學者所發現,學界一般以互補概率或對數分段來捕捉這一特性.本文引入互補概率的類似方法,即分階排序法來刻畫金融資產收益的胖尾分布,該法具有易于實現、不損失信息量和噪聲小的優點[13,14].

考慮變量x的n個觀察值,真實概率密度為f(x),則其互補概率分布為將這n個觀察值從大到小排序,得到

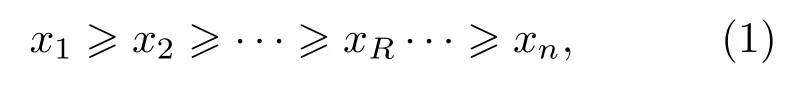
其中R為排名,即階.于是,nC(xR)是不小于xR的觀察值的數量,即

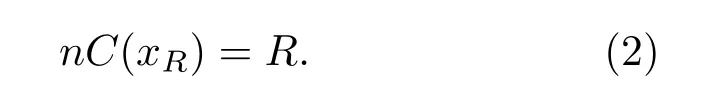
如若變量x具有冪律尾分布,即f(x)～x?(1+ω),那么C(x)～ x?ω,可得到xR與R之間的近似關系為

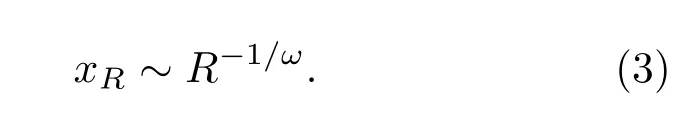
(3)式的精確表達式可從(2)式推導出,即

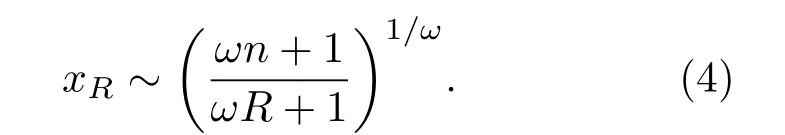
2.1.2 列維分布

大量的統計研究表明,股票指數對數增量的概率密度函數尾部胖于正態分布,同時又瘦于負冪律分布,因此,滿足截尾的列維(truncated Levy fl ight,TLF)分布[15?18],截尾從理論上保證了分布具有有限的二階矩,在靠近中心部分,TLF分布和列維分布并沒有明顯差別.為了簡化模型,進一步用列維分布對上證指數的對數增量分布進行處理.均值為零的列維分布的概率分布函數由下式給出

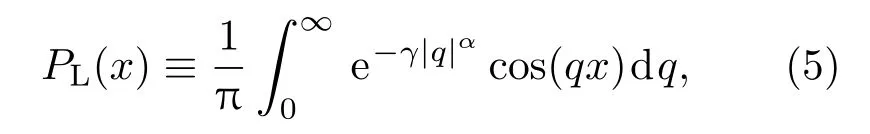
其中,x為隨機變量;α為一個標志分布特性的參數,且0<α 6 2;γ為一個正的標度因子.(5)式表示的列維平穩分布只在特殊情況下存在解析式,其中,當α=1/2,β=1時,對應的是列維-斯米爾洛夫分布;當α=1,β=0時,對應的是洛倫茲分布當α=2時,對應的是高斯分布,文中僅考慮具有零均值(μ=0)的對稱穩定分布(β=0),即具有指數α和尺度因子γ的對稱穩定分布.則對于任意股指對數增量Rk(t)=lnP(t+k)?lnP(t),其中,k為時間間隔,P(t)表示某一資產在時刻t的價格,并且Rk(t)滿足對稱的列維平穩分布

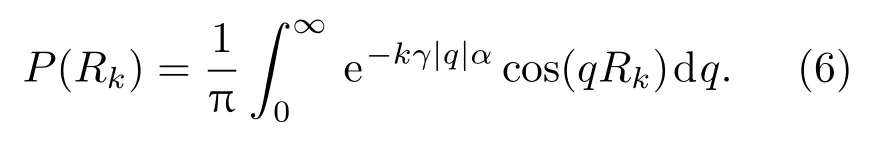
由于0對數增量處于概率分布的峰值且數據集中,同時考慮到計算的便利性,文中用列維分布擬合數據時,選擇P(R=0)(即對數增量的概率密度為0)的數據來求參數.如果分布具有自相似結構,則不同的k對應的α相同.列維平穩分布的重要特征之一是自相似性,則當Rk=0時,(6)式可以轉化為

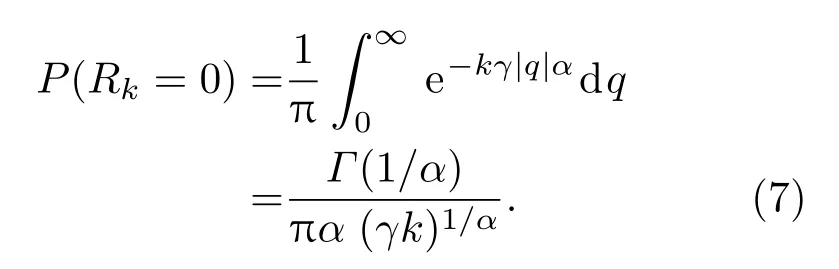
對等式兩邊取對數,得

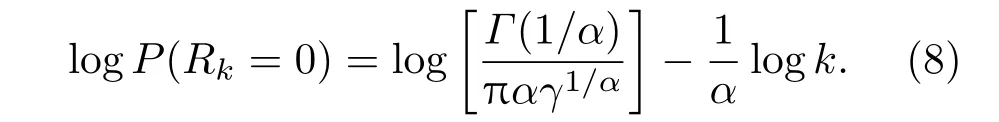
由(8)式擬合可得列維分布的指數分布參數α.

2.2 自相關函數

研究金融資產對數價格變化的兩兩獨立性,通常是分析對數價格時間變化的自相關函數或討論對數價格時間序列的頻譜密度.對于平穩隨機過程,研究這二類統計特性是等值的.對數價格變化的自相關函數是一個快速衰減的函數,刻畫它的相關時間通常小于一個交易日.因此,只有通過分析高頻數據才可以準確地估計序列的相關時間.自相關系數C(τ)定義為

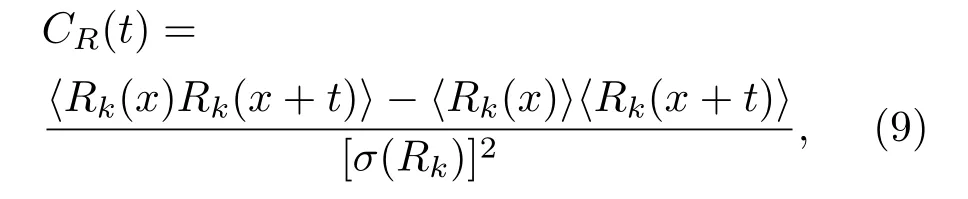
其中,在給定時間間隔k下,當t=0時,CR(t)=1.如果同一k水平下間隔為t的對數增量之間沒有關聯,即〈Rk(x)Rk(x+t)R= 〈Rk(x)R〈Rk(x+t)R,則CR(t)=0.

2.3 多分形

多分形是一種隨著時間標度t的增加,時間序列的動力學特征隨之變化的性質,即收益率的絕對矩隨著取樣間隔的不同呈現出冪律變化[19,20].Mandelbrot[21]對多分形過程的定義如下:X(t)=令X(t)為具有平穩增量δkX(t)的隨機過程,即δkX(t)=X(t)?X(t?k).假設對于所有的q∈Q存在,其中是包含間隔[0,1]的合適集,令進一步地,定義一個可微的函數,T是正實數值.

則標度不變性過程增量的絕對矩作為取樣間隔k的函數呈現冪律分布,那么我們可以稱過程X(t)是標度不變性.標度不變性過程分為兩種情況:當(q)是線性時比如(q)=qH(H為Hurst指數),該過程是單分形過程,這種情況下尺度可以擴展到一個無限制的尺度范圍(T=+∞).單分形過程就是所謂的自相似過程比如分形布朗運動或α-stable運動;當(q)為非線性時,該過程是多分形過程.非線性指數(q)是嚴格的凹函數.對于一個凹函數,其多分形性質不會對于任意大的標度都成立.通常我們定義T為整體尺度(integral scale),超過時間T該過程即停止呈現多分形特征.上述等式在k 6 T時成立.

3 數據和時間的選取

在處理股市數據的時間序列對價格的隨機動態進行分析與建模的過程中,時間尺度和價格尺度的選擇至關重要.關于時間尺度主要有3種不同的選擇:1)物理時間,該選擇無法對休市期間的信息與價格隨機動態特性建模;2)交易時間,即在開市期間流逝的時間,但這一選擇無法刻畫休市期間價格動態特性信息的時間效應;3)交易次數,即以每筆交易為時間單位,這種選擇下金融市場上觀測到時的一類隨機性就消失了,也即每筆交易間的時間間隔.目前,學者大量使用的是交易時間[6,8],為了研究結果的可比性,本文同樣選擇交易時間,即選用上證指數的1 min數據.通過周數據所得的漲跌趨勢圖(如圖1所示)將市場分為上漲、下跌和平緩振蕩三個狀態(如表1所列),本文將相對于前期低點漲幅超過30%的走勢定義為一個上漲趨勢,將相對于前期高點跌幅超過30%的走勢定義為一個下跌趨勢[22],并將變化幅度位于5%—10%的趨勢定義為一個平緩趨勢.同時,為剔除樣本量對研究結果的影響,將數據區間控制在同一時間長度,遇非交易日則日期順延.其中,上漲區間為2015年2月12日至2015年6月12日,平緩區間為2014年3月10日至2014年7月10日,下跌區間為2015年6月12日至2015年10月12日,采用的數據均來自于同花順數據庫(研究過程中曾試驗過多組不同的樣本數據,研究結論不變.考慮到篇幅問題以及時間的同步性,故選取2012年—2015年的樣本數據).

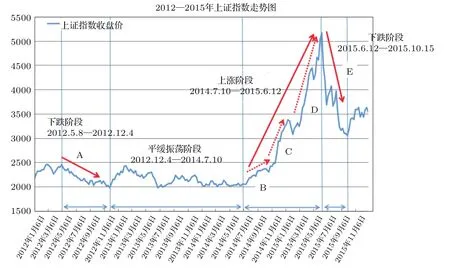
圖1 上證指數走勢Fig.1.Trend of Shanghai Stock Exchange composite index.

表1 上證指數市場狀態區間分布Table 1.Interval distribution of Shanghai Stock Exchange composite index in market state.

股票數據的價格尺度選擇也不惟一,根據研究目的的不同,可以區分為股指P(t),股指漲跌P(t+k)?P(t)等.本文考慮股指漲跌的統計特性,因此,選用股指的相對變化

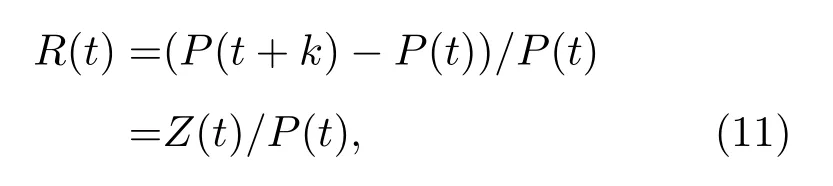
其中,k為時間間隔.作為統計量,股票價格是基于貨幣,指數的變化中也包含貨幣價值的變化,當k較小時,假定貨幣本身的波動在一段時間內變化不大,那么選擇R(t)作為統計量也就自然修正了貨幣波動的影響.但當k較大時,t+k和t則不對稱,從而導致對貨幣價值變化修正的偏離.注意到當k→0時,Z(t)實際上代表股指對數的變化.因此,更為合理的選擇是股指的對數增量,即

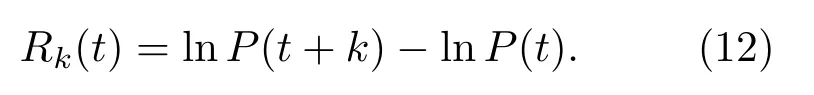
將Y定義為一個時間序列,則

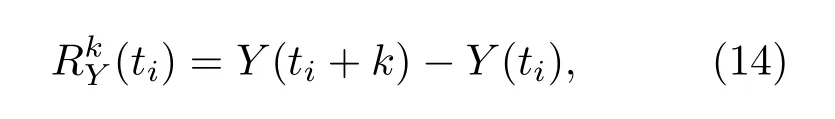
其中,Y=ln(P).作為統計變量,在下面的統計分析中,最小時間間隔k取為1 min,這一時間間隔既可較好地保持數據的連續性,亦可較好地處理指數變化時間序列間的短程相關性對數據統計特性分析的影響[23].則

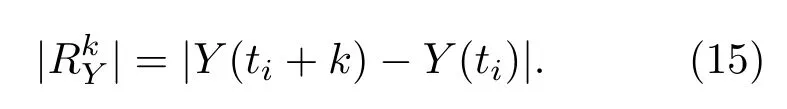
由(15)式可得標準化絕對收益:

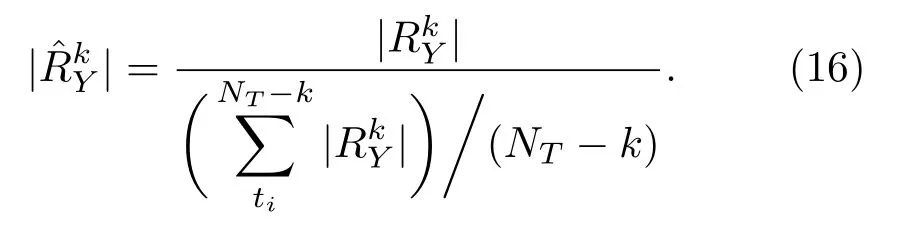
4 實證分析

4.1.1 厚尾分布

據介紹，水稻作為單子葉植物生物學研究的模式植物，在基因組與功能基因研究等方面具有重要作用。但與同為模式植物的擬南芥相比，水稻需要較大的室外大田或溫室，而且其較長的生長周期和對自然環境的高度依賴性，也制約了其生物學基礎研究的進一步發展，尤其是在水稻逆境抗性、水稻病原菌互作等方面。

為使不同時間間隔的序列具有可比性,以標準化絕對收益序列為研究樣本,分別取k=1 min和k=100 min.基于高頻數據對上證指數的上漲、平緩、下跌狀態進行微觀特性分析,互補概率分布如圖2所示.

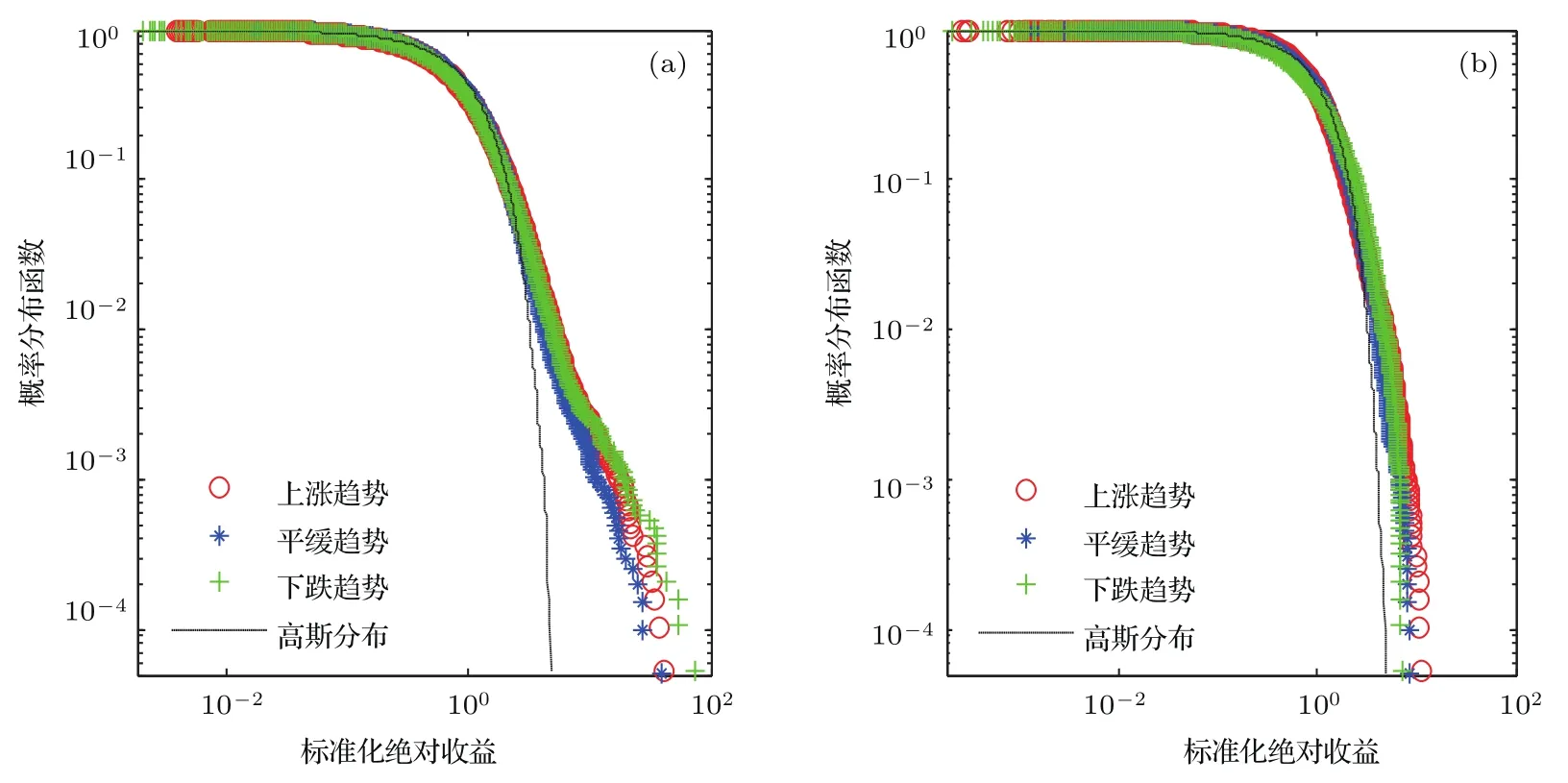
圖2 互補概率分布圖 (a)k=1 min;(b)k=100 minFig.2.Distribution of complementary probability with(a)k=1 min and(b)k=100 min.

從圖2可得,上證指數標準化絕對收益序列的分布函數呈現出厚尾特征,同時,Kolmogorov-Smirnov(KS)估計結果也表明三個階段的厚尾分布存在顯著性差異.但隨著時間間隔k由1 min增至100 min,收益序列的分布聚斂于正態分布.其主要原因是股票每分鐘的收盤價受到噪聲(短時間大量交易造成不連續)的影響,而隨著k的增加,可以濾掉噪聲,因此,k=100 min時的收益序列比k=1 min時更加收斂于正態分布.對比2組圖形可以看出,當k=1 min時,股市下跌趨勢的尾部分布比平緩、上漲趨勢更加擴散,而這一分布特征也符合股市信息沖擊的非對稱性,其主要是受政府對股市干預的宏觀政策、投資者掌握信息的不對稱性、股市缺乏做空機制和散戶投資者普遍具有從眾行為等因素的影響.投資者的行為決策深受投資者情緒的傳染,這種傳染效應在下跌期間尤甚.如2015年股災期間股票指數不斷下跌,投資者恐慌情緒迅速傳染,恐慌性拋售股票攀升,以致2016年初啟動熔斷機制后,股市多次觸碰熔斷而中斷.而當k=100 min時,下降趨勢的尾部分布較之平緩、上漲趨勢,則更擬合于正態分布,這主要是由于人本質上具有社會性,個人的投資決策易受社會因素的影響,因此,具有“恐慌”心理的投資者會加劇市場“恐慌”情緒的蔓延,我國股市在下降趨勢時存在較高的投資同質性,而較長時間間隔的收益序列則熨平了短期時間間隔內噪聲因素所帶來的發散特性.

而較之文獻[6]的研究,成熟股市的收益率在k=1 min時尾部呈現截尾現象,比我國股市的尾部分布更厚,我們認為這主要是由于我國股市有漲跌停限制,股票在一個交易日中的成交價格不能高于或低于限定的漲跌幅度,當超過該范圍時報價將視為無效,所以我國股市的振幅沒有國外股市那么劇烈.

4.1.2 列維分布

采用Mantegna-Stanley方法研究分布的最中心峰值即零收益的概率P(R=0)作為k的函數,這一方法可使我們只研究每一概率分布中受噪聲影響最少的點.首先分析Rk(t)的概率分布函數.分別取k=1,3,10,32,100,316,1000 min,求出不同市場狀態下對應的Rk(t)并統計其概率分布,即得到Rk(t)的概率分布函數.其次根據(8)式擬合得出列維分布的指數分布參數α,如圖3所示.

圖3是上證指數0對數增量的概率密度Pk(0)與k的雙對數圖,由圖可見數據點基本在一條直線上,表明列維分布假定是合理的.由最小二乘法進行數值擬合,可得上漲、平緩和下跌狀態下擬合直線的斜率(?1/α)分別為?0.6899,?0.5681,?0.5667,這一結果與標準普爾(S&P)指數的?0.71、歐元美元匯率的?0.71均存在差異,說明我國股市與成熟股市尚存在較大差距.同時,研究結果也與文獻[6]所得的0.65不同,這主要是由于本文考慮了股市的不同市場狀態.列維分布的指數分布參數α分別為1.4494,1.7604,1.7646,說明截斷列維飛行能夠描述尖峰胖尾特征,且具有緩慢漸近收斂到高斯域的特性.可知我國股市在下跌趨勢時(α=1.7646)更趨向于高斯分布(α=2).而擬合優度R2分別為0.9820,0.9866,0.9929,則進一步表明股市在下跌時列維分布的擬合效果更好,對于投資決策更具預測價值.

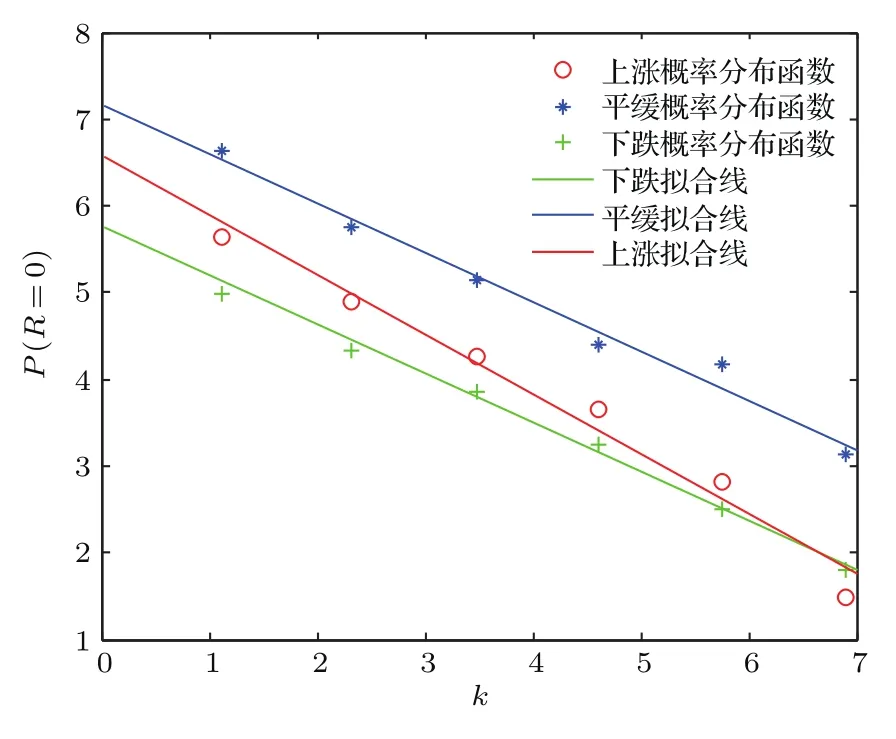
圖3 在上漲、平緩和下跌趨勢時P(R=0)與k的雙對數圖Fig.3.Situation in rising trend,steady trend and falling trend log-log plot of the probability P(R=0)versus k.

4.2 收益率Rk(t)與波動率的自相關性分析

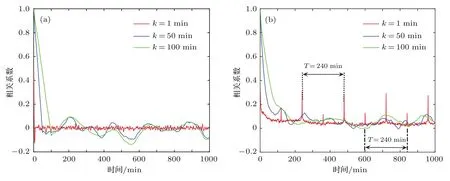
圖4 上漲趨勢情況 (a)收益率自相關函數;(b)波動率自相關函數Fig.4.Situation in rising trend:(a)Autocorrelation functions of the return;(b)autocorrelation functions of volatility.

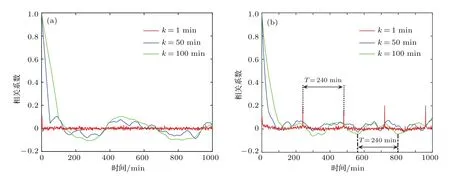
圖5 平緩趨勢情況 (a)收益率自相關函數;(b)波動率自相關函數Fig.5.Situation in steady trend:(a)Autocorrelation functions of the return;(b)autocorrelation functions of volatility.

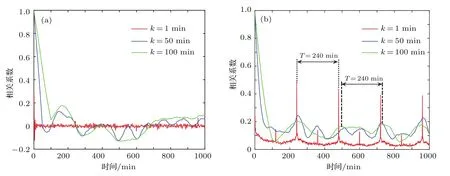
圖6 下跌趨勢情況 (a)收益率自相關函數;(b)波動率自相關函數Fig.6.Situation in falling trend:(a)Autocorrelation functions of the return;(b)autocorrelation functions of volatility.

從圖4—圖6可得,上漲、平緩和下跌趨勢波動率的自相關性均高于收益率的自相關性.當k=1時,收益率的自相關系數趨于0,這與傳統金融理論中的價格變動的獨立性假設一致.在非線性的時域關聯中,通常以收益率的絕對值,即波動率來考慮自相關性,并以它度量收益率漲落幅度的時間關聯.圖4(b)、圖5(b)、圖6(b)也證實了在較長的時間范圍內,k=1 min的自相關系數都不為0.在k=1,50,100 min時,收益率自相關性曲線的振幅均大于波動率自相關性曲線,k=1 min的曲線呈微弱式下降,k=50 min與k=100 min的曲線正負走勢則一致.

從圖4(b)上漲趨勢波動率自相關函數圖可得,在自相關函數的正負值特性中,當k=1 min時,自相關函數均為正值;當k=50 min時,自相關函數在t=530—537 min,t=786—796 min呈負相關;當k=100 min時,自相關函數在t=571—595 min,t=617 min呈負相關.在周期性特性中,當k=1 min時,在滯后期t=120 min,相關性系數趨于0.17,并以T=240 min的周期出現;在滯后期t=240 min,相關性系數趨于0.31,并以T=240 min的周期出現,即波動率曲線以T=120 min的周期呈現出低相關性和高相關性的交替變換.而這一周期性規律在k=100 min時依然不變.

從圖5(b)可得,在平緩趨勢時,k=1,50,100 min的波動率自相關系數均出現負值.在周期性特性中,當k=1 min時,在滯后期t=240 min,相關性曲線向上跳躍,以趨于0.2的值并以T=240 min的周期規律性地出現,且在k=100 min時這一周期性規律依然存在.在滯后期t=240,480,720,960 min時,三條曲線呈現正相關.

從圖6(b)可得,在下跌趨勢時,k=1,50,100 min的波動率自相關系數均為正值.在周期性特性中,當k=1 min時,在滯后期t=120 min,相關性系數趨于0.15,并以T=240 min的周期微下落式出現;在滯后期t=240 min,相關性系數趨于0.5,并以T=240 min的周期微下落式出現.即波動率曲線以T=120 min的周期呈現出低相關性和高相關性的交替變換,且這一周期性規律在k=100 min時依然存在.在不同k值的相關性特性中,當滯后期t=240,480,720,960 min時,k=1,50,100 min的波動率相關性系數呈正相關,均出現一個大波峰.在滯后期t=120,360,600,840 min時,k=1與k=50 min的相關性函數呈正相關,均為一個小波峰,而對應k=100 min的波動率自相關曲線則呈現出一個小波谷.

上漲、平緩、下跌趨勢的波動率自相關性均高于收益率的自相關性,這與經濟學家的主流趨向一致,即股票價格收益率無長期記憶性,而波動率存在較強的記憶性.而從上述三種趨勢的自相關周期性分析圖,我們發現上證指數在k=1 min與k=100 min時波動率自相關曲線存在明顯的周期性,即我國股市每日開盤價存在較高的相關性,其主要原因可能是由于存在日內模式,這與Zhou等[24]的研究結論一致.但本文嘗試改變樣本的起始值,分別以時間9:27,10:34,11:39,13:51,14:47,15:26的收盤價作為樣本數據的起點,結果發現這一周期性規律仍然不變.這說明了上證指數一分鐘的股價波動深受前期同一時刻股價波動的影響,而不僅僅是日內模式的作用.因此,投資者的研究視角不應僅局限于股市收盤價、開盤價,還應挖掘高頻數據的內在屬性,利用自相關性的周期性規律進行投資決策.同時,研究也發現:下降趨勢的收益率、波動率自相關曲線高于平緩和上漲趨勢的曲線,這也進一步驗證我國股市信息沖擊的非對稱特性,即對利壞信息沖擊的反應大于利好信息的特征一直持續存在.

4.3 多分形

2008年,Calvet和Fisher[25]對多重分形的標度不變性的形式進行改進,多重分形可由時間間隔k的收益比率來表示, 比率若為常數則表示單分形,反之則為多分形.在下面的統計分析中,每組的樣本數據為500個,時間間隔k的取值為5 min,q值分別取1.5,2.0,2.5,3.0,并且在q=3.0時,曲線的變化幅度最為明顯,上漲、平緩和下跌三種趨勢下的收益比率曲線的線性回歸斜率分別為?0.3429,?0.1564以及?0.1515,即三者從小到大依次為上漲趨勢線性斜率、平緩趨勢線性斜率、下跌趨勢線性斜率.具體如圖7所示.

對不同幅度的波動性進行冪次方,相當于對波動的幅度進行放大和縮小,即大波動更大,小波動更小.不同q值對應的尺度函數刻畫不同時點的分形特征,隨著時間標度的變化,可以觀察到不同時間標度下的價格波動信息.從圖7可以看出,不論收益率數據趨于上漲、平緩還是下跌,圖形均為非線性,即股票市場具有多重分形結構.其中,在不同時點上收益的波動幅度雖然各異,但不同市場狀態均呈現出趨勢相似的衰減式長尾圖形,即股價的波動具有持久性或長期依賴關系.由上述分析可知,上證指數在不同的波動趨勢下都具有較強的長記憶性特征.此外,從圖中可以看出,當q越大時,價格增量較大的那些部分的標度行為變化越明顯,這說明價格在不同的變化范圍內,有不同的標度關系,即股市中存在多標度行為.而一般地,對正時間標度方向來說,行情較好時市場的交易量也相對較高,高交易量意味著市場具有高流動性,而高流動性能引發市場的大的價格波動.因此,上漲趨勢較平緩和下跌趨勢最先到達谷底.

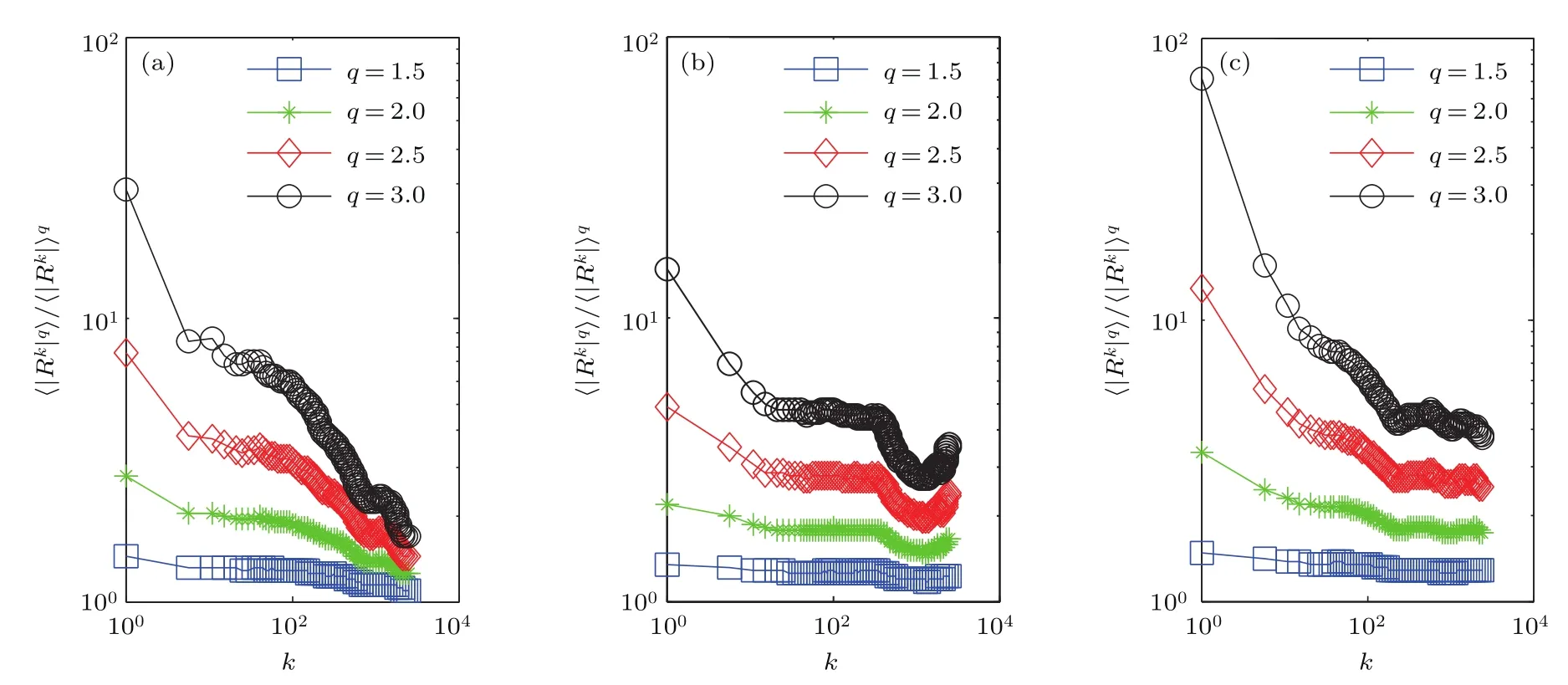
圖7 k=5 min時不同趨勢下的收益比率曲線 (a)上漲趨勢;(b)平緩趨勢;(c)下跌趨勢Fig.7.Curves of ratioversus number k=5 min in di ff erent trends:(a)Rising trend;(b)steady trend;(c)falling trend.

上文是基于不同的q值,以時間增量矩的尺度特性刻畫股市的多重分形結構.下文將選取q=3的曲線測度股市的多重分形特征,并分別分析處于上漲、平緩、下跌市場狀態下收益率的長期、短期波動趨勢.其中,樣本時間序列為3790個,k的取值為5 min.圖8中,紅色曲線為上漲趨勢的收益比率,藍色曲線為平緩趨勢的收益比率,綠色曲線為下跌趨勢的收益比率.

當q=3時,按不同尺度的時間間隔對同一價格時間序列求取收益序列,并對所得收益序列進行適當的尺度變換,圖中各市場狀態下的股市都具有向下傾斜的結構特點,反映了序列整體的穩定性,但上漲趨勢和下跌趨勢的收益率序列衰減速度更快,在短期內具有更明顯的變化趨勢,說明收益率的變化趨勢在一定程度上影響收益率序列的分布.總體而論,不同時間標度(分鐘,日,周,月,年等)下股市收益序列在統計意義上具有相似性.文中分別對不同長度的時間數據和時間間隔取值進行研究,結果表明k越大,所刻畫的圖形越粗糙,但圖形的收斂速度也越快,即可縮短時間尺度并近似估計圖形的變化趨勢.由分形結構的標度不變性可得,不同的時間長度和時間間隔變化并不會改變股市的分形結構.

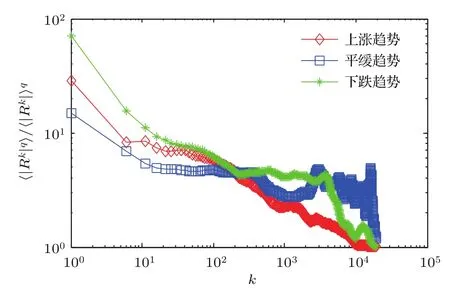
圖 8 k=5 min,q=3 的收益比率 (〈|Rk|q〉/〈|Rk|〉q)曲線Fig.8.Curves of ratio 〈|Rk|q〉/〈|Rk|〉qversus number k=5 min with q=3.

股市分形結構的存在是由于市場中存在大量的具有不同投資期限的投資者和良好的流動性.由圖8可得,上漲趨勢收益率的變化會引起較大的價格波動.這主要是因為投資者在股市處于上漲趨勢時對未來預期樂觀,產生了“樂隊車效應”,從而出現資產流動性過剩,助推資產價格泡沫的形成,即高流動性易引發市場價格的大波動.反之,在短期內,當股市處于下跌趨勢時,市場出現恐慌情緒,由于股權質押、定增或購并中杠桿的廣泛使用,為求自保,有影響力的股東和投資者以各種借口對股票實行停牌處理,這顯著擠壓了場內的流動性;受強制平倉和主動降杠桿的要求,仍然在交易的股票大量跌停,場內流動性基本枯竭;面對潛在的贖回壓力和現金要求,投資者被迫拋售在境外市場、商品市場和債券市場的頭寸,流動性枯竭迅速沖擊到其他領域和地區;同時,流動性枯竭加劇了市場的恐慌情緒,導致整個市場的流動性進一步下降.投資者對未來預期悲觀,容易引發金融資產的大量恐慌拋售,致使市場流動性嚴重不足,最終出現金融市場的資產流動性好像瞬間被掏空的現象,即“流動性黑洞”.因此,此時投資者在股市上謹慎尋求投資機會,但由于市場流動性較低,不活躍的市場往往會導致小的價格波動,即波動趨勢衰減速度較為平緩.

而當股市長期處于低位價格時,對于長期投資者來說,可以低價進入股市,尋求時機以在未來更長的時間內獲得更高收益,因此,當市場從流動性不足恢復至原先的流動性水平,價格波動幅度比上漲趨勢的波動更加顯著.同時,受賣空限制的影響,繁榮情緒更容易在投資者之間傳遞并反映到股價上,即出現“集中式極化”.而賣空限制會導致投資者的悲觀預期無法及時反映到市場上,即減慢資產價格對悲觀信息的調整速度,致使恐慌信息逐漸擴散且傳遞速度較慢,即出現“分散式極化”.對于平緩趨勢的收益率序列,股市的長期記憶性特征最弱,且隨著時間尺度的變化,價格變化出現無規律的振蕩式波動.這一現象也與現有的研究相符,當股市處于平緩時,股票價格的趨勢最不易捕捉.

5 結 論

本文分析了上證指數不同市場狀態下的對數增量在不同時間間隔下的概率分布密度、自相關性和多分形特性.首先,同成熟股市一樣,當時間間隔由1 min變為100 min時,標準化收益率序列的分布向高斯趨近,且在市場為下跌狀態時,尾部更擬合高斯分布.在時間間隔k=1—1000 min的范圍內,三種趨勢對數增量序列的分布均能較好地用列維分布描述,上漲、平緩、下跌趨勢的分布指數、擬合優度不同,而其中在股市下跌時列維分布的擬合效果最好,對于投資決策更具預測價值.其次,在自相關性分析中,上證指數的收益率無長期記憶性,而波動率則存在較強的記憶性,同時,其波動率的自相關性存在明顯的周期性,且在下降趨勢時相關性最高.這是上證指數所特有的周期性,這一效應表明投資者對于市場變化的過度反應導致投資的慣性反沖.而上證指數的自相關性函數較之成熟股市衰減更慢,則表明投資者的投資熱情更多地受到歷史信息的影響.因此,投資者的研究視角不應只限于歷史信息,而應觸及實時的高頻數據,并挖掘其內在屬性,利用自相關性的周期性等規律進行投資決策.最后,上證指數在不同的波動趨勢下都具有很強的長記憶性特征,其主要是由于長期、短期投資決策所引致的流動性水平的變化.上證指數的總體宏觀行為與國際成熟股市較為一致,但在微觀特性存在的差異說明我國股市受宏觀政策、投資者情緒和流動性水平等因素的影響仍較強烈.而股市價格的變化除了受外生性因素的影響外,近年的研究也表明由于內源性反饋流程[26,27],股市內生性的影響水平已顯著增加,即我國股市價格的變化更多地受來自市場訂單、股市結構等微觀因素的影響.

[1]Mantegna R N,Stanley H E 1995 Nature 376 46

[2]Chat fi eld C 2016 The Analysis of Time Series:An Introduction(Boca Raton:CRC Press)pp92–135

[3]Chakraborti A,Toke I M,Patriarca M,Abergel F 2011 Quant.Financ.11 991

[4]Huang J P 2013 Economy Physics(Beijing:Higher Education Press)pp1–7(in Chinese)[黃吉平 2013 經濟物理學(北京:高等教育出版社)第1—7頁]

[5]Zhou R W,Li J C,Dong Z W,Li Y X,Qian Z W 2017 Acta Phys.Sin.66 040501(in Chinese)[周若微,李江城,董志偉,李云仙,錢振偉2017物理學報66 040501]

[6]Parisi D R,Sornette D,Helbing D 2013 Phys.Rev.E 87 012804

[7]Wei Y,Wang P 2008 Physica A 387 1585

[8]Wu P Z,Ma H R 2008 J.Shanghai Jiaotong Univ.42 147(in Chinese)[吳斌哲,馬紅孺2008上海交通大學學報42 147]

[9]Gao Y C,Zeng Y,Cai S M 2015 J.Stats.Mech.2015 03017

[10]Qiu T,Zheng B,Ren F,Trimper S 2007 Physica A 378 387

[11]Gao Y C,Cai S M,Wang B H 2012 J.Stats.Mech.2012 12016

[12]Mandelbrot B B 1963 J.Polit.Econ.71 421

[13]Sornette D,Knopo ffL,Kagan Y,Vanneste C 1996 J.Geophys.Res.101 13883

[14]Zhou W X 2007 Introduction of Econophysics(Shanghai:Shanghai University of Finance and Economics Press)pp17–33(in Chinese)[周煒星 2007金融物理學導論(上海:上海財經大學出版社)第17—33頁]

[15]Mantegna R N,Stanley H E 1994 Phys.Rev.Lett.73 2946

[16]Wang B H,Hui P M 2001 Eur.Phys.J.B 20 573

[17]Issler M,H?ller J,Imamo?lu A 2016 Phys.Rev.B 93 081414

[18]Ncheuguim E K,Appiah-Kubi S,Ofori-Dankwa J 2014 Res.Meth.Strateg.Manag.10 215

[19]Liu S D,Fu Z T,Liu S K 2014 Chin.J.Geophys.57 2751(in Chinese)[劉式達,付遵濤,劉式適2014地球物理學報57 2751]

[20]Ma F,Wei Y,Huang D,Chen Y 2014 Physica A 405 171

[21]Mandelbrot B 1974 J.Appl.Probab.11 437

[22]Zhang T W,Lu W B,Li S 2013 Economist 9 97(in Chinese)[張騰文,魯萬波,李隋 2013經濟學家 9 97]

[23]Wu M C,Huang M C,Yu H C,Chiang T C 2006 Phys.Rev.E 73 019908

[24]Zhou W C,Xu H C,Cai Z Y,Wei J R,Zhu X Y,Wang W,Zhao L,Huang J P 2009 Physica A 388 891

[25]Calvet L E,Fisher A 2008 Multifractal Volatility:Theory,Forecasting,and Pricing(Massachusetts:Acedemic Press)pp23–31

[26]Toth B,Eisler Z,Lillo F,Bouchaud J P,Kockelkoren J,Farmer J D 2012 Quant.Financ.12 1015

[27]Flimonov V,Sornette D 2012 Phys.Rev.E 85 056108

PACS:02.50.–r,02.50.Cw,02.50.Ng,02.60.EdDOI:10.7498/aps.66.120203

Microscopic characteristics of Chinese capital market based on the high frequency data of Shanghai composite index?

Tang Zhen-Peng1)2)3)Chen Wei-Hong1)?Ran Meng1)

1)(School of Economics and Management,Fuzhou University,Fuzhou 350116,China)
2)(Fujian Province Key Laboratory for Financial Innovation of Science and Technology,Fuzhou 350116,China)
3)(Fujian Province Center for Enterprise Development and Research,Fuzhou 350116,China)

6 January 2017;revised manuscript

6 April 2017)

This paper mainly uncovers the typical microscopic characteristics of Chinese capital market in three di ff erent stock price stages of rising,steady and falling based on the high frequency data of Shanghai composite index.Firstly,by analyzing the probability distribution of the Shanghai composite index in di ff erent time intervals,we clearly fi nd that the logarithmic change of the index presents an obvious heavy tail feature as well as non-Gaussian Levy distribution,and the return series converges to a normal distribution with the increase of the time interval,which becomes more signi fi cant especially in the falling stage of stock prices.Secondly,by calculating the autocorrelation function,we observe that unlike the return rate,the fl uctuation ratio of Shanghai composite index demonstrates remarkable long memory volatility with a periodicity of about 240 min,and the autocorrelation curve in falling stage is much higher than in rising and steady stages.Thirdly,in the multi-fractal structure,the volatility of return series has signi fi cant short-term and long-term di ff erences among three di ff erent stages of rising,steady and falling due to the e ff ects of time limitation and liquidity of investment.Finally,the macroscopic behavior of the Shanghai composite index is relatively consistent with that of the international mature stock market,however,the corresponding microscopic characteristics demonstrate signi fi cant di ff erences due to the fact that the Chinese capital market is strongly dependent on the macroeconomic policy,investor sentiment,and liquidity levels.It is quite remarkable that the tail distribution of mature stock market is much fatter than that of Chinese stock market because of the special control and limit mechanism of stock prices in China,which fi nally causes the considerably lower amplitude of price fl uctuation.Moreover,it is also found that the attenuation speed of the autocorrelation function in the Chinese capital market is obviously slower than that in the mature stock market,which suggests that the behaviors of investors in Chinese stock market are more likely to be in fl uenced by the historic exchange information.At the same time,the periodicity of autocorrelation function is actually caused by the inertia recoil of investors,which further veri fi es the information asymmetry of Chinese stock market.Especially,by changing the starting values of the samples,we fi nd that the periodicity of autocorrelation function still remains the same,which indicates that the periodicity characteristic of stock price is not dominated only by the intraday pattern of trading activity.Therefore,the investors should discover the underlying rules of high-frequency data and extract more useful knowledge in order to guide their investment decisions more e ff ectively.

capital market,microscopic characteristics,Shanghai composite index,high frequency data

10.7498/aps.66.120203

?國家自然科學基金(批準號:71573042,71171056)和福建省社科基金青年博士項目(批準號:FJ2016C200)資助的課題.

?通信作者.E-mail:tingling69@163.com

?2017中國物理學會Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.71573042,71171056)and the Society Science Foundation for Young Ph.D.of Fujian Province,China(Grant No.FJ2016C200).

?Corresponding author.E-mail:tingling69@163.com