一種改進(jìn)的支持向量機(jī)參數(shù)尋優(yōu)方法?

呂金銳

（太原城市職業(yè)技術(shù)學(xué)院太原030027）

一種改進(jìn)的支持向量機(jī)參數(shù)尋優(yōu)方法?

呂金銳

（太原城市職業(yè)技術(shù)學(xué)院太原030027）

誤差懲罰參數(shù)和核參數(shù)是決定SVM泛化能力的主要因素，對(duì)這兩種參數(shù)的優(yōu)化是SVM應(yīng)用中需要解決的關(guān)鍵問題之一。論文在研究支持向量機(jī)理論的基礎(chǔ)上，利用一些標(biāo)準(zhǔn)的測(cè)試數(shù)據(jù)集研究了均勻設(shè)計(jì)方法在RBF核參數(shù)優(yōu)化問題上的表現(xiàn)。通過對(duì)比尋優(yōu)精度，發(fā)現(xiàn)和傳統(tǒng)均方設(shè)計(jì)方法相比，采用論文的方法能進(jìn)一步提高精度。

SVM；均方設(shè)計(jì)；RBF核參數(shù)

Class NumberTP18

1 引言

支持向量機(jī)（SVM）是Vapnik等在COLT-92提出的一種新型的機(jī)器學(xué)習(xí)方法，其主要理論基礎(chǔ)為統(tǒng)計(jì)學(xué)習(xí)，并依據(jù)風(fēng)險(xiǎn)最小化原理推導(dǎo)而出。SVM在有限的樣本空間中進(jìn)行統(tǒng)計(jì)分析，在模型的復(fù)雜性和機(jī)器的學(xué)習(xí)能力之間尋找最優(yōu)路徑，從而得到最好的推廣能力［1～2］。與傳統(tǒng)的人工神經(jīng)網(wǎng)絡(luò)、決策樹分類及Kmeans聚類等算法相比，不僅數(shù)據(jù)模型結(jié)構(gòu)簡(jiǎn)單，而且泛化推廣能力更高。

Vapnik及其合作者在統(tǒng)計(jì)研究中發(fā)現(xiàn)，SVM的核函數(shù)主要有四種，不同的核函數(shù)可以構(gòu)造不同的SVM，但對(duì)SVM的分類結(jié)果影響極其有限，然而核函數(shù)參數(shù)的選擇卻是影響SVM性能的關(guān)鍵，也是影響其實(shí)用化的主要障礙之一。如何獲得最優(yōu)的參數(shù)，必須借助相關(guān)的參數(shù)優(yōu)化算法。本文在傳統(tǒng)的均方設(shè)計(jì)方法的基礎(chǔ)上設(shè)計(jì)了一種改進(jìn)的算法，通過實(shí)驗(yàn)分析表明，采用改進(jìn)后的參數(shù)優(yōu)化方法在尋優(yōu)精度上有了提高。

2 支持向量機(jī)基本原理

支持向量機(jī)最初的設(shè)計(jì)是為解決線性（Linear）可分情況的。對(duì)兩類線性可分情況而言，需要找到一條最佳分類線，該分類線不僅要將兩類樣本數(shù)據(jù)無(wú)錯(cuò)誤的分割開，而且必須滿足兩類樣本的分類間隔最大。

假設(shè)線性可分樣本集為{(xi，yi)，i=1，2，3，…，n}，xi∈Rd，yi∈{+1，-1}，其中d代表d維空間，其線性（Linear）判別函數(shù)的表達(dá)式為g(x)=w·x+b，其分類面方程就是w·x+b=0。將判別函數(shù)進(jìn)行歸一化處理，使兩類樣本都滿足||g(x)≥1的條件，由于任意點(diǎn)xi到H的距離為：這樣分類間隔。從表達(dá)式可以推導(dǎo)出，‖‖w最小，分類間隔最大。要求分類面將兩類樣本全部正確的分割，必須滿足：yi(w·xi+b)-1≥0，i=1，2，3，…，n。

計(jì)算支持向量機(jī)的過程就是求最佳分類面的過程。因此可以通過求解下面的二次優(yōu)化問題獲得：

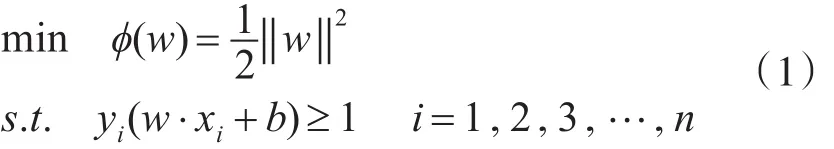
滿足yi(w·xi+b)=1的訓(xùn)練樣本叫做支持向量。式（1）為在約束條件下求極值的過程，可以通過Lagrange優(yōu)化方法將其轉(zhuǎn)化為對(duì)偶問題。具體過程是先求出原問題的Lagrange函數(shù)：，其中αi≥0為L(zhǎng)agrange乘子，再對(duì)式中的w和b求偏導(dǎo)并令其等于0。將得到的等式代回原Lagrange函數(shù)，從而得到對(duì)偶目標(biāo)函數(shù)。

若α*i為最優(yōu)解，則該分類面的權(quán)向量和偏移量分別為和b*=yi-w*·xi，這是一個(gè)二次規(guī)劃問題，存在唯一的解，即全局最優(yōu)解。從表達(dá)式中可以推導(dǎo)出，α*i=0的樣本對(duì)w*不起作用，只有不等于0的樣本對(duì)w*起作用，從而影響分類結(jié)果。α*i≠0的樣本被定義為SV，因?yàn)樗鼈冎瘟苏麄€(gè)最優(yōu)分類面，所以叫支持向量。最終的決策函數(shù)為

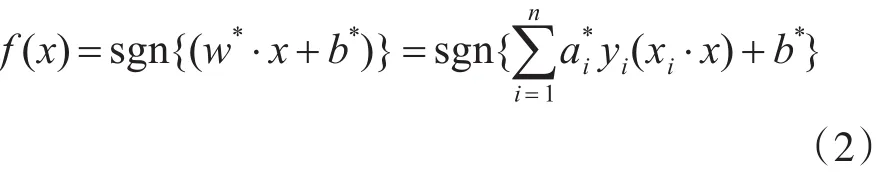
首先提取待分類樣本的特征向量，將特征向量輸入決策函數(shù)，輸出即為該樣本的分類結(jié)果。

考慮線性不可分的情況，可引入核函數(shù)的概念。其基本原理是在當(dāng)前維度無(wú)法分割的樣本點(diǎn)映射到高緯度空間進(jìn)行分割。在特征空間中構(gòu)造最優(yōu)分類超平面時(shí)，假設(shè)非線性映射為?，其訓(xùn)練算法僅使用空間中的點(diǎn)積?(xi)·?(xj)。根據(jù)泛函的相關(guān)理論，只要某一函數(shù)K(xi，xj)滿足Mercer條件，即該函數(shù)為半正定函數(shù)，那么它就可以作為核函數(shù)，并且對(duì)應(yīng)某一變換空間中的內(nèi)積。因此選擇合適的核函數(shù)可實(shí)現(xiàn)空間變換后的線性分類，但模型的復(fù)雜度不變，此時(shí)的目標(biāo)函數(shù)函數(shù)變換為

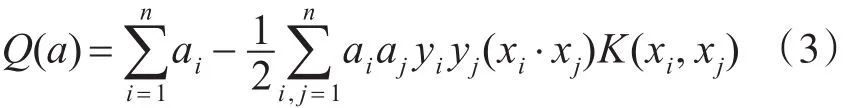
相應(yīng)的決策函數(shù)為

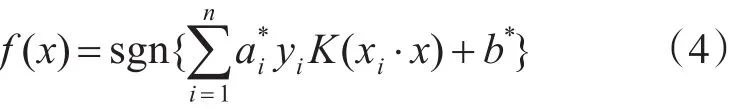
采用不同的內(nèi)積函數(shù)將推導(dǎo)出不同的SVM表達(dá)形式，其內(nèi)積函數(shù)也稱之為核函數(shù)，常用的核函數(shù)有線性核函數(shù)（linear）、多項(xiàng)式核函數(shù)（polynomi?al）、徑向基核函數(shù)（RBF）以及二層神經(jīng)網(wǎng)絡(luò)核函數(shù)（Sigmoid tanh）等。

核函數(shù)K(xi，xj)、映射函數(shù)?(x)以及高維特征空間F是一一對(duì)應(yīng)的，核函數(shù)直接影響支持向量機(jī)樣本點(diǎn)投影到高維空間的分布。支持向量機(jī)為了構(gòu)造最優(yōu)分類超平面，獲得較高的推廣性能，需要樣本數(shù)據(jù)點(diǎn)在高維特征空間有良好的分布。很多實(shí)驗(yàn)結(jié)果表明，在沒有任何先驗(yàn)知識(shí)的數(shù)據(jù)情況下，選擇RBF核進(jìn)行支持向量機(jī)學(xué)習(xí)往往可以取得很好的分類效果；同時(shí)，目前針對(duì)RBF核SVM的研究比較多，各種實(shí)驗(yàn)結(jié)果也較多，便于和本文的結(jié)果進(jìn)行比較［4］。

3 支持向量機(jī)參數(shù)優(yōu)化問題

在機(jī)器學(xué)習(xí)中，學(xué)習(xí)現(xiàn)有的規(guī)律進(jìn)行總結(jié)并對(duì)未知的知識(shí)進(jìn)行判斷決策，這樣的能力稱之為推廣性能。在SVM中，核參數(shù)λ和誤差懲罰參數(shù)C是影響其推廣性能的主要影響因素。核參數(shù)λ的改變可以影響映射函數(shù)，從而改變樣本在高維特征空間的分布，而對(duì)于支持向量機(jī)問題來(lái)說(shuō)，在高維特征空間構(gòu)造最優(yōu)分類超平面直接影響其推廣性能，所以核參數(shù)λ對(duì)支持向量機(jī)的推廣性能影響巨大。誤差懲罰參數(shù)C的作用是確定針對(duì)出現(xiàn)誤差的容忍度［5～6］，C越大，越不能容忍出現(xiàn)的誤差。

因此可以得出結(jié)論，選擇合適的參數(shù)，并對(duì)參數(shù)進(jìn)行優(yōu)化，是保證支持向量機(jī)進(jìn)行機(jī)器學(xué)習(xí)并獲得優(yōu)良推廣能力的前提條件。

常用的優(yōu)化算法有網(wǎng)格搜索、均方設(shè)計(jì)方法、遺傳算法、核校準(zhǔn)算法和雙線性搜索方法等。本文主要是通過研究均方設(shè)計(jì)方法，在此基礎(chǔ)上做了進(jìn)一步改進(jìn)。

均勻設(shè)計(jì)方法是在20世紀(jì)80年代由方開泰，王元等提出的指導(dǎo)試驗(yàn)設(shè)計(jì)的方法。其目的是在多個(gè)影響因素，每個(gè)因素又有多個(gè)水平的情況下，通過在試驗(yàn)范圍內(nèi)挑選具有代表性的試驗(yàn)點(diǎn)，以盡量少的試驗(yàn)次數(shù)，達(dá)到最優(yōu)效果。均勻設(shè)計(jì)思想的本質(zhì)是在一個(gè)參數(shù)空間，挑選一些點(diǎn)，使其均勻分布在參數(shù)空間，這些均勻設(shè)計(jì)點(diǎn)可以代表整個(gè)參數(shù)空間的分布

要獲得均勻設(shè)計(jì)點(diǎn)，需要運(yùn)用均勻設(shè)計(jì)表。均勻設(shè)計(jì)表取決于參數(shù)的因素?cái)?shù)和水平數(shù)；在參數(shù)優(yōu)化過程中，影響結(jié)果的參數(shù)即為因素；水平指每個(gè)因素在試驗(yàn)允許范圍內(nèi)選取的具有代表性的幾個(gè)取值。本文所要優(yōu)化的參數(shù)是誤差懲罰參數(shù)和核參數(shù)，即因素?cái)?shù)為2；參數(shù)搜索的區(qū)間為[2-15，215]，水平數(shù)為31［7］。

均勻設(shè)計(jì)的實(shí)驗(yàn)方法是：每個(gè)影響因素的每個(gè)水平線上只進(jìn)行一次試驗(yàn)；任何兩個(gè)影響因素的試驗(yàn)點(diǎn)在平面方格的交叉點(diǎn)上，每一行每一列有且僅有一個(gè)試驗(yàn)（交叉）點(diǎn)；其目的是保證實(shí)驗(yàn)樣本在實(shí)驗(yàn)范圍內(nèi)的均勻分布。當(dāng)影響因素的水平數(shù)增加時(shí)，試驗(yàn)次數(shù)按照水平數(shù)的增加量而增加。

在支持向量機(jī)參數(shù)優(yōu)化中執(zhí)行均勻設(shè)計(jì)的算法步驟主要是：

1）根據(jù)參數(shù)和參數(shù)搜索區(qū)域，確定均方設(shè)計(jì)因素為2，水平數(shù)為31；

2）利用均方設(shè)計(jì)軟件，根據(jù)因素?cái)?shù)和水平數(shù)生成均方設(shè)計(jì)表格；

3）根據(jù)均方設(shè)計(jì)表格，在參數(shù)空間選取31個(gè)均方設(shè)計(jì)點(diǎn)；

4）在均方設(shè)計(jì)點(diǎn)上涌支持向量機(jī)回歸（SVR）擬合曲面，以代表整個(gè)參數(shù)空間上的正確率情況；

5）計(jì)算生成曲面上每個(gè)參數(shù)點(diǎn)的5重交叉檢驗(yàn)正確率，從而找出最佳的參數(shù)組。

在本文支持向量機(jī)參數(shù)優(yōu)化實(shí)驗(yàn)中，利用均勻設(shè)計(jì)方法，選出31個(gè)均勻設(shè)計(jì)點(diǎn)，計(jì)算5重交叉檢驗(yàn)正確率，計(jì)算量為31×5，相比較網(wǎng)格搜索，均勻設(shè)計(jì)計(jì)算量大大減少，效率有很大的提高。

由于均勻設(shè)計(jì)方法是在均勻設(shè)計(jì)點(diǎn)上擬合曲面來(lái)代表整個(gè)參數(shù)區(qū)域上面的正確率分布情況，所以當(dāng)均勻設(shè)計(jì)點(diǎn)取得過少時(shí)，有可能曲面的擬合精度不夠，所以針對(duì)這一問題，提出了一種改進(jìn)的方法，如圖1所示。

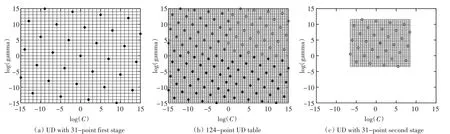
圖1SVM參數(shù)優(yōu)化均勻設(shè)計(jì)改進(jìn)方法

首先將原來(lái)的參數(shù)區(qū)間劃分為四個(gè)相同小區(qū)間，在每個(gè)區(qū)間上分別取31個(gè)均勻設(shè)計(jì)點(diǎn)。分別用四個(gè)區(qū)間中的點(diǎn)進(jìn)行支持向量機(jī)（SVM）擬合曲面，在曲面上找出正確率最大的點(diǎn)，即得到局部最優(yōu)點(diǎn)。

然后在這些局部最優(yōu)點(diǎn)周圍建立一個(gè)小的搜索區(qū)間，對(duì)這四個(gè)小區(qū)間進(jìn)行更精確地搜索，從而找出最優(yōu)參數(shù)，即“嵌套式”均勻設(shè)計(jì)方法［8］。

本文通過調(diào)用標(biāo)準(zhǔn)數(shù)據(jù)集對(duì)該方法進(jìn)行了驗(yàn)證。標(biāo)準(zhǔn)數(shù)據(jù)集主要包括訓(xùn)練數(shù)據(jù)和測(cè)試數(shù)據(jù)兩部分。訓(xùn)練數(shù)據(jù)主要用于訓(xùn)練生成支持向量機(jī)的模型；測(cè)試數(shù)據(jù)用來(lái)預(yù)測(cè)支持向量機(jī)的推廣性能。每一個(gè)數(shù)據(jù)點(diǎn)包括兩部分，樣本和標(biāo)簽，對(duì)于兩類分類問題，數(shù)據(jù)點(diǎn)的標(biāo)簽均為［-1，+1］。

本文中，采用以下標(biāo)準(zhǔn)數(shù)據(jù)集［9］，這些數(shù)據(jù)集的輸入維數(shù)從2～60，訓(xùn)練數(shù)據(jù)個(gè)數(shù)從140～1000，測(cè)試數(shù)據(jù)個(gè)數(shù)從75～7000均不等，且跨越范圍很大，使得本文更有說(shuō)服力。

4 實(shí)驗(yàn)結(jié)果分析

在實(shí)現(xiàn)優(yōu)化算法的過程中，本文利用Matlab編程。本文試驗(yàn)都是在配置為2.0GHz雙核處理器，1GB內(nèi)存的計(jì)算機(jī)上進(jìn)行。為了對(duì)比算法的精度，編程輸出支持向量機(jī)最優(yōu)參數(shù)的5重交叉檢驗(yàn)正確率。

由圖2可以發(fā)現(xiàn)，傳統(tǒng)均勻設(shè)計(jì)方法與改進(jìn)后的優(yōu)化方法所獲得的正確率差別不大，但是在小范圍內(nèi)提高了正確率。由圖3可以看出均勻設(shè)計(jì)方法和改進(jìn)方法在參數(shù)空間擬合的曲面正確率變化趨勢(shì)［10］，在最優(yōu)參數(shù)點(diǎn)附近都是基本相同的，而且均勻設(shè)計(jì)點(diǎn)有良好的空間覆蓋性，并且可以很好地代表空間的特性，可見改進(jìn)后的方法是可行的。

圖2支持向量機(jī)最優(yōu)參數(shù)的5重交叉檢驗(yàn)正確率

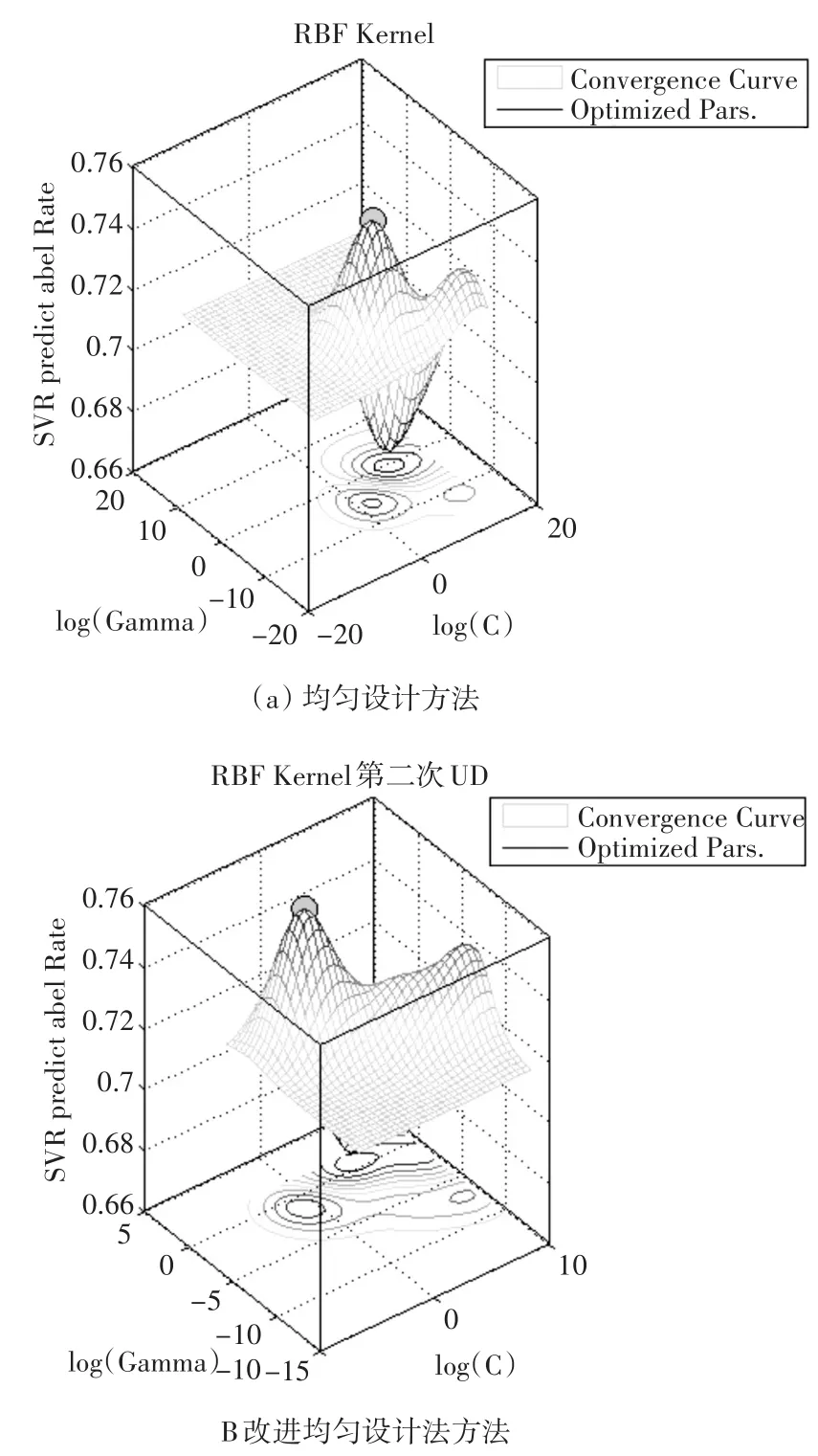
圖3數(shù)據(jù)集breast-cancer均勻設(shè)計(jì)方法比較

利用本文的方法對(duì)懲罰因子進(jìn)行最優(yōu)查找，采用本文的方法獲得最優(yōu)懲罰因子為0.5，而傳統(tǒng)的均方設(shè)計(jì)方法獲得的最優(yōu)懲罰因子為1。將獲得的懲罰因子進(jìn)行支持向量機(jī)的圖像分割，由實(shí)驗(yàn)結(jié)果可以發(fā)現(xiàn)，采用本文的方法能進(jìn)一步提高分割精度，如圖4所示。

圖4懲罰因子尋優(yōu)結(jié)果比較

通過分類示意圖，發(fā)現(xiàn)采用改進(jìn)后的均方設(shè)計(jì)方法能小幅減少支持向量的個(gè)數(shù)，從而提高分類的精度，如圖5所示。

圖5分類示意圖

從圖5中可以發(fā)現(xiàn)，（a）為傳統(tǒng)均方設(shè)計(jì)方法，其支持向量的個(gè)數(shù)為24個(gè)，分類錯(cuò)誤率為13.04%，采用改進(jìn)的方法其支持向量的個(gè)數(shù)為21個(gè)，分類錯(cuò)誤率為6.52%。

5 結(jié)語(yǔ)

懲罰因子C越大，對(duì)錯(cuò)分樣本的懲罰度越大，錯(cuò)分樣本數(shù)將減少，分類間隔將逐漸減小，分類器的維數(shù)越來(lái)越高，分類器的泛化性能將變差；反之，隨著懲罰因子C值的減小，對(duì)錯(cuò)分樣本的懲罰度減小，錯(cuò)分樣本數(shù)將增多，分類間隔逐漸增大，分類器的維數(shù)將逐漸減小，分類器的泛化性能也逐漸變差，因此需要在參數(shù)空間中進(jìn)行最優(yōu)查詢，而采用本文的參數(shù)尋優(yōu)方法是可行的。

［1］鄧乃陽(yáng).數(shù)據(jù)挖掘中的新方法-支持向量機(jī)［M］.北京：科學(xué)出版社，2003：63-64. DENG Naiyang.New method in data mining-support vec?tor machine［M］.Beijing：Science Press，2003：63-64.

［2］Vapnik V.N.The Nature of Statistical Learning Theory［M］.New York：Springer，2000：171-176.

［3］丁世飛，齊丙娟，譚紅艷.支持向量機(jī)理論與算法研究綜述［J］.電子科技大學(xué)學(xué)報(bào)，2011（1）：3-4. DING Shifei，QI Bingjuan，TAN Hongyan.An Overview on Theory and Algorithm of Support Vector Machines［J］. Journal of University of Electronic Science and Technolo?gy of China，2011（1）：3-4.

［4］李俊飛.一種支持向量機(jī)在線學(xué)習(xí)分類算法［J］.伊犁師范學(xué)院學(xué)報(bào)（自然科學(xué)版），2015（4）：56-57. LI Junfei.An Online Learning Algorithm for Classifica?tion of Support Vector Machine［J］.Journal of Yili Normal University（Natural Science Edition），2015（4）：56-57.

［5］閆國(guó)華.支持向量機(jī)回歸的參數(shù)選擇方法［J］.計(jì)算機(jī)工程，2009，35（13）：218-220. YAN Guohua，ZHU Yongsheng.Parameters Selection Method for Support Vector Machine Regression［J］.Com?puter Engineering，2009，35（13）：218-220.

［6］Liu Yu-Hsin.Global maximum likelihood estimation pro?cedure multinomial probit（MNP）model parameters［J］. Transportation Research Part B：Methodological，2008，34（5）：419-449.

［7］栗志意，張衛(wèi)強(qiáng)，何亮，等.基于核函數(shù)的IVEC-SVM說(shuō)話人識(shí)別系統(tǒng)研究［J］.自動(dòng)化學(xué)報(bào)，2014（4）：780：782. LI Zhiyi，ZHANG Weiqiang，HE Liang.Speaker Recogni?tion with Kernel Based IVEC-SVM［J］.Acta Automatica Sinica，2014（4）：780：782.

［8］梁亮，楊敏華，李英芳.基于ICA與SVM算法的高光譜遙感影像分類［J］.光譜學(xué)與光譜分析，2010，10（30）：2724-2726. LIANG Liang，YANG Minhua，LI Yingfang.Hyperspectral Remote Sensing Image Classification Based on ICA and SVM［J］.Algorithm.Spectroscopy and Spectral Analysis，2010，10（30）：2724-2726.

［9］Hyvarinen.A.Fast and robust fixed-point algorithms for independent component analysis［J］.IEEE Transactions on Neural Networks，1999，4：895-896.

［10］張倩，楊耀權(quán).基于支持向量機(jī)核函數(shù)的研究［J］.電力科學(xué)與工程，2012，5（28）：42-43. ZHANG Qian，YANG Yaoquan.Research on the Kernel Function of Support Vector Machine［J］.Electric Power Science and Engineering，2012，5（28）：42-43.

An Improvement of Support Vector Machine Parameter Optimization Method

LV Jinrui
（Taiyuan City Vocational College，Taiyuan030027）

The penalty parameter and the kernel parameter are the main factors to determine SVMs'generalization perfor?mance and the optimization of these two parameters is one of the key issues，which needs to be solved in the application of SVM. Based on the research of SVM theory，through programming，the paper uses some standard test data sets to compare the perfor?mance of uniform design method in the RBF kernel SVM parameter optimization problems.Through the comparison of accuracy，it is showed that the further precision can be obtained compared with the traditional method.

SVM，uniform design，RBF kerne

TP18

10.3969/j.issn.1672-9722.2017.07.017

2017年1月3日，

2017年2月27日

呂金銳，男，碩士，研究方向：計(jì)算機(jī)網(wǎng)絡(luò)技術(shù)、數(shù)字圖像處理。