結合質心思想和柯西變異策略的粒子群優化算法

呂立國，季偉東

(哈爾濱師范大學 計算機科學與信息工程學院，哈爾濱 150025)

結合質心思想和柯西變異策略的粒子群優化算法

呂立國，季偉東*

(哈爾濱師范大學 計算機科學與信息工程學院，哈爾濱 150025)

(*通信作者電子郵箱kingjwd@126.com)

針對基本粒子群優化(PSO)算法收斂精度低、容易陷入局部最優的問題，提出了一個結合質心思想和柯西變異策略的粒子群優化算法。首先，在粒子的初始化階段采用混沌初始化策略，以提高初始粒子的均勻分布能力；其次，為了提高粒子群的收斂速度和尋優能力，引入了質心的概念，通過計算獲得種群中所有粒子所構成的全局質心和所有個體極值構成的個體質心，使得粒子群內部可以實現充分的信息共享；為避免粒子陷入局部最優解，在粒子群算法中引入了柯西變異運算對當前最優粒子進行擾動，并依據柯西變異運算的規律，適應性地調整擾動步長,該算法以群體多樣性為依據,動態調整慣性權重；最后，使用7個經典的測試函數對算法進行驗證，通過函數運行結果的均值、方差和最小值能夠表明，新算法在收斂精度上有較好的優越性。

粒子群優化算法；質心；柯西變異；群體多樣性；收斂精度

0 引言

粒子群優化(Particle Swarm Optimization, PSO)算法是由Eberhart和Kennedy于1995年提出的一種通過模擬鳥群覓食行為而發展起來的隨機搜索算法[1-2]。PSO算法沒有過多需要調節的參數，因而簡單易行，目前已廣泛應用于各類約束優化[3-4]、數據挖掘[5]，以及工程應用[6-8]等領域。

在標準粒子群優化算法中，粒子的更新僅僅與種群的最優粒子和自身的歷史最優值有關，這種粒子更新機制導致大量的種群進化信息被浪費，Chen等[9]提出生命周期和領導年齡的概念，當一個粒子已經長時間領導群體的進化方向時，允許其他粒子取代其領導地位。Shi等[10]提出慣性權重的概念，有效調節了上一時刻粒子速度對進化過程的影響程度。慣性權重是一種調節群的全局探索和局部挖掘能力的機制,慣性權重ω通過控制之前的速度來調節粒子的沖力。文獻[11]提出了一種負反饋系統，該系統由多樣性控制器(Diversity Controller)、微粒群優化器(PSO Optimizer)和微粒群體(Swarm)三部分組成，根據種群的多樣性來調整慣性權重。湯可宗等[12]從幾何角度提出中心概念，文獻[13]將擾動策略和變異運算引入PSO，一定程度上增加了群體多樣性，從而減小算法陷入局部最優的可能。劉朝華等[14]提出了一種雙態免疫微粒群算法，將微粒群分為捕食和探索兩種狀態，同時引入免疫克隆選擇和受體編輯機制，增強了群體逃離局部最優的能力。邱飛岳等[15]引入了隨即變量分解策略，將合作協同進化框架融合于多目標粒子群優化算法，最后用加法二進制ε指標、超體積指標(HyperVolume, HV)和算法運行時間對算法性能進行分析，實驗結果表明該算法可以有效解決多目標粒子群算法在大規模變量方面的缺陷，并在求解精度和運行效率上有顯著提升，但是依然存在陷入局部最優的缺陷。

以上的改進策略一定程度上提高了粒子群算法的性能,但是如果單純地用質心去替換種群最優粒子，會大大降低種群多樣性; 改變慣性權重和施加擾動操作的確是會對增加種群多樣性有一定幫助,但同時也會降低種群的收斂速度。

本文通過對柯西變異算法和基于質心的粒子群算法的研究和改進，提出了一種結合質心思想和柯西變異策略的粒子群優化算法(Centroid and Cauchy Mutation Particle Swarm Optimization, CCMPSO)。該算法在初始化階段采用Logistic混沌初始化策略，慣性權重根據種群多樣性進行自適應調整，引入質心的思想，計算個體極值質心和種群質心，將其添加到粒子的速度更新公式中，使用柯西變異策略，對全局最優施加變異操作。仿真實驗結果表明該算法的收斂速度和尋優能力要優于PSO和許多改進PSO。

1 粒子群算法

標準粒子群算法是一種群體智能算法，群體中的每個成員被稱為粒子，在搜索空間中以一定的速度尋找最優值。每個粒子根據個體極值pbest和全局極值gbest來更新自己的位置和速度。設在D維搜索空間中，一個大小為N的種群，其中第i個粒子的速度矢量可以表示為Vi={Vi1,Vi2,…，ViD}，位置矢量可以表示為Xi={Xi1,Xi2,…，XiD}，第i個粒子到目前為止所找到的最優位置計為pbesti={pbesti1,pbesti2,…，pbestiD}，整個種群找到的最優位置計為gbest={gbest1,gbest2,…，gbestD}，粒子xi的位置和速度更新公式如下：

(1)

(2)

其中：i=1,2,…,N，j=1,2,…，D，N為種群規模，D為搜索空間的維數；c1、c2為學習因子；t為當前迭代次數；r1、r2是[0,1]的隨機數；為了避免粒子飛出搜索空間，速度Vij通常被限制在某個搜索區域內[-Vmax,Vmax]。

從式(1)可以看出，粒子群具有自我總結和向全局最優個體學習的能力，粒子的速度更新公式主要受三方面因素的影響：第一部分為上一時刻的速度，作為之前搜索方向的記憶；第二部分為認知分量，它模擬了該粒子最好位置的記憶；第三部分稱為社會分量，它刻畫了個體試圖達到的標準，對粒子的速度更新具有重要影響。即在迭代過程中逐步向自己的歷史最優pbest和種群的全局最優gbest靠近。c1調節粒子飛向pbest的步長，c2調節粒子飛向gbest的步長，共同引導粒子飛向粒子群中的最好位置。

在粒子群優化算法中，由于粒子的速度和方向受到gbest的極大影響，如果當前種群所找到的最優解只是整個搜索空間中的局部極值，那算法將會陷入局部最優，尋優效果大大降低； 并且粒子僅依賴于個體最優和全局最優將導致粒子無法從其他的較優粒子那里獲得搜索信息，大量的種群搜索信息被浪費。

2 相關研究

2.1 Logistic映射粒子群優化算法

文獻[16]在PSO粒子初始化的階段引入了混沌序列來提高初始種群的質量，并對陷入局部最優的粒子實行差分變異操作。混沌狀態類似于隨機運動，混沌具有遍歷性、隨機性和規律性等特點。依靠混沌映射序列對粒子的速度和位置進行初始化，不僅保證了粒子的隨機性，而且使得初始粒子因為混沌的遍歷性而具有多樣性的特點，達到在搜索空間中均勻分布的效果。Logistic 映射粒子群優化(Logistic Map Particle Swarm Optimization, LMPSO)算法根據Logistic映射形式得到混沌序列yn+1, j，然后映射到搜索區間[aj,bj]：

xn, j=aj+(bj-aj)×yn, j

(3)

其中：j=1,2,…，D，xn即為種群的一個可行解，粒子速度的初始化方法和位置的初始化方法一樣，只是將變量的取值范圍改為速度的限定范圍。

2.2 質心粒子群優化算法

汪永生等[17]從物理角度提出質心概念，根據所有粒子的個體最優記錄計算出質心，將其與全局最優記錄進行比較和替換，更新全局最優；同時還提出了質心粒子群優化(Centroid Particle Swarm Optimization, CPSO)算法，通過計算出的質心，引導粒子更快地飛向最優位置，有效提高了算法的收斂速度，但是種群的多樣性會下降較快，算法容易陷入局部最優。

2.3 柯西變異粒子群優化算法

文獻[18]將柯西變異操作加入到粒子群算法當中，康嵐蘭等提出，在基本PSO算法收斂之前，全局極值gbest的搜索空間具有局限性，總是徘徊于幾個候選解之間，如果加大gbest的搜素范圍，將有效降低陷入局部最優和過早收斂的可能。 其柯西變異策略為：

gbest*(i)=gbest(i)+u(i)·F(xm)

(4)

式中：u(i)是各維變異權重的平均值，F(xm)是標準柯西分布函數。

2.4 CCMPSO

本文提出的CCMPSO算法是結合了質心思想、柯西變異和混沌初始化的綜合優化算法，并對慣性權重實施動態調整策略。在算法的初始化階段，使用Logistic混沌映射產生初始種群，按照如下方程進行反復迭代：

x(t+1)=μx(t)(1-x(t))

(5)

其中：t為時間步，又稱迭代次數；x代表一個粒子及搜索空間中的一個可行解；μ為調節參數。首先在(0,1)隨機產生一個D維的基準粒子y0，y0=(y01,y02,…，y0D),將此粒子作為Logistic映射的初始迭代粒子，根據Logistic映射的形式，得到混沌序列xn+1, j，即：

yn+1, j=μyn, j(1-yn, j)；n=0,1,2，…,N,j=1,2,…,D

(6)

然后，將粒子根據式(5)映射到搜索空間[-R,R]中：

xn+1, j=R×(2×yn+1, j-1)

(7)

其中：n=0,1,2,…,N,j=1,2,…,D，這樣就產生了N個D維的粒子，對應搜索空間中的N個可行解，即構成算法的初始種群。同樣，粒子的速度初始化類似于位置初始化，只不過將搜索空間改為粒子的速度限定值[Vmin,Vmax]。

慣性權重方面采用依據種群多樣性動態改變的策略，首先計算群體多樣性：

(8)

其中：N為種群規模，D為粒子維數，pj為種群的質心，L是搜索空間最大對角距離。閾值為：

(9)

其中：T為最大迭代次數；t是當前迭代次數；a和b是調節參數，取值(0,1)。

在算法的運行初期，群體多樣性較高，粒子搜索到的位置一般較差，種群需要較強的全局尋優能力讓粒子去探索更多的位置； 在算法運行的后期，種群多樣性降低，粒子一般聚集在全局最優的附近，因此種群需要更高的局部挖掘能力來找出最優值。本文使用文獻[19]中提出的公式作為調節系數的參考標準：

jd=F(gbest(t))/Favg

(10)

其中：F(gbest(t))是全局最優的適應度函數，Favg是平均適應度函數。從式(10)中可以看出jd的取值范圍是(0,1]。

如果dis≤dis′，說明此時的種群多樣性較低，需要較高的慣性權重增加粒子全局尋優的能力，所以令：

(11)

如果dis>dis′，說明此時的種群多樣性較高，需要較低的慣性權重增加粒子局部挖掘能力，所以令：

(12)

式中：ωmax是慣性權重的最大值，一般取0.9；ωmin是慣性權重的最小值，一般取0.4；ω2為調節部分，動態改變慣性權重。

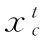
(13)

(14)

將式(13)、(14)和慣性權重ω引入式(1)得到式(15)：

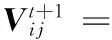
(15)

其中:?是[0,1]的一個常數，稱為權重調節因子；c1、c2、c3是學習因子；r是[0,1]的隨機數。基于式(14)和式(2)對粒子進行速度更新和位置更新，使得粒子在運動過程中不僅依靠個體最優和全局最優，還要依靠其他粒子的個體最優解和全局最優解，增強了群體內部的信息交流能力, 有效提高了PSO算法的收斂性能。

變異算子包括高斯變異(Gaussian mutation)和柯西變異(Cauchy mutation)[20]。相對于高斯變異算子，柯西分布最大的特點是具有較長的兩翼，即產生的隨機數的范圍更大，使得粒子有更大的幾率跳出局部極值[21]，同時較低的峰值使得柯西變異操作將花費更少的時間代價來搜索鄰近區域。本文的算法采用標準的柯西分布對gbest進行變異操作：

(16)

(17)

其中：gbestj是全局最優的第j維分量；η為變異權重，隨著迭代次數的增加而減小；λ是常數，本文中取10；C(0,1)是比例參數t=1的柯西概率分布產生的一個隨機數，該方法使得算法在前期發生較大程度的變異，在后期發生較小程度的變異，使得算法既具有收斂能力，又可以避免陷入局部最優。

2.5 算法的執行過程

算法的流程如圖1所示。圖中評價粒子的操作主要是判斷粒子在更新過速度和位置之后，是否位于更好的位置，如果是，則將其設置為粒子的個體最優；同樣判斷種群中的全局最優是否發生了改變，如果是，則更新全局最優。

圖1 算法流程Fig. 1 Flow of the algorithm

3 仿真實驗及結果分析

本文使用表1中的7個基準測試函數來測試本文提出的CCMPSO算法性能，其中：f1、f2是單峰函數，f3～f7是多峰函數，對每個函數獨立運行20次，對運行后的最優結果求出平均值、標準差和最小值。PSO是基本的PSO算法；CPSO是在PSO的基礎上增加了群體質心，用來引導粒子的速度進行更新；CMPSO是在PSO的基礎上增加了柯西變異的策略，為了增加群體的多樣性，使粒子跳出局部最優；LMPSO是引入了混沌初始化的粒子群優化算法，一定程度上提高了初始種群的質量。為了增強可比性，本次實驗各算法的種群規模都相同N=30，c1=c2=2，維數D=150。實驗的運行環境為Microsoft Windows 7操作系統，Intel CORE i5處理器，4 GB內存，在Matlab R2014b語言環境下編寫測試程序。

為了能夠更真實地比較各種算法的尋優效果，每個測試函數均在上述條件下運行多次，計算統計結果進行比較(均值、標準差和最小值)，結果如表2所示。從表2的實驗結果可以看出:本文所提出的綜合算法在7個測試函數中得到20個最優值; CPSO和CMPSO各取得2個最優結果; 綜合算法CCMPSO在大部分的測試函數上的表現都明顯優于PSO和其他幾種優化算法，且在函數f2和f5上相比PSO體現出較大優勢，特別在f4和f5測試函數上收斂到最小值0。就收斂均值單項而言，CCMPSO均優于本文所列的PSO等其他算法，可見收斂性能較優。就算法運行時間而言，由于CCMPSO算法引入了柯西變異

操作和求取質心的操作，所以運行時間相對有所增加，但時間差距一般保持在5 s左右，特別地對于f6和f7函數，因為以上五種算法均迭代2 400次，所以運行時間較長。

表1 基準測試函數Tab. 1 Benchmark functions

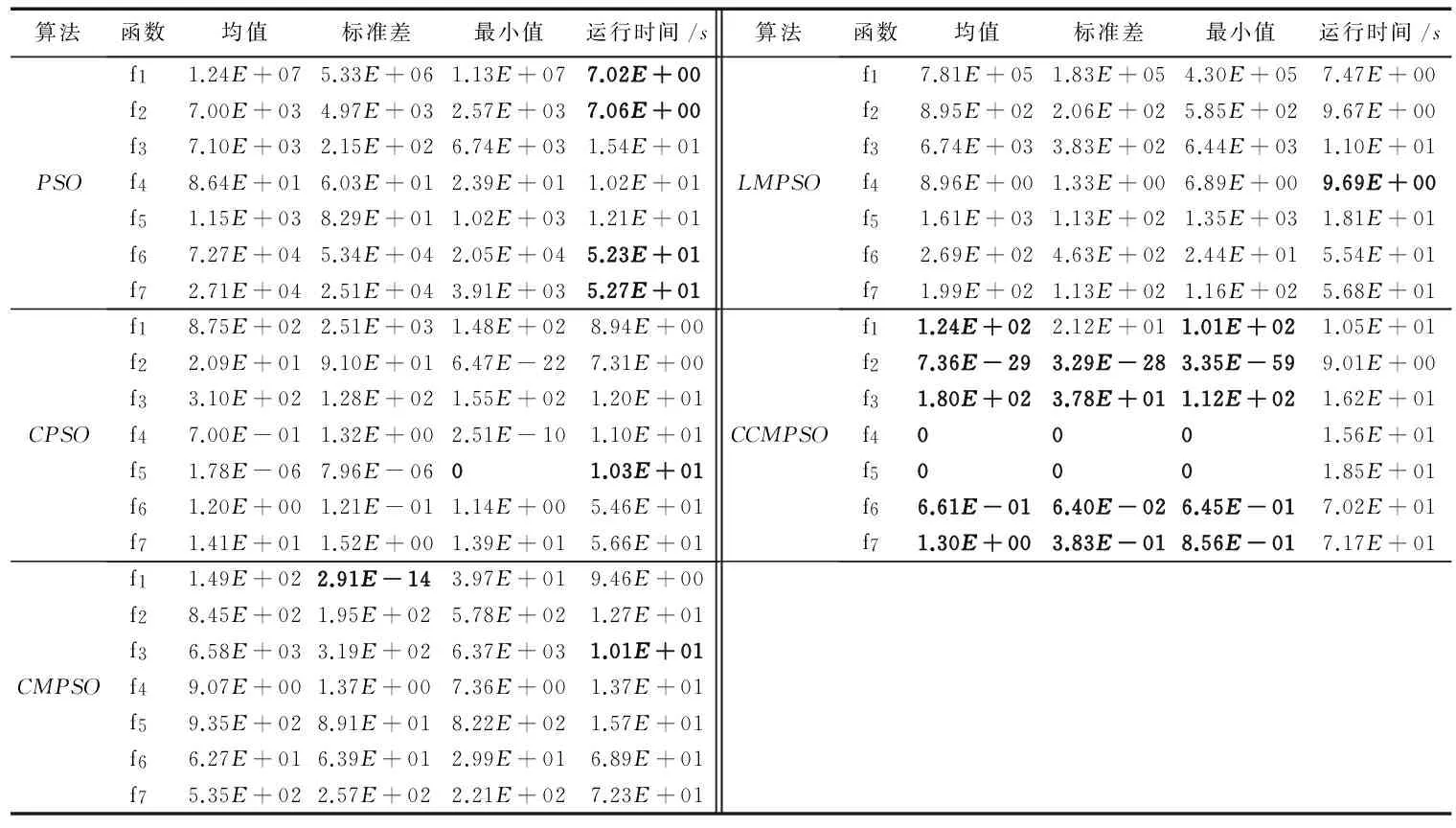
表2 各算法仿真結果 Fig. 2 Simulation results of the algorithms

表3是10維和30維運行結果，維數較低時CCMPSO算法的優越性不是特別明顯，特別是在f6和f7測試函數的尋優過程中，其收斂結果并不理想。算法的穩定性采用李雅普諾夫穩定性理論進行分析，把全局最優位置Pg、個體最優位置Pi、種群質心Xc、個體極值質心Pc假設為隨時間不變的變量，即時不變；而慣性權重ω、認知系數c1、社會系數c2、質心系數c3是線性變化的變量。首先根據式(15)和式(2)得到CCMPSO的進化方程，如下所示:

vi(t+1)=ωvi(t)+c1r1[Pi-xi(t)]+c2r2[Pg-xi(t)]+c3r3[?Xc+(1-?)Pc-xi(t)]

(18)

xi(t+1)=xi(t)+vi(t+1)

(19)

從式(19)可以得到：

vi(t+1)=xi(t+1)-xi(t)

將其代入速度進化方程可得：

xi(t+1)-xi(t)=ω[xi(t)-xi(t-1)]+c1r1[Pi-xi(t)]+c2r2[Pg-xi(t)]+c3r3[?Xc+(1-?)Pc-xi(t)]

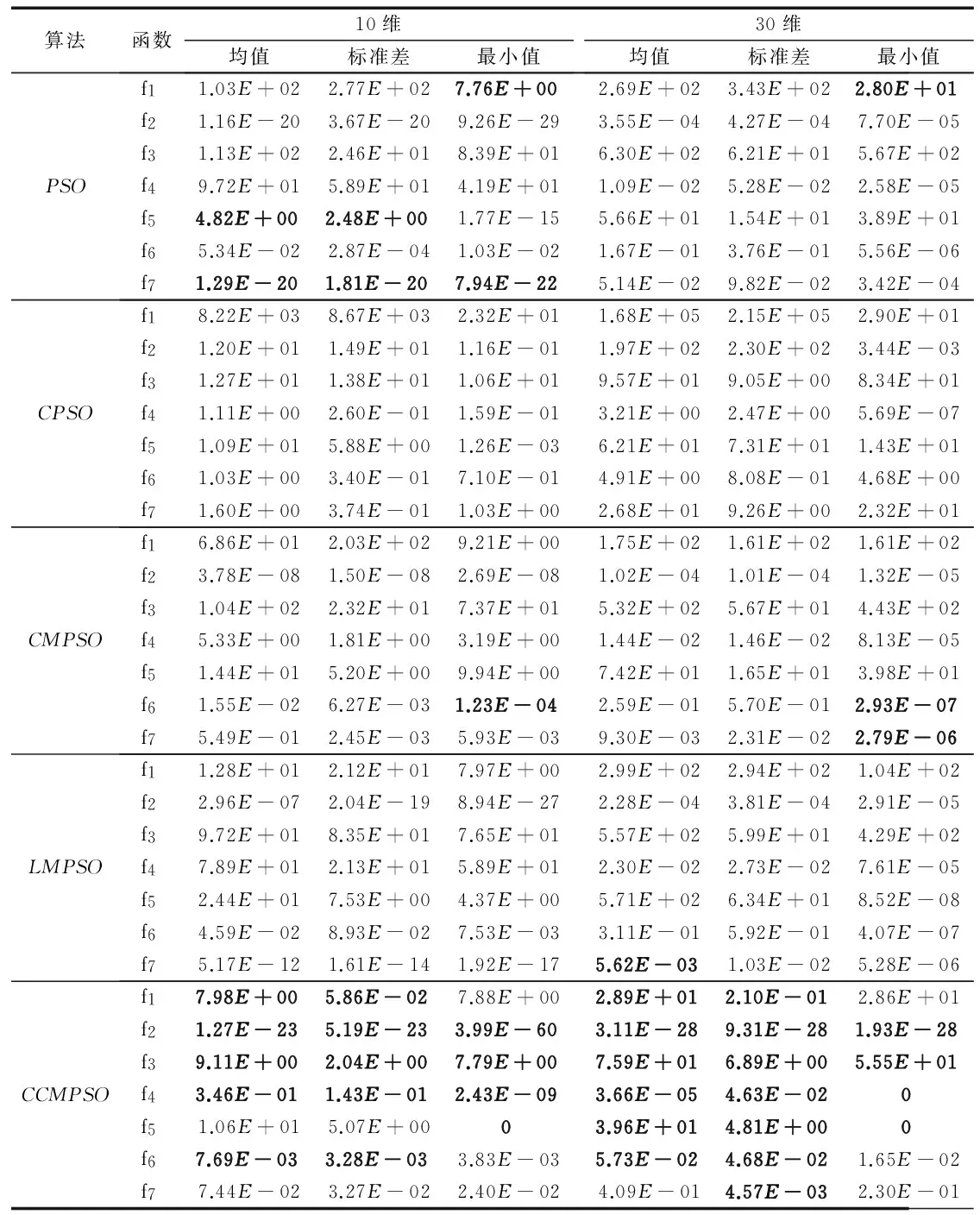
表3 各算法仿真結果 Fig. 3 Simulation results of algorithms

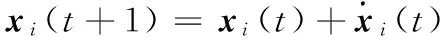
c2r2[Pg-xi(t)]+c3r3[?Xc+(1-?)Pc-xi(t)]

設φ1=c1r1,φ2=c2r2,φ3=c3r3,φ=φ1+φ2+φ3，PQ={φ1Pi+φ2Pg+φ3[?Xc+(1-?)Pc]}/φ，則:

(20)

式(20)是CCMPSO算法的控制方程，接下來使用李雅普諾夫第二方法推導算法的穩定性。

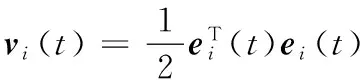
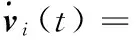
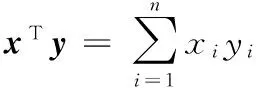
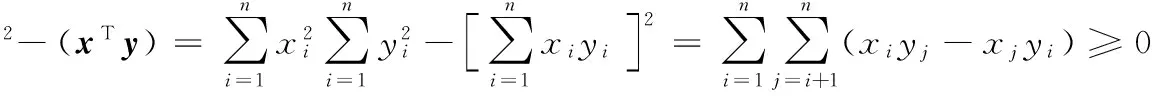
可得xTy≤‖x‖‖y‖，因此有:

[xi(t)-xi(t-1)]Tei(t)≤ ‖xi(t)-xi(t-1)‖T‖ei(t)‖

所以:

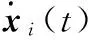
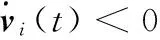
ω‖xi(t)-xi(t-1)‖-φ‖PQ-x(t)‖≤0

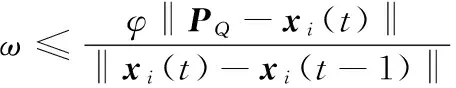
各算法在求解測試函數時的收斂情況如圖2～8所示。

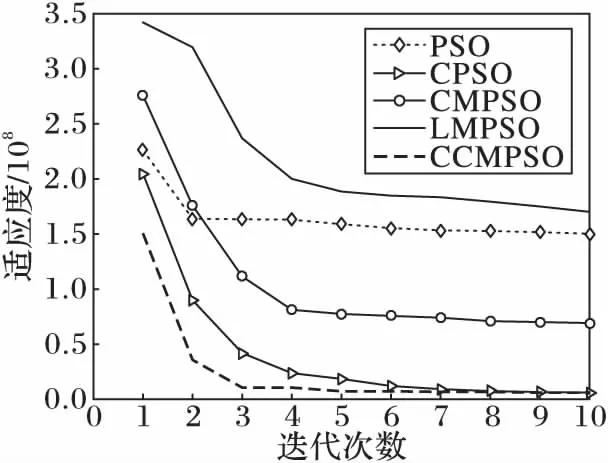
圖2 f1的收斂曲線Fig. 2 Convergence curve of f1

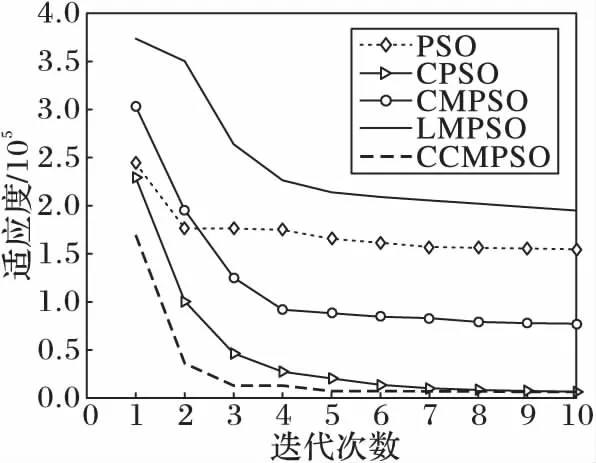
圖3 f2的收斂曲線Fig. 3 Convergence curve of f2

從圖2，3，5中可以看出，CCMPSO和CPSO具有較好的尋優能力，可以在規定的迭代次數內收斂到最優值，而且盡管最后收斂精度相差無幾，但是CCMPSO的收斂速度要更快于CMPSO。從圖4，7可以看出，對于f3、f6函數，在算法迭代初期，CCMPSO比CPSO稍微遜色，但是CCMPSO的收斂效果在短時間內可以迅速趕上和反超CPSO，最終的收斂精度也要優于后者，具有較好的尋優能力；而PSO、CMPSO和LMPSO則陷入局部最優，導致算法停滯。在圖8中，對于函數f7，CCMPSO算法可以迅速收斂到最優值。通過圖6可以看出，在測試f5函數時CPSO可以在算法前期快速收斂到1 400附近，但是隨后會在5～60左右的迭代次數內陷入局部極值，使得算法耗費了大量的時間；而CCMPSO盡管在初期0～20左右的迭代次數內收斂較慢，但是隨后可以迅速跳出局部極值，且可以持續保持較快的收斂速度直到尋找到全局最優，最終的收斂精度也優于CPSO；而PSO、CMPSO和LMPSO盡管可以始終保持收斂狀態，但是收斂速度和收斂精度相比CCMPSO要遜色很多。

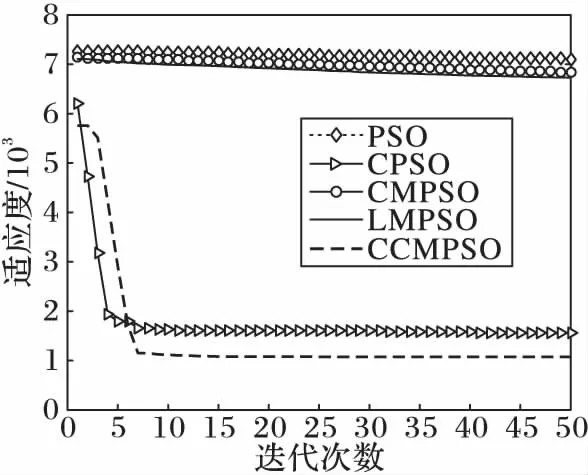
圖4 f3的收斂曲線Fig. 4 Convergence curve of f3

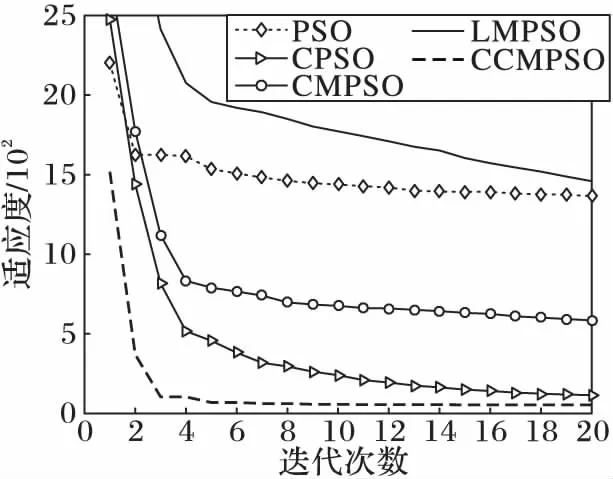
圖5 f4的收斂曲線Fig. 5 Convergence curve of f4

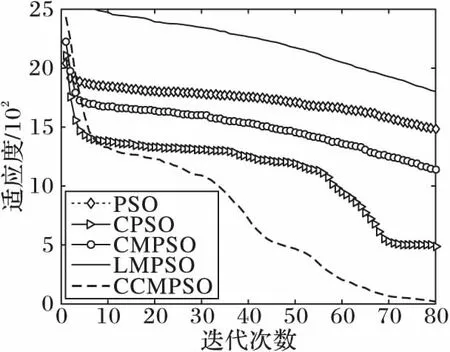
圖6 f5的收斂曲線Fig. 6 Convergence curve of f5

綜合實驗結果和分析過程，本文提出的CCMPSO算法是一種有效、快速和穩定的PSO改進算法。

從f1～f7的收斂圖像中可以明顯看出，CCMPSO算法的收斂效果呈現相對較好的態勢。除此之外，結合了質心思想的CPSO算法的收斂曲線，始終最靠近CCMPSO的收斂曲線，其次是引入柯西變異策略的CMPSO算法。因此可以得出結論，在結合了質心思想和柯西變異策略的CCMPSO算法中，質心算子對CCMPSO算法的貢獻度最高，柯西變異算子次之，混沌初始化算子的貢獻度最低。

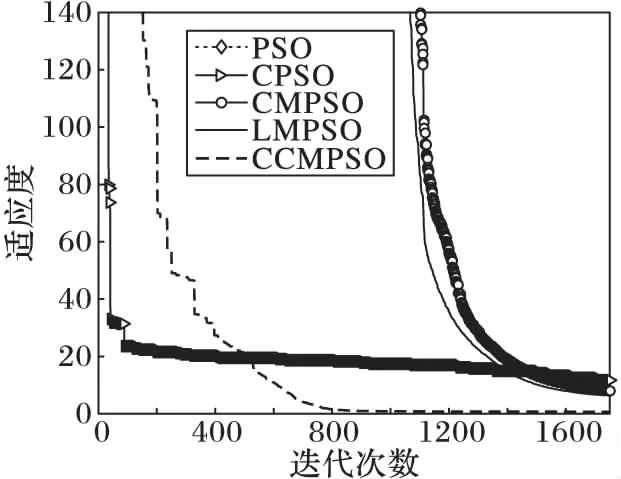
圖7 f6的收斂曲線Fig. 7 Convergence curve of f6

4 結語

本文為解決傳統粒子群算法收斂精度不高的問題，提出了一種混合的粒子群優化算法，該算法在融合了質心策略和柯西變異算法的基礎上,引進了Logistic混沌初始化策略，提高了初始種群的質量，并根據種群多樣性對慣性權重進行了動態調整，有效平衡了種群的在不同階段的全局尋優能力和局部挖掘能力。最后在對比測試和實驗分析階段，通過與標準PSO和其他幾種改進PSO算法的比較，本算法呈現出較好的仿真結果，算法的收斂精度有了明顯提升，通過標準差參數可以說明算法同樣具有較高的穩定性，但是依然存在陷入局部最優的可能。進一步的研究工作將主要圍繞如何降低算法的時間復雜度以及進一步提高算法的收斂精度方面展開。

References)

[1] KENNEDY J,EBERHART R C.Particle swarm optimization[C]// Proceedings of the 1995 IEEE International Conference on Neural Networks. Washington, DC: IEEE Computer Society, 1995:1942-1948.

[2] SHIYH.EBERHART R C.A modified particle swarm optimizer [C]// Proceedings of the 1998 IEEE International Conference on Evolutionary Computation. Piscataway, NJ: IEEE, 1998:67-73.

[3] CAMPOS M, KROHLING R A. Hierarchical bare bones particle swarm for solving constrained optimizationproblems [C]// Proceedings of the 2013 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2013: 805-812.

[4] CAMPOS M, KROHLING R A. Bare bones particle swarm with scale mixture of Gaussians for dynamic constrained optimization [C]// Proceedings of the 2014 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2014: 202-209.

[5] ZHANG Y, GONG D, HU Y, et al. Feature selection algorithm based on bare bones particle swarm optimization [J].Neurocomputing, 2015,148:150-157.

[6] 曹春紅,王利民,趙大哲,等.基于小生境改進粒子群算法的幾何約束求解[J]. 儀器儀表學報, 2012,33(9):2125-2129.(CAO C H, WANG L M, ZHAO D Z, et al.Geometric constraint solving based on niche improved particle swarm optimization[J].Chinese Journal of Scientific Instrument,2012,33(9):2125-2129.)

[7] 唐賢倫,張衡,李進,等. 基于多 Agent 粒子群優化算法的電力系統經濟負荷分配[J].電力系統保護與控制,2012, 40(10): 42-47.(TANG X L, ZHANG H, LI J,et al.Multiple Agent particle swarm algorithm based economic load distribution in power system[J]. Power System Protection and Control,2012,40(10):42-47.)

[8] KOSHTI A, ARYA L D, CHOUBE S C. Voltage stability constrained distributed generation planning using modified bare bones particle swarm optimization[J].Journal of the Institution of Engineers (India) Series B (Electrical, Electronics & Telecommunication and Computer Engineering), 2013,94(2):123-133.

[9] CHEN W N, ZHANG J, LIN Y, et al.Particle swarm optimization with an aging leader and challengers [J].IEEE Transactions on Evolutionary Computation,2013,17(2):241-258.

[10] SHI Y, EBERHART R. A modified particle swarm optimizer[C]// Proceedings of the1998 IEEE Conference on Evolutionary Computation. Piscataway, NJ: IEEE, 1998: 69-73.

[11] 介婧,曾建潮,韓崇昭.基于群體多樣性反饋控制的自組織微粒群算法[J].計算機研究與發展,2008,45(3):464-471. (JIE J,ZENG J C,HAN C Z. Self-organized particle swarm optimization based on feedback control of diversity [J].Journal of Computer Research and Development,2008,45(3):464-471.)

[12] 湯可宗,柳炳祥,楊靜宇,等.雙中心粒子群優化算法[J].計算機研究與發展,2012,49(5):1086-1094. (TANG K Z, LIU B X, YANG J Y, et al. Double center particle swarm optimization algorithm[J]. Journal of Computer Research and Development, 2012,49(5):1086-1094.)

[13] 趙新超,劉國蒞,劉虎球,等.基于非均勻變異和多階段擾動的粒子群優化算法[J].計算機學報,2014,37(9):2058-2068. (ZHAO X C, LIU G L, LIU H Q, et al. Particle swarm optimization algorithm based on non-uniform mutation and multiple stages perturbation [J].Chinese Journal of Computers, 2014,37(9):2058-2068.)

[14] 劉朝華,張英杰,章兢,等.一種雙態免疫微粒群算法[J].控制理論與應用, 2011, 28(1):65-72. (LIU C H, ZHANG Y J, ZHANG J, et al. A novel binary-state immune particle swarm optimization algorithm[J].Control Theory and Applications, 2011, 28(1):65-72.)

[15] 邱飛岳,莫雷平,江波,等.基于大規模變量分解的多目標粒子群優化算法研究[J].計算機學報,2015,38(12):2598-2613.(QIU F Y, MO L P, JIANG B,et al. Multi-objective particle swarm optimization algorithm using large scale variable decomposition[J].Chinese Journal of Computers,2015,38(12):2598-2613.)

[16] 劉建平.基于混沌和差分進化的混合粒子群優化算法[J].計算機仿真,2012,29(2):208-212.(LIU J P. Hybrid particle swarm optimization algorithm based on chaos and differential evolution[J].Journal of Computer Simulation, 2012,29(2):208-212.)

[17] 汪永生,李均利.質心粒子群優化算法[J].計算機工程與應用,2011,47(3):34-37.(WANG Y S,LI J L.Centroid particle swarm optimization algorithm[J].Computer Engineering and Applications,2011,47(3):34-37.)[18] 康嵐蘭,董文永,田降森.一種自適應柯西變異的反向學習粒子群優化算法[J].計算機科學,2015,42(10):226-231.(KANG L L,DONG W Y,TIAN J S. A novel particle swarm optimization algorithm with adaptive Cauchy mutation[J]. Computer Science, 2015,42(10):226-231.)

[19] 黃澤霞,俞攸紅,黃德才.慣性權重自適應調整的量子粒子群優化算法[J].上海交通大學學報,2012,46(2):228-232.(HUANG Z X, YU Y H, HUANG D C.Quantum behaved particle swarm algorithm withself adapting adjustment of inertia weight[J]. Journal of Shanghai Jiao Tong University, 2012,46(2):228-232.)

[20] KROHLING R A, MENDEL E. Bare bones particle swarm optimization with Gaussian or Cauchy jumps[C]// Proceedings of the 11th IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2009: 3285-3291.

[21] 相榮榮.協同量子粒子群優化及其應用研究[D].西安: 西安電子科技大學,2012:17-30. (XIANG R R. Cooperative quantum-behaved particle swarm optimization and its applications [D]. Xi’an: Xidian University, 2012: 17-30.)

[22] 陳世明,方華京.大規模智能群體的建模與穩定性分析[J].控制與決策,2005,20(5):490-494. (CHEN S M, FANG H J. Modeling and stability analysis of large-cale intelligent swarm [J]. Control and Decision,2005, 20(5):490-494.)

This work is partially supported by the Special Funds for the Research of Science and Technology Innovation Talent of Harbin Municipal Science and Technology Bureau (2015RAQXJ040), the Practice Innovation Team from Harbin Normal University in 2016 (Innovation Team of Mobile Intelligent Terminal), the Innovation and Entrepreneurship Training Program for College Students in Heilongjiang Province in 2016 (201610231029).

LYU Liguo,born in 1993,M. S. candidate.His research interests include group intelligence.

JI Weidong,born in 1978, Ph. D., associate professor.His research interests include neural network, swarm intelligence.

Improved particle swarm optimization algorithm combined centroid and Cauchy mutation

LYU Liguo, JI Weidong*

(CollegeofComputerScienceandInformationEngineering,HarbinNormalUniversity,HarbinHeilongjiang150025,China)

Concerning the problem of low convergence accuracy and being easily to fall into local optimum of the Particle Swarm Optimization (PSO), an improved PSO algorithm combined Centroid and Cauchy Mutation, namely CCMPSO, was proposed. Firstly, at the initialization stage, chaos initialization was adopted to improve the ability of initial particle uniform distribution.Secondly, the concept of centroid was introduced to improve the convergence rate and optimization capability. By calculating the global centroid of all the particles in the population and the individaual centroid formed by all of the individuals’ extreme values, sufficient information sharing could be realized in the interior of the particle swarm. To avoid falling into local optimal solution, Cauchy mutation operation was used to perturb the current optimal particle, in addition, the step length of disturbance was adaptively adjusted according to the operation rule of Cauchy mutation; the inertia weights were also dynamically adjusted according to population diversity. Finally, seven classical test functions were used to verify the algorithm. Experimental results indicate that the new algorithm has good performance in convergence precision of the function execution results, including the mean, the variance and the minimum value.

Particle Swarm Optimization (PSO); centroid; Cauchy mutation; population diversity; convergence accuracy

2016-08-01;

2016-10-11。 基金項目:哈爾濱市科技局科技創新人才研究專項資金資助項目(2015RAQXJ040);2016年哈爾濱師范大學實踐創新團隊(智能移動終端創新團隊)資助項目;2016年黑龍江省大學生創新創業訓練計劃項目(201610231029)。

呂立國(1993—)，男,江蘇徐州人,碩士研究生,主要研究方向：群體智能； 季偉東(1978—)，男,黑龍江哈爾濱人,副教授,博士,主要研究方向：神經網絡、群體智能。

1001-9081(2017)05-1369-07

10.11772/j.issn.1001-9081.2017.05.1369

TP181

A