基于人工螢火蟲局部決策域的改進生物地理學優化算法
王智昊,劉培玉,DING Ding
(1.山東師范大學 信息科學與工程學院,濟南 250014; 2.山東省分布式計算機軟件新技術重點實驗室,濟南 250014;3.Department of Mathematics, University of Padua, Padua 35100, Italy)
基于人工螢火蟲局部決策域的改進生物地理學優化算法
王智昊1,2,劉培玉1,2*,DING Ding3
(1.山東師范大學 信息科學與工程學院,濟南 250014; 2.山東省分布式計算機軟件新技術重點實驗室,濟南 250014;3.Department of Mathematics, University of Padua, Padua 35100, Italy)
(*通信作者電子郵箱liupy@sdnu.com)
針對生物地理學優化(BBO)算法搜索能力不足的缺點,提出基于螢火蟲算法局部決策域策略的改進遷移操作來提算法的全局尋優能力。改進的遷移操作能夠在考慮不同棲息地各自的遷入率與遷出率的基礎上,進一步利用棲息地之間的相互影響關系。將改進算法應用于12個典型的函數優化問題來測試改進生物地理學優化算法的性能,驗證了改進算法的有效性。與BBO、改進BBO(IBBO)、基于差分進化的BBO(DE/BBO)算法的實驗結果表明,改進算法提高了算法的全局搜索能力、收斂速度和解的精度。
生物地理學優化;遷移策略;螢火蟲算法;局部決策域;鄰域范圍
0 引言
生物地理學優化(Biogeography-Based Optimization, BBO) 算法是Simon受到生物地理學理論的啟發,在對生物物種遷移數學模型的研究基礎上,于2008年提出的一種新的智能優化算法[1]。該算法的基本思想來源于Wallace[2]在19世紀提出的生物地理學理論,該理論研究了生物物種棲息地的分布、遷移和滅絕規律。BBO算法自提出之后,已經得到了較廣泛的研究,BBO算法的理論分析、改進以及應用都取得了較好的研究成果:文獻[3]提出了混合遷移策略對BBO算法進行改進,提高了算法的收斂精度;文獻[4]提出了動態遷移策略,利用自適應約束方法來約束處理約束條件,更充分地利用了個體有效信息;文獻[5-6]利用馬爾可夫鏈模型對遷移模型進行分析,驗證不同的遷移率模型對算法性能產生重要影響,并得出符合自然規律的復雜遷移率模型的性能優于簡單的線性遷移率模型的性能的結論;文獻[7]提出一種新的變異算法來改進BBO算法,提高了算法的全局搜索與局部搜索能力;文獻[8-9]使用差分變異算法與BBO算法結合,利用差分變異算子的開采能力,有效改善BBO算法變異能力差的情況,避免陷入局部最優,從而增強了算法的全局搜索能力。為了進一步改進BBO算法的探測與搜索能力,本文將人工螢火蟲群優化(Glowworm Swarm Optimization, GSO) 算法的局部決策域策略引入BBO算法的遷移操作;并且,將改進的BBO算法與原始BBO算法及文獻[7-8]的改進算法作比較。實驗結果證明,本文提出的改進算法無論是探測能力還是搜索能力都能取得更好的結果。
1 生物地理學優化算法
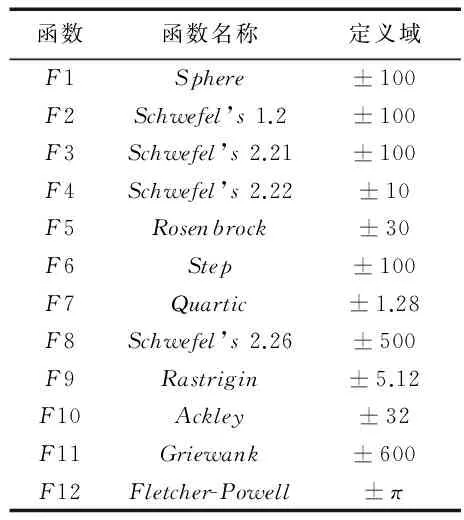
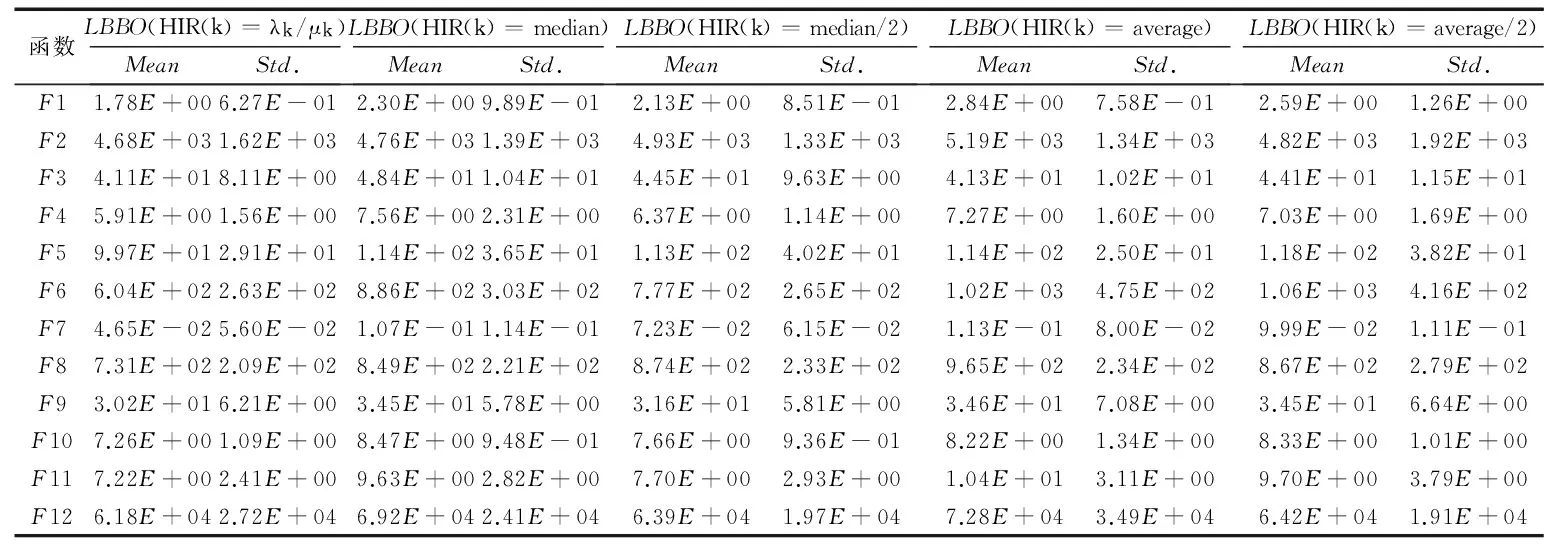
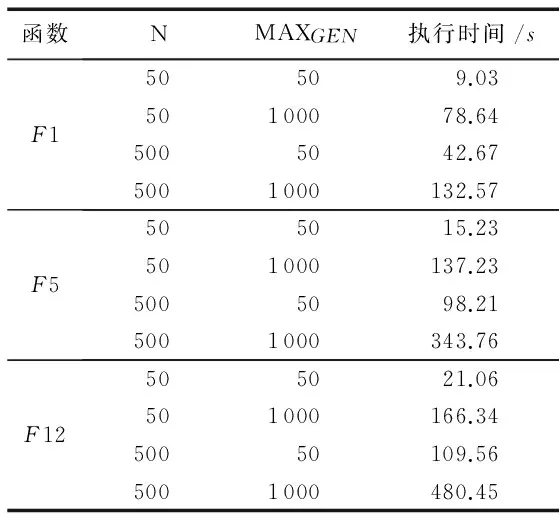
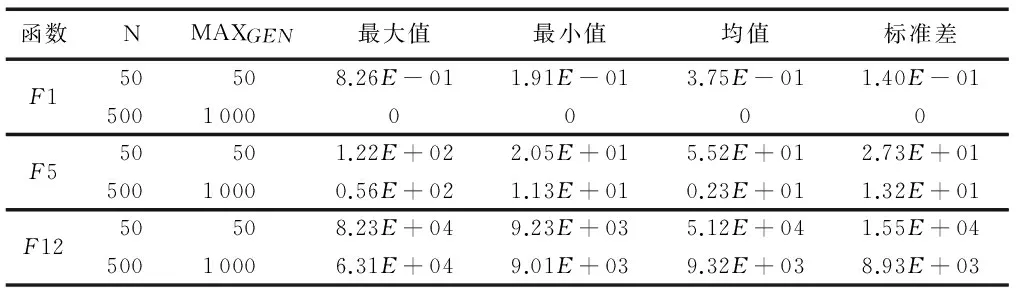
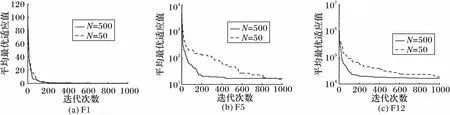
在生態系統中,每一個棲息地是否適合物種生存可以用棲息適宜指數(Habitat Suitability Index, HSI)來描述。一個棲息地的適宜指數可以由適宜指數變量(Suitability Index Variables, SIV)來表示,該變量用來描述與適宜指數相關的特征,例如棲息地的降水量、濕度、植被多樣性等。HSI與棲息地中物種的多樣性成正比。對于某一塊棲息地,假設它所能容納的最大物種數量為Smax,物種的遷入率為λ,其最大值為I,遷出率為μ,其最大值為E,并且假設E=I。當該棲息地物種數為0時,顯然,此時該棲息地物種的遷入率為最大值I。隨著物種的遷入,棲息地中物種數量增加,遷入率隨之減小而遷出率隨之增大,當棲息地中的物種數量達到所能容納的上限Smax時,由于棲息地已經達到飽和狀態,因此,遷入率下降為0,而此時遷出率達到最大值E。在圖(1)中,S1 有了對遷入率與遷出率的描述之后,可以計算某一時間段內棲息地中所存在的物種數量的概率Ps(t+Δt)。它表示t+Δt時刻棲息地包含s個物種的概率。計算公式如式(1)所示: Ps(t+Δt)=Ps(t)(1-λsΔt-μsΔt)+Ps-1λs-1Δt+Ps+1μs+1Δt (1) 其中:λs與μs分別表示當棲息地物種數量為s時的遷入率與遷出率。 根據圖遷入率與遷出率的線性關系,可得到物種數量為k時的遷入率與遷出率的計算方法,如式(2)與式(3)所示: λk=I(1-k/n) (2) μk=E(k/n) (3) 其中,n為棲息地可能存在的最大數目物種時的物種數量。由于假設棲息地物種的遷入率最大值與遷出率最大值相等,因此可得到λk+μk=E, 則當Δt→0時,可以將概率公式轉化為式(4)。如果一個棲息地存在物種數量概率較低,則該棲息地容易發生突變行為。也就是說,突變概率函數與該棲息地的存在物種數量概率成反比,因此可以得到相應的突變概率如式(5)所示。 (4) ms=mmax(1-Ps/Pmax) (5) 算法1 遷移算子。 end if end if end for output: solution of immigration() 算法2 突變算子。 input:initial population fori=1 toNdoPs(λi,μi) //根據式(1)計算存在物種數量概率Psms(Ps) end if end for output: solution of mutation() BBO是通過遷移操作實現可行解之間的信息共享的,棲息地中物種的數量正比于HSI。對于不同的棲息地之間的遷移運動而言,一塊棲息地發生遷入或遷出行為的概率與其遷入率或遷出率成正比。因此,將棲息地的遷入率的大小作為其是否發生遷入行為的判斷標準,進一步通過對其他棲息地的遷出率考察選擇從哪塊棲息地進行遷出操作。突變操作能夠使得低物種數量存在概率(existing probability of the number of species)的解具有一定的幾率突變為較好的解,防止算法陷入局部最優,可以增加解的多樣性。為了防止最優解被執行突變操作,可以采用精英策略,將每一代的最優解都保存到精英表中,參與到下一代的算法執行過程中。如何執行突變操作應該根據具體解決的問題進行設定。 在BBO算法中,遷移操作僅考慮棲息地各自的遷入率與遷出率大小來判斷如何執行遷移操作,并沒有考慮到棲息地之間的相互影響。所以,本文將GSO算法的局部決策域思想引入BBO算法的遷移操作,能夠增強算法的探測能力。GSO算法中的局部決策域策略能夠實現決策鄰域內個體間吸引關系的定量分析,通過計算棲息地之間的吸引度來判斷它們之間的吸引關系,能夠在遷入率與遷出率的基礎上更精確地執行遷移操作。 局部決策域策略的特點適合作為BBO中棲息地之間消息傳遞的輔助工具。在各個棲息地之間,待遷入的棲息地能夠吸引待遷出棲息地的物種。下面首先給出應用于BBO的局部決策域策略相關定義。 定義1 棲息地遷移矩陣。設棲息地數量為n,計算任意兩個棲息地之間的相似度S(Hi,Hj)(相似度可以是對稱的也可以是不對稱的),表示棲息地Hj吸引物種從棲息地Hi遷出并且遷入到棲息地Hj的可能性,并將Hi稱為待遷出棲息地,Hj稱為待遷入棲息地。棲息地之間的相似度組成的n×n的相似度矩陣S稱為棲息地遷移矩陣。S(Hi,Hj)按照式(6)計算: (6) 定義2 棲息地遷入參考度(Habit Immigration Reference, HIR)。相似度S(Hk,Hk)表示棲息地Hk能否成為待遷入棲息地的參考度,并將其記為HIR(k)(k=1,2,…,n)。HIR(k)的取值能夠影響待遷入棲息地與待遷出棲息地數量的比例,決定了LBBO的遷移操作能否有效地搜索到優化問題的全局最優解。 根據文獻[7]對參考度的定義可以得到,對于所有的棲息地,待遷入棲息地的數量正比于HIR(k)。對于任意棲息地Hk,根據式(1)可知,HIR(k)與遷入率λk成正比,與遷出率μk成反比。在本文中,令S(Hk,Hk)的取值為棲息地Hk遷入率λk與遷出率μk的比值λi/μk,并且在后面的仿真實驗中采用HIR(k)取值為相似度S的中值、均值、中值的一半以及均值的一半等取值方法作比較,討論如何選擇更優的HIR(k)取值方法。 定義3 棲息地吸引度(Habit Attraction Reference, HAR)。 將GSO算法思想引入BBO算法,GSO中Agent的蟲熒光素屬性可以視為BBO算法中任一棲息地對其他相鄰棲息地物種的吸引強度。令lHi(t)表示任意棲息地Hi在t時刻的HAR取值。在算法初始化時,令每一塊棲息地都具有相等的HAR值l0。HAR的更新公式如式(7)所示: lHi(t+1)=(1-ρ)lHi(t)+γSt+1(Hi,Hj) (7) 其中:lHi(t)表示棲息地Hi在t時刻的吸引度值;ρ(0<ρ≤1)為吸引度衰變常數;γ為吸引度增強常數;St(Hi,Hj)表示t時刻棲息地Hi的HIR值,由式(1)計算。 棲息地遷入參考度HIR反映一塊棲息地適合其他物種遷入的程度,HIR值越大則表明該棲息地適合其他物種遷入的程度越強,也就是說對其他棲息地的吸引度越強。對于任意棲息地Hi與Hj,其吸引度的更新需要考慮當前吸引度與遷入參考度HIR的雙重影響。 根據棲息地的HAR能夠確定物種的遷移方向,每一塊棲息地的物種都會向該棲息地鄰域范圍內其他吸引度更高的棲息地遷移。對于任意棲息地i,其物種向鄰域內棲息地j的遷移概率如式(8)所示: (8) 根據式(8)可以表明,物種選擇待遷入棲息地的概率是與其吸引度成正比的。 (9) 其中:β為常參數,nt為控制鄰居數量的參數。根據局部決策域策略為改進的BBO算法作出定義。 定義5 棲息地遷移策略Ω(l,r)。Ω(l,r):Hn→H用來控制LBBO遷移操作。通過計算l與r求得棲息地吸引度HAR值來判斷物種何時從待遷出棲息地Hi遷出并且遷入到待遷入棲息地Hj。 LBBO的棲息地遷移策略執行的基本流程如下所示。 1)對于任意棲息地,分別根據式(2)、式(3)與式(6)計算得到遷入率λ、遷出率μ以及棲息地相似度矩陣S,并根據λ與μ求得棲息地遷入參考度HIR(k),根據式(7)、式(8)與式(9)求得l、r與遷移概率。 2)根據式(7)與式(8)以及步驟1)所求得的HIR(k)、l、r與遷移概率計算并更新每一塊每塊棲息地的棲息地吸引度HAR。 3)將HAR值排序,選擇取值最大時所對應的棲息地Hi與棲息地Hj。 5)用SIVm隨機替換Hi的一個SIV。 定義6 棲息地突變策略M(λ,μ)。M(λ,μ):H→H通過棲息地物種數量存在概率Ps來確定隨機改變棲息地適宜度指數SIVm的棲息地突變操作,通過式(4)來計算。棲息地突變策略基本流程見BBO突變操作。 定義7 LBBO。LBBO={Φ,m,n,λ,μ,Ω,T}:Hn→Hn是一個八元組,能夠將已經初始化的棲息地進行迭代優化。其中Φ=?→{Hn,HSIn}是初始化一組棲息地,并且計算棲息地的HSI值的函數。T=Hn(True,False)是算法終止的判定標準。 LBBO的偽代碼如算法3所示。 算法3 LBBO算法。 input:initial population forg=1 toMAXGENdo fori=1toNdoCalculateλi,μi,HIR,HAR end for fori=1toNdo end for mutation() //根據算法2執行突變算子 end if end for end for output: best solutions 4.1 測試函數 在本文中,通過benchmark函數優化問題來比較LBBO與基本BBO性能。為了提高實驗結果的可靠性,選取了在函數極值個數、極值點分布方面有代表性的7個單峰函數Sphere function、Schwefel’s Problem 1.2、Schwefel’s Problem 2.21、Schwefel’s Problem 2.22、Rosenbrock function、Step function、Quartic function與5個多峰函數Schwefel’s Problem 2.26、Rastrigin function、Ackley function、Griewank function、Fletcher-Powell function作為測試函數[11]。為了描述方便將其標記為F1~F12,如表1所示。其中,F1與F7~F8為分段函數,F1、F2、F5~F7以及F10與F12為正則函數。 表1 測試函數Tab. 1 Benchmark functions 4.2 LBBO算法性能分析 4.2.1 實驗參數設置 為了比較LBBO算法與基本BBO算法及兩種改進BBO算法的性能,種群規模及執行代數均按照文獻[1]進行設置,令棲息地最大物種數N=50; 每個函數運行代數MAXGEN=50。 4.2.2 實驗結果與分析 實驗結果如表2所示。對于單峰函數F1~F7,通過對實驗結果的觀察可以發現,各項指標LBBO均優于BBO算法及其他兩種改進算法。對于函數F5,是非凸的病態函數,其全局最優點位于一個平滑、狹長的拋物線形山谷內,其最優點較難求得。而LBBO采用了局部決策域策略,能夠通過不同解之間的相互吸引關系較為準確的判斷全局最優解。并且除了函數F3外,LBBO運算30次所得到結果的標準差也小于BBO,表明LBBO在求解函數F1、F2以及F4~F7時更加穩定。對于函數F3,通過對實驗結果觀察可以發現,LBBO在求解過程中與BBO算法及其他兩種算法相比,大部分最優解的取值與均值差距較大。 表2 F1~F12函數30次獨立實驗平均結果比較Tab. 2 Comparison of benchmark functions F1~F12 averaged over 30 independent runs 對于多峰函數F8~F12,優化結果LBBO算法優于BBO算法與其他兩種比較算法。其中,函數F9峰形呈高低起伏不定跳躍性的出現, 因此,LBBO中的吸引子策略能夠通過遷移信息在解之間的傳播而比較有效地發現函數最優解。函數F10十分復雜,優化過程中易落入局部最優的陷阱。LBBO采用局部決策域策略,能夠在算法陷入局部最優時使得算法在一定概率下接受較差解,使得算法具有更強的跳出局部最優的能力。因此LBBO能夠較準確地得到函數F10優化問題的最優解。函數F11具有許多局部極小值,較難求得全局最優點,LBBO從全局搜索與局部搜索兩個方面對該復雜函數進行優化,具有更強的全局尋優能力與跳出局部最優的能力,所以LBBO能夠非常有效地求解函數F11這樣的復雜函數。 4.3 LBBO的HIR參數取值分析實驗 4.3.1 實驗設置 LBBO的吸引子策略HIR取值為棲息地遷入率與棲息地遷出率的比值,為了比較HIR不同取值情況下算法的效率設置對比實驗。分別令HIR取值為棲息地遷入率與遷出率的比值、棲息地相似度矩陣S的中值(median)、棲息地相似度矩陣S中值的一半、棲息地相似度矩陣S的均值以及棲息地相似度矩陣均值的一半,采用4.1節所示12種測試函數,通過30次獨立測試結果的均值與標準差來比較算法的效率。五種HIR取值方法的LBBO的參數按照4.2.1節進行設置,令棲息地遷移概率Pmod,突變概率m=0,精英棲息地數量K=2,最大遷移率設置為E=I=1,最大突變率mmax,初始HARl0=5,初始決策域半徑=1; 棲息地最大物種數N=50; 每個函數運行代數MAXGEN=50。 4.3.2 實驗結果與分析 實驗結果如表3與表4所示,通過觀察表3數據可以發現在12個函數求解中LBBO(HIR(k)=λk/μk)效果要優于其他4種情況。主要原因是棲息地相似度矩陣S僅考慮了單一棲息地對遷移操作的影響,而遷入率與遷出率則綜合考慮了兩個棲息地之間的相互關系,因此HIR的值設置為棲息地遷入率與遷出率的比值能夠更好地利用棲息地物種數量信息,在棲息地之間傳遞吸引度與歸屬度信息時能夠更加準確地指導棲息地間物種遷移行為。 表3 LBBO算法不同的HIR取值求解測試函數比較Tab. 3 Comparison of efficiency with different values of HIR for LBBO algorithm 4.4 LBBO初始種群與迭代次數參數分析實驗 4.4.1 實驗設置 為了分析算法的初始最大物種數以及算法執行代數對算法效果的影響,在實驗設置中均采用較大數值來分析較大取值的物種數及執行代數是否能對算法效果帶來明顯的影響。采用4.1節所示F1、F5、F12等3個測試函數,通過30次獨立測試結果的均值與標準差來比較算法的效率。棲息地最大物種數N=500; 每個函數運行代數MAXGEN=1 000,其他參數設置與4.2.1節相同。 4.4.2 實驗結果與分析 對于簡單的單峰函數F1與復雜的多峰函數F5與F12增大物種數與執行代數后能夠取得最優值。對于測試函數F1,表4與圖1(a)中顯示在算法執行600代之前隨著種群規模的增大算法的精確度會略微增加,但是600代之后基本上沒有差異。對于F5由圖1(b)可知在算法迭代800代之前初始種群數量對算法的結果有著顯著影響。圖1(c)表明相對F5更加復雜的函數F12在迭代1 000代初始種群的規模才開始不明顯。根據這一實驗結果可以得出,測試函數的復雜程度與其對初始種群規模的敏感正度是成正比的,對于簡單函數而言更大的初始種群沒有很明顯的影響。 表4 F1、F5與F12的LBBO算法時間Tab. 4 Time of LBBO algorithm for solving F1, F5 and F12 對于執行代數而言,從圖1中觀察可知在一定數量的代數之后精度幾乎不再提升,其主要原因是,算法能否求得最優值主要取決于算法跳出局部最優的能力。算法迭代次數的增加無疑會對算法執行時間造成很大影響,然而,如表5所示,執行代數相同時初始種群的規模對算法執行時間的影響更加明顯。這是因為初始種群規模增加會使得遷入遷出率、HIR等參數的計算次數激增而顯著地增加算法執行時間。因此對于算法在實際問題的應用應該通過大量實驗考察初始種群規模與迭代次數在何時無法對算法的精度帶來提升,進而選擇恰當的取值來平衡算法精度與算法效率的關系。 表5 LBBO算法不同最大物種數與執行代數求解測試函數效果比較Tab. 5 Comparison of results with different values of N and MAXGEN 圖1 LBBO算法不同最大物種數與迭代次數求解測試函數的收斂對比曲線Fig. 1 Convergence curve of test functions of LBBO with different N and MAXGEN 本文提出了一種基于局部決策域策略的LBBO算法,采用螢火蟲算法局部決策域策略來改進算法的局部搜索能力。通過對LBBO算法在12個基準函數的測試結果分析,該算法能夠較好地求解函數極值優化問題。通過與BBO算法的比較,可以發現LBBO的性能明顯優于原始算法。當然,BBO算法的研究與其他進化算法(Evolutionary Algorithm, EA)(例如遺傳算法(Genetic Algorithm, GA)、粒子群優化(Particle Swarm Optimization, PSO)算法等)相比仍處于較初級的研究階段。在今后的工作中,將嘗試利用其他的算法框架模型(例如文化算法框架模型)來改進BBO的性能。 References) [1] SIMON D. Biogeography-based optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(6): 702-713. [2] WALLACE A R. The Geographical Distribution of Animals: with a Study of the Relations of Living and Extinct Faunas as Elucidating the Past Changes of the Earth’s Surface[M]. Cambridge: Cambridge University Press, 2011:15-25. [3] 畢曉君, 王玨. 基于混合遷移策略的生物地理學優化算法[J]. 模式識別與人工智能, 2012, 25(5):768-774.(BI X J, WANG J. Biogeography-based optimization based on hybrid migration strategy[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(5):768-774.) [4] 畢曉君, 王玨, 李博,等. 基于動態遷移的ε約束生物地理學優化算法[J]. 計算機研究與發展, 2014, 51(3):580-589.(BI X J, WANG J, LI B, et al. An ε constrained biogeography-based optimization with dynamic migration[J]. Journal of Computer Research and Development, 2014, 51(3):580-589.) [5] MA H, SIMON D. Analysis of migration models of biogeography-based optimization using Markov theory [J]. Engineering Applications of Artificial Intelligence, 2011, 24(6): 1052-1060. [6] MA H, SIMON D, FEI M, et al. Variations of biogeography-based optimization and Markov analysis[J]. Information Sciences, 2013, 220(1): 492-506. [7] YANG G P, LIU S Y, ZHANG J K, et al. Control and synchronization of chaotic systems by an improved biogeography-based optimization algorithm[J]. Applied Intelligence, 2013, 39(1): 132-143. [8] BHATTACHARYA A, CHATTOPADHYAY P K. Hybrid differential evolution with biogeography-based optimization for solution of economic load dispatch[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1955-1964. [9] 葉開文, 劉三陽, 高衛峰. 基于差分進化的生物地理學優化算法[J]. 計算機應用, 2012, 32(11):2981-2984.(YE K W, LIU S Y, GAO W F. Biogeography-based optimization algorithm of differential evolution [J]. Journal of Computer Applications, 2012, 32(11):2981-2984.) [10] KRISHNANAND K N, GHOSE D. Glowworm swarm optimization: a new method for optimizing multi-modal functions[J]. International Journal of Computational Intelligence Studies, 2009, 1(1): 93-119. [11] YAO X, LIU Y, LIN G. Evolutionary programming made faster [J]. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102. This work is partially supported by National Natural Science Foundation (61373148, 61502151), the Shandong Province Natural Science Foundation (ZR2014FL010), the Shandong Province Social Science Project (2012BXWJ01, 15CXWJ13, 16CFXJ05). WANG Zhihao, born in 1986, Ph.D. candidate. His research interests include intelligence algorithms. LIU Peiyu, born in 1960, professor. His research interests include information security. DING Ding, born in 1987, Ph. D. candidate. His research interests include network security. Improved biogeography-based optimization algorithm based on local-decision domain of glowworm swarm optimization WANG Zhihao1,2, LIU Peiyu1,2*, DING Ding3 (1.SchoolofInformationScienceandEngineering,ShandongNormalUniversity,JinanShandong250014,China;2.ShandongProvincialKeyLaboratoryforDistributedComputerSoftwareNovelTechnology,JinanShandong250014,China;3.DepartmentofMathematics,UniversityofPadua,Padua35100,Italy) Aiming at the lack of searching ability of Biogeography-Based Optimization (BBO) algorithm, an improved migration operation based on local-decision domain was proposed to improve the global optimization ability of the algorithm. The improved migration operation can further utilize the interaction between habitats in consideration of the respective migration rates and evapotranspiration rates of different habitats. The improved algorithm was applied to 12 typical function optimization problems to test the performance, and the effectiveness of the improved algorithm was verified. Compared with BBO, Improved BBO (IBBO) and Differential Evolution/BBO (DE/BBO), the experimental results show that the proposed algorithm can improve the capacity of global searaching optimal solution, convergence speed and computational precision of solution. Biogeography-Based Optimization (BBO); migration operation; Glowworm Swarm Optimization (GSO); local-decision domain; neighborhood range 2016-10-16; 2016-12-01。 基金項目:國家自然科學基金資助項目(61373148, 61502151);山東省自然科學基金資助項目(ZR2014FL010);山東省社會科學規劃項目(2012BXWJ01,15CXWJ13,16CFXJ05)。 王智昊(1986—),男,山東濟南人,博士研究生,主要研究方向:智能算法; 劉培玉(1960—),男,山東臨朐人,教授,CCF會員,主要研究方向:信息安全; DING Ding(1987—),男,山東濟南人,博士研究生,主要研究方向:網絡安全。 1001-9081(2017)05-1363-06 10.11772/j.issn.1001-9081.2017.05.1363 TP18 A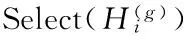
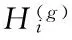
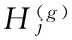
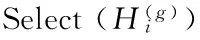
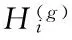
2 人工螢火蟲優化算法
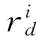
3 基于局部決策域策略的改進BBO算法
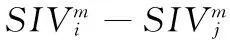
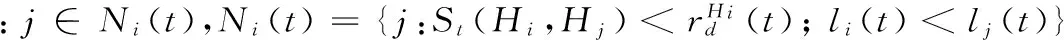
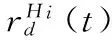
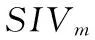
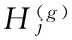
4 實驗研究
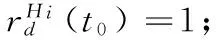

5 結語

