變異蝙蝠算法求解折扣{0-1}背包問(wèn)題

吳聰聰，賀毅朝，陳嶷瑛，劉雪靜，才秀鳳

(河北地質(zhì)大學(xué) 信息工程學(xué)院,石家莊 050031)

變異蝙蝠算法求解折扣{0-1}背包問(wèn)題

吳聰聰*，賀毅朝，陳嶷瑛，劉雪靜，才秀鳳

(河北地質(zhì)大學(xué) 信息工程學(xué)院,石家莊 050031)

(*通信作者電子郵箱hebwucongcong@126.com)

針對(duì)確定性算法難于求解規(guī)模大、數(shù)據(jù)范圍廣的折扣{0-1}背包問(wèn)題(D{0-1}KP)，提出了基于蝙蝠算法的快速求解D{0-1}KP的變異蝙蝠算法(MDBBA)。首先，利用雙重編碼解決D{0-1}KP的編碼問(wèn)題；其次，將貪心修復(fù)與優(yōu)化算法(GROA)應(yīng)用于蝙蝠個(gè)體適應(yīng)度計(jì)算中，使算法快速得到有效解；然后，選擇使用差分演化(DE)的變異策略提高算法的全局尋優(yōu)能力；最后，蝙蝠個(gè)體按一定概率進(jìn)行Lévy飛行，增強(qiáng)算法探索能力和跳出局部極值的能力。對(duì)四類(lèi)大規(guī)模實(shí)例的仿真計(jì)算表明：MDBBA非常適于求解大規(guī)模的D{0-1}KP，比第一遺傳算法(FirEGA)和雙重編碼蝙蝠算法(DBBA)求得的最優(yōu)值和平均值都更優(yōu)，MDBBA收斂速度明顯快于DBBA。

折扣{0-1}背包問(wèn)題；蝙蝠算法；差分演化；Lévy飛行；貪心策略；非正常編碼

0 引言

折扣{0-1}背包問(wèn)題(Discounted {0-1}Knapsack Problem, D{0-1}KP)是經(jīng)典0-1背包問(wèn)題的一個(gè)擴(kuò)展形式[1-4]，其思想源于商業(yè)領(lǐng)域的打折，在項(xiàng)目決策、投資和預(yù)算控制等方面具有廣闊的應(yīng)用背景[2]。基于動(dòng)態(tài)規(guī)劃求解D{0-1}KP的確定性算法是偽多項(xiàng)式時(shí)間的[1-2,4]，當(dāng)問(wèn)題規(guī)模較大并且各項(xiàng)的價(jià)值系數(shù)與重量系數(shù)在較大范圍內(nèi)取值時(shí)，耗費(fèi)大量的求解時(shí)間，缺乏實(shí)用性。 因此，探討利用進(jìn)化算法快速求解D{0-1}KP的可行方法是一個(gè)值得研究的問(wèn)題。

目前，D{0-1}KP的研究成果還相對(duì)較少，其中Guldan[1]首先提出了D{0-1}KP 問(wèn)題，給出了D{0-1}KP的一個(gè)數(shù)學(xué)模型，并基于動(dòng)態(tài)規(guī)劃給出了一個(gè)精確算法；Rong等[2]研究了D{0-1}KP 的核(Core)問(wèn)題，并將動(dòng)態(tài)規(guī)劃與核相結(jié)合求解D{0-1}KP；賀毅朝等[3]給出了D{0-1}KP的兩個(gè)新的數(shù)學(xué)模型，并基于精英保留策略遺傳算法(Elitist Genetic Algorithm, EGA)提出了求解D{0-1}KP兩個(gè)算法：第一遺傳算法(First Genetic Algorithm, FirEGA)和第二遺傳算法(Second Genetic Algorithm, SecEGA)；隨后，又在文獻(xiàn)[4]中給出了一系列的求解算法。

本文基于新型啟發(fā)式算法——蝙蝠算法(Bat Alogrithm, BA)[5]求解D{0-1}KP，首先提出利用雙重編碼的二進(jìn)制蝙蝠算法(Double codes Binary Bat Algorithm，DBBA)[6]求解D{0-1}KP；為了消除求解過(guò)程中產(chǎn)生的不可行解，利用文獻(xiàn)[3]中貪心修復(fù)與優(yōu)化算法(Greedy Repair and Optimization Algorithm, GROA)對(duì)蝙蝠個(gè)體進(jìn)行修復(fù)和優(yōu)化處理并計(jì)算適應(yīng)度。然后，為進(jìn)一步提高算法的求解精度和收斂速度提出了變異蝙蝠算法(Mutated Double Codes Binary Bat Algorithm，MDBBA)。在DBBA基礎(chǔ)上，加入差分演化的變異策略來(lái)提高種群的多樣性，以增強(qiáng)算法的全局尋優(yōu)能力；同時(shí)，讓每只蝙蝠按照50%的概率進(jìn)行Lévy飛行，以避免算法陷入局部最優(yōu)。最后，對(duì)四類(lèi)大規(guī)模D{0-1}KP實(shí)例的計(jì)算結(jié)果表明：對(duì)于大規(guī)模的D{0-1}KP 實(shí)例，MDBBA能夠快速求得一個(gè)近似比接近于1的近似解，其效果優(yōu)于FirEGA[3]和DBBA。

1 D{0-1}KP定義

定義[1]給定n個(gè)均含有3個(gè)項(xiàng)(或物品)的項(xiàng)集，項(xiàng)集i(0≤i≤n-1)中含有的3個(gè)項(xiàng)分別記為3i,3i+1,3i+2，其中前兩項(xiàng)具有的價(jià)值系數(shù)分別為v3i和v3i+1，具有的重量系數(shù)分別為w3i和w3i+1；前兩項(xiàng)合并到一起構(gòu)成第三項(xiàng)3i+2，它具有的價(jià)值系數(shù)為v3i+2=v3i+v3i+1，具有的折扣重量系數(shù)為w3i+2，滿足w3i+2w3i，w3i+2>w3i+1。對(duì)于每個(gè)項(xiàng)集i(0≤i≤n-1)，項(xiàng)3i,3i+1,3i+2最多有一個(gè)被選中裝入背包中。如何選擇各項(xiàng)裝入背包，使得被裝入背包的所有項(xiàng)的重量系數(shù)之和在不超過(guò)背包載重C的前提下價(jià)值系數(shù)和最大？

Guldan給出了D{0-1}KP的第一個(gè)數(shù)學(xué)模型，描述如下：

(1)

s.t.x3i+x3i+1+x3i+2≤1;i=0,1,…,n-1

(2)

(3)

x3i,x3i+1,x3i+2∈{0,1},i=0,1,…,n-1

(4)

其中: 二元變量xj(0≤i≤3n-1)表示項(xiàng)j是否被裝入背包中，即xj=1表示第j項(xiàng)被裝入了背包中，xj=0表示第j項(xiàng)未被裝入背包。顯然，任意向量X=[x0,x1,x2,…,x3n-1]∈{0,1}3n僅僅表示D{0-1}KP的一個(gè)潛在解，只有當(dāng)它同時(shí)滿足了約束條件(2)和(3)時(shí)才是一個(gè)可行解。

2 雙重編碼的蝙蝠算法

蝙蝠算法(BA)是Yang[5]于2010年提出的一種新型啟發(fā)式算法，其思想源于蝙蝠尋找獵物過(guò)程中回聲定位原理。目前，該算法已引起國(guó)內(nèi)外學(xué)者的廣泛關(guān)注，成為計(jì)算智能研究領(lǐng)域的一個(gè)新的研究熱點(diǎn)，學(xué)者們不但對(duì)算法的性能進(jìn)行各種改進(jìn)[7-10]，并將其成功地應(yīng)用到工程設(shè)計(jì)[11-13]、分類(lèi)[14]、神經(jīng)網(wǎng)絡(luò)[15]和模糊聚類(lèi)[16]等領(lǐng)域。

蝙蝠算法是解決連續(xù)變量的函數(shù)優(yōu)化問(wèn)題，它將種群數(shù)量為N的蝙蝠飛行的位置映射成d維問(wèn)題空間中的N個(gè)解向量，通過(guò)蝙蝠種群飛行的過(guò)程來(lái)進(jìn)行問(wèn)題的優(yōu)化求解，用求解問(wèn)題的適應(yīng)度函數(shù)值來(lái)衡量每個(gè)蝙蝠的位置Xi=[xi1,xi2,…,xid]的好壞，每只蝙蝠在種群最優(yōu)解影響下飛行，直至達(dá)到全局最優(yōu)解。為了將蝙蝠算法應(yīng)用于折扣背包問(wèn)題求解，這里為每只蝙蝠設(shè)置了雙重編碼[6,17]，即針對(duì)每只蝙蝠的實(shí)數(shù)位置Xi引入一個(gè)的二進(jìn)制位置Bi=[bi1,bi2,…,bid]，映射關(guān)系如式(5)[6]：

(5)

其中xij∈[-1,1]是第i只蝙蝠在第j維的實(shí)數(shù)值。這樣每只蝙蝠可表示成一個(gè)二元組(Xi(t),Bi(t))，其中Xi(t)=[xi1(t),xi2(t),…,xid(t)] ∈[-1,1]d是第t代第i個(gè)蝙蝠的實(shí)數(shù)位置；Bi(t)=[bi1(t),bi2(t),…,bid(t)]∈{0,1}d是該蝙蝠的二進(jìn)制位置。蝙蝠的適應(yīng)度函數(shù)按它的二進(jìn)制位置計(jì)算f(Bi(t))，蝙蝠的實(shí)數(shù)位置Xi(t)按式(6)～(8)更新:

fi(t)=fmin+(fmax-fmin)*β

(6)

Vi(t+1)=Vi(t)+(Xi(t)-Y)*fi(t)

(7)

Xi(t+1)=Xi(t)+Vi(t)

(8)

其中:fi(t)∈[fmin,fmax]是第t代第i個(gè)蝙蝠的頻度;β∈[0,1]是隨機(jī)數(shù);Vi(t)是第t代第i個(gè)蝙蝠的飛行速度;Y是第t代蝙蝠群體最優(yōu)實(shí)數(shù)位置。

設(shè)(hXi(t),hBi(t))為第t代第i個(gè)蝙蝠的歷史最優(yōu)個(gè)體；(Y,P)為蝙蝠群最優(yōu)個(gè)體。下面以求解最大約束優(yōu)化問(wèn)題maxf(X)為例給出具有雙重編碼的二進(jìn)制蝙蝠算法(DBBA)[6]的描述。

算法1 DBBA[6]。

輸入 maxf(X)，最大迭代次數(shù)MaxIt;

輸出 最優(yōu)解P，適應(yīng)度函數(shù)值f(P)。

步驟1 隨機(jī)產(chǎn)生初始蝙蝠群實(shí)數(shù)位置，用式(3)計(jì)算得到蝙蝠的二進(jìn)制位置，令迭代次數(shù)t=0。

步驟2 設(shè)置每只蝙蝠的初始速度Vi，脈沖發(fā)射速率fi、脈沖響度ai和脈沖頻率ri的初始值。

步驟3 計(jì)算每只蝙蝠適應(yīng)度，令其歷史最好個(gè)體等于該蝙蝠個(gè)體，根據(jù)各個(gè)蝙蝠適應(yīng)值找出最好的蝙蝠Xk，令全局最優(yōu)等于該蝙蝠。

步驟4

While(tf(hBi(t)) 更新該蝙蝠的歷史最優(yōu)個(gè)體EndIfIf(rand1>ri) 利用式(9)將蝙蝠更新到某較好蝙蝠的附近EndIf隨機(jī)產(chǎn)生一個(gè)新蝙蝠(Xnew,Bnew) if(rand2f(Bnew)>f(P))P=Bnew,Y=Xnew; 用式(10)和(11)減小ai和增大ri

EndIf

EndFor

找到種群中歷史適應(yīng)度最好的蝙蝠，如果該歷史最優(yōu)個(gè)體好于全局最優(yōu)，則替代全局最優(yōu)個(gè)體(Y,P)

EndWhile

步驟5 輸出P和f(P)。

下面是算法中用到的公式。

Xnew=Xk(t) +εa；ε∈[0,1]是隨機(jī)數(shù)

(9)

ai=?ai

(10)

ri=ri[1-exp(-γt)]

(11)

式(9)中的a是所有蝙蝠響度ai的平均值；式(10)、(11)中00都是常數(shù)因子[5]，本文實(shí)驗(yàn)中?=γ=0.9。關(guān)于蝙蝠算法中各公式詳細(xì)介紹請(qǐng)參考文獻(xiàn)[5],限于篇幅不再贅述。

3 變異蝙蝠算法求解折扣背包問(wèn)題

3.1 編碼的處理

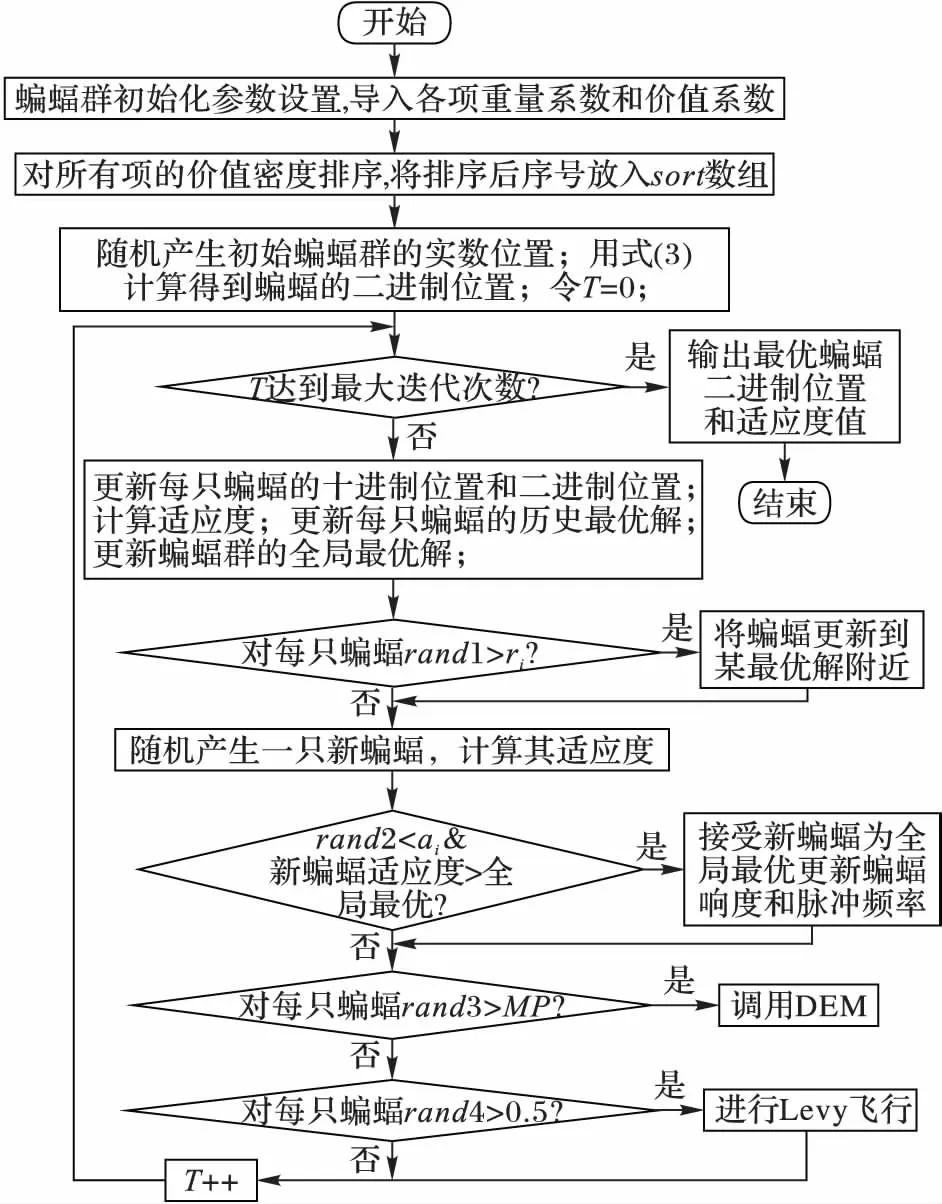
根據(jù)Guldan給出的數(shù)學(xué)模型，在利用雙重編碼的蝙蝠算法求解D{0-1}KP時(shí)，個(gè)體蝙蝠的十進(jìn)制編碼X=[x0,x1,x2,…,x3n-1]∈[0,1]3n，對(duì)應(yīng)的二進(jìn)制編碼為B=[b0,b1,b2,…,b3n-1] ∈{0,1}3n，當(dāng)bj=1(0≤j≤3n-1)時(shí)，表示項(xiàng)j被裝入背包，bj=0表示項(xiàng)j沒(méi)有被裝入。這種編碼方法雖然簡(jiǎn)單易行，但也存在一個(gè)明顯的缺點(diǎn)，就是不可行解會(huì)非常多[3]。本文將GROA[3]應(yīng)用到對(duì)蝙蝠個(gè)體適應(yīng)度值的計(jì)算中，消除不可行解并對(duì)可行解進(jìn)行優(yōu)化。設(shè)V={{v3i,v3i+1,v3i+2}|0≤i≤n-1}為D{0-1}KP的各項(xiàng)的價(jià)值集，W={{w3i,w3i+1,w3i+2}|0≤i≤n-1}為各項(xiàng)的重量集，C為背包載重。將3n個(gè)項(xiàng)根據(jù)價(jià)值密度vj/wj(0≤j≤3n-1)由大到小排序，并按照排序后的順序?qū)⒏黜?xiàng)的下標(biāo)存入數(shù)組sort[0…3n-1]中。設(shè)置數(shù)組flag[0…n-1]∈{0,1}n標(biāo)識(shí)各項(xiàng)集的狀態(tài)，flag[i]=0表示項(xiàng)集i中沒(méi)有項(xiàng)被裝入背包，flag[i]=1表示項(xiàng)集i中恰有一項(xiàng)被裝入背包，?i/3」表示對(duì)i/3向下取整。E=[e1,e2,…,e3n-1]∈{0,1}3n為修正優(yōu)化后的二進(jìn)制編碼，G=[g1,g2,…,g3n-1]∈[0,1]3n為其對(duì)應(yīng)的十進(jìn)制編碼。f(E)為修正優(yōu)化后蝙蝠個(gè)體的適應(yīng)度值。將GROA[3]應(yīng)用到計(jì)算蝙蝠個(gè)體的適應(yīng)度的函數(shù)GETFIT中，描述如下：

算法2 GETFIT。

輸入 原蝙蝠個(gè)體(X,B)和sort[0…3n-1]；

輸出 修正后的蝙蝠個(gè)體(G,E)及適應(yīng)度值f(E)。

weight=0,value=0For(j=0; j<3n-1; j++) ej=0

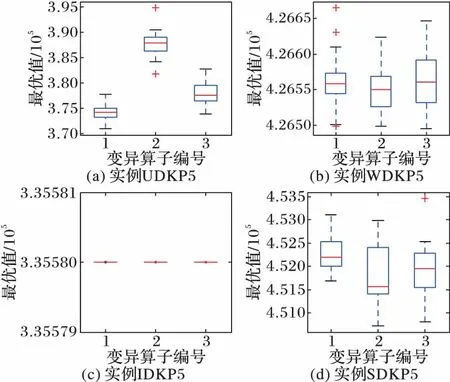
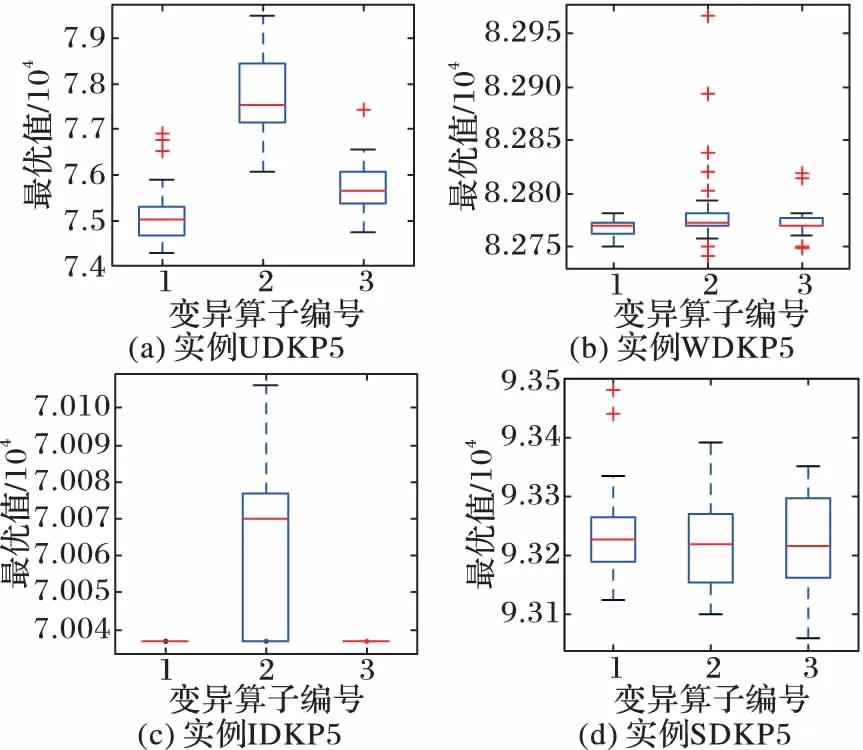
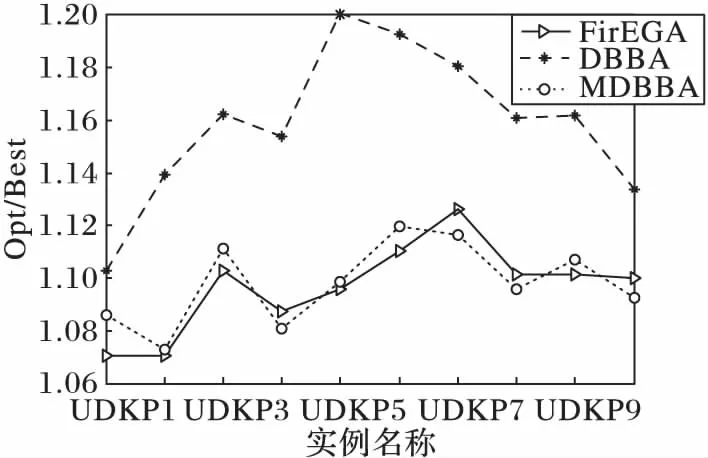
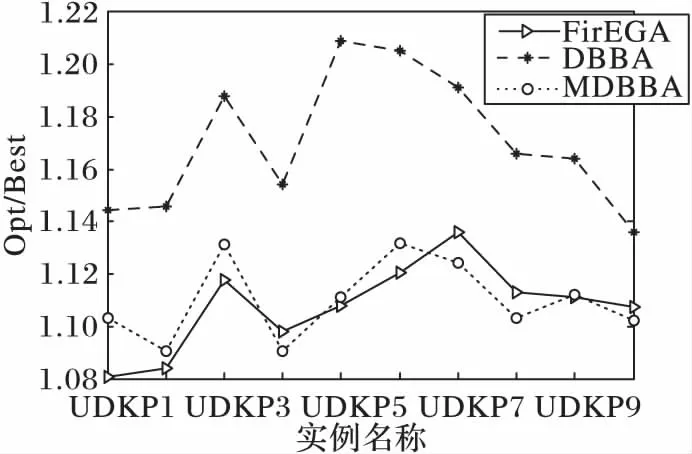
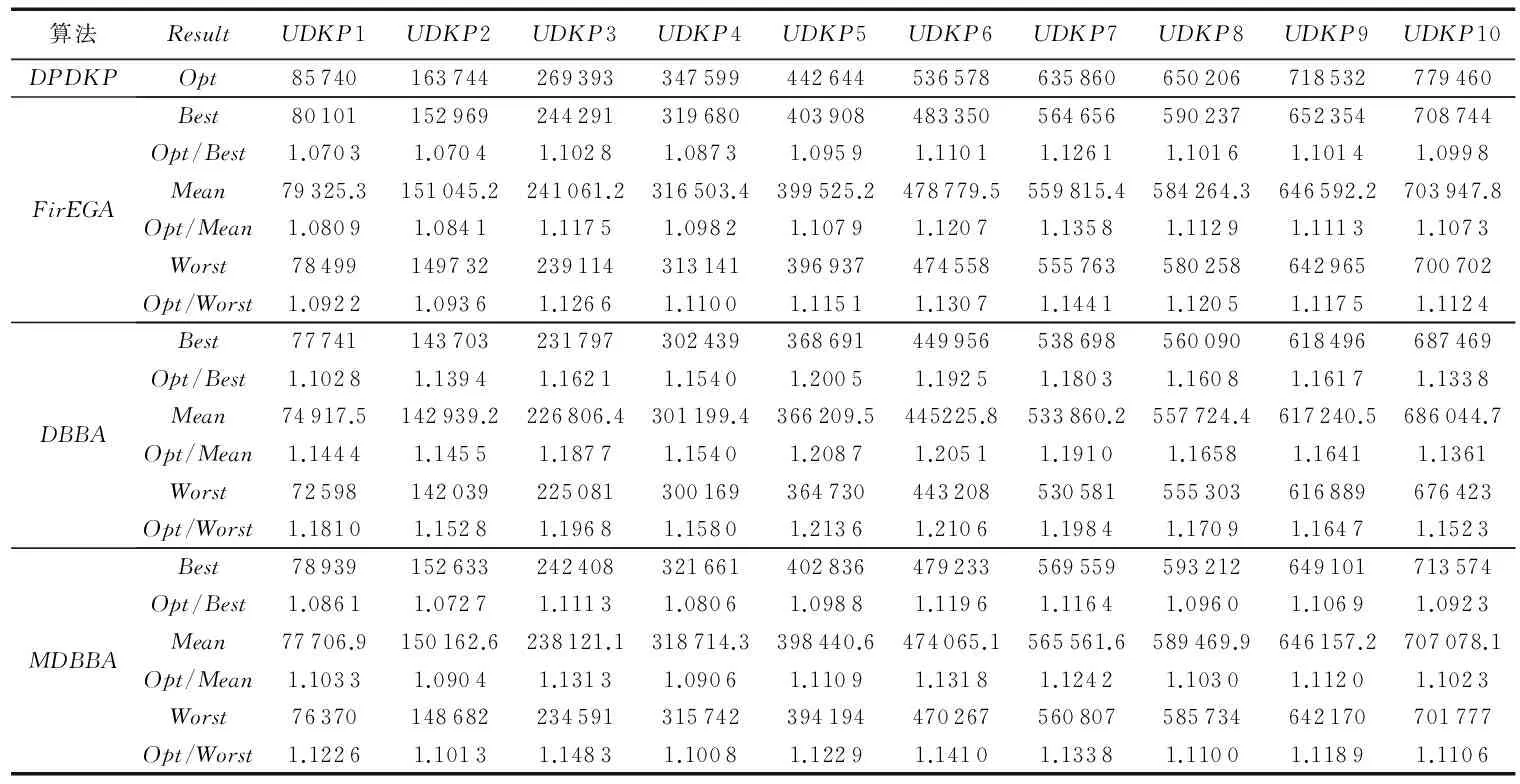
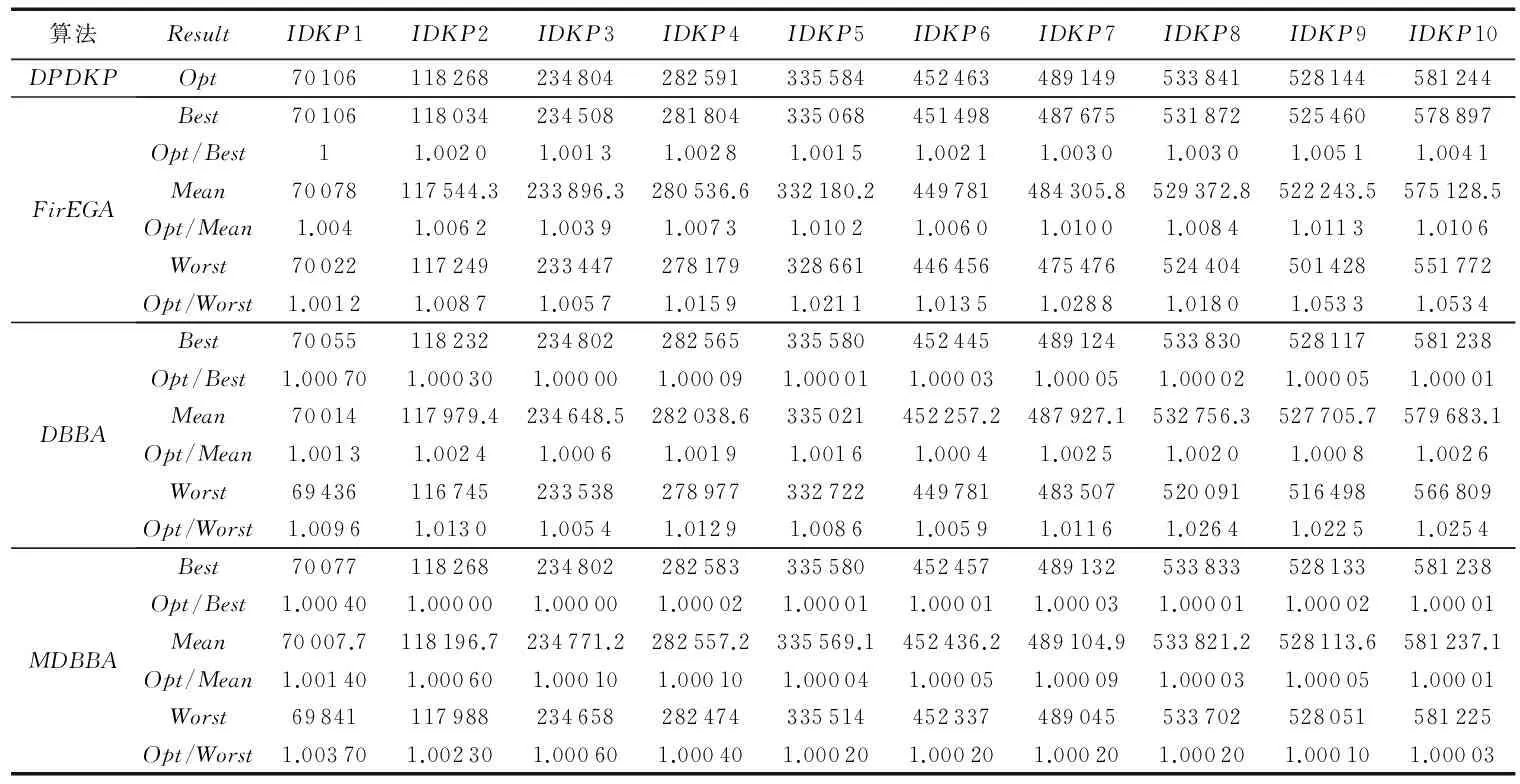
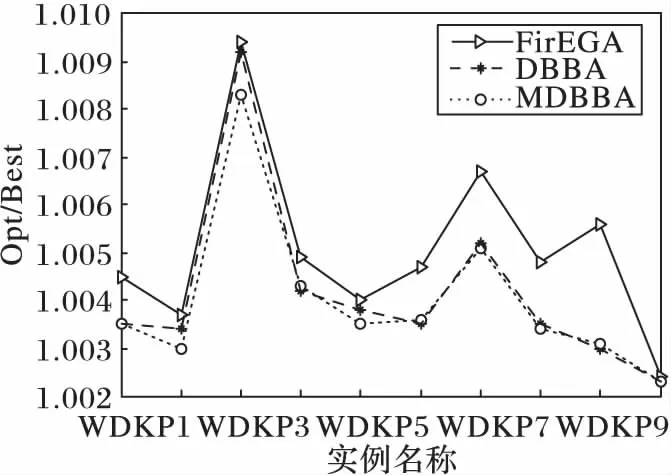
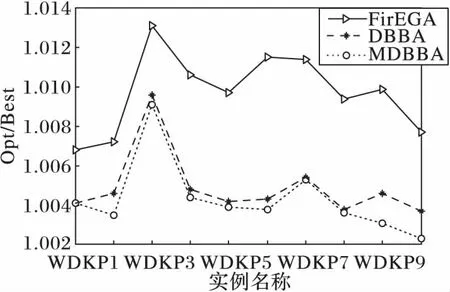
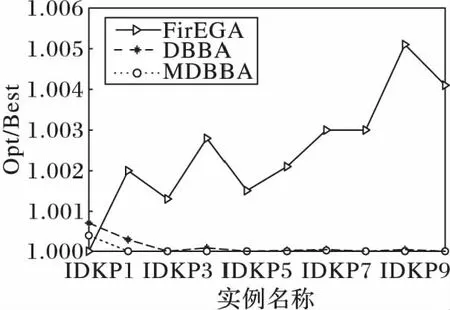
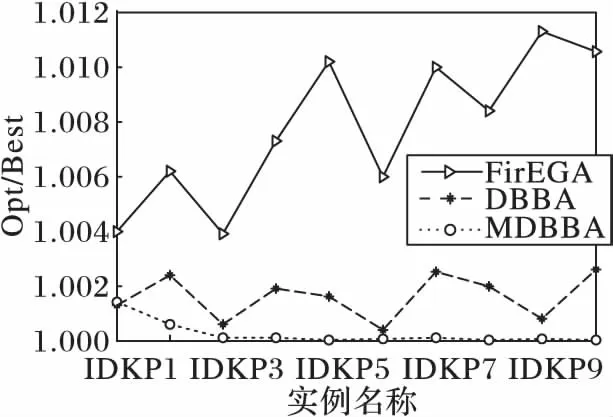
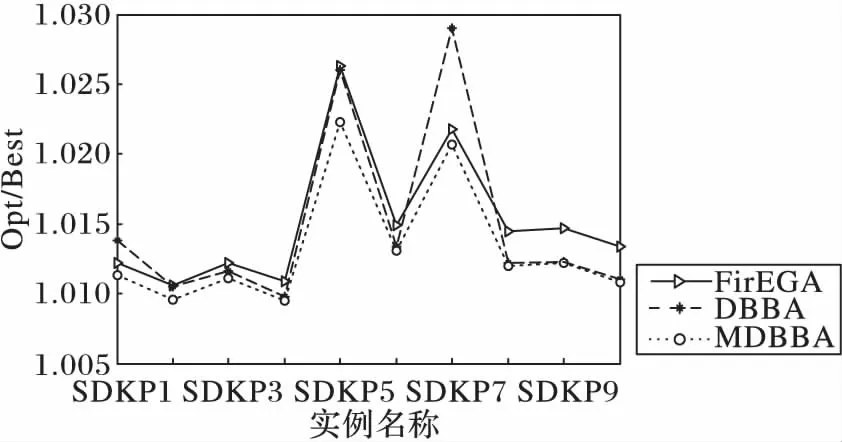
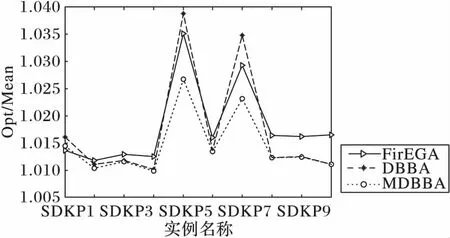
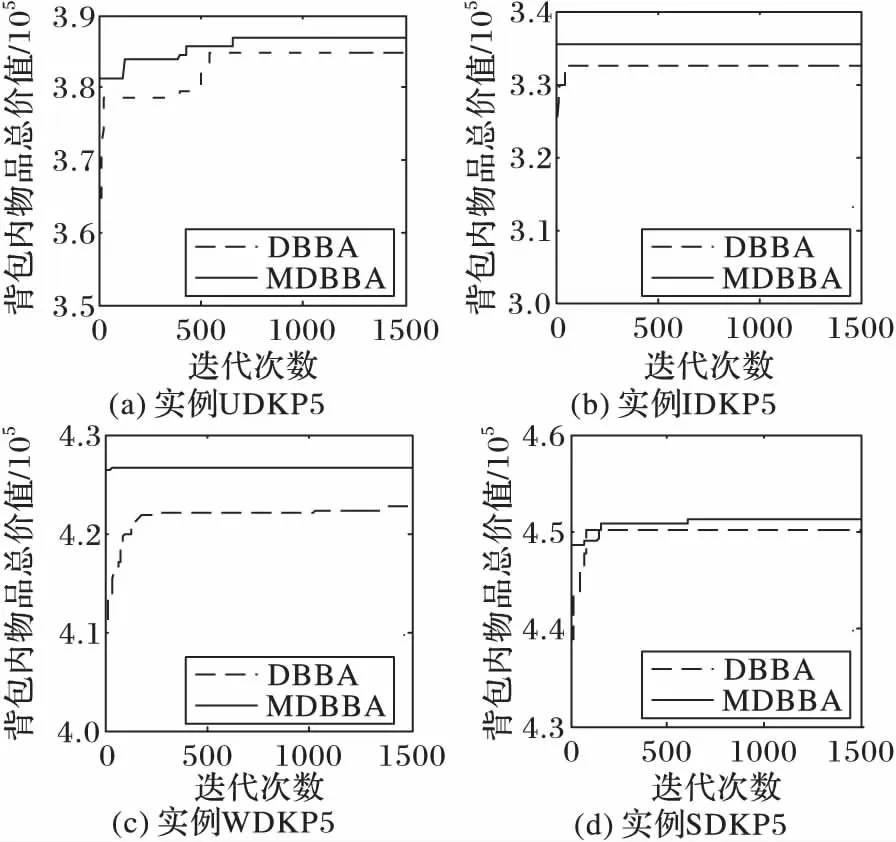
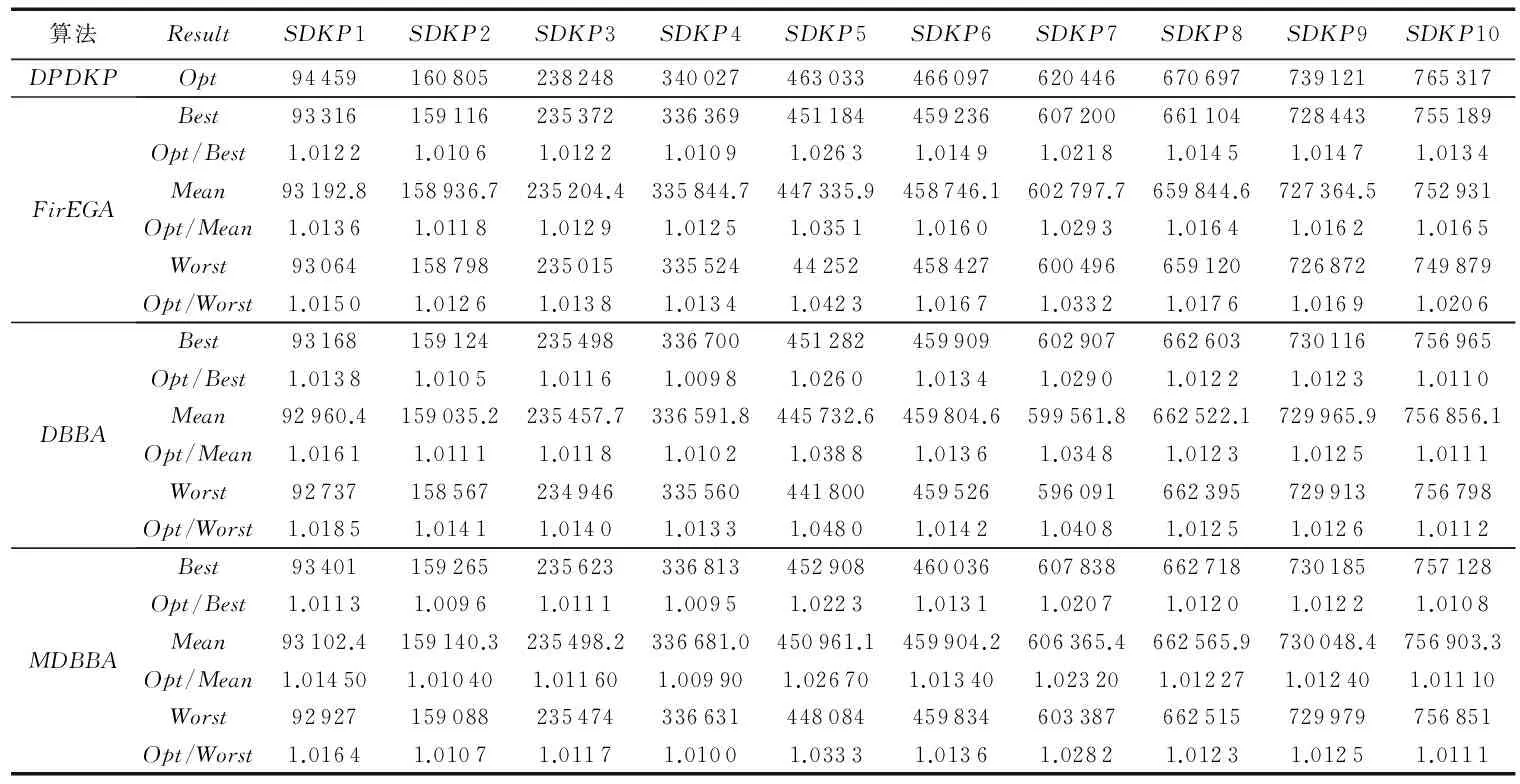
For(i=0; i

For(j=0; j<3n-1; j++)If(bsort[j]=1 & weight+wsort[j]≤C & flag[?sort[j]/3」]=0) esort[j]=1，gsort[j]=xsort[j]， value=value+vsort[j]weight=weight+wsort[j]，flag[?sort[j]/3」]=1

EndIf

EndFor

For(j=0; j<3n-1; j++)If((weight+wsort[j]≤C) & flag[?sort[j]/3」]=0)) esort[j]=1，gsort[j]=rand(), rand()∈[0,1]weight=weight+wsort[j]， flag[?sort[j]/3」]=1value=value+vsort[j]

EndIf

EndFor

f(E)=value

return(G,E, f(E))

將GETFIT算法應(yīng)用于算法DBBA求解適應(yīng)度值，即可求解D{0-1}KP，第4章對(duì)比實(shí)驗(yàn)中算法DBBA就是使用GETFIT后的DBBA。

3.2 基于差分的變異策略

差分演化的變異算子存在多種形式,其一般表示為DE/x/y/z[18]，x表示變異算子中差異向量進(jìn)行重組的基準(zhǔn)個(gè)體是隨機(jī)選取的還是當(dāng)前群體的最優(yōu)個(gè)體；y表示參與重組的差異向量個(gè)數(shù)；z表示重組所采用的方式，主要有指數(shù)重組方式和二項(xiàng)式重組方式，這里使用二項(xiàng)式重組。文獻(xiàn)[19]把二項(xiàng)式重組變異算子分為3類(lèi)：第1類(lèi)為DE/rand/1/bin和DE/rand/2/bin；第2類(lèi)為DE/best/1/bin和DE/best/2/bin；第3類(lèi)是DE/rand-to-best/1/bin模式。為了提高蝙蝠算法種群的多樣性，本文從每類(lèi)模式中選擇一種分別應(yīng)用于蝙蝠算法中，測(cè)試其有效性。測(cè)試數(shù)據(jù)將在第4章給出。變異策略用算法DEM(DifferentEvolutionMutation)實(shí)現(xiàn)：

算法3DEM。

輸入 原蝙蝠個(gè)體，原適應(yīng)度值；

輸出 經(jīng)過(guò)變異策略后的蝙蝠個(gè)體，新適應(yīng)度值。

1)應(yīng)用差分變異算子產(chǎn)生子蝙蝠個(gè)體十進(jìn)制位置；

2)根據(jù)式(3)計(jì)算子蝙蝠的二進(jìn)制位置；

3)用GETFIT得到子蝙蝠的適應(yīng)值；

4)如果子蝙蝠的適應(yīng)度好于原蝙蝠；

5)用子蝙蝠替換原蝙蝠。

變異操作使得蝙蝠個(gè)體之間可以相互交流，增加了蝙蝠群體探索和尋優(yōu)能力，另外精英個(gè)體保留機(jī)制提高了算法的收斂速度。

3.3Lévy飛行

啟發(fā)式算法在尋優(yōu)過(guò)程中往往容易陷入局部極值，這里通過(guò)蝙蝠個(gè)體的Lévy飛行來(lái)降低算法陷入局部極值的可能性。Lévy飛行是一種隨機(jī)游走過(guò)程，它的步長(zhǎng)是一種連續(xù)的重尾分布[20]。從數(shù)學(xué)角度看，Lévy飛行行為體現(xiàn)出的是一類(lèi)非高斯隨機(jī)過(guò)程，其平穩(wěn)增量服從Lévy穩(wěn)定分布，Lévy飛行過(guò)程中會(huì)發(fā)生大的跳躍且方向多變，其典型軌跡表現(xiàn)為由較小跳躍組成的聚集被較大的跳躍分隔開(kāi)的現(xiàn)象，可以借助大的跳躍逃離局部極值[21]。為了避免算法過(guò)早地陷入局部極值中，在算法中，每次迭代后個(gè)體蝙蝠按照一定概率(本文定為0.5)進(jìn)行Lévy飛行，按式(12)產(chǎn)生飛行后的十進(jìn)制位置[20]：

Xi′=Xi+a⊕Lévy(λ)

(12)

其中：Xi為原蝙蝠實(shí)數(shù)位置，Xi′為飛行后的實(shí)數(shù)位置,其中Lévy(λ)來(lái)自于Lévy分布[20]。用式(5)確定其二進(jìn)制位置后通過(guò)GETFIT算法計(jì)算飛行后的適應(yīng)度值，如果適應(yīng)度優(yōu)于原蝙蝠則用新位置替代原蝙蝠的位置。

3.4 變異蝙蝠算法求解折扣背包問(wèn)題流程

用算法MDBBA求解D{0-1}問(wèn)題的蝙蝠算法流程如圖1所示。每只蝙蝠的適應(yīng)度均由算法GETFIT求得；用式(6)～(8)、(5)更新蝙蝠的速度Vi(t)和實(shí)數(shù)位置Xi(t)和二進(jìn)制位置Bi(t)。MP是蝙蝠進(jìn)行變異操作的概率，本文設(shè)為0.8；rand1，rand2，rand3，rand4均為在[0,1]上產(chǎn)生的隨機(jī)數(shù)。

4 仿真實(shí)驗(yàn)結(jié)果分析

使用文獻(xiàn)[3]給出的4類(lèi)D{0-1}KP實(shí)例：不相關(guān)D{0-1}KP實(shí)例(Uncorrelated instances of D{0-1}KP，UDKP)、弱相關(guān)D{0-1}KP 實(shí)例(Weakly correlated instances of D{0-1}KP，WDKP)、強(qiáng)相關(guān)D{0-1}KP 實(shí)例(Strongly correlated instances of D{0-1}KP, SDKP)和逆向強(qiáng)相關(guān)D{0-1}KP實(shí)例(Inverse strongly correlated instances of D{0-1}KP，IDKP)，其中每類(lèi)有10 個(gè)不同規(guī)模的實(shí)例。關(guān)于實(shí)例詳細(xì)介紹請(qǐng)參考文獻(xiàn)[3]。本文針對(duì)4類(lèi)D{0-1}KP實(shí)例進(jìn)行了兩組實(shí)驗(yàn)：實(shí)驗(yàn)1是將三種差分的變異算子分別與蝙蝠算法結(jié)合，通過(guò)對(duì)實(shí)例運(yùn)行結(jié)果的箱圖(BOXPLOT)分析確定使用的變異算子; 實(shí)驗(yàn)2是通過(guò)四類(lèi)大規(guī)模D{0-1}KP 實(shí)例的各種計(jì)算結(jié)果,對(duì)MDBBA與DBBA和文獻(xiàn)[3]的FirEGA算法進(jìn)行比較。仿真計(jì)算所使用微機(jī)的硬件環(huán)境為，操作系統(tǒng)Windows 10，編程環(huán)境VC++2010。MDBBA與DBBA各個(gè)參數(shù)的設(shè)置：Xmax=1.0；Xmin=-1.0；Vmax=1.0；fmin=0.01；fmax=0.071；蝙蝠個(gè)體初始脈沖頻率r0=0.05；初始化脈沖響度a0=1.0；脈沖音強(qiáng)衰減系數(shù)和脈沖頻率增強(qiáng)系數(shù)=0.9；變異概率MP=0.8，Lévy飛行概率為0.5；種群規(guī)模是40；迭代次數(shù)均等于實(shí)例的規(guī)模(即3n)。FirEGA算法數(shù)據(jù)來(lái)自文獻(xiàn)[3]。

圖1 變異蝙蝠算法求解折扣背包算法流程Fig. 1 Flowchart of mutated bat algorithm for solving D{0-1}KP

4.1 變異算子性能比較

這里將DE/rand/1/bin、DE/best/1/bin、DE/rand-to-best/1/bin(編號(hào)為1、2、3)三種變異算子分別應(yīng)用于蝙蝠算法中，測(cè)試其有效性。抽取維數(shù)為100和500的8組實(shí)例進(jìn)行測(cè)試。圖2、3是30次獨(dú)立運(yùn)行各組合形式得到的最優(yōu)值的統(tǒng)計(jì)結(jié)果形成的箱圖。根據(jù)八個(gè)箱圖比較,第2類(lèi)模式的變異算子(編號(hào)2)使得算法有較高的穩(wěn)定性，產(chǎn)生的最優(yōu)值也基本都高于另外兩類(lèi)模式，所以本文確定使用DE/best/1/bin作為變異算子。實(shí)驗(yàn)2中算法MDBBA變異部分使用該變異算子。

4.2 MDBBA、DBBA與FirEGA的實(shí)驗(yàn)結(jié)果比較

利用FirEGA、DBBA與MDBBA求解四類(lèi)D{0-1}KP 實(shí)例的計(jì)算結(jié)果見(jiàn)表1～4，其中Opt為由動(dòng)態(tài)規(guī)劃法(記為DPDKP)計(jì)算出的實(shí)例最優(yōu)值；Best、Worst 和Mean 分別為FirEGA，DBBA與MDBBA在30次獨(dú)立計(jì)算中得到的所有結(jié)果的最好值、最差值以及所有結(jié)果的數(shù)學(xué)期望；Opt/Best、Opt/Worst 和Opt/Mean 分別表示以上各值的近似比[22-23]。

為更直觀地比較實(shí)驗(yàn)結(jié)果，將FirEGA、DBBA與MDBBA求解四類(lèi)D{0-1}KP 實(shí)例的最好值近似比和平均值近似比以曲線圖的形式展現(xiàn)出來(lái)，如圖4～11。

圖2 三種不同算子在100維四類(lèi)實(shí)例下的比較Fig. 2 Comparison of 3 different operators in 4 types of 100 dimensions

圖3 三種不同算子在500維四類(lèi)實(shí)例下的比較Fig. 3 Comparison of 3 different operators in 4 types of 500 dimensions

圖4 UDKP類(lèi)實(shí)例最好值的近似比Fig. 4 Approximate ratio of the best value of UDKP

圖5 UDKP類(lèi)實(shí)例平均值的近似比Fig.5 Approximate ratio of the average of UDKP

從表1中可以看出：FirEGA求解UDKP實(shí)例所得最好值的近似比基本在1.10左右，平均值和最差值的近似比均不超過(guò)1.144 1；DBBA所得最好值的近似比在1.16 左右，平均值和最差值的近似比都在1.213 6以下；MDBBA求解UDKP實(shí)例所得最好值的近似比在1.09左右，平均值和最差值的近似比均不超過(guò)1.148 3。圖4是三種算法求解UDKP1～UDKP10

實(shí)例的最好值的近似比比較，圖5是三種算法求解UDKP1～UDKP10實(shí)例平均值的近似比比較圖。從兩圖中可以看出，DBBA求解能力最差，經(jīng)過(guò)加入變異和Lévy飛行后的MDBBA求解能力有很大的提高，最好值近似比和平均值近似比基本和FirEGA相當(dāng)，有4個(gè)實(shí)例超出FirEGA。

表1 對(duì)實(shí)例UDKP1～UDKP10的實(shí)驗(yàn)結(jié)果比較Tab. 1 Comparison of experimental results of examples UDKP1 ～ UDKP10

表2 對(duì)實(shí)例WDKP1～WDKP10的實(shí)驗(yàn)結(jié)果對(duì)比Tab. 2 Comparison of Experimental Results of Examples WDKP1 ～ WDKP10

從表2中可以看出FirEGA求解WDKP實(shí)例所得到的最好值的近似比不超過(guò)1.009 4，平均值的近似比不超過(guò)1.013 1，最差值的近似比不超過(guò)1.028 2；DBBA求解WDKP實(shí)例所得到的最好值的近似比不超過(guò)1.009 2，平均值的近似比不超過(guò)1.009 6，最差值的近似比不超過(guò)1.034 0；MDBBA求解WDKP實(shí)例所得到的最好值的近似比不超過(guò)1.008 3，平均值的近似比不超過(guò)1.009 1，最差值的近似比不超過(guò)1.009 2。圖6是三種算法求解WDKP1～WDKP10實(shí)例的最好值的近似比比較，圖7是平均值的近似比比較。DBBA在求解WDKP實(shí)例中求得最優(yōu)值近似比，平均值近似比都好于FirEGA；而MDBBA的最好值近似比、平均值近似比在每個(gè)實(shí)例上都優(yōu)與DBBA。

表3 對(duì)實(shí)例IDKP1～I(xiàn)DKP10的實(shí)驗(yàn)結(jié)果對(duì)比Tab. 3 Comparison of Experimental Results of Examples IDKP1 ～ IDKP10

圖6 WDKP類(lèi)實(shí)例最好值的近似比Fig. 6 Approximate ratio of the best value of WDKP

圖7 WDKP類(lèi)實(shí)例平均值的近似比Fig. 7 Approximate ratio of the average of WDKP

圖8 IDKP類(lèi)實(shí)例最好值的近似比Fig. 8 Approximate ratio of the best value of IDKP

從表3中可以看出：FirEGA求解IDKP實(shí)例所得最好值的近似比不超過(guò)1.005 1，平均值的近似比不超過(guò)1.011 3，最差值的近似比不超過(guò)1.053 4；DBBA求解IDKP 實(shí)例所得到的最好值的近似比不超過(guò)1.000 7，平均值的近似比不超過(guò)1.002 5，最差值的近似比不超過(guò)1.026 4；MDBBA求解IDKP 實(shí)例所得到的最好值的近似比不超過(guò)1.000 4，平均值的近似比不超過(guò)1.001 4，最差值的近似比不超過(guò)1.003 7。圖8是三種算法求解IDKP1～I(xiàn)DKP10實(shí)例的最好值的近似比，圖9是平均值的近似比。從兩圖中明顯看出DBBA和MDBBA求解效果明顯優(yōu)于FirEGA；DBBA和MDBBA比較，MDBBA求解效果和平均求解能力都更好。

圖9 IDKP類(lèi)實(shí)例平均值的近似比Fig. 9 Approximate ratio of the average of IDKP

圖10 SDKP類(lèi)實(shí)例最好值的近似比Fig. 10 Approximate ratio of the best value of SDKP

從表4中可以看出：FirEGA求解SDKP 實(shí)例所得到的最好值的近似比均不超過(guò)1.026 3，平均值的近似比不超過(guò)1.035 1，最差值的近似比也均不超過(guò)1.042 3；DBBA求解SDKP 實(shí)例所得到的最好值的近似比不超過(guò)1.026 0，平均值的近似比不超過(guò)1.038 8，最差值的近似比不超過(guò)1.048 0；MDBBA求解SDKP 實(shí)例所得到的最好值的近似比不超過(guò)1.022 3，平均值的近似比不超過(guò)1.026 7，最差值的近似比不超過(guò)1.033 3。圖10是三種算法求解SDKP1～SDKP10實(shí)例的最好值的近似比比較，圖11是平均值的近似比比較圖，從兩圖中看出：雙重編碼蝙蝠算法DBBA求解SDKP實(shí)例能力比FirEGA略弱，MDBBA在求解能力上優(yōu)于FirEGA。

圖11 SDKP類(lèi)實(shí)例平均值的近似比Fig. 11 Approximate ratio of the average of SDKP

為了進(jìn)一步比較雙重編碼蝙蝠算法DBBA和變異雙重編碼蝙蝠算法MDBBA的平均求解性能，圖12給出它們30 次獨(dú)立運(yùn)行實(shí)例UDKP5、WDKP5、SDKP5和IDKP5 的平均收斂曲線。由圖可以看出：MDBBA的平均收斂速度非常快，基本上在不超過(guò)0.2*MaxIt 的迭代次數(shù)內(nèi)即可獲得極好的結(jié)果；DBBA的平均收斂速度相對(duì)慢，并且它的平均求解結(jié)果也明顯比MDBBA的差。

圖12 對(duì)DBBA和MDBBA平均收斂曲線比較Fig. 12 Comparison of average convergence curve of DBBA and MDBBA

基于對(duì)四類(lèi)D{0-1}KP實(shí)例的計(jì)算、比較和分析可以知，對(duì)于項(xiàng)的價(jià)值系數(shù)和重量系數(shù)均在大范圍內(nèi)隨機(jī)取值的D{0-1}KP實(shí)例，MDBBA均能夠求得一個(gè)近似比接近于1 的近似解，是求解大規(guī)模難D{0-1}KP實(shí)例的有效且實(shí)用的進(jìn)化算法。從算法求得的最好結(jié)果來(lái)看，DBBA、MDBBA和FirEGA的求解能力基本相當(dāng)，DBBA在求解UDKP實(shí)例中效果明顯不如MDBBA和FirEGA；從算法的平均求解性能來(lái)看，MDBBA的求解效果優(yōu)于FirEGA和DBBA。

表4 對(duì)實(shí)例SDKP1～SDKP10的實(shí)驗(yàn)結(jié)果對(duì)比Tab. 4 Comparison of experimental results of examples SDKP1 ～ SDKP10

5 結(jié)語(yǔ)

本文研究了如何利用變異蝙蝠算法求解D{0-1}KP，提出利用雙重編碼方式求解D{0-1}KP，將貪心和優(yōu)化策略應(yīng)用于個(gè)體適應(yīng)度求解中；針對(duì)蝙蝠算法易早熟、求解精度不高的缺陷，在蝙蝠群更新位置后利用差分變異增加種群多樣性，提高全局搜索能力；通過(guò)蝙蝠個(gè)體的Lévy飛行避免群體過(guò)早的陷入局部極值。對(duì)四類(lèi)大規(guī)模D{0-1}KP實(shí)例的計(jì)算結(jié)果比較與分析，MDBBA不受實(shí)例中各項(xiàng)的價(jià)值系數(shù)、重量系數(shù)和背包載重的大小影響，對(duì)于大規(guī)模的難D{0-1}KP實(shí)例，能夠快速求得一個(gè)近似比接近于1的近似解。比基本雙重編碼的蝙蝠算法無(wú)論在收斂速度還是在尋優(yōu)能力上都有極大提高，是求解大規(guī)模難D{0-1}KP實(shí)例的實(shí)用進(jìn)化算法。

)

[1]GULDANB.Heuristicandexactalgorithmsfordiscountedknapsackproblems[D].Nuremberg:UniversityofErlangen-Nuremberg, 2007.

[2]RONGA,FIGUEIRAJR,KLAMROTHK.Dynamicprogrammingbasedalgorithmsforthediscounted{0-1}knapsackproblem[J].AppliedMathematicsandComputation, 2012, 218(12): 6921-6933.

[3] 賀毅朝, 王熙照，李文斌, 等. 基于遺傳算法求解折扣{0-1}背包問(wèn)題的研究[J].計(jì)算機(jī)學(xué)報(bào),2016,39(12):2614-2630.(HEYC,WANGXZ,LIWB,etal.Researchongeneticalgorithmsforthediscounted{0-1}knapsackproblem[J].ChineseJournalofComputers, 2016,39(12):2614-2630.)

[4]HEY,WANGX,HEY,etal.Exactandapproximatealgorithmsfordiscounted{0-1}knapsackproblem[J].InformationSciences, 2016, 369(10): 634-647.

[5]YANGX.Anewmetaheuristicbat-inspiredalgorithm[C]//NICSO2010:NatureInspiredCooperativeStrategiesforOptimization.Berlin:Springer, 2010, 284: 65-74.

[6] 吳聰聰，賀毅朝，陳嶷瑛,等. 求解0-1背包問(wèn)題的二進(jìn)制蝙蝠算法[J].計(jì)算機(jī)工程與應(yīng)用, 2015, 51(19):71-74.(WUCC,HEYC,CHENYY,etal.Binarybatalgorithmforsolving0-1knapsackproblem[J].ComputerEngineeringandApplications, 2015,51(19):71-74.)

[7] 賀興時(shí)，丁文靜，楊新社.基于模擬退火高斯擾動(dòng)的蝙蝠優(yōu)化算法[J],計(jì)算機(jī)應(yīng)用研究,2013, 31(2)：392-397.(HEXS,DINGWJ,YANGXS.BatalgorithmbasedonsimulatedannealingandGaussianperturbations[J].ApplicationResearchofComputers, 2013, 31(2):392-397.)

[8] 謝健，周永權(quán)，陳歡.一種基于Lévy飛行軌跡的蝙蝠算法[J].模擬識(shí)別與人工智能,2013,26(9): 829-837.(XIEJ,ZHOUYQ,CHENH.AbatalgorithmbasedonLévyflightstrajectory[J].PatternRecognitionandArtificialIntelligence, 2013,26(9)：829-837.)

[9] 劉長(zhǎng)平，葉春明.具有混沌搜索策略的蝙蝠優(yōu)化算法及性能仿真[J].系統(tǒng)仿真學(xué)報(bào),2013,25(6): 1183-1188.(LIUCP,YECM.Batalgorithmwithchaoticsearchstrategyandanalysisofitsproperty[J].JournalofSystemSimulation,2013,25(6): 1183-1188.)

[10]YANGX.Batalgorithmformultiobjectiveoptimization[J].InternationalJournalofBio-InspiredComputation, 2011, 3(5):267-274.

[11]YANGX,GANDOMIAH.Batalgorithm:anovelapproachforglobalengineeringoptimization[J]．EngineeringComputations，2012, 29(5): 464-483.

[12]LEMMATA,BINMHF.Useoffuzzysystemsandbatalgorithmforenergymodelinginagasturbinegenerator[C]//Proceedingsofthe2011IEEEColloquiumonHumanities,ScienceandEngineering.Piscataway,NJ:IEEE, 2011: 305-310.

[13] 盛曉華，葉春明.基于蝙蝠算法的PFSP調(diào)度干擾管理研究[J]. 計(jì)算機(jī)工程與應(yīng)用, 2014,50(8):241-246. (SHENGXH,YECM.ResearchofbatalgorithmfordisruptionmanagementonPFSPscheduling[J].ComputerEngineeringandApplications, 2014,50(8): 241-246.)

[14]MISHRAS,SHAWK,MISHRAD.Anewmeta-heuristicbatinspiredclassificationapproachformicroarraydata[J].ProcediaTechnology, 2012, 4(1): 802-806.

[15]KHANK,SAHAIA.AcomparisonofBA，GA，PSO，BPandLMfortrainingfeedforwardneuralnetworksine-learningcontext[J]．InternationalJournalofIntelligentSystemsandApplications，2012,4(7) : 23-29.

[16]KHANK，NIKOVA，SAHAIA.Afuzzybatclusteringmethodforergonomicscreeningofofficeworkplaces[C]//Proceedingsofthe3rdInternationalConferenceonSoftware,ServicesandSemanticTechnologies.Berlin:Springer, 2011: 59-66.

[17] 賀毅朝，王彥祺，劉建芹．一種適于求解離散問(wèn)題的二進(jìn)制粒子群優(yōu)化算法[J]．計(jì)算機(jī)應(yīng)用與軟件, 2007,24(1):157-159.(HEYC,WANGYQ,LIUJQ.Anewbinaryparticleswarmoptimizationforsolvingdiscreteproblems[J].ComputerApplicationsandSoftware, 2007,24(1):157-159.)

[18]NOMANN,IBAH.Enhancingdifferentialevolutionperformancewithlocalsearchforhighdimensionalfunctionoptimization[C]//Proceedingsofthe7thAnnualConferenceonGeneticandEvolutionaryComputation.NewYork:ACM, 2005: 967-974.

[19] 賀毅朝,王熙照, 劉坤起,等.差分演化的收斂性分析與算法改進(jìn)[J]. 軟件學(xué)報(bào),2010,21(5): 875-885.(HEYC,WANGXZ,LIUKQ,etal.Convergentanalysisandalgorithmicimprovementofdifferentialevolution[J].JournalofSoftware, 2010, 21(5): 875-885.)

[20]YANGX,DEBS.CuckoosearchviaLévyflights[C]//ProceedingsofWorldCongressonNature&BiologicallyInspiredComputing.Piscataway,NJ:IEEE, 2009: 210-214.

[21] 劉長(zhǎng)平，葉春明.具有Lévy飛行特征的蝙蝠算法[J].智能系統(tǒng)學(xué)報(bào)，2013,8(3):240-246.(LIUCP,YECM.BatalgorithmwiththecharacteristicsofLévyflights[J].CAAITransactionsonIntelligentSystems,2013,8(3):240-246.)

[22]CORMENTH,LEISERSONCE,RIVESTRL,etal.IntroductiontoAlgorithms[M]. 3rded.Cambridge:MITPress, 2001:1117-1119.

[23]ALSUWAIYELMH.AlgorithmsDesignTechniquesandAnalysis[M].Singapore:WorldScientificPublishingCompany, 1999:410-418.

ThisworkispartiallysupportedbyScientificResearchProjectProgramofCollegesandUniversitiesinHebeiProvince(ZD2016005),theNaturalScienceFoundationofHebeiProvince(F2016403055).

WU Congcong, born in 1975, M. S., lecturer. Her research interests include intelligent computing, information retrieval, machine learning.

HE Yichao,born in 1969, M. S., professor. His interests include the theory and applications of evolutionary algorithm, design and analysis of algorithms,computational complexity theory and group testing theory.

CHEN Yiying,born in 1971, Ph.D., professor. Her research interests include machine learning, geographic information system.

LIU Xuejing,born in 1980, M. S., lecturer. Her research interests include intelligent computing, machine learning.

CAI Xiufeng,born in 1979, M. S., lecturer. Her research interests include intelligent computing, machine learning.

Mutated bat algorithm for solving discounted {0-1} knapsack problem

WU Congcong*, HE Yichao,CHEN Yiying, LIU Xuejing,CAI Xiufeng

(CollegeofInformationEngineering,HebeiGEOUniversity,ShijiazhuangHebei050031,China)

Since the deterministic algorithms are difficult to solve the Discounted {0-1} Knapsack Problem (D{0-1}KP) with large-scale and wide data range, a Mutated Double codes Binary Bat Algorithm (MDBBA) was proposed. Firstly, the coding problem of D{0-1} KP was solved by double coding. Secondly, the Greedy Repair and Optimization Algorithm (GROA) was applied to the individual fitness calculation of bats, and the algorithm was quickly and effectively solved. Then, the mutation strategy in Differential Evolution (DE) was selected to improve the global optimization ability. Finally, Lévy flight was carried out by the bat individual according to certain probability to enhance the ability of the algorithm to explore and jump out of local extrema. Simulation was tested on four large-scale instances. The result shows that MDBBA is very suitable for solving large-scale D {0-1} KP, which has better optimal value and mean value than FirEGA (First Genetic Algorithm) algorithm and Double Binary Bat Algorithm (DBBA), and MDBBA converges significantly faster than DBBA.

Discounted {0-1} Knapsack Problem (D{0-1}KP); Bat Algorithm (BA); differential evolution; Lévy flight; greedy strategy; non-normal coding

2016-10-24;

2016-12-08。

河北省高等學(xué)校科學(xué)研究計(jì)劃項(xiàng)目(ZD2016005);河北省自然科學(xué)基金資助項(xiàng)目(F2016403055)。

吳聰聰(1975—)，女，河北唐山人，講師，碩士，主要研究方向：智能計(jì)算、信息檢索、機(jī)器學(xué)習(xí)； 賀毅朝(1969—)，男，河北晉州人，教授， CCF高級(jí)會(huì)員，主要研究方向：進(jìn)化算法理論與應(yīng)用、算法設(shè)計(jì)與分析、計(jì)算復(fù)雜性理論與群測(cè)試?yán)碚摚?陳嶷瑛(1971—)，女，湖南寧遠(yuǎn)人，教授，博士，主要研究方向:機(jī)器學(xué)習(xí)、地理信息系統(tǒng)； 劉雪靜(1980—)，女，河北定州人，講師，碩士，主要研究方向:智能計(jì)算、機(jī)器學(xué)習(xí)；才秀鳳(1979—)，女，河北豐潤(rùn)人，講師，碩士，主要研究方向:智能計(jì)算、機(jī)器學(xué)習(xí)。

1001-9081(2017)05-1292-08

10.11772/j.issn.1001-9081.2017.05.1292

TP18

A