基于短時傅里葉變換的噪聲移頻類靈巧干擾特征提取
宮 健,張 磊,陳 晨,熊 武
(1.西安電子科技大學,陜西 西安 710071;2.空軍工程大學,陜西 西安 710051;3.解放軍66133部隊,北京 100043;4.解放軍93792部隊,河北 廊坊 065000;5.解放軍94907部隊,江西 南昌 330013)
?
基于短時傅里葉變換的噪聲移頻類靈巧干擾特征提取
宮 健1,2,張 磊3,陳 晨4,熊 武5
(1.西安電子科技大學,陜西 西安 710071;2.空軍工程大學,陜西 西安 710051;3.解放軍66133部隊,北京 100043;4.解放軍93792部隊,河北 廊坊 065000;5.解放軍94907部隊,江西 南昌 330013)
靈巧干擾兼備壓制干擾和欺騙干擾的特點,其主要的技術指標為干擾的瞬時變化性和隨機生成性,傅里葉變換作為常用的信號處理工具只適用于確定信號和平穩信號,并不能對靈巧干擾進行有效分析,針對這一問題采用短時傅里葉變換來提取出噪聲移頻類靈巧干擾的特征,仿真了信號參數對干擾效果的影響,得出了有利于新型綜合電子干擾系統研制和對抗的一些結論。
靈巧干擾;時頻分析;噪聲移頻;短時傅里葉變換
0 引 言
雷達系統的電子干擾與反干擾技術在高技術軍事戰爭中發揮著越來越重要的作用,各種新技術也隨之迅猛發展[1-3]。靈巧干擾正是在各種先進的雷達技術普遍應用、傳統的壓制性干擾和欺騙性干擾不再能有效發揮作用的背景下提出的。
靈巧干擾作為一種新型干擾,兼備壓制性和欺騙性雙重優勢,通常是用在雷達工作頻率范圍發射多個在時間上與真實回波信號重疊,并且遮蓋住回波噪聲的猝發式脈沖的方式實現[4-6]。
靈巧干擾的主要技術指標為干擾信號的瞬時變化性和隨機生成性,傅里葉變換作為常用的信號處理工具,只適用于確定信號和平穩信號,并不能對靈巧干擾進行有效分析,因此本文研究了時頻分析的基本工具——短時傅里葉變換來提取出噪聲移頻類靈巧干擾特征的方法。
1 雷達回波匹配濾波處理模型
1.1 線性調頻信號
假設脈沖壓縮雷達發射的波形為線性調頻信號,表示為:
(1)
式中:T為脈沖寬度;μ=B/T為調頻斜率;B為調頻帶寬。
對應匹配濾波器的頻率響應為:
H(f)=kS*(f)exp(-j2πft0)
(2)
式中:k為匹配濾波器增益;t0為匹配濾波器的固有物理延遲。
為了數學分析的方便,可假設t0=0。濾波器的相頻特性與回波信號的相頻特性相反,即:
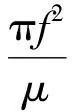
(3)
線性調頻信號經匹配濾波器輸出頻譜為:

(4)
1.2 二相編碼信號
二相編碼脈沖信號的復數表達式為:
s(t)=u(t)exp(j2πf0t)
(5)
(6)
式中:u(t)為回波復包絡;τ為子脈沖的時長;N為子脈沖的個數;T為整個編碼的脈沖時長;φ(t)∈{φn=0,π},表示采用的相位調制函數;f0為工作頻率。
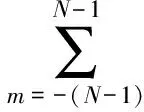
(7)
式中:χ1(td,0)為子脈沖的自相關函數,并且:
(8)
χ2(mτ,0)是歸一化偽隨機序列的非周期自相關函數。
2 噪聲移頻類靈巧干擾時頻分析模型
2.1 噪聲移頻類靈巧干擾
假設噪聲移頻函數為:
(9)
式中:n(t)為噪聲信號;KFM為移頻系數。
則噪聲移頻類靈巧干擾表示為:
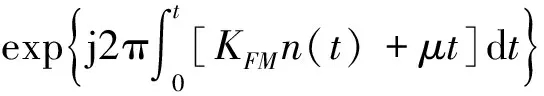
(10)
由上式可見,噪聲移頻類靈巧干擾本質上是雷達信號與噪聲調頻信號的乘積,即:
(11)
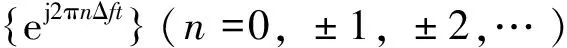
(12)
經推導可得最小均方誤差的系數an應為:
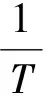
(13)
最小均方誤差為:
(14)
則式(10)可分解為:
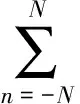
(15)
可見,噪聲移頻類靈巧干擾本質上可以看作2N+1個頻移量為nΔf固定移頻干擾的加權疊加。
2.2 短時傅里葉分析方法
1977年Allen給出了短時傅里葉變換(STFT)的定義[8]:
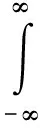
(16)
可見,z(t′)的短時傅里葉變換可以看作是z(t′)乘上1個以時間t為中心的“分析窗”γ*(t′-t)的傅里葉變換。
利用上面的原理對線性調頻信號與二相編碼信號通過匹配濾波器前后進行時頻特性的仿真,結果如圖1、圖2所示。
3 噪聲移頻類靈巧干擾特征提取
3.1 線性調頻信號噪聲移頻靈巧干擾仿真
下面對線性調頻信號噪聲移頻靈巧干擾的時頻域聯合分布仿真,假設信號的時寬T=50 μs,頻帶寬度B=5 MHz,工作頻率f0=10 MHz,用50 MHz頻率進行采樣,采用高斯白噪聲移頻調制,干擾增益10 dB,結果如圖3所示。
由圖3可見噪聲移頻類靈巧干擾使回波信號出現了密集的假目標,假目標出現的位置與移頻量fd解得的時間是對應的。另外,也可以發現干擾峰值比回波峰值要低一些。所以移頻調制對線性調頻信號的干擾特征為在真實回波范圍產生密集的距離假目標,達到欺騙性的壓制干擾效果。
由圖1、圖3可知,移頻調制類靈巧干擾的頻譜寬度比不移頻時略有減小,在時域上比真實目標要有所超前,這是由于進行了移頻處理,使信號不再與濾波器匹配,從而使干信比降低,移頻量過大對靈巧干擾效果不利。
3.2 二相編碼信號噪聲移頻靈巧干擾仿真
下面對二相編碼信號噪聲移頻靈巧干擾的時頻域聯合分布進行仿真驗證,仿真信號參數設置為時寬T=169 μs,子脈沖寬度τ=1 μs,信號形式為13×13組合巴克碼,載波中心頻率f0=2 MHz,采樣頻率20 MHz,采用高斯白噪聲移頻調制,干擾增益10 dB,結果如圖4所示。
由圖4可見,噪聲移頻干擾使回波信號的旁瓣電平有所抬升,并且當移頻量增大時主瓣也會惡化。所以,靈巧干擾對二相編碼信號的干擾效果主要表現為使回波主瓣和旁瓣的結構發生變化,影響對目標的距離分辨能力。
由圖2、圖4可知噪聲移頻類靈巧干擾可使二相編碼信號的回波周圍出現大量雜亂分布的干擾點,并且由于二相編碼信號的多普勒敏感性導致回波主瓣和旁瓣的結構也產生了嚴重的崎變。
4 結束語
靈巧干擾以其技術的先進性和干擾的靈活性必將在未來電子對抗中發揮出越來越重要的作用。本文采用時頻分析的基本方法——短時傅里葉變換來提取出噪聲移頻類靈巧干擾的特征,仿真信號參數對干擾效果的影響,有利于解決新型電子對抗系統探索和設計中的相關問題,進一步推動靈巧干擾技術的發展,在軍事領域具有十分廣闊的應用前景。
[1] SCHLEHER D C.Electronic Warfare in The Information Age [M].Boston,American:Artech House,1998.
[2] BAUMELA L,MARAVALL D.Real-time target tracking[J].IEEE Transactions on AES,1995,10(7):947-955.
[3] GRIIFFTHS H D.New ideas in FM radar[J].IEE Electronics and Communication Engineering Jounnal,1990,2(5):185-194.
[4] 王雪松,肖順平,馮德軍,等.現代雷達電子戰系統建模與仿真[M].北京:電子工業出版社,2010.
[5] 邱杰.靈巧噪聲干擾本質含義探討[J].海軍航空工程學院學報,2011,26(5):481-484.
[6] 周政,唐宏,張永順,王春陽.基于時域采樣的靈巧噪聲干擾研究[J],現代雷達,2010,32(5):53-55.
[7] 寧斐,唐斌.一種靈巧式欺騙干擾原理及實現[J].微計算機信息,2008,24(18):74-76.
[8] 董建華,顧漢明,張星.幾種時頻分析方法的比較及應用 [J].工程地球物理學報,2007,4(4):312-316.
FeatureExtractionofSmartNoiseFrequency-shiftJammingBasedonShort-timeFourierTransform
GONG Jian1,2,ZHANG Lei3,CHENG Chen4,XIONG Wu5
(1.Xidian University,Xi'an 710071,China;2.Air Force Engineering University,Xi'an 710051,China; 3.Unit 66133 of PLA,Beijing 100043,China;4.Unit 93792 of PLA,Langfang 065000,China; 5.Unit 94907 of PLA,Nanchang 330013,China)
The smart jamming has both characteristics of suppression jamming and deception jamming.The main technique indexes are about the characteristics of instantaneous change and random creation.As a conventional tool of signal processing,Fourier transform is only adapted to determined signal and smooth signal,and can not perform effective analysis to smart jamming.Aiming at the problem,this paper uses short time Fourier transform to extract the characteristics of smart noise frequency-shift jamming,simulates the influence of signal parameters on jamming effect,educes some conclusions that can help the research and countermeasure of new synthetical electronic jamming system.
smart jamming;time frequency analysis;noise frequency shift;short-time Fourier transform
2017-01-21
國家自然科學基金,項目編號:61601502;航空基金,項目編號:20150196007,20150196003,20160196003
TN972.2
:A
:CN32-1413(2017)03-0001-04
10.16426/j.cnki.jcdzdk.2017.03.001

