超大型集裝箱船參數橫搖全面校核與安全評估

馬騁遠，馬寧，王廷昊，顧解忡

1上海交通大學船舶海洋與建筑工程學院，上海200240

2高新船舶與深海開發裝備協同創新中心，上海200240

3上海交通大學海洋工程國家重點實驗室，上海200240

超大型集裝箱船參數橫搖全面校核與安全評估

馬騁遠1，2，馬寧2，3，王廷昊1，2，顧解忡2，3

1上海交通大學船舶海洋與建筑工程學院，上海200240

2高新船舶與深海開發裝備協同創新中心，上海200240

3上海交通大學海洋工程國家重點實驗室，上海200240

［目的］由于超大型集裝箱船在波浪中穩性高的變化較為顯著，對其參數橫搖校核與安全評估要求較高，因此，［方法］基于參數橫搖模式，針對在迎浪中航行的某10 000 TEU集裝箱船，對其各個裝載狀況逐一并逐級進行計算。自主開發基于典型弱非線性三自由度模型的數值預報方法，對不滿足第2層衡準要求的載況進行時域模擬，并綜合考慮航速、波況的影響，全面探索其可能發生參數橫搖的工況。［結果］根據衡準結果，得出相應的安全性評估與規避措施：降低重心高度、適當提高航速、盡量避免船舶橫搖固有周期約等于2倍遭遇周期等均能有效避免參數橫搖的發生。［結論］對10 000 TEU集裝箱船進行的參數橫搖全面校核評估能夠更好地指導超大型集裝箱船的總體設計，提高安全水平，具有較高的工程應用及參考價值。

超大型集裝箱船；參數橫搖；直接計算；安全性評估

0 引 言

國際海事組織（IMO）正在制定包括參數橫搖、純穩性喪失、騎浪/橫甩、癱船穩性和過度加速度這5種穩性失效模式的第2代完整穩性規則［1］。作為第2代完整穩性衡準中的一個重要部分，參數橫搖衡準的制定和實施將對船舶性能與設計產生重大影響［2］。對于在縱浪中航行的船舶，當橫搖固有周期接近2倍的遭遇周期，且入射波長范圍與船長尺度接近時，水線面積會隨波浪與船體的相對位置變化發生大幅波動，進而引起初穩性高GM的變化。此時，若船舶橫搖阻尼較小，在很小的初始橫向擾動下將會出現大幅橫搖運動，即發生參數橫搖現象［3-5］。這類情況多發生于漁船、客滾船和大型集裝箱船［6］。

根據參數橫搖的研究成果并考慮工程應用的方便，IMO將衡準劃分為了3個層次，即第1層衡準、第2層衡準和直接計算衡準。這3個層次的衡準被設計為從簡單的經驗公式到采用單自由度非線性力學方法，直至采用較為復雜的三自由度及以上運動數值模擬手段預報參數橫搖，依次提高復雜程度并預報精度［7］。在實船設計中，僅當設計方案無法通過低層次衡準時才需要進行更高層次的衡準計算。

大型集裝箱船對于參數橫搖比較敏感，從對包括APL CHINA號（C11集裝箱船）在內的若干實船事故的調查報告可以發現［5］，大幅橫搖甚至是傾覆所帶來的人員傷亡與財產損失將更為慘重。傅超等［8］結合第2代完整穩性參數橫搖前2層衡準和七〇二所開發的穩性評估軟件平臺，就舭龍骨面積與重心高度對C11集裝箱船的參數橫搖敏感因素進行分析，并對船艏和船艉的型線進行改進，達到了改善參數橫搖的目的。但對此類船型開展3個層次的全面校核工作的并不多。因此，在遠洋貨輪航行安全性更受關注的當代，對萬箱級集裝箱船舶進行安全性評估的意義將顯得格外突出，也可以更好地指導超大型集裝箱船總體設計，為提高安全水平提供更具基礎性的研究。

IMO參數橫搖第2代完整穩性規則預計將于2019年定稿，其中第1、第2層衡準規則已趨成熟，公式體系也已逐漸被眾多研究機構所認可。Umeda等［9］將參數橫搖簡化為單自由度橫搖運動模型，其中非線性回復力采用與波陡相關的非線性函數進行表達。梁海濱等［2］基于參數橫搖衡準，采用多元線性回歸方法計算了靜水中的回復力系數，并運用二分法求解橫搖幅值，根據對某漁政船的計算結果，為其航行安全性提供了操作指導。但是對于第3層衡準，不同計算方法與模型的提案較多，且依舊處于樣船計算階段，還未形成較為系統與完整的衡準框架。因此在定稿前，豐富第3層衡準的樣船信息與校核資料就變得十分具有研究價值。

針對此，Bulian［10］考慮通過靜水力計算得到的垂蕩和縱搖運動對參數橫搖的影響，提出一種1.5自由度模型，得到了一種較為準確的參數橫搖時域模擬方法。Spanos和 Papanikolaou［11］采用基于脈沖響應函數法的六自由度模型對漁船和滾裝船進行了數值模擬，結果顯示橫搖與縱搖耦合，非線性回復力對參數橫搖計算結果影響較大。Sadat-Hosseini等［12］采用 CFD 方法研究了一艘水面艦艇的參數橫搖問題，發現在迎浪下模擬結果與實驗結果吻合較好，但采用CFD計算耗時巨大。

本文擬根據在迎浪中航行的某10 000 TEU集裝箱船的裝載及穩性計算書，對各個裝載工況逐一進行計算。先對第1層衡準進行判定，若不符合要求，則需要進行第2層衡準的1stcheck與2ndcheck判定。鑒于參數橫搖的強非線性，其受橫搖阻尼、非線性回復力計算等因素的影響較大，又考慮到工程實際問題計算的相對簡便與實用性，提出并自主研發了基于典型的弱非線性三自由度（橫搖、垂蕩和縱搖）模型，以對不滿足第2層衡準要求的載況進行迎浪規則波中的參數橫搖時域模擬。最后，將對10 000 TEU集裝箱船在不同航速、波高和波頻時發生參數橫搖的情況進行數值模擬，并分析敏感工況的特征，進行航行安全性評估，提出規避措施。

1 IMO參數橫搖第1 層薄弱性衡準

第1層衡準基于經驗公式［7］。若一艘船滿足以下條件，則可判定該船對于參數橫搖不敏感：

式中：ΔGM為當波浪通過船體時船舶穩性高的變化幅度；GM為船舶在靜水條件下計算所得載況的初穩性高；RPR為標準值，具體計算公式如下：

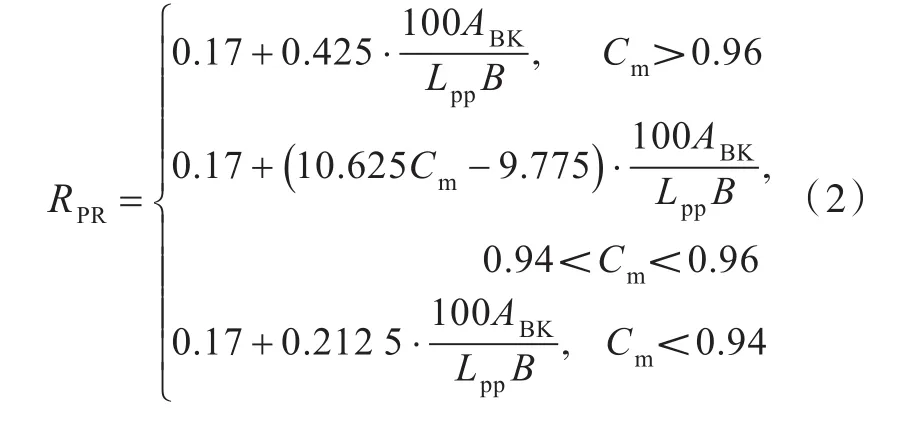
式中：Cm為舯橫剖面系數；ABK為不計入附體的舭龍骨側投影面積之和，m2。

10 000 TEU集裝箱船的主尺度如表1所示。

表1 10 000 TEU集裝箱船主尺度Table 1 Main dimensions of 10 000 TEU container ship

校核計算結果如圖1和圖2所示。經對比可知，對于吃水較小（d＜10 m）的空船以及各種情形下的壓載工況，其重心高度遠低于載況，GM值較大（GM＞12 m），ΔGM/GM計算值較小，更容易通過衡準。

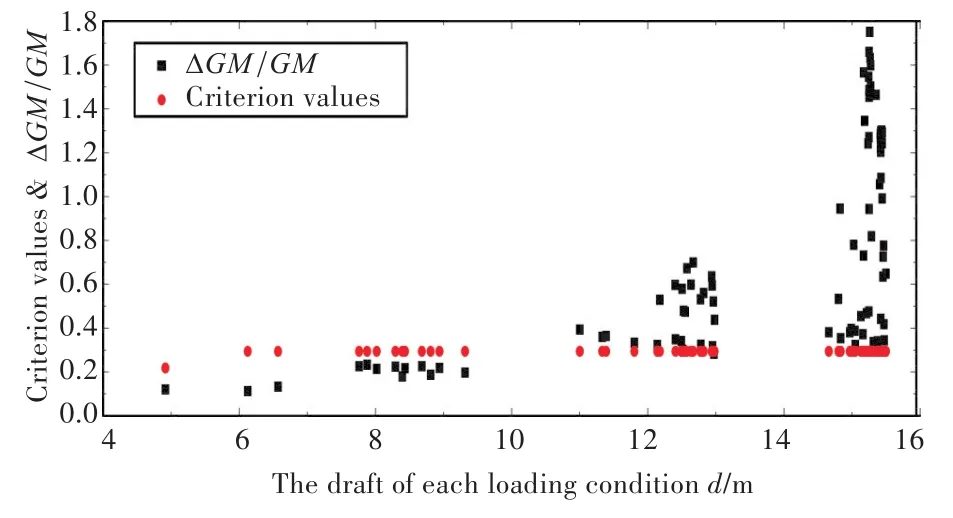
圖1 參數橫搖第1層薄弱性衡準結果Fig.1 The first level criterion results of parametric roll

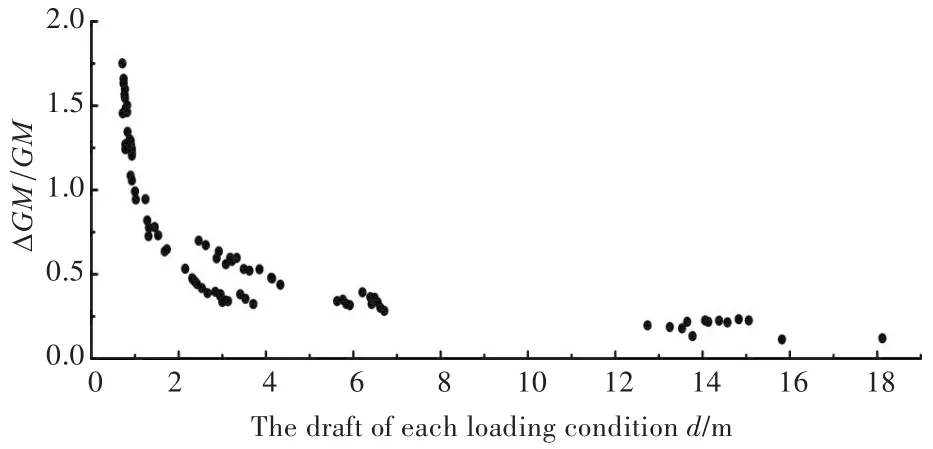
圖2 ΔGM/GM隨初穩性高GM的變化Fig.2 Variation of ΔGM/GMwithGM

對于吃水d較大的載況，GM的值主要取決于重心G的高度，即甲板上集裝箱裝載的層高。研究表明，集裝箱布置層高越低，整船重心越低，GM越大，ΔGM/GM計算值越小，參數橫搖第1層衡準校核通過率越高。在不改變集裝箱布置形式的前提下，亦可通過將重型集裝箱盡可能往貨艙堆積，輕型集裝箱往甲板堆放的方式來降低全船重心。

經計算校核，在10 000 TEU集裝箱船的89個載況中，有14個載況通過了參數橫搖第1層薄弱性衡準，剩余的75個載況未通過，需要進行第2層衡準。

2 IMO參數橫搖第2 層薄弱性衡準

根據參數橫搖草案［7］，用于實船敏感性預報的入射波條件采用國際船級社協會（IACS）推薦的不規則波散布圖，所有海況將采用Grim［13］的等效波理論換算為等效規則波。第2層薄弱性衡準相對于第1層衡準更加嚴密。若一艘船舶滿足以下任意一個條件，可以認為其不會發生參數橫搖：

1）1stcheck計算所得的C1值小于RPR0；

2）1stcheck計算所得的C1值大于RPR0，且2ndcheck所得的C2值小于RPR1。

2.1 1stcheck算法

1stcheck算法通過對第1層衡準的入射波條件進行拓展，通過對若干等效規則入射波進行加權計算，確定船舶對于參數橫搖的敏感性指數。

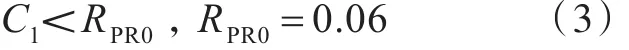
式中：C1為敏感性指數；RPR0為1stcheck標準值。當滿足式（3）的條件時，認為船舶能夠滿足1stcheck的要求，具體計算過程參見文獻［9］。

2.2 2ndcheck算法

2ndcheck采用了基于非線性力學方法的單自由度（1-DOF）橫搖運動方程，用于參數橫搖幅值的預報，并在此基礎上進行敏感性分析。運動方程為

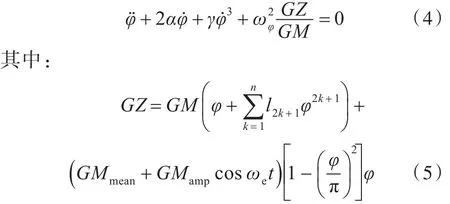
式中：φ為船舶橫搖角；GMmean為波浪中穩性高變化的平均值；GMamp為波浪中穩性高變化量的幅值；ωφ為橫搖固有圓頻率；ωe為遭遇頻率；l2k+1為采用最小二乘法擬合靜水中的GZ曲線得到的擬合系數，其中k為擬合階數；α，γ分別為線性和三次橫搖阻尼系數，對于缺乏橫搖衰減試驗結果的情況，可采用簡化的Ikeda方法［14］計算。

對于不同的傅汝德數Fr，在頂浪狀態下，計算船舶橫搖角度超過25°的概率，取概率的平均值即得到敏感性指數C2。若

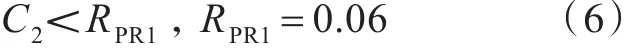
則判定船舶校核的該載況對于參數橫搖現象不敏感。

C2的計算公式為

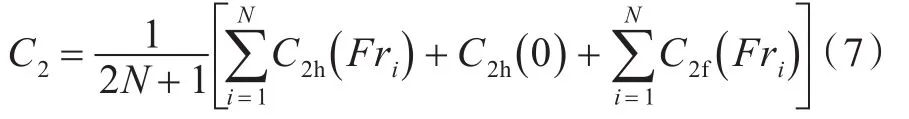
式中，C2h(Fri)和C2f(Fri)分別為以Fri迎浪和隨浪航行時C2的分量。其中，Fri的取法如下：

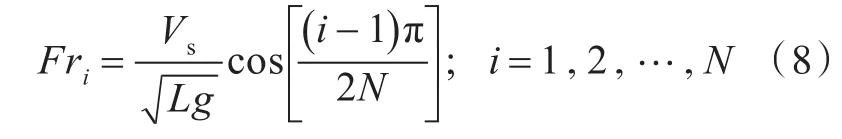
式中：L為船長；g為重力加速度；Vs為服務航速；N為浪向間距數，IMO最新建議取N=3［15］。

2.3 校核結果

經過第1層薄弱性衡準的校核與篩選，將剩余未通過的75個載況進行第2層衡準，分別進行1stcheck與2ndcheck的計算。

1stcheck校核計算結果如圖3所示。結果的分布基本上呈現出GM值越大，計算值C1也越大的情況。

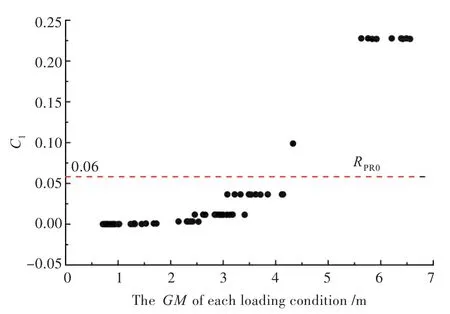
圖3 參數橫搖第2層衡準1stcheck校核計算結果Fig.3 The second level criterion 1stcheck results of parametric roll

2ndcheck校核計算結果如圖4所示。結果顯示，75個載況的敏感性指數C2均小于RPR1=0.06。

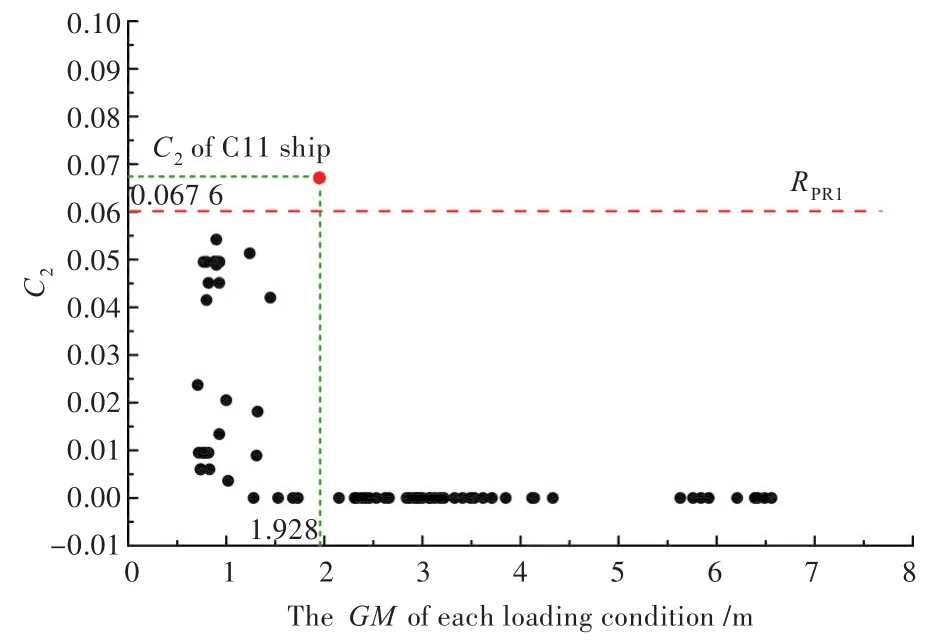
圖4 參數橫搖第2層衡準2ndcheck校核計算結果Fig.4 The second level criterion 2ndcheck results of parametric roll

對于初穩性高大于4.33 m的10個載況，圖3中的計算顯示，其雖然未通過1stcheck的衡準要求，但在2ndcheck的校核計算中，它們的敏感性指數C2均為0，因此可以認為它們對參數橫搖并不敏感。

另外，由于APL CHINA號（C11集裝箱船）在太平洋海域開展商業運營的航行中發生了嚴重的參數橫搖事故［5］，因次，C11船成為IMO制定參數橫搖衡準失效模式的唯一標準樣船。本文選取C11船設計吃水載況（吃水d=11.5 m，初穩性高GM=1.928 m）下計算結果C2（C2=0.067 6）與本船的校核結果進行了橫向對比（圖4），發現本船各載況下的C2值均小于C11船對應的結果。

對于靜水中GZ曲線的擬合（式（5）），其擬合范圍為從正浮至30°橫傾角的部分，GZ曲線的計算以2°為間距，擬合誤差應小于5%或0.005 m中的較大值［15］。但經過計算發現，載況14TAS（14T/TEU Arrival at Scantling Draft）的靜水GZ曲線在6°，8°，10°的擬合誤差分別為 5.98%，5.51%和5.43%，未達到精度要求，因此該載況未通過參數橫搖第2層衡準，需要進行直接計算。同時，因該載況接近滿載，GM=1.24 m，C2=0.051 3，較接近衡準值0.06，偏于危險，因此有必要繼續對其進行直接計算衡準。

3 參數橫搖直接計算相關理論

目前，IMO對于參數橫搖直接衡準計算的規則尚未完成制定，僅給出了用于直接計算衡準運動的初步要求指南［16］。

本節將采用基于勢流理論方法的弱非線性時域三自由度運動預報模型作為直接計算衡準的校核方法。該方法在三維頻域勢流方法的基礎上應用了脈沖響應函數理論，并采用三維壓力積分方法考慮了由船體瞬時濕表面積所引起的Froude-Kriloff力和回復力的非線性效應。運動方程式［17］如下：

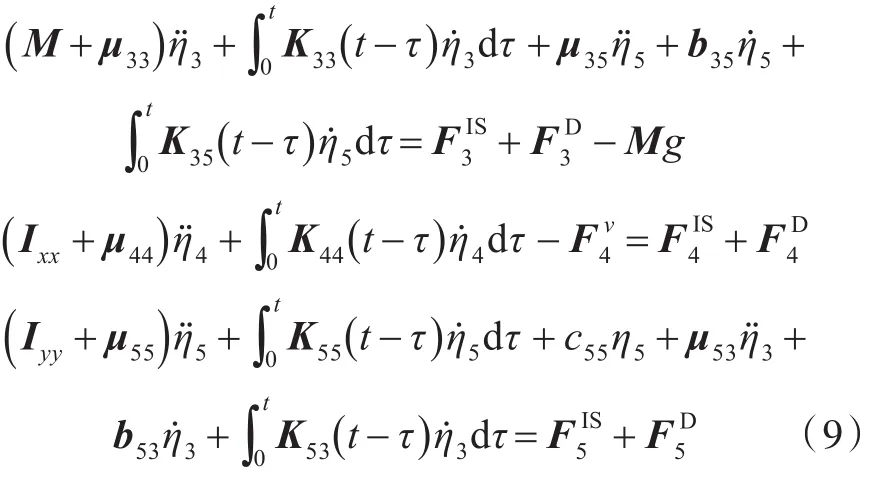
式中：M和Ixx，Iyy分別為船舶質量和慣性矩；η3，η4，η5分別為船舶的垂向位移、橫搖角和縱搖角；c55為縱搖回復力系數；g為重力加速度；t為時間；τ為時間被積參數；μjk（j，k=1，2，3，分別代表垂向、橫向和縱向）為附加質量和附加慣性矩，在平均濕表面下求解三維邊值問題得到；為橫搖粘性阻尼力矩，采用Ikeda方法［14］進行計算；FIS為Froude-Kriloff力與回復力的合力，基于三維壓力積分方法計算，且考慮了由船體瞬時濕表面積所引起的非線性效應；輻射力（積分項）和繞射力FD的計算基于三維頻域線性水動力方法，輻射力中Kjk的計算基于脈沖響應函數理論，以考慮時延效應

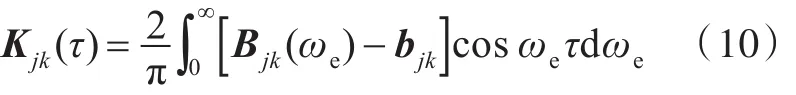
式中：Bjk(ωe)為頻域理論計算的興波阻尼；bjk為對輻射力應用脈沖響應函數理論引起的阻尼項。

4 計算載況與工況

4.1 計算裝載

第2節末已提及，14TAS載況由于其GZ曲線的擬合精度不滿足第2層衡準的要求，且其敏感性指數C2的計算值接近衡準值，偏于危險，因此需要進行第3層的直接計算。本載況的相關浮態信息如表2所示。

表2 14TAS裝載工況浮態信息Table 2 Floating information about loading condition 14TAS

4.2 計算參數與工況設置

計算參數中，Fr從小到大依次選取值為0.05，0.1和0.218（對應的Vs=23.75 kn）。對于入射的規則波，在選取波長時考慮到了3種形式：

1）波長等于船長（λ=Lpp），波陡的選擇參考參數橫搖第1和第2層衡準［7］，對應每種航速下的1～2號工況。

2）根據參數橫搖發生的充分條件（船舶的橫搖固有周期約等于2倍的波浪遭遇周期Tφ≈2Ti）與波浪色散關系（，其中ωwave為波頻，kwave為波數）換算得到波長，波陡的選擇參考參數橫搖第1和第2層衡準［7］，對應每種航速下的3～6號工況。

3）Grim［13］等效入射波浪表中權重占比（根據北大西洋波浪統計數據顯示不同波況出現的概率）最大的規則波（λ=287.931 m，H=4.031 m），對應每種航速下的7號工況。

5 直接計算結果與討論

5.1 瞬時濕表面積分程序驗證

本研究中，參數橫搖數值模擬程序采用基于NURBS曲面的瞬時濕表面壓力積分法來計算非線性回復力和Froude-Kriloff力。

船舶在波浪中水線面積的變化是參數橫搖發生的重要原因，主要由初穩性高GM的變化導致。因此，本文采用程序計算了10 000 TEU集裝箱船在14TAS載況時與波浪不同相對位置下的GM值，并與通用軟件NAPA的計算結果進行了對比，如圖5所示。由圖可見，兩者的結果相差較小，進一步驗證了基于NURBS曲面的瞬時濕表面壓力積分程序的準確性與有效性。

圖5GM隨船體與波浪相對位置的變化情況Fig.5 Variation ofGMwith hull and waves'relative position

5.2 校核結果與分析

采用上述波浪條件與航速設置的組合形式進行典型工況的數值模擬分析，輸出三自由度（垂蕩、橫搖、縱搖）時歷曲線，給定初始擾動橫搖角為0.2°，模擬時長1 200 s。表3所示為不同工況下參數橫搖的計算結果，其中，若干算例的“傾覆”被定義為橫搖角在某時刻超過了90°。

對于波長等于船長（λ=Lpp=320 m）的工況Ⅰ-1，Ⅰ-2，Ⅱ-1，Ⅱ-2，Ⅲ-1和Ⅲ-2，波陡的取值合理，僅在Fr=0.05低航速的2個工況（Ⅰ-1，Ⅰ-2）出現了微幅的參數橫搖現象。工況Ⅰ-2下的三自由度時域模擬曲線如圖6所示。從中可以看出，在400 s時橫搖開始顯現并逐漸增大，600 s后，趨于穩定幅值（2.98°）下的參數橫搖、垂蕩與縱搖運動在后期在小范圍內穩定振蕩。

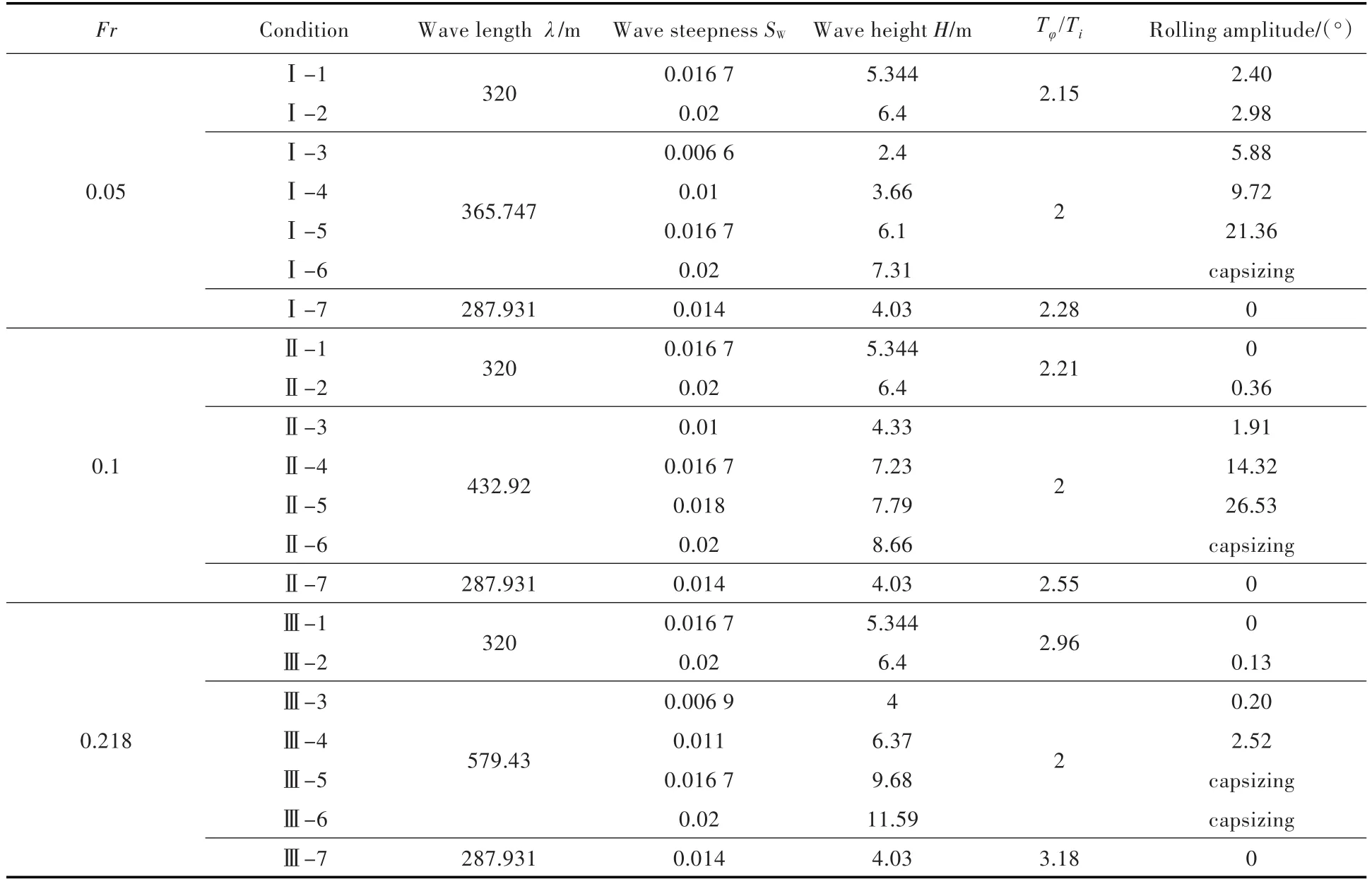
表3 規則波下不同工況參數橫搖計算結果表Table 3 Parametric roll results of different conditions in regular waves

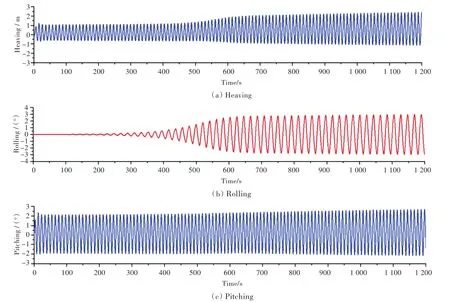
圖6Ⅰ-2工況下的垂蕩、橫搖、縱搖時歷曲線Fig.6 Time history curves of heaving，rolling and pitching at conditionⅠ-2

當橫搖固有周期約等于波浪遭遇周期的2倍時，更易發生參數橫搖，在相似波高下，橫搖幅值遠大于λ=Lpp的波況。圖7所示為Ⅱ-6工況下的三自由度時域模擬曲線。由圖可見，在時域模擬的前、中期，垂蕩與縱搖較為劇烈，橫搖微弱；在倍頻關系與較大波高的聯合激勵下，600 s后，垂蕩與縱搖開始出現強非線性效應，橫搖亦不斷增大，直至800 s后出現傾覆。對這2個工況（Ⅰ-2和Ⅱ-6）而言，出現顯著參數橫搖的時間均較晚。

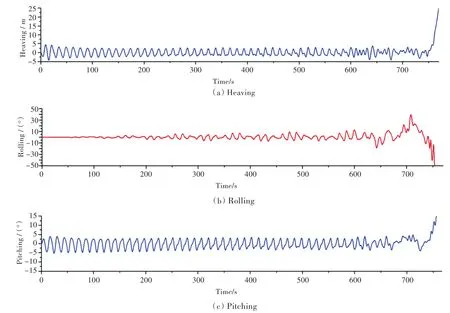
圖7 Ⅱ-6工況下的垂蕩、橫搖、縱搖時歷曲線Fig.7 Time history curves of heaving，rolling and pitching at conditionⅡ-6

5.3 直接計算衡準中危險工況的特征分析

根據表3的計算結果不難發現，當船舶處于迎浪規則波條件下航行，且在規則波波長滿足λ=Lpp入射時，10 000 TEU集裝箱船從低到高的3個航速對參數橫搖均顯示出不敏感；而當規則波波長滿足其橫搖固有周期約等于2倍的波浪遭遇周期時，參數橫搖的發生最為明顯，事實上這也是參數橫搖發生的條件之一。

圖8所示為在入射波滿足倍頻關系的條件下，不同航速時，發生參數橫搖的橫搖幅值隨波陡與波高的變化情況。對參數橫搖的直接計算，一般認為在較長時間的時域模擬中，船舶橫搖角超過25°即發生了參數橫搖［17］，因此在圖8中給出了各航速下發生參數橫搖的臨界波陡與臨界波高。

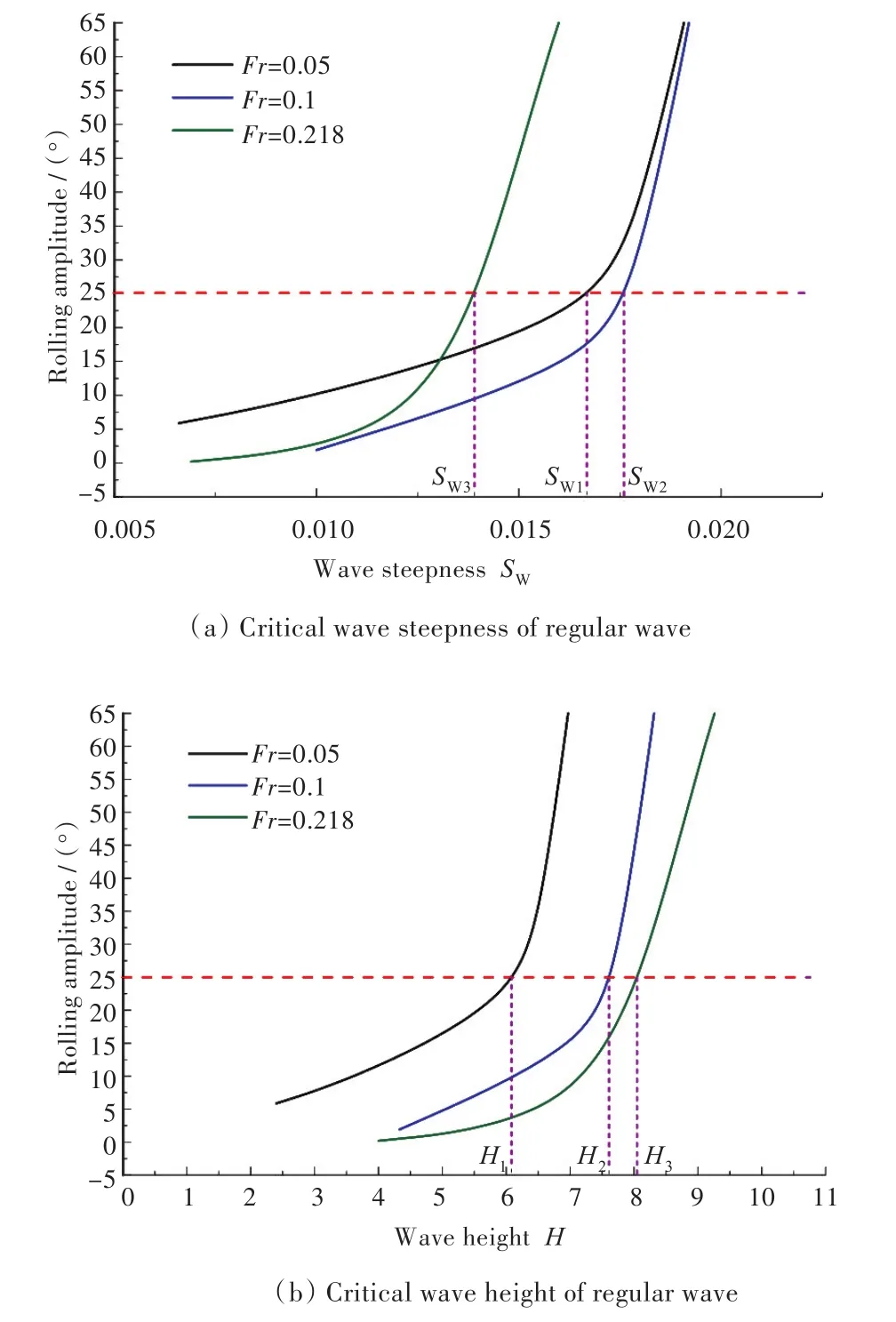
圖8 不同航速下橫搖幅值隨波陡與波高的變化（Tφ≈2Ti）Fig.8 Variation of amplitude of rolling with wave steepness and wave height at different speeds（Tφ≈ 2Ti）

由圖可以發現，當以臨界波陡作為標準分析各工況參數橫搖的敏感性時，不同航速下臨界波陡值的分布缺少規律；而當以臨界波高為標準分析時，臨界波高與航速的分布具有較好的相關性，因此，應以波高條件作為超大型集裝箱船參數橫搖衡準計算時危險工況的選擇標準。當船舶處于低航速（Fr=0.05）時，發生參數橫搖的臨界波高相對較小（H=6.2 m），屬于相對危險工況，且相比其他航速，此時對應的入射波波長與Grim［13］的等效入射波浪表中權重占比最大的規則波最為接近，意即更加接近實海域條件。

5.4 實海域航行安全性評估

基于弱非線性時域三自由度運動預報模型，對于10 000 TEU集裝箱船而言，低航速對參數橫搖現象的發生更加敏感。在實際航行過程中，若遇長波高幅的連續規則涌浪，則需要提高航速，避開倍頻區間，以保持在橫向干擾小的縱浪下航行，避免大幅橫搖。

實際上，對14TAS載況參數橫搖的危險性評估相對來說較為保守。首先，計算所得的敏感工況幾乎都滿足倍頻條件；其次，只有當航速較低且大于臨界波高時才有機會發生參數橫搖。實際航行中若遇此惡劣海況，駕駛員需要更改艏向至迎浪，必要時，需要采取減速停船、集裝箱穩固綁扎等相應的措施來避免失穩或傾覆。

危險工況中出現的大幅參數橫搖現象幾乎都發生在時域模擬的后期，且前、中期已經開始逐漸顯現橫搖增大的現象。此時，考慮到參數橫搖的情形，駕駛員需按航行手冊與操作指南及時采取相應的規避措施，以避免橫搖的進一步增大。而降低重心高度、適當提高航速、盡量避免波浪倍頻關系的滿足等均能有效規避參數橫搖的發生。

6 結論

鑒于超大型集裝箱船對參數橫搖安全性評估要求較高，校核意義突出，本文以一艘10 000 TEU集裝箱船實船為研究對象，對其各載況進行了IMO第2代完整穩性的參數橫搖薄弱性全面校核計算，得到以下主要結論：

1）根據第1層衡準結果，降低船舶重心高度可顯著減小波浪中穩性高的變化幅度，對改善參數橫搖作用明顯。

2）參考第2層衡準的結果，對于初穩性高GM越大的載況，敏感性指數C1也越大；敏感性指數C2較大載況的GM值分布在約1 m外。

3）隨著波陡的增加，由于波浪中回復力變化大，參數橫搖幅值也變大。對于滿足倍頻關系的危險波況，需要針對特定的船舶選擇不同航速下的臨界波高作為校核的計算取值。

4）航速對參數橫搖的影響較大，根據直接計算結果，航速增大在一定程度下會對參數橫搖存在抑制作用。

5）Grim［13］的等效入射波浪表為基于北大西洋波浪的統計數據，在迎浪狀態下，對于其中權重占比最大的規則波，10 000 TEU集裝箱船在3個航速下對參數橫搖均不敏感。

［1］International Maritime Organization（IMO）.Develop?ment of second generation intact stability criteria［C］//Sub-committee on stability and load lines and on fish?ing vessels safety（SLF）55th session.London：Interna?tional Maritime Organization，2013.

［2］梁海濱，馬坤.基于參數橫搖的航行安全性研究［J］.中國造船，2015，56（增刊1）：185-192.LIANG H B，MA K.Research of navigation safety based on parametric roll［J］.Shipbuilding of China，2015，56（Supp 1）：185-192（in Chinese）.

［3］DALLINGA R P，BLOCK J J，LUTH H R.Excessive rolling of cruise ships in head and following waves［C］//RINA International Conference on Ship Motions&Ma?neuverability.London，UK：［s.n.］，1998.

［4］CHU J L，WU C S，LU J，et al.Study on a 3D time-domain method to predict parametric rolling of a ship in regular head seas［J］.Journal of Ship Mechan?ics，2016（12）：1513-1522.

［5］FRANCE W N，LEVADOU M，TREAKLE T W，et al.An investigation of head-sea parametric rolling and its influence on container lashing systems［J］.Marine Technology，2003，40（1）：1-19.

［6］LEVADOU M，VEER R V.Parametric roll and ship de?sign：contemporary ideas on ship stability and capsiz?ingin waves［M］.Netherlands：Springer，2011：307-330.

［7］International Maritime Organization（IMO）.SDC 1/INF.8.Information collected by the correspondence group on intact stability regarding the second genera?tion intact stability criteria development［C］//Ship De?sign and Construction（SDC）1st Session.London：In?ternational Maritime Organization，2013.

［8］傅超，馬山，段文洋，等.C11集裝箱船參數橫搖發生敏感性因素分析和改善措施研究［C］//2014年全國船舶穩性學術研討會論文集.無錫：中國造船工程學會，2015.

［9］UMEDA N，HASHIMOTO H，VASSALOS D，et al.Nonlinear dynamics on parametric roll resonance with realistic numerical modelling［J］.International Ship?building Progress，2004，51（2/3）：205-220.

［10］BULIAN G.Nonlinear parametric rolling in regular waves—a general procedure for the analytical approxi?mation of the GZ curve and its use in time domainsimulations［J］.Ocean Engineering，2005，32（3/4）：309-330.

［11］SPANOS D，PAPANIKOLAOU A.Numerical simula?tion of parametric roll in head seas［J］.International Shipbuilding Progress，2007，54（4）：249-267.

［12］SADAT-HOSSEINI H，STERN F，OLIVIERI A，et al.Head-wave parametric rolling of a surface combatant［J］.Ocean Engineering，2010，37（10）：859-878.

［13］GRIM O.Beitragzudem problem der sicherheit des schiffesimseegang［J］.Shiff und Hafen，1961，6：490-497（in German）.

［14］KAWAHARA Y，MAEKAWA K，IKEDA Y.A simple prediction formula of roll damping of conventional car?go ships on the basis of Ikeda's method and its limita?tion［C］//Proceedings of the 10th International Confer?ence on Stability of Ships and Ocean Vehicles.Neth?erlands：Springer，2009：387-398.

［15］International Maritime Organization（IMO）.Finaliza?tion of second generation intact stability criteria，amendments to Part B of the 2008 IS code on towing，lifting and anchor handling operations［C］//Ship De?sign and Construction（SDC）3rd session.London：In?ternational Maritime Organization，2016.

［16］International Maritime Organization（IMO）.Informa?tion collected by the correspondence group on intact stability regarding the second generation intact stabili?ty criteria development［C］//Ship Design and Con?struction（SDC）1st session.London：Internation Mar?itime Organization，2014.

［17］周耀華，馬寧，顧解忡.集裝箱船橫搖慣性矩計算方法對參數橫搖敏感性預報影響研究［J］.中國造船，2013，54（3）：11-20.ZHOU Y H，MA N，GU X C.Effect of calculation methods of roll moment of inertia on sensitivity predic?tion of parametric rolling for container ships［J］.Ship?building of China，2013，54（3）：11-20（in Chinese）.

Comprehensive calculation and safety assessment of parametric roll of very large container ship

MA Chengyuan1，2，MA Ning2，3，WANG Tinghao1，2，GU Xiechong2，3
1 School of Naval Architecture，Ocean&Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China
2 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China
3 State Key Laboratory of Ocean Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

As the significant variation of GM in waves for very large container ships,strict demands are raised for this ship type in the evaluation and safety assessment of parametric roll.Targeting a 10 000 TEU container ship sailing in head sea,this study conducts a series of calculations and evaluations on parametric roll motion in which each loading condition is calculated step-by-step.Direct calculation is conducted if neither Level 1 nor Level 2 is satisfied.In this paper,an independently developed time-domain simulation is conducted for loading conditions that fail to match the Level 2 criteria,which is based on a typical 3-DOF weakly nonlinear numerical model.Ship velocity and wave conditions are taken into consideration to explore sensible conditions concerning parametric roll.Finally,according to the results,corresponding safety assessments and several avoidance measures are proposed,such as reducing the height of the center of gravity and raising the speed moderately.In addition,if wave predictions can be detected in advance,the circumstance of the natural rolling period being twice as great as the encountering period should be avoided,which isthe most sensible factor for inducing parametric roll.Comprehensive calculation and checking for the 10 000 TEU ship can instruct the general design and improve safety for very large container ships;as a result,remarkable engineering applications and reference value can be recognized.

very large container ship；parametric roll；direct calculation；safety assessment

U661.32

：ADOI：10.3969/j.issn.1673-3185.2017.03.002

http://kns.cnki.net/kcms/detail/42.1755.TJ.20170512.1301.038.html期刊網址：www.ship-research.com

馬騁遠，馬寧，王廷昊，等.超大型集裝箱船參數橫搖全面校核與安全評估［J］.中國艦船研究，2017，12（3）：7-15.

MA C Y，MA N，WANG T H，et al.Comprehensive calculation and safety assessment of parametric roll of very large container ship［J］.Chinese Journal of Ship Research，2017，12（3）：7-15.

2016-11-28< class="emphasis_bold">網絡出版時間

時間：2017-5-12 13:01

財政部、教育部重大科研專項基金資助項目（GKZY010004）；國家自然科學基金資助項目（51579144）

馬騁遠，男，1992年生，碩士生。研究方向：波浪中的船舶穩性與安全性設計。E-mail：sjtumcy@163.com

馬寧（通信作者），男，1961年生，博士，教授，博士生導師。研究方向：船舶與海洋結構物耐波性及安全性，海洋波浪數值模擬預報。E-mail：ningma@sjtu.edu.cn