模糊非參數統計檢驗及在老齡化社會調查領域的應用

王忠玉+吳柏林

摘 要：在社會科學研究中，許多事物的測算或觀測結果往往不是精確的數據，而是或多或少具有模糊屬性的數據。中國人口老齡化問題越來越突出，至2015年底，我國60周歲及以上老年人口數量為22 182萬，占總人口16.15%。關注老年人的生活議題顯得十分重要。在研究老年人問題時，因研究對象都曾經歷不同時空背景與人生閱歷，個體間存在的差異極大，如何準確獲得有關老年人的生活、醫療等信息，為國家和政府決策提供真實客觀的信息，則是一項緊迫的任務。依據老年人身的身心發展特質，探索利用模糊理論的軟計算，設計出模糊數據調查表，提出反模糊化變換。同時，運用中位數檢驗及方差檢驗，建立統計參數為模糊數或模糊區間時的小樣本非參數模糊統計檢驗方法，并給出具體調查事例加以說明。

關鍵詞：模糊數據；反模糊化變換；模糊非參數統計檢驗；老齡化社會

中圖分類號：F24 文獻標志碼：A 文章編號：1673-291X（2017）17-0001-10

一、刻畫模糊性的模糊理論

1.模糊理論

模糊理論源于1965年美國伯克利（Berkeley）大學L.A.Zadeh教授在《信息與控制（Information and Control）》期刊上所發表的論文。模糊集合（Fuzzy sets）理論至今已有60多年的發展歷史。

模糊理論是以模糊集合為基礎，其基本思想是以模糊現象為研究對象。如何使用明確的數學方式表達模糊性呢？Zadeh簡單地將具有0與1兩個值的特征函數 IA（x）擴展成 [0，1]區間，稱此函數為隸屬度函數（membership function）。隸屬度函數在模糊理論上扮演著中心角色，它是從傳統集合的特征函數所衍生來的，以此刻畫元素對模糊集合的隸屬度，其范圍介于0到1之間。對于元素和集合的關系，傳統集合用特征函數描述，即當x∈A，則I（x）= 1；當x？埸A時，則I（x）= 0。Zadeh提出，當元素屬于某集合的程度越大，則其隸數度值越接近1，反之則越接近0。這樣方法可將介于“是”與“不是”之間的所有狀態表示出來了。

2.隸屬度函數

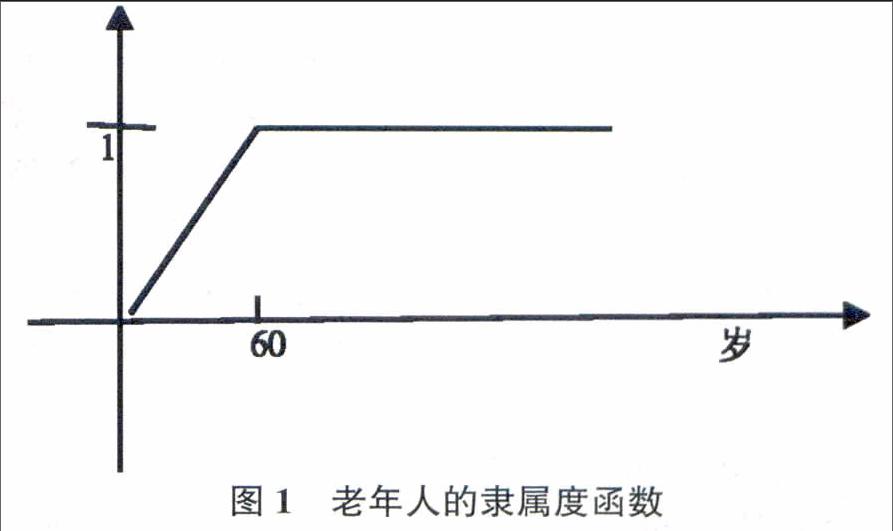
用傳統集合定義具有模糊性的語言變量時，常會造成許多不合理的現象。假如今天假設A、B、C三人，年紀各為59、60、75歲，其中A、B兩人雖只差1歲，只有B算老人，A卻不屬于老人。很明顯，這樣相當不合理。對于傳統的二分法與人類思維格格不入的問題，利用隸屬度函數能得到較合理的答案。如果某人認為70歲絕對屬于老年，則其隸屬度函數值自然為1，而59歲幾乎可算是老人，則其隸屬度函數值為0.9，此表示59歲屬于老年的程度有0.9。這樣，可繪出模糊集合老年人的隸屬度函數圖（圖1）。

和傳統集合的特征函數比較，隸屬度函數是將特征函數平滑化了。而且，隸屬度函數讓每個年齡層都擁有一個介于0到1之間的值，來代表人年老的程度。相較于傳統集合的特征值，在刻畫具有模糊性的事物概念時，用模糊集合的隸屬度函數來解釋更為適當。

通常，隸屬度函數可分為離散型與連續型兩類。離散型隸屬度函數是以窮舉法直接給定有限模糊集合內每個元素的隸屬度。而連續型隸屬度函數則是利用幾種常用的函數形式（s函數、z函數、Π函數、三角形函數、梯形函數、高斯（鐘型）函數）來描述模糊集合。在連續型隸屬度函數的形式中，以三角形、梯形、鐘形等隸屬度函數容易理解，并且能滿足大部分的研究設計。梯形隸屬度函數，因計算方便且貼近語意的模糊性，是本文所采用的。

隸屬度函數的設計與建立并不具有唯一性，關于年老概念的模糊集合用以如下的隸屬度函數描述之：

這樣的隸屬度函數可以完全表達出模糊集合，如μ年老表達出年老模糊集合的含義。

隸屬度函數是模糊理論最基本的概念，它不僅可描述模糊集合的性質，更可對模糊集合進行量化，并利用精確的數學方法來分析和處理模糊信息。要建立足以表達模糊概念的隸屬度函數，并不是一件容易的事。原因在于隸屬度函數的建立脫離不了個人主觀意識，故沒有通用定理或公式，一般是根據經驗或統計來加以建立。

二、模糊數與反模糊化變換

當統計參數為模糊數或模糊區間的情況時，很難利用傳統統計檢驗方法處理。當收集到模糊數或模糊區間樣本時，想要利用傳統統計檢驗方法，首先要定義模糊樣本的排序問題。利用模糊理論，說明模糊問卷調查以及模糊數的建立，并提出反模糊化轉換，以解決統計檢驗中數據排序的問題。

1.模糊數

一般地說，模糊數可分成兩大類。一類是離散型模糊數，由離散型隸屬度函數所定義；另一類是連續型模糊數，由連續型隸屬度函數所定義。連續型模糊數，依其隸屬度函數的形狀可分為：（1）實數區間模糊數；（2）三角形模糊數（Triangular fuzzy number）；（3）梯形模糊數（Trapezoidal fuzzy number）；（4）鐘形模糊數（Bell shaped fuzzy number）；（5）不對稱模糊數（Non-symmetric fuzzy number），分別由各自的隸屬度函數所定義。

三角形模糊數雖有計算簡單的優點，但梯形模糊數更接近于實際情況，也為大多數邏輯系統所接受。當考察前三者關系時，可將梯形模糊數看成是實數區間模糊數及三角模糊數的特例（梯形的上底近于0）。下面，首先定義模糊數。

定義2.1 模糊數

設U是論域，令{A1，A2…，An}為論域U的因子集，μ是一個將[0，1]映射到實數的函數，即μ：U→[0，1]。設有論域U的陳述句X，其相對于因子集隸數度函數用{μ1（X），μ2（X），...，μn（X）}表示，則陳述句X的模糊數可表示成：

當 b=c，X是三角形模糊數。

當 a=b，c=d，X是實數區間模糊數。

例 2.1 離散型模糊數的表示法

設X是某老人一天出外活動時間（小時），用模糊數表示為μn（X），論域U可看成整數論域，即出外活動時數。設U={1，2，3，4，5，6}，老人一天出外走動的時間的隸屬度函數為 {μ1（X）=0，μ2（X）=0.2，μ3（X）=0.5，μ4（X）=0.2，μ5（X）=0.1，μ6（X）=0}，則老人一天出外活動時間的模糊數可表示為

例2.2 連續型模糊數的表示法

（1）如果老人一天晚上的睡覺時間約6—8小時，可得到一組實數區間模糊數，記為[6，8]，如圖3所示。

其對應的隸屬函數關系如下：

μx（x）=1， 6≤x≤80， x<6；x>8

（2）如果老人一天的晚上睡覺時間約6小時且不少于5小時，不多于8小時，則我們可得到一組三角形模糊數（圖4），記為[5，6，8]。

（3）如果老人晚上睡覺時間通常約為5～8小時且不少于4小時，不多余10小時，則我們可得到組一梯形模糊數（圖5），記為[4，5，8，10]。

實際上，上述（1）實數區間模糊數與（2）三角形模糊數，可被看成是梯形模糊數的特例，即分別標記為[6，6，8，8]與[5，6，6，8]。

2.模糊數問卷調查表設計

在調查時，有別于傳統問卷設計的模糊問卷設計決定了抽樣的模糊數是離散型還是連續型。下面運用事例說明，如何設計與收集模糊數問卷調查的方法及技巧。

例2.3 離散型模糊數問卷調查

某個項目要調查6位老人，對生活津貼、醫療體系、休閑聯誼活動、無障礙設施、交通方便、宗教等事項所感重要性的隸屬度進行選擇，可各予以十枚硬幣，令其依心中感受的重要性將不定數量之硬幣放置各個項目上，同時必須全數用完。于是得到6組離散型模糊數的結果，如表1。

如果利用傳統問卷調查形式，也就是規定每位受訪者只能勾選一意愿最高項目，則對受訪者而言，所勾選選項應是心目中的隸數度最高者。其結果如表2。

比較以上兩種調查形式，由傳統問卷調查可知，六種選項中以醫療體系（眾數最高）最為老人所關切。利用模糊問卷調查的結果，則是交通方便（模糊眾數最高）最被關切。實際上，傳統問卷調查方式會舍棄許多信息，不如模糊問卷接近現實情況。

例3.4 連續型模糊問卷調查

連續型模糊語意量表是另一種形式的模糊問卷調查。由于其易于理解，也適用于老人議題的社會調查。比如，某個項目要調查以前從科學研究的老年人，問詢他們什么年齡段是最容易探索出成果的“黃金年齡”，這可設計如下形式的量表（圖6），請受訪者以簽字筆將最確切的“黃金年齡”部分以粗線段涂黑，隨即令受訪者在粗線段左、右分別畫上左括號、右括號表示或可稱得上“黃金年齡”。從而，得出一組梯形模糊數。

注意，當詢問的內容是類別變量時，則只可能設計為離散型模糊問卷（如例2.3）。當詢問的內容是連續尺度或序列尺度時，則可設計為離散型模糊問卷，也可設計為連續型模糊問卷（參看例3.1）。至于采取何種方式，這時要視所研究的問題或受訪者能否依指示操作而定。

3.反模糊化變換

反模糊化變換是將模糊數轉變成實數的一種方法。不論離散型模糊數（類別變量的離散型模糊數除外）還是連續型模糊數，都通過反模糊化變換轉變為反模糊化值。定義如下。

定義2.3 離散型模糊數的反模糊化值

例2.5 求離散型模糊數的反模糊化值

設X為老人一天出外走動時間（小時），其論域U={1，2，3，

4，5，6}，其隸屬度函數分別為{μ1（X）=0，μ2（X）=0.2，μ3（X）= 0.5，μ4（X）=0.2，μ5（X）=0.1，μ6（X）=0}，則老人一天出外走動時間的反模糊化值為 ：

1×0+2×0.2+3×0.5+4×0.2+5×0.1+6×0=3.2 小時

至于連續型模糊數的反模糊化變換，則考慮代表連續性的模糊集合，即代表不確定事件之一的梯形模糊集合。當獲得梯形樣本時，我們感興趣的是它在實數直線上所代表的值，即反模糊化值。在實際應用時，采取一個普遍化的非線性單位間變換，而非原始的線性單位間的變換。

當將梯形數據合理且有意義地轉化成實數時，需要確定兩件事，即變換數據必須是（1）有限維度的；（2）此類參數的相依性必需是平滑的（即可微分的）。用數學語言表示，就是此轉換群是一個李群（Lie group）。

當決定變換并實施后，要有一個新值y= f（x）取代原始梯形數據。在理想條件下，這個新量y是正態分布的。當決定如何變換時，由于可能再次變換單位，代表量x的數值變換并非唯一。

定義2.4 梯形模糊數在實數直線的反模糊化變換

3.3反模糊化轉換的一些性質

對于梯形模糊數的反模糊化變換，可將其性質歸納如下：

性質3.2 模糊數A趨近精確數，是反模糊化變換后值RA 趨近于重心cx的充分且必要條件。

性質3.3 模糊數A趨近模糊數，是反模糊化變換后值RA 趨近于重心cx + 1的充分且必要條件。

性質3.4 考慮兩梯形模糊數Ai，Aj。其重心 （cxi與cxj）距離 >1，是“重心 （cxi與cxj）的排序與反模糊化變換后值 （RAi與RAj）的排序方向不變”的充分但非必要條件。

性質3.5 考慮兩梯形模糊數Ai，Aj。其反模糊化變換后值 （RAi與RAj）距離 >1，是其反模糊化轉換后值 （RAi與RAj）的排序與重心（cxi與cxj）的排序方向不變”的充分但非必要條件。

三、中位數檢驗

1.模糊中位數

當樣本數不多或數據數有序數據或數據的測量值不穩定但大小關系仍存在時，我們可用中位數代替平均值探討總體的集中趨勢。非參數統計法經常探討具有這類特性的總體的中位數關系。當樣本為模糊數而非精確數時，可推廣傳統的中位數為模糊中位數。模糊中位數和傳統中位數相同，不會受到樣本極端值影響，因此是穩健性的集中趨勢估計量。

下面分別針對離散型與連續型兩類模糊中位數做進一步探討。連續型模糊中位數較離散型復雜，其隸數度函數常以區間均勻分布或不對稱梯形分布兩種情形表達。而區間分布可視為不對稱梯形分布的特例，本文僅對不對稱梯形分布做深入研究。

定義3.1 離散型模糊中位數

例3.1 離散型模糊中位數應用于銀發族每月基本生活費的調查

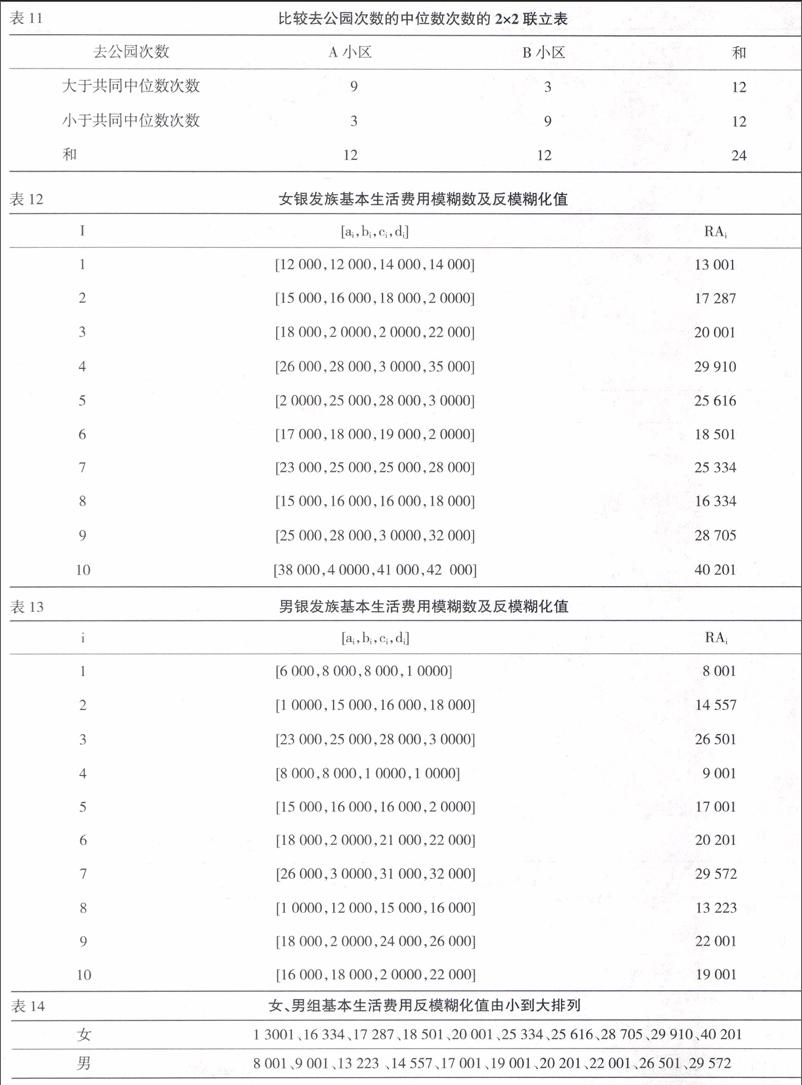
政府為老人提供多項的福利政策，比如中低收入老人生活津貼、照顧高齡老人特別照顧津貼等。考慮到最近時期市場上各種食品價格出現上漲，某個課題組想要了解老人一個月基本生活費用大致需多少錢？這個調查采用模糊中位數方式收集數據。以下是針對6位銀發老人，利用離散型模糊問卷調查表所得的關于每月基本生活費的隸屬度選擇，如表4。

由于樣本數n=6為偶數，x （3）f= 13000，x （4）f= 16000 而對應x （3）f，x （4）f的樣本值為：

注意，離散型模糊樣本的中位數仍是離散型模糊數。若利用傳統的問卷調查方式，也就是規定每位受訪者只能勾選一個意愿最高的選項，則對于受訪者而言，所勾選的選項應是心中的隸屬度最高者。其結果如表5。

從表5數據中，可以得到6位受訪者的選擇價格，依小到大排序是：8 000，10 000，10 000，15 000，20 000，25 000元或8 000，10 000，10 000，15 000，20 000，25 000元。而利用傳統中位數的取法，取出結果是10 000元。可以知道，當用傳統問卷方式進行調查，無法真正反映受訪者完整的想法。因為傳統中位數只能考慮受訪者最高意愿，所以利用模糊樣本中位數，結合模糊眾數的理論來思考，更能合理又真實地分析這類問題。

定義3.2 連續型模糊樣本中位數

設Ai=[ai，bi，ci，di]，i =1，2，…，n，是一組梯形模糊數。根據在實數直線的反模糊化值定義，計算Ai=[ai，bi，ci，di]的反模糊化值RAi，令RA （i）為將RAi排序后而得到的有序樣本值，則定義梯形模糊樣本中位數為：

例3.2連續型模糊樣本中位數應用于回味人生歲數的探討

蘇格拉底說過，“不經過反省的人生，是不值得活的。”回味是人在午夜做夢時，時常會夢到的念頭，如兒時父母的呵護、與朋友相處的時光、工作的現實和理想，在各階段的人生際遇等。下面是連續型模糊問卷調查表，是對9位受訪者“回味人生的歲數”的梯形模糊數，并依定義計算出其反模糊化值，如表6。

從表6數據中，可以得到9位受訪者對回味人生歲的數梯形模糊數的反模糊化值，由小到大的排列為16.5，18.6，32.1，

40.9，59.1，60.7，72.1，72.7，73.2。根據模糊樣本中位數定義，當 n=9時，中位數為第5位，可得模糊梯形中位數是59.1。由此可知，9位受訪者所代表的總體認為值得的回味的人生歲數約為59.1歲。

2.中位數檢驗法

當抽取元素的總體是非正態分布，其分布形式未知或樣本數少時，如采用傳統統計檢驗法，將導致過多推論，使結論變得不可信。此時可采用非參數統計方法。非參數統計經常利用中位數代表數據的集中趨勢。

非參數統計的中位數檢驗有多種方法。而由Mood所提出的中位數檢驗法，采用卡方檢驗法的統計量，可用于檢驗兩組獨立樣本來自的總體是否具有相同的中位數，應用非常廣泛。模糊數的中位數檢驗，不論是離散型還是連續型模糊數，都要使用各模糊數的反模糊化值。此檢驗方法是將兩組獨立樣本混合后，找出共同中位數，再分別算出兩組樣本大于或小于共同中位數的個別次數，制成2×2聯立表，如表7。

檢驗的假設形式為：

雙尾檢驗：H0：兩組樣本所來自的總體的中位數相等，當χ2<χ2 （α，1）H1：兩組樣本所來自的總體的中位數不相等，當χ2≥χ2 （α，1）

這個檢驗法的理論基礎是，當兩組樣本來自的總體具有相同中位數，則依共同中位數劃分的大于或小于共同中位數的實際次數，必與單純因概率所造成的大于或小于共同中位數的理論次數相去不遠。因此卡方值不應超越臨界值，所以當卡方值大于臨界值時，應拒絕H0。

例3.3 檢驗A、B兩小區的老者每周去公園次數是否相等

設有A、B兩小區鄰近公園，想要檢驗A、B兩小區的老者每周去公園次數是否相等。由A、B兩小區分別抽取13、12位老者，得各人每周去公園的次數模糊數，并計算其反模糊化值，整理成表8、9及10。

當取α=0.05，檢驗A、B兩小區老人每周去公園次數之中位數是否相等？具體方法如下：

假設為H0：兩小區每周去公園次數之中位數相等H1：兩小區每周去公園次數之中位數不相等

混合后共同中位數是5.4，整理得聯立表，如表11。

用中位數次數的聯立表（表11），計算統計量

即差異顯著，故拒絕接受H0。這表示A、B兩小區老人，每周去公園次數之中位數有可能不相等。由前例可知，此中位數檢驗法并不限制A，B兩組的樣本數必須相等。

例3.4 檢驗男、女銀發族所認為的每月基本生活費用是否相等

某個項目想要檢驗男、女銀發族所認為的每月基本生活費用是否相等，由女、男銀發族各隨機抽取10人所認為的每月基本生活費用，得其基本生活費用模糊數及反模糊化值，整理成表12、13及14。

現以α=0.05，檢驗女、男兩組銀發族老人每月基本生活費用之中位數是否相等？具體方法如下：

假設為H0：女、男兩組銀發族老人每月基本生活費用之中位數相等H1：女、男兩組銀發族老人每月基本生活費用之中位數不相等

即差異不顯著，故接受H0。這表示男、女兩組銀發族老人每月基本生活費用之中位數可能相等。

3.方差檢驗法

此檢驗法由Mood所提出，用于檢驗兩個具有相同平均水平之總體是否具有相同的方差。采用此法檢驗通常有下面幾個假設條件：

（1）兩個獨立樣本的抽取皆為隨機的。

（2）資料的尺度至少為序列尺度。

（3）兩總體除了變異程度外，其他性狀皆一致。

Mood方差檢驗法的假設形式可分為雙尾檢驗，亦可為單尾檢驗。雙尾檢驗的假設形式為：

H0：σ12=σ22即第一組之變異與第二組無不同H1： σ12≠σ22即第一組之變異與第二組不同

其中，σ不僅指總體的標準差，而泛指離散程度數。這里僅對于雙尾檢驗給出闡述，單尾檢驗的原理相同。

當求出M值后，查表得兩臨界值M'或M*。雙尾檢驗時，當M居于兩臨界值之間，即M'

這個檢驗的理論基礎是：若兩總體的變異程度不同，則由變異程度大的總體抽取的樣本，在混合排列后會趨向兩端，使等級太大或太小，并使統計量M太大或太小。所以，當檢驗統計量M大于等于大的臨界值M*或小于等于小的M'時，應拒絕H0。

例3.6 檢驗男、女老者所認為人生中“回味的人生歲數”變異度是否相等

已知某個大學教師男、女老者所認為人生中“回味的人生歲數”相等。某個項目要檢驗這所大學的男、女老者所認為人生中“回味的人生歲數”變異度是否相等，訪問19位老者（男10位，女9位）對人生中“回味的人生歲數”的看法，得到其模糊數，并計算其反模糊化值，整理成表16、17及18。

當取α=0.05，檢驗回首人生歲月中的男、女，其所認為值得回味人生的歲數，是否變異程度不同？具體方法是：

采雙尾檢驗H0：σ12=σ22即男、女組所認為‘回味的人生歲數變異度無不同H1： σ12≠σ22即男、女組所認為‘回味的人生歲數變異度不同

利用排序后的數據，表19，求其統計量M

α=0.05，n1=9、n2=10

M =（1-10）2 +（2-10）2+（3-10）2+（4-10）2+（6-10）2+（7-10）2+（9-10）2+（10-10）2+（15-10）2=281

查表得出，臨界值M'=154，M*=386，M'

這表示，回首人生回味的歲月，男、女測試結果變異程度有可能相同。由前例可知，此方差檢驗法并無不限制受檢驗的兩組樣本數必須相等。

四、結論

本文研究設計模糊數據的調查表，提出反模糊化轉換的定義，建立模糊中位數檢驗方法，對社會科學中涉及老年人有模糊特性的表述結果的模糊數據，給出了非參數統計分析，并舉例說明，得出更為準確的符合實際情況的分析和檢驗。同時，對結果進行方差檢驗，可以發現，這些信息對國家和政府制定政策及決策是十分重要的。因此，本文針對中國人口老齡化的有關信息的收集及統計分析，提出了一種有效的模糊統計分析與非參數檢驗方法，具有廣泛的應用價值和前景。

參考文獻：

[1] 王忠玉.模糊數據與統計分析[J].中國統計，2009，（9）：56-57

[2] 王忠玉，吳柏林《模糊數據統計學[M].哈爾濱：哈爾濱工業大學出版社，2008.

[3] 王忠玉，吳柏林.模糊數據均值方法及應用研究[J].統計與信息論壇.2010，（10）：13-17.

[4] 王忠玉，吳柏林.模糊數據問卷調查表的設計及應用[J].經濟研究導刊，2012，（14）：174-178.

[5] 王忠玉，吳柏林.一類模糊數據的相關系數研究[J].經濟研究導刊，2015，（2）：248-251.

[6] Klir，G..J.，Yuan，B.Fuzzy Sets，Fuzzy Logic，and Fuzzy Systems[M].NJ： World Scientic.Publishing Co.Ltd.1995.

[7] Zimmermann，H.J.，Fuzzy Set Theory and its Applications，4 edition[M].北京：世界圖書出版公司，2011.

[8] Voxman，W.Canonical Representation of Discrete Fuzzy Numbers.Fuzzy Sets and Systems，118，457-466，2001.