基于BP神經網絡的織物風格評價研究

易志建

(廣州纖維產品檢測研究院，廣東 廣州 511447)

?

基于BP神經網絡的織物風格評價研究

易志建

(廣州纖維產品檢測研究院，廣東 廣州 511447)

文章采用MATLAB7.0環境編程，充分利用人工神經網絡對非線性系統極強的模擬能力以及根據具體問題靈活處理的柔性網絡結構來構建基于BP神經網絡的織物風格評價模型。研究表明該模型對織物風格評定的可靠度和精度較好，具有一定的應用價值。

BP神經網絡；模式識別；評價模型；織物風格

1 引言

織物風格是人們憑觸覺、視覺等官能獲得的關于織物品質的評價，多數情況下以觸覺為主。長期以來，織物風格評價主要是由專家的主觀官感評價決定，雖具有權威性，但操作要求高，不易掌握。近年來，國內外對織物風格的評定方法進行了大量研究，最具代表性的是日本的川端季雄研制的織物風格測試儀。他認為織物風格是若干力學分量綜合作用的結果，只要分別測量織物的各個力學值，借助回歸法建立優化的風格值與力學量的關系模型，即可計算出織物的風格值。此外，其他一些研究者還根據織物力學指標的作用程度，利用模糊聚類法、系統聚類法等對織物的風格進行鑒別和分類。這些研究集中探討了織物的力學指標與織物風格之間的關系，即建立織物基本風格與力學指標間的數學模型。然而，服裝面料風格的評價是一個帶有消費者主觀意識的產物，不同的消費群體、消費領域，對織物風格的要求是不同，因而這些模型在實際應用中都存在某些缺陷[1]。

人工神經網絡是近年來國內外正在研究的一種熱點技術。由于神經網絡具有自學習、容錯性、分類能力強和并行處理等特點，可以不斷挖掘出研究對象之間內在關系，以實現最終問題的求解。因此，本文基于BP神經網絡對織物風格進行了分析和評價研究。

2 BP神經網絡概述

BP神經網絡，即誤差反向傳播神經網絡，是神經網絡模型中應用最廣泛的一種[2-3]。它由輸入層、隱含層和輸出層構成。假設BP神經網絡每層有N個節點，作用函數為非線性的Sigmoid型函數，一般采用f(x)=1/(1+e-x)，學習集包括M個樣本模式(Xp，Yp)。對第P個學習樣本(P=1，2，…，M)，節點j的輸總和記為netpj，輸出記為Opj，則：

(1)

如果任意設置網絡初始權值，那么對每個輸入樣本P，網絡輸出與期望輸出(dpj)間的誤差為：

(2)

BP網絡的權值修正公式為：

Wji=Wji(t)+η δpjOpj

(3)

(4)

上式中引入學習速率η，是為了加快網絡的收斂速度。通常權值修正公式中還需加一個慣性參數a，從而有：

Wkj=Wkj(t)+ηδpjOpj+a(Wkj(t)-Wji(t-1))

(5)

式中，a為一常數項,它決定上一次的權值對本次權值的影響。其具體算法步驟詳見文獻[4]。

3 織物風格評價模型的建立與訓練

3.1 樣本數據的選擇

現有的研究結果表明，織物風格由織物本身的物理、力學性能所確定，這些性能主要包括織物的抗彎特性、摩擦特性、壓縮特性及表面特性等。而中厚織物的基本風格有硬挺度、豐滿度和光滑度。被測樣品的工藝參數均不相同，有15名專家進行了主觀評定，主觀評定由10個等級描述。樣本數據[5]見表1、表2，其中表1作為網絡的輸入信號，表2作為網絡的目標輸出。

表1 網絡的輸入信號

3.2 建立BP神經網絡模型

①首先確立網絡的結構，設置合理的網絡參數(如學習速率)，進行網絡權值及閾值初始化。采用3層BP神經網絡：第一層是輸入層，輸入表1中1～12號共12個樣本，每個樣本有10個相關因素，分別是活絡率、彎曲剛性、靜摩擦因數、動摩擦因數、穩定厚度、壓縮彈性率、比壓縮彈性率、蓬松度、起拱殘留率、面密度因此輸入層設定10個神經元；第二層是隱含層，隱含層神經元節點數是根據網絡模型訓練時所產生的誤差大小而確定的。第三層是輸出層，由于輸出參數有硬挺度、豐滿度和光滑度，因此輸出層設3個神經元節點。

②確定模型所需的訓練樣本，對每個樣本重復步驟③～⑥。

③計算網絡的實際輸出。

每個神經元上作用的函數常用Sigmoid型非線性函數：

f(x)=1/(1+e-x)

(6)

(7)

Ok=f(netk)

(8)

其中，為從神經元Uk到上一層的神經元Uj的連接權重值；Oj為神經元Uj的輸出，netk為神經元Uk的輸入值；Ok為Uk神經元的輸出；θk為神經元Uk的閾值。由式(7)和式(8)計算神經元Uk的輸入值和輸出值。中間隱含層和輸出層的神經元的輸入/輸出也采用這種計算方法。

④計算網絡的反向誤差。若樣本容量是k，n是輸出節點個數(在此n=1)，網絡的收斂目標是網絡輸出層的輸出值與實際值的總誤差最小。

(9)

⑤權重學習，修改各層的權重值和閥值。

當誤差不滿足精度要求時，將方差對權重偏導，按梯度下降法修正層間權重值，不斷迭代，致使直到滿足精度E趨向0為止。權值的調整按下述方法進行，其中，η為學習速率。

Δωij=-η?E/?ωij=η δiOi

(10)

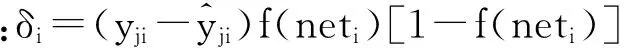
(11)

(12)

式(12)中，為所有與隱含層的神經元相連的輸出層神經元Wli的反傳誤差，于是權值的修正公式為：

ωij=ωij-Δωij=ωij-η δiOi

(13)

若滿足精度要求，可對織物風格評定，否則轉向②。

這里神經網絡模型采用DPS數據處理系統的BP神經網絡模型實現的有指導下的訓練，即以15組數據作為直接訓練數據，6組數據作為訓練檢驗和驗證數據。學習算法采用動量法，學習率采用自適應調整算法。進入BP神經網絡訓練時，可按網絡結構確定網絡參數，這里輸入層設定10個神經元，隱含層l層，隱含層神經元節點數為20，Sigmoid參數為0.9，允許誤差0.0001，最大訓練次數2000，并對輸入節點的數值進行標準化轉換。

反復訓練調整網絡參數后確定該模型采用LvenbergMarquardt算法，訓練函數為trainlm。該網絡的隱含層節點采用logsig作為傳遞函數，輸出層節點采用purelin作為傳遞函數[6]。

圖1為網絡訓練過程的誤差變化曲線圖。實驗中發現，模擬復雜程度不高的非線性關系采用這種網絡結構可以達到比較好的效果，在訓練9次后精度已達到10-4，該網絡模型能滿足預設精度，訓練成功。

4 網絡模型預測結果與分析

BP網絡運行多次后(這里隱含層神經元個數取12)，樣本誤差為0.0001。學習訓練樣本組(1#～10#)的擬合值與專家評定值如圖2所示，無學習訓練的BP網絡輸出的擬合值與專家評定值如圖3所示，根據BP神經網絡對檢驗和驗證組(10#～15#)進行的預測的結果與專家評定值的比較如圖4、圖5、圖6所示。

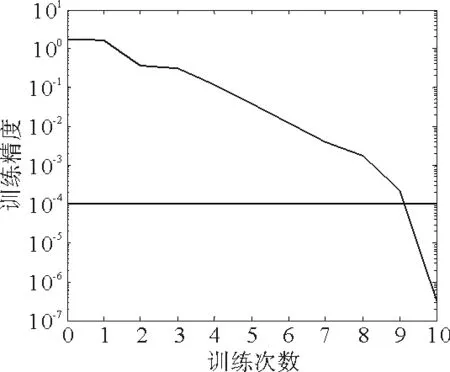
圖1 網絡訓練過程的誤差變化曲線圖

圖2 訓練后的BP網絡模型輸出擬合曲線

圖3 未經訓練的BP網絡模型輸出擬合曲線

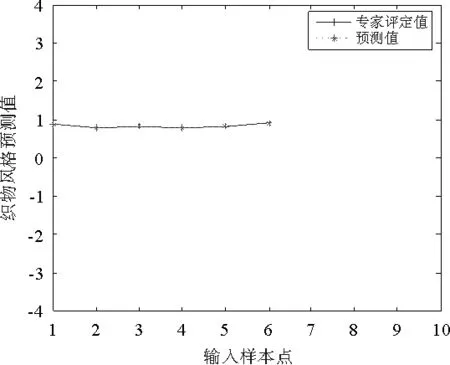
圖4 BP網絡模型輸出硬挺度預測曲線

預測結果表明：系統通過學習樣本的學習具備了一定的聯想識別能力，可以正確識別陌生樣本，不僅對學習樣本的擬合程度高，而且6個檢驗和驗證樣本的預測結果與專家評定值非常接近(見表3)。隨著更多試驗數據的積累和網絡的不斷訓練，會進一步減少網絡訓練時的振蕩，使預測結果波動范圍不斷減小。

圖5 BP網絡模型輸出豐滿度預測曲線

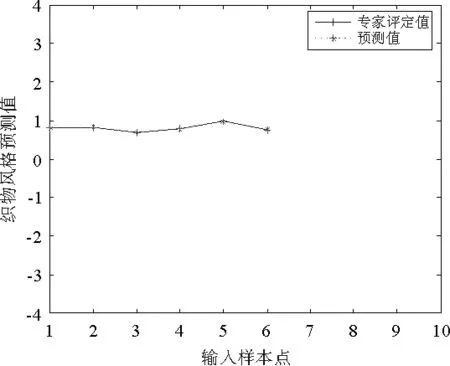
圖6 BP網絡模型輸出光滑度預測曲線

樣本硬挺度專家預測豐滿度專家預測光滑度專家預測10.890.86980.840.83650.800.802020.790.79060.700.69960.800.821430.830.82990.790.78910.690.694040.790.79040.890.88030.790.786450.840.84070.730.72350.970.969960.890.88990.830.83090.760.7664

5 結語

5.1 BP神經網絡有對非線性系統很強的模擬能力，具有可根據具體問題靈活處理的柔性網絡結構，可將一組樣本的輸人輸出問題變為一個非線形優化問題。經過多次訓練后，網絡具有極強的逼近能力。

5.2 BP神經網絡模型的自適應和自組織能力，對織物風格主觀評定的尺度，具有較強的適應性，通過對不同樣本集的訓練，可以適應特定條件下的模式識別[7]，從而在一定程度上彌補了以往風格評定模型中的一些缺陷。

[1] 洪志貴．織物風格評價的研究[J]．紡織學報.1993，14(4)：160—163.

[2] 張立明.人工神經網絡的模型及其應用[M].上海：復旦大學出版社, 1995.

[3] 焦李成.神經網絡系統理論[M].西安：西安電子科技大學出版社，1990.

[4] Kandel E R，Schwarts J. Principles of Neural Science[M].Elsevier，1985.

[5] 曹安照.RBF神經網絡在織物風格評價中的應用[J].紡織學報，2005，26(6)：27—3.

[6] 從爽．面向Matlab工具箱的神經網絡理論與應用[M].合肥：中國科學技術大學出版社，1998．

[7] 嚴灝景，潘寧.織物風格的客觀評價的模式識別方法[J].紡織學報，1984，6(12)：27—3.

Researches on Fabric Handle Assessment Based on BP Neural Networks

YiZhijian

(Guangzhou Fiber Product Testing and Research Institute, Guangzhou 511447, China)

The paper set up a fabric handle assessment model based on BP neural networks. It took full advantage of artificial neural network’s powerful simulative function and capacity of flexible network structure to deal with issue flexibly. Research shows that with good reliability and precision, the model has certain application value.

BP neural network; process parameter; forecasting model; fabric style

2017-03-14

易志建(1987—)，男，廣東佛山人，助理工程師。

TS101.1

A

1009-3028(2017)03-0036-04