渤海常見土類剪切波速與埋深關系分析1

榮棉水 呂悅軍 蔣其峰 修立偉

?

渤海常見土類剪切波速與埋深關系分析1

榮棉水1）呂悅軍1）蔣其峰2）修立偉1）

1）中國地震局地殼應力研究所，北京 100085 2）山東省地震局，濟南 250014

土層的剪切波速是巖土地震工程中重要的物理量，本文利用多年來在渤海海域地震安全性評價中積累的資料，研究了渤海常見土類剪切波速和埋深的關系。利用非線性最小二乘法，采用指數函數、一次函數、二次函數、冪函數、“冪函數+常數函數”、“冪函數+一次函數”6種回歸模型對各類土的剪切波速和埋深的關系進行了回歸分析，以擬合優度以及最小二乘擬合的誤差平方和為評價指標對比了各種模型擬合效果的優劣。結果表明，“冪函數+一次函數”回歸模型的擬合效果最好。此外，本文給出了該海域常見的7類土在此回歸模型下的擬合公式的系數，以供工程中參考。

渤海 剪切波速 埋深 回歸分析 擬合

引言

土層的剪切波速在巖土地震工程中有廣泛的應用（劉紅帥等，2010）。地震工程中，土層剪切波速是確定場地類別、場地地震反應分析、計算動力學參數的重要參數。在工程實踐中，土層剪切波速缺失的情況時有發生，這就需要依據經驗公式對剪切波速進行科學合理的計算，如何確定合理的經驗公式就成為重要的課題。土層的剪切波速與很多參數有關，包括土的成分、結構、類別、密度、埋深等（Hardin等，1972），而研究表明，在某個區域范圍內，土層的剪切波速與埋深有很強的相關性，這就為計算剪切波速提供了經驗性的手段。曾有不少學者研究過不同地區土體的剪切波速與埋深的經驗關系，如周錫元等（1990）對沿海城市地區、程祖鋒等（1997）對深圳地區、高玉峰等（2003）對合肥地區、戰吉艷等（2009）對蘇州城區、蘇旭等（2009）對西寧市、邱志剛等（2011）對黑龍江地區、齊鑫等（2012）對下遼河平原、趙淑芳等（2012）對昆明呈貢新區均開展了相關的研究。這些研究表明，不同地區由于土體沉積歷史等因素的不同，導致擬合經驗公式系數存在很大差異。此外，在剪切波速與埋深的函數關系方面，統計分析過的學者存在不同的認識。如Lew等（1981）曾指出剪切波速與埋深之間呈冪函數關系；周錫元等（1990）給出的沿海城市場地土剪切波速與埋深呈冪函數形式；蘇旭等（2009）擬合西寧市剪切波速與埋深的關系時也采用了冪函數形式；戰吉艷等（2009）對蘇州城區深軟場地土的統計采用了線性函數、冪函數分段形式；劉紅帥等（2010）曾研究了淤泥質土、碎石土、砂土、粉土、黏性土剪切波速和埋深的關系，認為除淤泥質土外，其他常規土類剪切波速與埋深間的關系用一元二次多項式擬合精度最高；邱志剛等（2011）、齊鑫等（2012）的工作中則采用了包括線性模型、冪函數模型、一元二次多項式模型在內的多種模型；狄圣杰等（2014）則曾用廣義回歸神經網絡預測的方法對剪切波速與埋深的關系進行了探討。綜合以上研究可知，區域土體剪切波速與埋深的經驗函數關系并沒有一個普遍公認的函數形式，何種函數更為接近實測結果仍值得研究，其結果可能也與所研究的區域有關。渤海蘊藏著豐富的油氣資源，隨著對資源進行開發利用，渤海中建設了一系列的海洋工程項目，按照《建筑工程抗震設防分類標準》，這些工程建筑需要重點設防。在過去的10年中，渤海海域開展了大量的工程建設，如跨海橋梁、隧道、海洋平臺等蓬勃開展，積累了豐富的土層剪切波速資料，具備了研究剪切波速與埋深關系的基礎。本文在前人研究成果的基礎上將嘗試構造新的回歸模型，對比篩選出最優的回歸模型并給出相應的系數。

1　渤海地質地貌概況

渤海是一個近封閉的內海，為陸架淺海盆地，由遼東灣、渤海灣、萊州灣、渤海中央盆地以及渤海海峽5部分組成。渤海周圍有黃河、海河、遼河、灤河等含沙量很大的河流流入，使得渤海水深較淺、地形平緩，海底從萊州灣、渤海灣和遼東灣3個海灣向渤中盆地及渤海海峽傾斜，坡度平緩，平均坡度0.13‰，渤海水深較淺，平均水深18m（陳義蘭等，2013）。渤海位于新華夏構造第二沉降帶內，是營口隆起、華北凹陷、魯西隆起與郯廬斷裂帶的交匯區。渤海分布有厚層第四紀沉積物，在渤中盆地中，第四紀的沉積厚度約600m以上，在渤海灣西岸第四紀的厚度約300m。在更新世期間，渤海曾發生過若干次海進和海退，所以渤海地區更新世地層中海相地層和陸相地層交替出現。在10萬年以來的地層中，共發現有3次海侵事件，從下而上分別稱為滄州海侵、獻縣海侵、黃驊海侵。全新世沉積伴隨著玉木冰期的最盛時期結束后的全新世海侵形成，在渤中盆地一般厚約8—13m，在遼東灣西側，其厚度較淺，約2—4m，在渤海西岸一般厚12—14m，表現為灰色—暗灰色沉積層，在黃河和海河口附近海域，受近岸物質的影響，一般表現為黃色沉積層（中國科學院海洋研究所海洋地質研究室，1985）。

2　數據來源

本文所用土層剪切波速和埋深數據來自于中國地震局在渤海海域工程地震安全性評價中近十余年來積累的資料，這些資料涵蓋了渤海海域錦州、渤中、南堡、錦西、遼東、秦皇島、墾利、遼東、岐口等油田33處場地的鉆孔剪切波速資料，取樣鉆孔的分布如圖1。這些海域鉆孔一般深約120m，鉆孔土類以細粒土類為主，包括粉質粘土、粉質細砂、粉砂、粉土、砂質粉土、細砂，其中粉質粘土和粉質細砂分布最廣。剪切波速均為獲取土樣后在實驗室測得，埋深為取樣位置的深度，資料的可靠性很強。對資料進行統計后，按照土類的不同，對數據進行了分類匯總。根據離散點的趨勢對個別異常數據進行了剔除，數據仍余500多組。所統計的土類為渤海常見土類，包括粉質粘土、砂質粉砂、粉砂、粉質細砂、細砂、砂質粉土、粉土共7類。

3　剪切波速測量方法

剪切波速測量裝置由三軸壓力室、剪切波發射與接收傳感器以及DB4型超聲測量儀組成，如圖2。具體測量過程是：①制備直徑3.91cm、高8.0cm的原狀土樣，套上橡皮膜后安裝進三軸壓力室內；②根據土樣所在土層的上覆有效壓力，給土樣施加等向固結壓力（即圖2中圍壓3與軸向應力1相等），使土樣排水固結；③待其固結后，對土樣輸入剪切波，利用儀器測量出剪切波通過土樣的旅行時；④土樣的高度除以旅行時即得到土樣的剪切波速。

4　數據處理

剪切波速有隨深度的增加而增大的規律，不同的學者對不同地區的研究不盡相同，現在已有的經驗公式的形式有指數函數、一次函數、二次函數、冪函數、“冪函數+常數函數”（胡鈞等，1997）。其回歸模型具體如下：

（1）指數函數模型：=e；

（2）一次函數模型：=+；

（3）二次函數模型：=2++；

（4）冪函數模型：=ah；

（5）“冪函數+常數函數”模型：=ah+；

其中，、、為擬合系數，為土體埋深。作者首先按土類分類統計了渤海常見土類的剪切波速和相應的埋深，然后分別用上述5種回歸模型對剪切波速和埋深間的關系進行回歸分析，并計算相應的擬合優度和最小二乘法擬合的誤差平方和，其結果示于表1。擬合優度是用來度量變量在多大程度上能夠被所估計的回歸方程所解釋的指標。對于一組樣本觀測值（X，Y），=1，2，…，，若得到以下樣本回歸線，以一次函數舉例：

則的第個觀測值與樣本均值的離差，可分解為2個部分：

形式，則ESS、RSS和交叉項的值會發生變化。已有文獻研究（徐秦等，1992）證實，若擬合曲線為線性函數形式，如式（1）或回歸模型（2）等，交叉項為零。若擬合曲線為非線性函數，則交叉項為正、負或零均有可能。一般情況下，若實際觀測點離樣本回歸線越近，則ESS在TSS中所占比重越大，RSS在TSS中占比越小。本文將擬合優度2定義如下：

2=1-RSS/TSS （4）

這一擬合優度定義主要出于以下幾點考慮：①線性與非線性曲線通用的擬合優度指標雖引起了一些學者（徐秦等，1992；張世強，2002）的注意，但簡單、合理適用的指標仍在討論過程中；②解決實際問題時，所擬合的回歸曲線優劣標準為，在相同參數個數條件下，擬 合值越接近觀測值，則認為擬合得越好。若把{Y}與{}視為維空間中的點，若{Y}與{}距離越小，則可認為用{}估計{Y}越好。式（4）中RSS則恰好表示維空間中{Y}與{} 的距離，具有清晰的幾何意義。RSS/TSS則體現了相對誤差的概念。文獻（張世強，2002） 中將RNL=1-做為線性與非線性曲線通用的擬合優度指標，但作者認為，這一定 義與式（4）并無本質區別；③在線性回歸中，式（4）即為統計學中常用的可決系數；④RSS主要表示回歸線不能解釋的部分，ESS與交叉項均與回歸線能解釋的部分有關，則式（4）可以看做總體平方和之中，與回歸線能解釋的部分有關的成分所占的比例。

在式（3）中交叉項大于或等于零的情況下，2（此時其范圍為0—1）越接近1，說明實際觀測點離樣本越近，擬合優度越高。此外，本文回歸到用最小二乘法確定擬合函數中各個系數時采用觀測值與擬合值誤差平方和最小的原則上來，也計算了每一個2相應的RSS值，作為評價擬合效果的另一個指標。回歸模型（1）—（5）的擬合結果分別示于圖3—圖9中，表示擬合效果的數值列于表1。表1中的數值表明，在擬合參數個數相同的情況下，冪函數擬合效果最佳。此外，從圖中不難發現，當埋深較淺時，如<20m時，剪切波速隨埋深的變化呈現冪函數變化特征；當埋深較大時，如>40m時，剪切波速隨埋深變化更接近一次函數特征。因此，在前人研究的基礎上，作者綜合冪函數與一次函數的特點，構造了新的“冪函數+一次函數”的表達式形式，以期獲得更好的擬合效果。函數模型如下：

（6）“冪函數+一次函數”模型：=ah++其中，、、、為擬合系數，為土體埋深。本文選用Matlab繪制統計數據的散點圖，并利用fit函數的非線性最小二乘法擬合功能對數據進行擬合，計算出回歸曲線的系數、擬合優度2、誤差平方和，最后，對比各回歸模型的擬合優度，并給出最優的回歸模型的系數，以供工程中參考。

5　數據處理結果與分析

經過程序處理和計算，得到了7類土分別在6種回歸模型下的剪切波速-埋深的表達式，以及相應的擬合優度、誤差平方和（表1）。從表中看出，從模型（1）至模型（6），擬合優度越來越接近1，同時誤差平方和逐漸減小，表明從模型（1）至模型（6）擬合效果越來越好，而模型（6）的擬合效果最好。筆者也曾嘗試4參數的三次函數或更高次函數形式的擬合，難以獲得較好擬合效果。綜合以上擬合結果可知本文構造的“冪函數+一次函數”的回歸模型具有很好的適用性。為直觀地對比回歸結果的優劣，本文給出粉質粘土、粉質細砂等7類常見土類在回歸模型（1）—（6）下的擬合結果（圖3—圖9）。可以看出模型（1）至模型（3）對埋深較淺的土樣的剪切波速擬合效果不理想，模型（4）對埋深較淺的土樣的剪切波速的擬合效果很好，而埋深較大時擬合效果不佳，在這一方面，模型（5）、模型（6）依次有了更進一步的改進，模型（6）對試驗數據具有最佳的擬合效果。渤海海域各類土在模型（6）下的各項系數見表2。

表1　各類土在各回歸模型下的擬合優度

續表

注：2表示擬合優度，RSS表示誤差平方和，其單位為m2/s2。

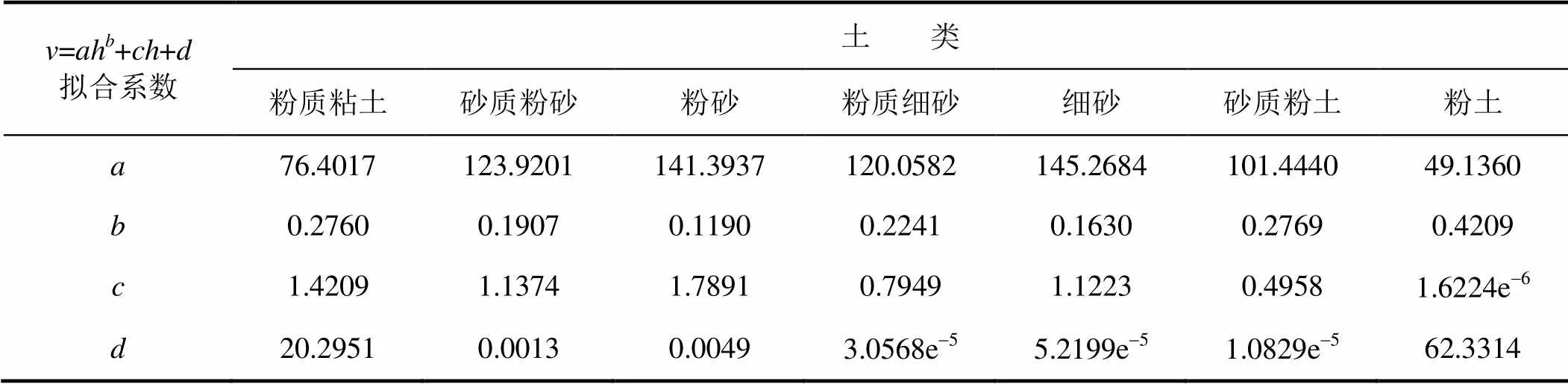
表2　各土類采用v=ahb+ch+d形式擬合的系數

6　結論

本文統計了渤海海域常見土類的剪切波速和埋深數據，研究了剪切波速與埋深之間的經驗關系，構造了“冪函數+一次函數”形式的回歸模型。通過與其他形式的回歸模型擬合優度及誤差平方和的對比，證實該回歸模型具有很好的適用性。此外，本文給出了渤海各常見土類在該回歸模型下的系數。本文的工作可為海域工程中缺失剪切波速數據的場地提供了重要的參考依據，也為鉆至一定深度后終孔并推測下方土層剪切波速提供了有效的推測手段。

致謝：感謝匿名審稿專家提出的中肯的修改意見和建議。本文的基礎數據多引用自筆者參與和收集的所在單位的多項海域建設項目工程場地地震安全性評價報告，作者向參與這些海域項目的技術人員表示感謝，如有引用不當之處還請諒解。

陳義蘭，吳永亭，劉曉瑜等，2013．渤海海底地形特征．海洋科學進展，31（1）：75—82．

程祖鋒，李萍，李燕等，1997．深圳地區部分巖土類型剪切波速與深度的關系分析．工程地質學報，5（2）：163—168．

狄圣杰，汪明元，張昆等，2014．江蘇近海地層原位剪切波速相關特性及預測方法研究．海洋學報，36（3）：127—133．

高玉峰，劉漢龍，2003．合肥膨脹土剪切波速的特征分析．巖土工程學報，25（3）：371—373．

胡鈞，杜堅，1997．上海場地土的脈動特性及剪切波速特征．物探與化探，21（4）：305—307，299．

劉紅帥，鄭桐，齊文浩等，2010．常規土類剪切波速與埋深的關系分析．巖土工程學報，32（7）：1142—1149．

齊鑫，丁浩，2012．下遼河平原區剪切波速與土層埋深關系分析．世界地震工程，28（3）：151—156．

邱志剛，薄景山，羅奇峰，2011．土壤剪切波速與埋深關系的統計分析．世界地震工程，27（3）：81—88．

蘇旭，楊麗萍，鄒海寧，2009．西寧市區土層剪切波速隨深度變化特征．高原地震，21（1）：12—16．

徐秦，薛茜，徐睿，1992．淺論曲線擬合中的相關指數2．中國衛生統計，9（6）：44—45．

戰吉艷，陳國興，劉建達，2009．蘇州城區深軟場地土剪切波速與土層深度的經驗關系．世界地震工程，25（2）：11—17．

張世強，2002．曲線回歸的擬合優度指標的探討．中國衛生統計，19（1）：9—11．

趙淑芳，楊宏亮，2012．場地剪切波速的特征分析．云南大學學報（自然科學版），34（S2）：267—271．

中國科學院海洋研究所海洋地質研究室，1985．渤海地質．北京：科學出版社，1—11．

周錫元，王廣軍，蘇經宇，1990．場地·地基·設計地震．北京：地震出版社，28—172．

Hardin B. O., Drnevich V. P., 1972. Shear modulus and damping in soils: design equations and curves. Journal of Soil Mechanics & Foundations Division, 98(7): 667—692.

Lew M., Chieruzzi R., Campbell K. W., et al, 1981. Correlations of seismic velocity with depth. In: Proceedings of the 1st International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics (ICRA GEESD) U.S.A. St. Louis, Missouri, 1981. University of Missouri—Rolla.

Relationship between Shear Wave Velocity and Depth for Conventional Soils in the Bohai Sea Area

Rong Mianshui1), Lv Yuejun1), Jiang Qifeng2)and Xiu Liwei1)

1) Institute of Crustal Dynamics, China Earthquake Administration, Beijing 100085, China 2) Earthquake Administration of Shandong Province, Ji'nan 250014, China

Shear wave velocity of soil layers is an important physical index in geotechnical earthquake engineering. Based on the experimental data accumulated over the years in the seismic safety evaluation research projects of the Bohai sea area, relationship between shear wave velocity and depth of conventional soils has been studied. In order to achieve the best fitting of experimental data, 6 regression models including exponential function, linear function, quadratic function, power function, power function combined with constant function, power function combined with linear function, have been used for regression analysis through nonlinear least square fitting method. The goodness-of-fit has been used as an index to evaluate the matching effect. The results showed that, the proposed form of function which combining power function with linear function has the best matching effect for experimental velocity data. Furthermore, the fitting coefficients of proposed function for 7 kinds of conventional soils in the Bohai Sea area have been presented for reference in engineering.

The Bohai Sea; Shear wave velocity; Depth; Regression analysis; Fitting

1基金項目 中央公益型院所基本業務專項項目資助（ZDJ2014-07、ZDJ2015-02）

2015-12-19

榮棉水，男，生于1982年。博士，高工，碩士生導師。主要從事場地地震反應分析、強震動觀測等方面的研究。E-mail：waltrong@126.com

榮棉水，呂悅軍，蔣其峰，修立偉，2017．渤海常見土類剪切波速與埋深關系分析．震災防御技術，12（2）：288—297． doi：10.11899/zzfy20170205