軋機主傳動系統及帶材耦合振動有限元分析

郭瀟檣，杜國君，李 博

(1.燕山大學建筑工程與力學學院，河北 秦皇島 066004；2.燕山大學建筑工程與力學學院，河北 秦皇島 066004；3.西安現代控制技術研究所，陜西 西安 710065)

軋機主傳動系統及帶材耦合振動有限元分析

郭瀟檣1，杜國君2，李 博3

(1.燕山大學建筑工程與力學學院，河北 秦皇島 066004；2.燕山大學建筑工程與力學學院，河北 秦皇島 066004；3.西安現代控制技術研究所，陜西 西安 710065)

介紹了ANSYS有限元軟件的基本原理以及所使用的SOLID186結構單元的特性，通過ANSYS有限元軟件定義耦振模型相關參數，根據圖紙尺寸建立某軋機主傳動系統及帶材結構模型。并對所建模型進行模態分析，得出軋機主傳動系統及帶材結構模型的固有頻率以及所對應的振型。然后進行諧響應分析，得到諧響應分析結果。最后綜合模態分析和諧響應分析結果，證明了主傳動系統及帶材模型在簡諧載荷頻率為8.4 Hz時，系統結構發生共振。為同類軋機設計和實際生產提供了參考依據。

軋機；有限元分析；扭振；耦合振動

0 前言

我國正處于經濟高速發展階段，因此市場需求量非常龐大，鋼鐵行業是決定國民經濟增長的基礎行業。國內某些企業進口的軋機，因振動問題，降速至設計速度的60%進行生產，軋機故障問題嚴重影響著生產的有序進行[1,2]。由軋機振動引起的故障輕則降低生產效率，影響產品質量；振動過于劇烈，甚至會引發事故，停產整修[3-5]。所以研究軋機主傳動系統振動非常必要。

1 軋機主傳動系統的有限元研究

有限單元法可以用來求解各種工程問題，需要用到電子計算機來進行計算。結構分析中的各種問題，如靜力學、動力學、模態分析、諧響應分析等都可以用ANSYS軟件進行求解計算[6,7]。

本文使用ANSYS有限元軟件對軋機主傳動系統以及帶材進行模態分析以及諧響應分析。ANSYS有限元分析的總體思路是將連續的模型離散化，分別求解后再將結果進行整合。具體步驟為：前處理階段將軋機主傳動系統以及帶材整體進行建模，對所建模型進行網格劃分、施加邊界條件，選擇分析類型，然后進行求解，最后對所得結果進行后處理[8]。

建模前需要定義結構類型，ANSYS有限元軟件中單元有七大類一百多種，本文使用的是結構分析單元中的SOLID186結構實體單元。該單元為高階3D 20節點實體單元，即該單元定義有20個節點，每個節點定義3各自由度，即x、y和z方向的平動自由度，無轉動自由度。并且SOLID186結構單元可以退化為四面體單元、五面體單元、金字塔單元、五面體棱柱單元等[9]，如圖1所示。

圖1 SOLID186結構單元

ANSYS有限元動力學分析中，網格劃分是非常重要的一個環節，網格劃分的好壞直接決定計算精度以及計算速度。網格劃分的基本原則[10]為：

(1)對于某個具體模型，大致可以估計出哪些位置是應力集中區域，例如過渡尖銳的尖角、截面積突變的位置等，應盡量使得網格劃分較為密集一些，這樣可以使計算結果有足夠的精度；

(2)在精度足夠滿足工程應用的前提下，并不是網格劃分越密集越好，雖然現今的微型計算機性能相比于十幾年前已經有了質的飛躍，但是考慮到計算時間以及存儲空間等時間成本及資源占用上，在滿足計算精度的要求下，網格劃分應盡可能地越稀疏越好。綜上所述，網格劃分應該在保證足夠精度與減少時間成本的矛盾上達到很好的折衷。

2 建立模型

首先定義所需的計算參數及主要尺寸。參數如下[11]

彈性模量E20.6 GPa

泊松比γ0.3

密度p7850 kg/m3

軋輥有效長度 1.58 m

軋輥有效直徑 0.825 m

聯結器長度 3.23 m

本文按照某廠提供的圖紙[12]，對某軋機主傳動系統及帶材，按圖紙中的實際尺寸進行建模。為使建模簡化并且減少網格劃分數量以及隨后計算所需的時間，略去系統結構中對于計算精度的影響可以忽略不計的部分。圖2所示為F2機架主傳動系統結構模型。圖3所示為主傳動系統及帶材結構模型。

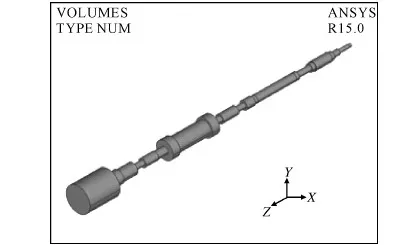
圖2 F2機架主傳動系統結構模型

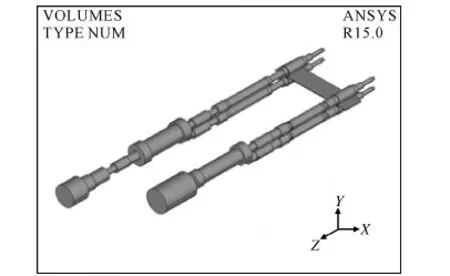
圖3 主傳動系統及帶材結構模型

圖3中可以看到，F2、F3機架上下輥之間由帶材相連接，該模型尺寸較大，經過多次計算，使用Smartsize 9劃分，精度已經可以達到要求。

3 ANSYS有限元模態分析

本文使用SOLID186結構單元，并用Smartsize 9進行自動網格劃分。網格劃分后的模型如圖4所示。按實際情況，對各軸承處施加旋轉約束，系統會求出各種振動形式的頻率，如橫向、軸向和扭轉振動等，只需篩選出扭振振型。

圖4 網格劃分后的結構模型

4 模態分析結果討論

在分析類型(Analysis Type)中選擇使用Block lanczos模態分析法。該模態分析法的特點是計算速度快，可以用于大多數情況下。而且Block lanczos模態分析法可以在任何命令下自動使用稀疏矩陣方程進行求解。在計算系統的固有頻率時，該方法可高效提取系統模態，在實體單元模型中應用廣泛[13]。

從圖5中可以看出，一階固有頻率為24.387 Hz，在聯結器處應變較大，該處為薄弱環節。二階固有頻率為52.861 Hz，軋輥軋制面應變較大。

從圖6中可以看出，主傳動系統及帶材的一階固有頻率為8.439 Hz。由于帶材的連接，使得各機架間的傳動系統彼此相連，不再是孤立的。帶材的作用使主傳動系統結構的固有頻率明顯降低，從24.387 Hz將為8.439 Hz。而且應變最大區也由聯結器處變為電機端處。

圖5 主傳動系統一階、二階固有頻率所對應的振型

圖6 主傳動系統及帶材一階固有頻率所對應的振型

由圖7可知， 對于主傳動系統及帶材模型的二階固有頻率的振型變化情況與一階變化情況基本相同，不再做深入討論。由此可見，主傳動系統和帶材之間的相互影響非常重要，在研究軋機結構的動力學問題時，應全面綜合的考慮各部件的影響，才能更客觀有效的對實際工程以及設計研究提供準確參考。

圖7 主傳動系統及帶材二階固有頻率所對應的振型

5 諧響應分析及其結果討論

對主傳動系統及帶材模型做諧響應分析。在帶材的橫截面處施加均布拉力，定義分析類型為Harmonic分析，頻率范圍為6～10 Hz，子步為10[14]。經過計算，選取計算結果中頻率為8.4 Hz，振型如圖8所示。

圖8 諧響應分析載荷頻率為8.4 Hz時振型圖

從圖8中可以看出，該載荷頻率與主傳動系統及帶材模型一階固有頻率8.439 Hz非常接近，并且應變云圖也非常相似。因此，選取聯結器左端處和電機端的節點，查看該處UX及UY響應幅值隨時間變化的曲線，如圖9、圖10所示。

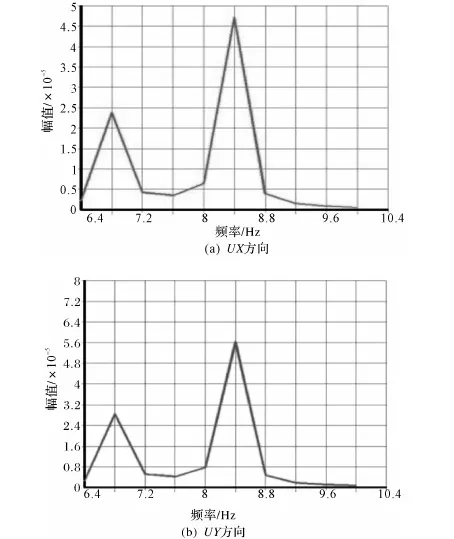
圖9 聯結器左端處響應振幅隨頻率變化曲線

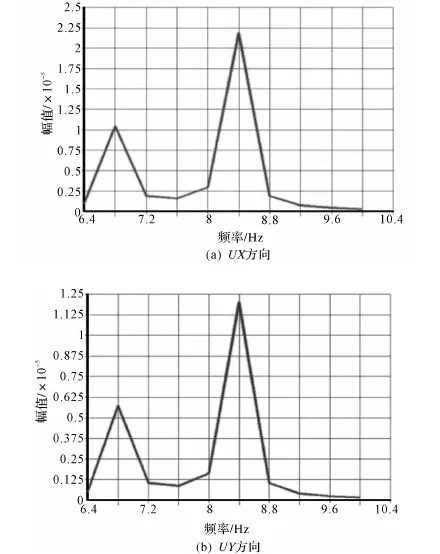
圖10 電機端響應振幅隨頻率變化曲線

從圖9可知，在聯結器左端所選取的節點處，隨著掃頻由6.4～10 Hz，無論是UX幅值曲線還是UY幅值曲線，都經歷兩個峰值，在頻率值為8.4時幅值達到最大值，分別為UX=4.7×10-5和UY=5.6×10-5，即當載荷頻率為8.4 Hz時主傳動系統及帶材模型在該處發生共振。

從圖10中可以看出，電機端所選取的節點處，與聯結器所選取的節點相類似，也是在頻率值為8.4 Hz時發生共振，幅值分別為UX=2.24×10-5和UY=1.21×10-4。

6 結論

對某軋機主傳動系統(包含帶材)模態分析結果表明，扭振一階固有頻率為8.439 Hz。聯結器兩端、電機端為薄弱環節，比較符合生產過程中聯結器或十字頭處容易發生破壞的情況。所以設計軋機時應著重對于以上薄弱環節進行更好的強度設計。

由主傳動系統及帶材結構的諧響應分析可知。對于一階固有頻率，未能精確掃過模態分析所得出的頻率值，但是在非常接近的范圍已經得出比較滿意的結果，即主傳動系統及帶材模型在簡諧載荷頻率為8.4 Hz時，聯結器的薄弱點處和電機端UX和UY幅值響應隨頻率變化曲線均出現峰值，證明系統結構發生共振，該分析可對軋機設計或生產實際提供一定參考價值。

[1] 趙麗娟，高丹.國內外冷軋機垂直振動問題研究進展[J].機械制造，2007(11):28-32.

[2] 侯福祥,張杰,曹建國. 帶鋼冷軋機振動問題的研究進展及評述[J].鋼鐵研究學報,2007(10):6-10+39.

[3] 聶榮光，朱偉鋒.軋機主傳動系統扭振建模及分析[J].有色金屬加工,2012(06):56-60.

[4] 黃彬城，馬維金，王俊元.高速軋機耦合振動問題研究進展及評述[J].制造業自動化，2013(12):55-58.

[5] 高崇一．考慮間隙和帶鋼振動的軋機主傳動系統非線性扭振研究[D]．秦皇島：燕山大學，2015．

[6] 黃永強.機械振動理論[M].北京：機械工業出版社，1996.

[7] 高菁．淺析有限元的應用[J].數字技術及應用,2012(02):207．

[8] 孫鵬．中厚板粗軋機主傳動系統動力學仿真及實驗研究[D].內蒙古:內蒙古科技大學，2011

[9] 商躍進.有限元原理與ANSYS實踐[M].北京：清華大學出版社，2012.

[10]張洪信．有限元基礎理論與ANSYS應用[M]．北京：機械工業出版社，2008．

[11]張志波．考慮帶材的軋機主傳動系統扭振研究[D]．秦皇島：燕山大學，2015．

[12]燕山大學軋機研究所.厚板軋機主傳動系統關鍵技術研究[R].秦皇島：燕山大學軋機研究所,2009.

[13]商大中.結構動力分析[M].哈爾濱：哈爾濱工程大學出版社，2005.

[14]張昭.有限元方法與應用[M].大連：大連理工大學出版社，2011.

Finite element analysis of the coupled vibrations of main drive system and strips

GUO Xiao-qiang1, DU Guo-jun2, LI Bo3

(1.College of Civil Engineering & Mechanics, Yanshan University, Qinhuangdao 066004, China； 2. College of Civil Engineering & Mechanics, Yanshan University, Qinhuangdao 066004, China； 3.Xi’an Modern Control Technology Research Institute, Xi’an, 710065, China)

Basic theory of ANSYS program and the property of SOLID186 structural units are introduced, and the relative parameter of coupled vibration is defined through ANSYS finite element program. The structure model of the main drive system and the strip for a rolling mill is built according to actual blueprint, and modal analyzed. The natural frequencies of the model and its mode shape are obtained, and carried out harmonic response analysis. Finally, the results proved that system structure begin resonance when the harmonic load frequency of the model is 8.4Hz, the model of the main drive system and the strip. And the results are referenced for the design and production of other similar rolling mills.

rolling mill; finite element analysis; torsional vibration; coupled vibration

2016-11-16；

2016-12-18

河北省高等學校科學技術研究項目(No.ZD2015077)

郭瀟檣(1989-)，男，山西人，碩士研究生，研究方向為軋機振動的有限元分析。

TG333

A

1001-196X(2017)03-0069-05