計及分布式電源的電能質量監測點優化配置

翁國慶 黃飛騰 南余榮 朱雙雙 楊曉東

（浙江工業大學信息工程學院 杭州 310023）

計及分布式電源的電能質量監測點優化配置

翁國慶 黃飛騰 南余榮 朱雙雙 楊曉東

（浙江工業大學信息工程學院 杭州 310023）

為實現智能配電網對電能質量（PQ）進行全面監測和擾動事件智能診斷，并考慮系統成本優化和分布式電源影響，分析了現有監測點配置方法存在的三個缺陷，提出需要同時考慮節點電壓凹陷域和電流信息全網可觀測的優化思路。改進了二進制粒子群優化算法（BPSO）的模型和步驟，并構建評價函數，提出一種基于改進粒子群優化的電能質量監測點配置的算法。通過改進的BPSO迭代，智能地布置監測點，實現了系統性能和經濟成本的最優化。最后，在四種不同結構的配電網絡中進行仿真應用。結果表明，該算法能有效地實現PQ監測點優化配置，以較低的成本實現了配電網的全面監測并滿足擾動事件智能診斷和精確定位的需求，且算法具有較好的收斂性和適用性。

電能質量 監測點 優化配置 改進粒子群優化 分布式電源

0 引言

隨著電力市場化不斷推進及敏感負荷快速增加，電力故障和電能質量（Power Quality, PQ）問題造成的經濟損失不斷增加。此外，隨著新能源的開發與利用，越來越多的分布式電源（Distributed Generator, DG）接入配電網，對電網節點電壓、功率潮流和電能質量等產生重大影響。電力供應的可靠性已成為當前智能電網領域的研究熱點[1]。對配電網進行全面監測有助于快速排除電力故障和解決PQ問題，降低經濟損失及明確事件責任，對供電可靠性具有重要意義[2,3]。

現有的電能質量監測儀（Power Quality Monitor, PQM）成本較高，從經濟上考慮，系統無法在所有節點均安裝PQM。但是，目前國內外對于PQM配置問題的研究仍存在一定的缺陷和較大的局限性。文獻[4,5]分別提出了建立在基爾霍夫電流準則（Kirchhoff Current Law, KCL）上的PQM優化配置方法，但未考慮電壓凹陷域問題。文獻[6]在前者的基礎上設計了一種網絡化PQ監測與分析系統。文獻[7-9]分別提出的基于狀態估計、粒子群算法以及改進模糊閾值的PQM優化配置方法，均忽略了電流信息的完備性。因此，現有方法無法滿足對PQ擾動事件的智能診斷和精確定位需求。

本文提出一種PQM配置優化思路：在節點電壓凹陷域的全網可觀測基礎上，同時兼顧電流信息的完備性，再依據線路的配電權重進行優化。改進了二進制粒子群優化算法（Binary Particle Swarm Optimization, BPSO）模型，構建了一種評價函數，并在算法流程中加入反饋校正環節，以提高算法效率。然后，采用改進的BPSO算法求取監測點配置最優方案，其目標函數是在實現系統性能和經濟優化的同時，能滿足PQ事件智能診斷和精確定位的要求。最后，利用Mtalab/Simulink軟件搭建了四種典型的、不同結構的含DG單元配電網模型，并進行了算法編程和仿真計算。

1 現有方法的缺陷

1.1 智能診斷的PQM配置需求

為實現智能配電網的PQ全面監測，必須對配電網中較大范圍的監測點進行PQ信息采集。各PQM應能進行電壓、電流等工頻信號電氣狀態量甚至波形的實時監測，進而實現對各種常規PQ指標的計算和擾動特征的提取，然后上傳PQ數據到系統PQ中心工作站。PQ中心工作站負責對區域內所有PQM上傳的PQ數據進行匯總，并融合工作站中存儲的系統結構、關鍵元件參數等關聯信息，實現系統級的數據處理和智能分析診斷功能，如PQ擾動源的精確定位。

PQ高級診斷和精確定位的一般步驟：首先，基于監測到擾動實時信息以及如小波變換、改進S變換、支持向量機（Support Vector Machine, SVM）[10]等高級處理分析方法，實現PQ擾動事件的智能分類辨識；然后，利用擾動功率法和擾動能量法等擾動方向判定算法，實現各PQM與PQ擾動源的相對位置（上、下游區域）判定；最后，融合配電網絡的拓撲結構信息和各PQM擾動方向判定信息實現PQ擾動源的精確定位。

對于最常見的能量吸收型PQ擾動事件，可采用有功擾動能量EΔ作為擾動特征值，其定義為

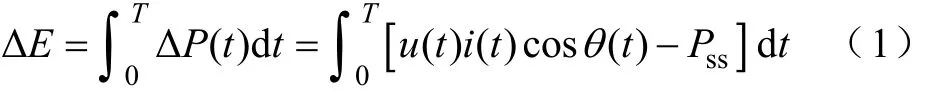
式中，()PtΔ為擾動功率；Pss為擾動發生初始時刻穩態有功功率（W）；()ut為電壓（V）；()it為電流（A）；()tθ為功角（°）；T為擾動始末時間間隔（s）。擾動方向判據為：當0EΔ＞時，擾動方向判定為下游；當0EΔ＜時，擾動方向判定為上游。

對應某個PQM，擾動方向判定算法[11]可根據配電網潮流方向，將整個網絡區域劃分為上游區域與下游區域，如圖1所示。

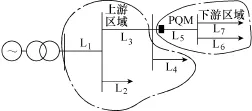
圖1 PQM 上、下游區域劃分Fig.1 Upstream and downstream regions of PQM

采用覆蓋矩陣Cl×m描述電網結構和PQM布置信息；采用擾動方向判別矩陣Dm×1表征所有PQM上傳的擾動方向判定信息。其中，l表示系統中的線段數量，m表示系統中實際配置PQM以及可用狀態估計獲得的虛擬PQM的總數。Cl×m中各元素值表示各線路與各PQM的相對位置關系；Dm×1中各元素值表示PQ擾動源與各PQM的相對位置關系。經矩陣運算Rl×1=Cl×mDm×1，得到結果矩陣Rl×1。PQ擾動源定位的判據為：擾動源所在位置Li對應的Rl×1元素值ri等于m。

因此，從PQ擾動分類、PQM擾動方向判定以及最后實現PQ擾動源精確定位的過程可知，為滿足PQ智能診斷要求，需同時滿足電壓和電流信息一定程度的完備性。但是，現有方法僅考慮了電壓或電流的單一條件全局可觀，不能滿足智能診斷的要求。

1.2 現有算法缺陷和應對策略

1.2.1 缺陷①：完備性條件考慮不夠充分

現有的PQM配置方法僅考慮電壓凹陷域或僅考慮KCL，只能適于電壓暫降的監測或者PQ擾動的初步判定，難以滿足高精確的診斷和定位要求。下面從兩種代表性的拓撲結構分析缺陷①，如圖2所示。

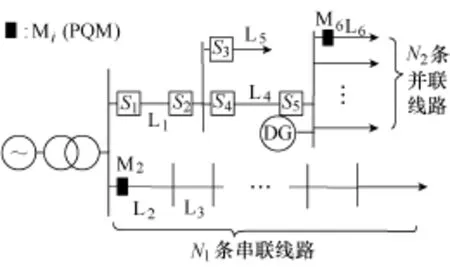
圖2 長線路和輻射狀線路Fig.2 Long lines and radial lines

一方面，N1條串聯而成的長線路，在其起始線路L2處安裝了PQM，基于KCL，整串線路的電流信息都可確定；但該長線路的末端將超出電壓暫降的可觀測域，使得末端處的電壓類型擾動事件無法被監測到。另一方面，N2條短線路并聯而成的輻射狀線路，在其中任一條線路（例如L6）處安裝PQM，則N2條短線路的電壓均可觀；但由于不明確電流信息過多，致使何處發生擾動無法確定。

此外，配置過程中還存在可選性問題。例如，圖2中L1、L4和L5上的5處方框位置，只需在{S1, S2}以及{S3, S4, S5}中選擇安裝2個PQM，即有6種方案可同時滿足該3條線路的電流和電壓均可觀的需求。

針對缺陷①的三個方面，本文提出了一種優化思路：同時考慮電壓和電流的可觀性，并依據由額度容量確定的配電權重進行優化。例如，根據線損和拓撲，可知S1＞S2且S4＞S5＞S3，則PQM配置的優化方案為S1和S4。考慮到由于L4末端的DG并網接入，將可能改變線路L4的潮流方向使得S5＞S4，則優化方案變為S1和S5。因此，DG的接入影響配置過程中的優先權分配。

文獻[8,9]均為基于普通PSO的優化配置方法，不僅具有現有文獻的普遍問題（缺陷①），而且其將普通的BPSO算法直接應用于優化配置中，還存在以下兩個缺陷。

1.2.2 缺陷②：二進制運算法則的適用性問題

普通粒子群算法中粒子位置x的第k+1次迭代運算式為

式中，上角標k或k+1代表迭代次數；x為粒子位置，是對應于可安裝PQM位置的一維向量（元素取值1或0，表示是否安裝PQM）。不失一般性，設k

x中存在一段連續為1且首位為0的值，而粒子的速度k

v中存在一段連續為0且末尾為1的值。由式（2）可得

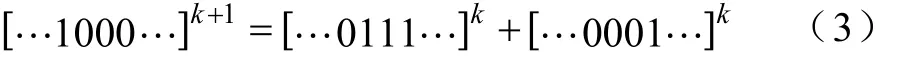
由式（3）可知，該用法對于優化配置問題存在明顯的不恰當之處。首先，xk的前三位011與vk速度000，表示這三個位置中僅安裝后兩個較優，而由于二進制的“進位”使xk+1取值反轉為100。其次，對于末位，位置1與速度1表明該位置安裝PQM的優先權較高，然而卻變為0。因此，直接運用普通BPSO模型，無法發揮出粒子群追隨當前較優粒子進行快速搜索的效果。

針對缺陷②，所提算法改進了PSO模型，修正了粒子位置與速度的迭代公式，可提高算法的適用性。

1.2.3 缺陷③：現有方法的評價函數過于簡化

現有方法提出的評價函數的基本思路是：從PQM安裝個數和滿足電壓暫降域全局可觀兩個角度去評價當前粒子。然而，其簡單化地將電壓可觀約束條件直接轉化為一個罰函數，若滿足則為0，不滿足則加上一個足夠大的懲罰因子。

這種構建思路，使得評價值兩極分化，僅能通過粒子群搜索的試湊性，在低維問題（簡單的拓撲結構）中有一定概率地找到較優解，但其效率很低，且在有限計算次數內易陷入局部極值。對于高維問題（復雜的拓撲結構），由于其簡單化的評價函數，配上適用性較差的未改進模型，收斂至最優解的概率極低。

針對缺陷③，提出了一種評價函數，不僅可滿足新優化思路的要求，且能配合改進的PSO模型，進而提高算法的收斂性。

2 改進的粒子群優化

所提算法的改進內容分為三個方面：①改進粒子群優化模型，提高適用性；②構建新的評價函數，提高收斂性；③加入基于可行域的反饋校正環節，提高算法效率。

2.1 改進的粒子群模型

在BPSO模型[12]中，各個粒子均為具有速度參數的一個解，其粒子位置對應于aN個可安裝位置的向量（向量維數a1N×），其元素取值為1或0（分別表示是否安裝PQM），所有這些問題的可行解構成了搜索空間中的位置狀態。各粒子的飛翔方向和距離由速度值和當前位置值決定，通過評價函數進行適應值評價，然后粒子群在解空間中追尋當前最優解進行快速搜索，找出最優粒子[13,14]。針對缺陷②對模型進行改進，改進后PSO模型的迭代過程如下。

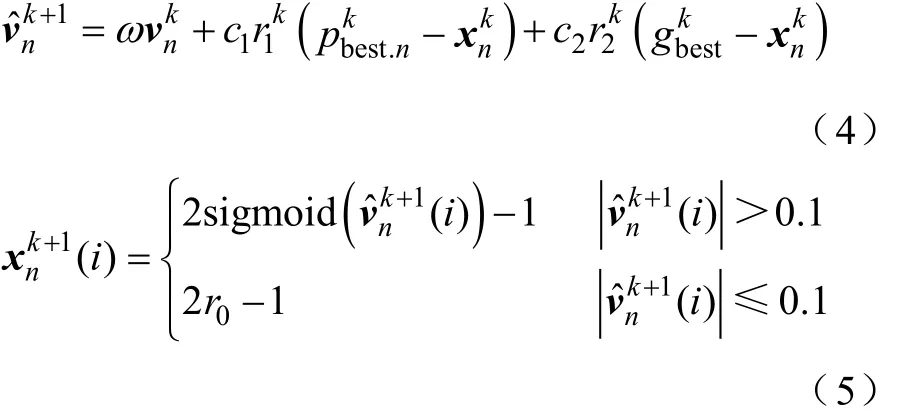
式中，下角標n表示第n個粒子；上角標k或k+1表示迭代次數；ω為慣性權重，代表速度的慣性系數；c1和c2為加速因子，代表粒子與當前較優位置的差距而產生加速的系數；r0、r1和r2為[0,1]區間的隨機實數；pbest.n為個體極值，表示第n個粒子當前找到過的最優位置；gbest為全局極值，表示所有粒子當前找到過的最優位置；v(i)為向量v的第i個元素，?i=1,2,…,Na；v?為中間變量，將復雜的迭代式分為兩條，使其表述明晰化；sigmoid(?)函數的定義為

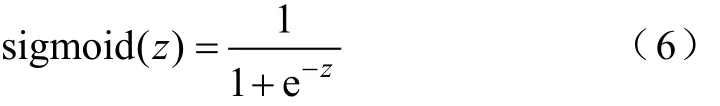
式中，z為任意變量。速度迭代式（4）表達了粒子群追隨當前較優粒子的特性，迭代式（5）用sigmoid(?)函數將速度的取值范圍轉換為區間[-1, 1]的連續值。r0的作用是防止速度趨近于零時，搜索長期停滯而陷入局部極值。

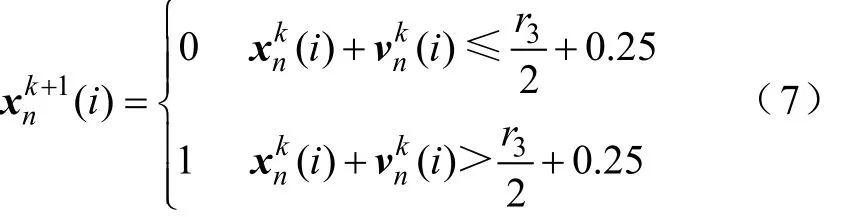
3粒子在第k+1次迭代時的第i個元素的取值。判斷條件的含義是：第k次粒子位置與其速度之和（取值范圍為[-1, 2]）若大于動態閾值，則第k+1次位置取值為1，否則為0，且每個元素分別計算。

模型改進的目的，是使算法在粒子迭代過程中，保持向當前較優粒子方向搜索的能力，克服二進制運算適用性問題，且閾值具有動態性能，防止過早陷入局部收斂。

2.2 評價函數構建

可觀測區域（Monitor Reach Area, MRA）是指系統發生PQ擾動事件時，該監測點所能觀測到該擾動事件的區域[15]。MRA也是節點電壓凹陷域的表達形式之一。實現全網的電壓可觀測性，即使系統監測點的MRA組合能夠覆蓋全網。系統全部節點的MRA采用一個Na×Fa維的0-1可觀測矩陣M表示，其元素賦值為

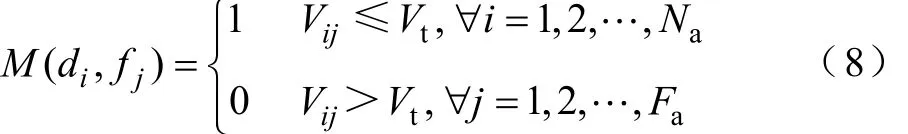
式中，Na為系統中可安裝PQM監測點數；Fa為系統中故障點數；Vij為故障點fj發生短路故障時di節點的電壓；Vt為設置的監測電壓閾值。M(di, fj)=1，表示故障點fj屬于節點di的MRA；M(di, fj)=0，表示故障點fj不屬于節點di的MRA。文獻[8,9,15]均給出了可觀測矩陣M的詳細計算方法，本文不再贅述。

對于電流的監測而言，PQM的優化配置通常要求符合以下兩條準則：①KCL，假設從一條母線上流出N條線路，一條支路的電流可通過另外N-1條支路計算得出，對于單個節點而言，N-1是避免支路電流不明確的PQM最少安裝個數；②PQM安裝在支路的起點（即剛從母線分離位置上），PQM監測范圍將包括整條線路。綜合兩條準則，可以得到全網符合N-1原則的最佳個數NKCL（通常NKCL＜Na）。

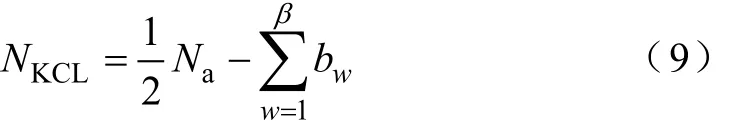
式中，β為系統中的母線數量；wb為第w條母線的判斷函數，當母線上連接兩條以上線路時，wb返回1，否則返回0。KCLN計算是基于基爾霍夫電流定律，在配電網的網絡拓撲中求出電流全局可觀的最小安裝個數。

從所提優化策略的三個方面來構建新的評價函數，將粒子群代入所構建評價函數計算適應值，對應的適應值越小，表示其解越優良。評價函數()knFx由四個子函數及其系數因子構成，即

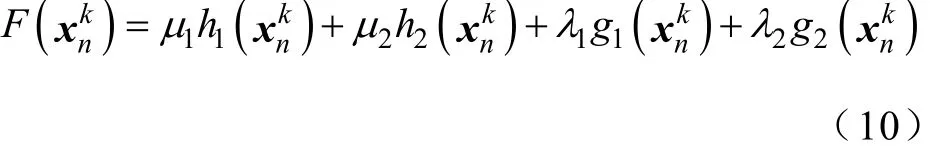
式中，μ1為單個PQM的成本因子；h1()為權重函數；μ2為不滿足N-1原則而產生的冗余因子；h2()為相應的冗余函數；λ1為不滿足MRA時的懲罰因子；g1()為相應的判定函數；λ2為覆蓋因子；g2(xk)為相應的覆蓋函數。

n

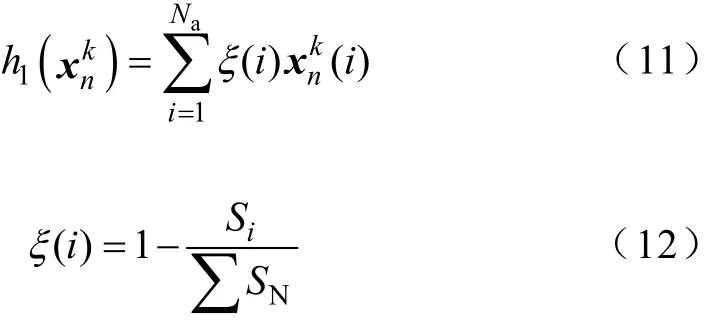
（1）權重函數h1()，表示對所有安裝PQM監測點進行的權重累加，若監測點數越少其值越小。式中，Si為第i個安裝點的額定容量；∑SN為所有額定容量總和；ξ(i)為xnk(i)對應的配電權重系數，其取值為略小于1的正數。配電權重系數是基于安裝點的額度容量占總容量的比例，再求出其與數值1的差值。一方面體現按配電權重進行優化的優先權，另一方面基于優化目標的評價函數是求極小值而進行的相對于標準數值1的差值轉換。因此，該系數越小表示其優先權的權重越大。

（2）冗余函數h2()，計算不滿足N-1原則而

產生的冗余度。

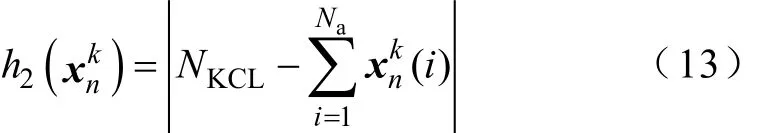
（3）判定函數g1()，用于判定是否滿足電壓

全局可觀。

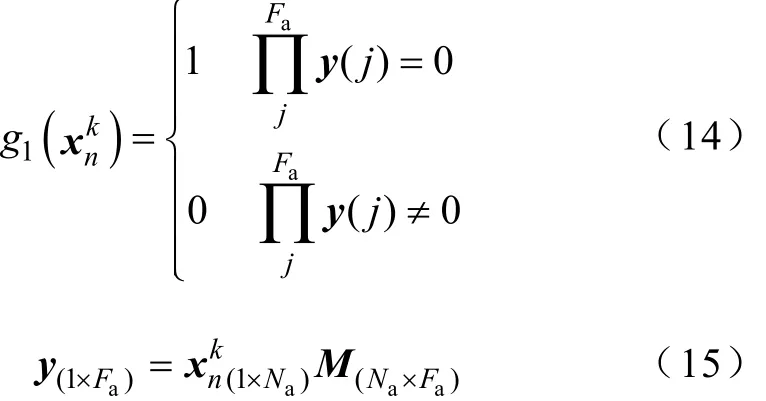
式中，y(j)為故障點被多個監測點同時監測到的個數，是向量y的第j個元素；y(1×Fa)為電壓可觀測矩陣M的1×Fa維向量y過渡中間向量。式（15）用下角標注釋了運算維數，若xkM的運算結果y中存

n在數值為0的項，表明當前解（配置方案）在對應的行列處存在無法監測到的故障點，則式（14）的連乘積條件將等于0，使得判定返回值等于1，進而觸發評價函數式（10）中的懲罰因子λ1。

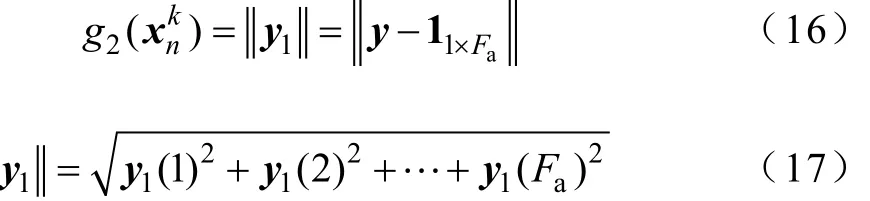
（4）覆蓋函數g2()表示監測點利用效率。式中，y1為求向量y1的歐氏范數；11×Fa代表1×Fa維的全1向量。當y1的歐氏范數趨近于零時，表明所有監測點的利用率最高（所有故障點均可監測且僅被一個監測點測到）；反之，其范數越大，表明存在過多的監測點被覆蓋在配電網的某塊區域。

式（10）～式（17）所表達的評價函數，其目標是求取在同時滿足可觀測矩陣和N-1原則的情況下，PQM的利用率最高和總成本最低；且在同等情況下，優先布置配電權重較高的安裝點。粒子位置越符合要求的目標，將其代入評價函數得到的適應值越小。

2.3 帶反饋校驗的算法流程

基于改進BPSO的優化配置算法流程如圖3所示，可分為三塊區域：①初始化區域；②可行域反饋區域；③迭代搜索區域。

改進BPSO流程中，增加了可行域的反饋校驗環節，可行域條件設置為安裝PQM數量不少于NKCL。具體步驟如下。

（1）參數初始化。確定粒子群規模nmax和最大迭代次數Tmax，并設置其慣性權重、加速因子、成本因子、冗余因子、懲罰因子和覆蓋因子等初始參數。

（2）確定符合N-1原則的PQM數量NKCL；根據拓撲結構和四種故障類型得到對應的可觀測矩陣M。

（3）根據可安裝點的容量比重，計算其配電權重。

（4）粒子群位置和速度初始化，在保證多樣性情況下進行隨機賦值。

（5）將所有粒子群代入評價函數式（10），計算適應值，并對初始的極值進行賦值。

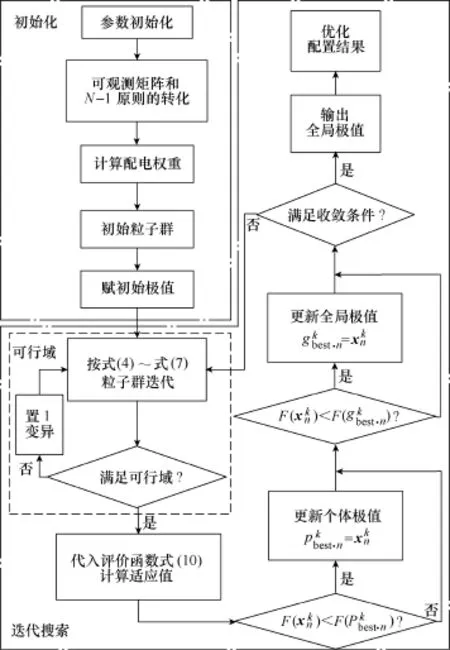
圖3 改進BPSO算法流程Fig.3 Flow chart of the improved BPSO

（6）根據式（4）～式（7），迭代更新所有粒子的位置和速度。

（7）可行域的反饋校驗環節。判斷粒子的安裝個數不少于KCLN，若不滿足可行域，則對該粒子的隨機一個元素()knix置1變異，再反饋校驗，直到滿足位置。

（8）將滿足可行域的所有粒子群，代入評價函數式（10）計算適應值。

（9）若粒子的適應值優于此前的個體極值，則更新個體極值，否則不變。

（10）若最佳的個體極值優于此前的全局極值，則更新全局極值，否則不變。

（11）若達到最大迭代次數，則輸出全局最優粒子；否則返回步驟（6）。

（12）根據輸出的全局最優粒子的元素值，按其取值為0或1來確定對應位置是否安裝PQM，并累加其所有元素值得到安裝PQM總個數。

所提算法的機理為利用改進的粒子群迭代進行快速搜索，迭代過程中用評價函數式篩選出滿足PQ全局可觀測（包含電壓和電流）的PQM最優配置方案，其中添加的可行域反饋校驗環節，用于提高算法效率。

3 算例仿真

對應于四種典型的配電網拓撲結構[16]，引入DG單元，采用Matlab/Simulink電力系統模塊構建仿真模型，并進行改進BPSO算法的編程，進行PQM優化配置應用，得到優化結果。

圖4為“含DG的11節點配電網”仿真模型中PQM監測到的波形，結構如圖5所示。監測點位于線路L1，PQ擾動源位于線路L6，擾動事件為能量注入型的大電容短時投切。

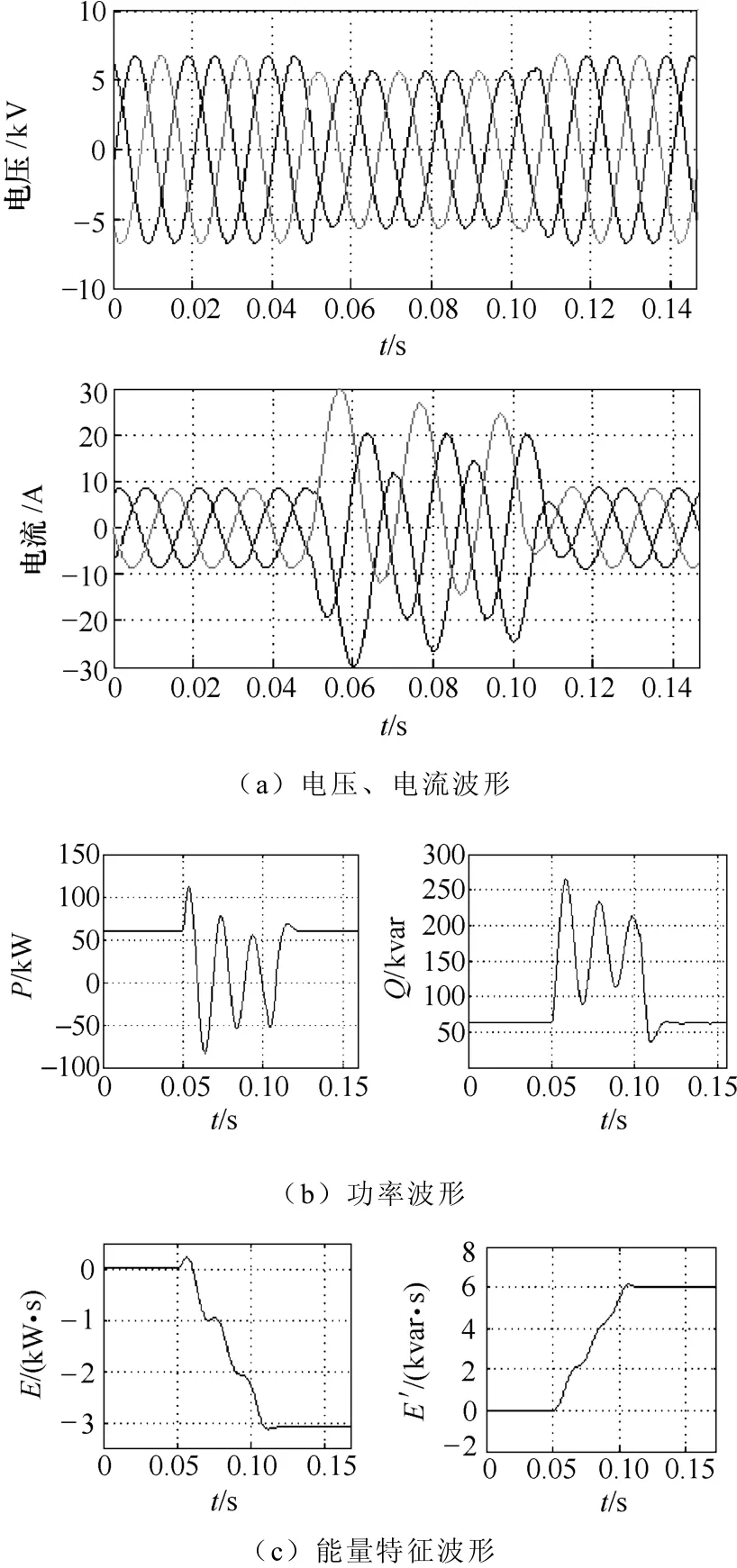
圖4 PQ擾動事件的波形Fig.4 Waveforms of PQ disturbance event

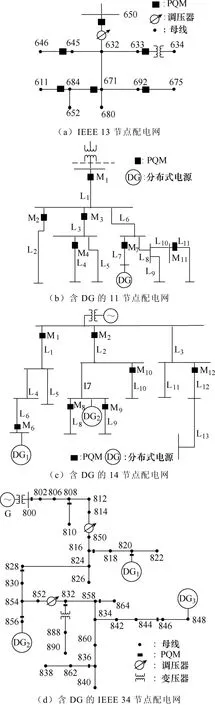
圖5 四種配電網的PQM優化配置結果Fig.5 Optimal allocations of four distribution networks

圖4a為擾動事件持續時間內的電壓暫降、沖擊電流波形以及擾動事件發生前后的穩態工頻波形；圖4b為擾動事件的有功功率P和無功功率Q波形；圖4c為有功、無功擾動能量E、E′的特征波形，用于PQ診斷和精確定位。此時，有功擾動能量為負，且擾動類型為能量注入型，判定擾動方向為其下游。

圖6顯示了其中IEEE 13節點配電網PQM配置優化過程中粒子群個體極值的適應值收斂過程。圖6中，粒子群種群數量設置為40，迭代次數設置為300，每5次迭代標注一個“*”符號（為保持圖形的清晰度）。從圖6a的總體趨勢可以看出，個體極值的適應值以類似于指數的規律衰減，不斷逼近全局最優解。粒子向當前較優位置的追隨效果，使得算法具有較快的收斂速度。如圖6中第100～150次迭代過程中，可以清晰地觀察到一部分位置較差的粒子在追隨作用下，跳出局部收斂區域，快速地逼近最優解。圖6b中全局極值的收斂過程，也顯示了其收斂速度接近于指數收斂。

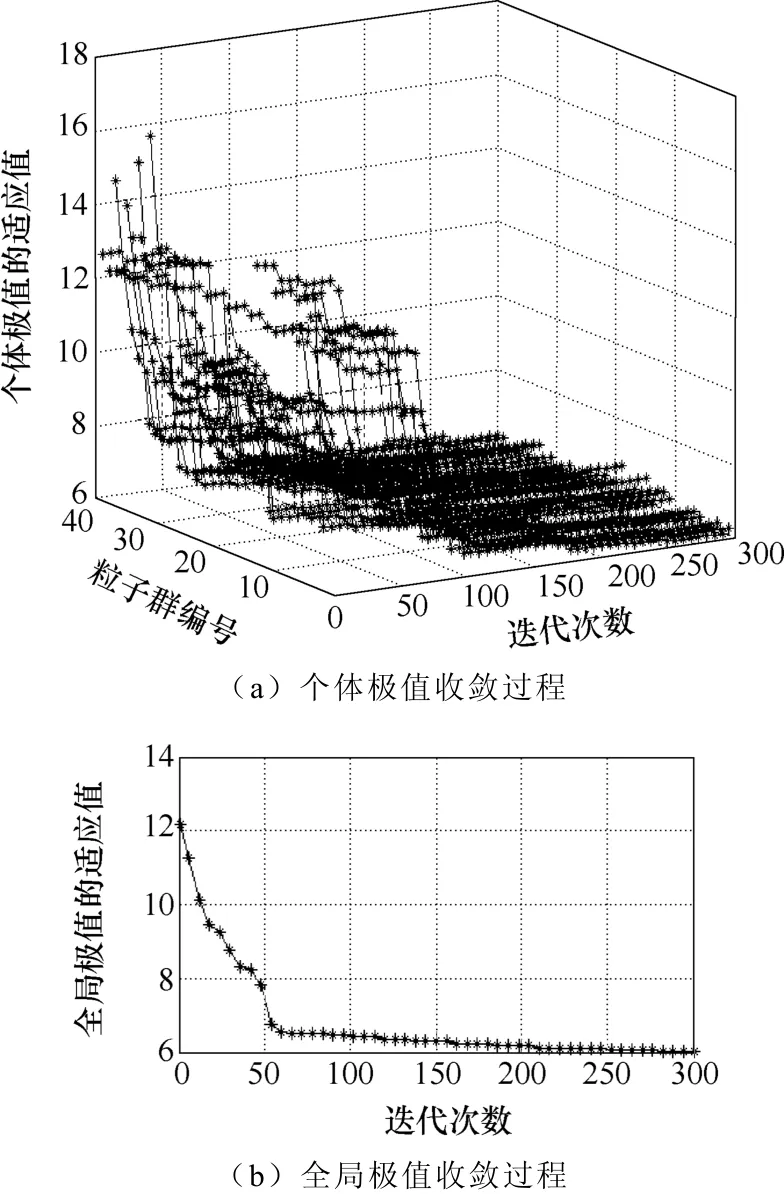
圖6 改進粒子群算法收斂過程Fig.6 Convergence process of the BPSO

根據容量計算IEEE 13節點配電網的配電權重，部分參數見表1。表1中，650-632表示從650向632的母線出線位置，第3列“容量總和”是所有可安裝位置的容量之和（包括反向節點），而不僅是表中的第2列代表性數據之和。

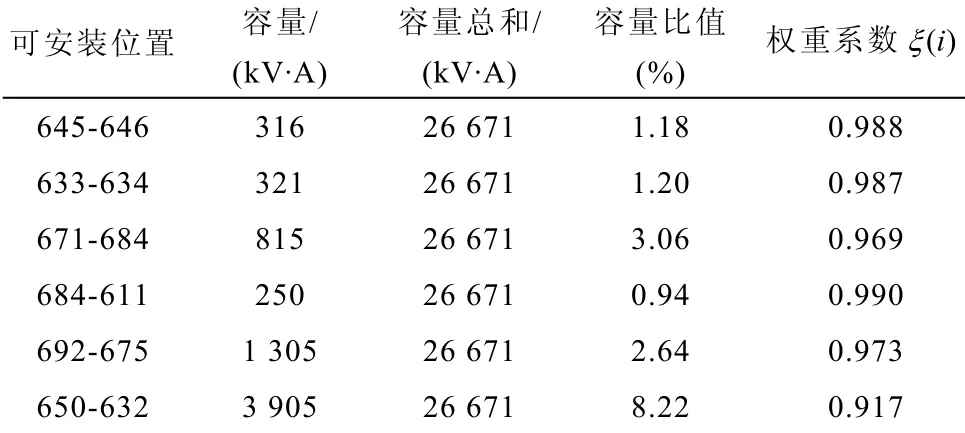
表1 配電權重計算參數Tab.1 Calculation parameters of distribution weights

通過改進算法的優化，將得到的四種不同配電網結構的配置結果標注在其拓撲中，如圖5所示。根據圖5中PQM位置分布，從整體結構和區域覆蓋上分析，四種優化結果的覆蓋率都比較均衡。

驗算其是否均同時符合N-1電流原則和MRA電壓可觀測條件。驗算方法為：首先根據式（9）驗算PQM總個數是否等于（或大于）最佳個數KCLN，并驗算任一條未安裝PQM的線路是否可以根據KCL定律由已安裝PQM推算得到其電流信息；然后按照式（8）的MRA矩陣，驗算其是否符合電壓全局可觀；最后，根據算法的覆蓋效率和節省率，來評判其經濟成本的優化效果。

根據圖5所示PQM配置方案，在PQ監測系統的分析功能上，可進一步獲得未安裝PQM位置的PQ信息以及滿足擾動事件診斷和精確定位的需求。圖5還表明，所提算法能適用于不同數量DG并網接入的情況。從拓撲結構上，可得到四種模型中可安裝的位置數（節點的出線位置）、DG的數量和位置，PQM優化安裝位置和數量，結果見表2。

表2表明，改進算法能有效地對PQM進行優化配置，在滿足全網PQ監測的前提下，降低實際配置的PQM數量，從而降低PQ監測系統的構造成本。優化節省率比較如圖7所示。

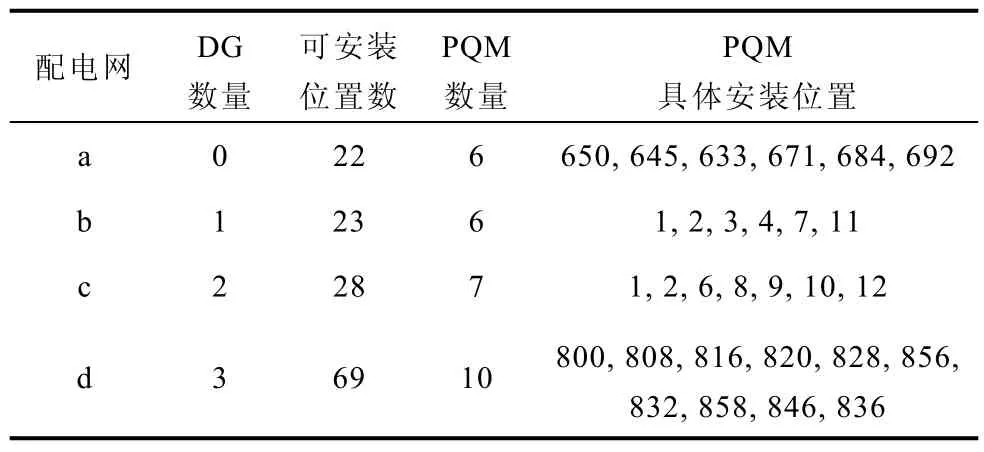
表2 PQM優化數量和位置Tab.2 Number and location of PQMs

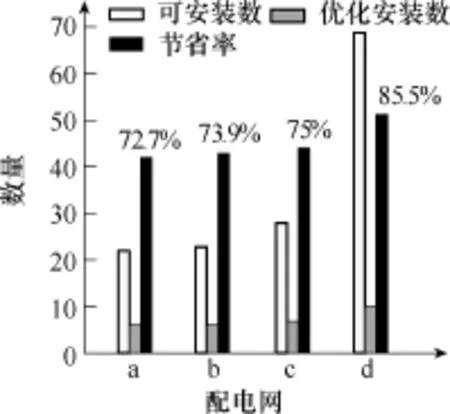
圖7 優化節省率比較Fig.7 Comparison of optimization efficiency

隨著配電網結構復雜程度（可安裝數）的提升，通過比較可安裝位置與實際安裝數量的差值，可知四種配電網的節省率都有所增高。這表明本算法具有較強的適用性，且對于復雜的配電網優化效果更好。以圖5a所示IEEE 13節點配電網為例，對僅考慮電流可觀或電壓可觀的兩類現有算法以及所提新算法的配置結果進行比較，結果見表3。

表3 配置結果比較Tab.3 Comparison of allocation results

表3結果表明，現有算法不能同時符合N-1電流原則和MRA電壓可觀測條件；而本文算法可以滿足兩者均可觀，且具有較好的覆蓋利用率。

圖8比較了基于粒子群的智能算法收斂性能，包括普通粒子群法[7]、模糊閾值法[9]及本文算法。圖8中，收斂成功率是指在限定的評價次數（粒子群規模數與迭代次數的乘積）內，收斂到該算法能達到的最佳優化效果的成功次數。由于本文算法針對現有方法的缺陷②和缺陷③進行了多方面改進，且增加了可行域反饋校正環節，提高了評價函數的有效計算次數，使得其收斂性能優勢顯著。

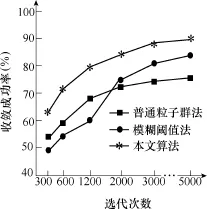
圖8 收斂性能比較Fig.8 Comparison of convergence

綜合考慮上述各方面特點，對所提算法與現有算法的比較見表4，其中覆蓋效率由覆蓋函數換算成百分比得到。

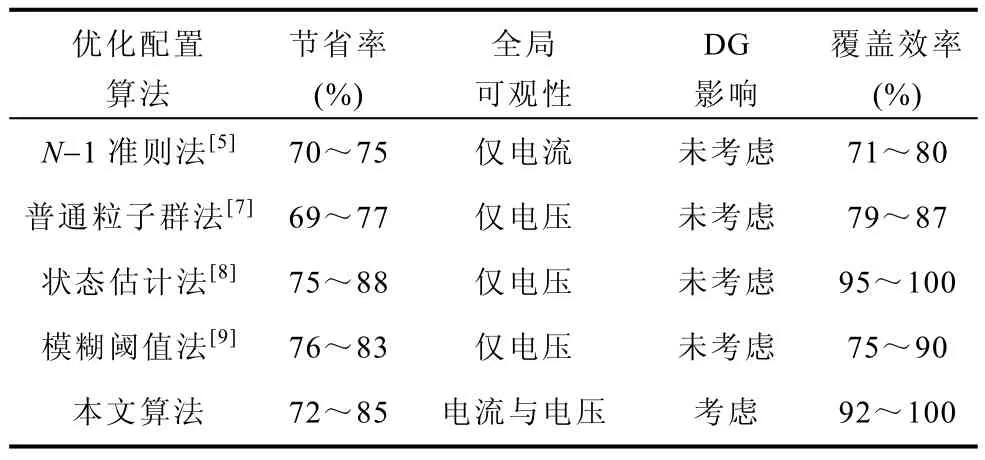
表4 五種算法綜合比較Tab.4 Comprehensive comparison of five algorithms

表4結果表明，雖然現有算法的節省率在65%～88%之間，且狀態估計法的覆蓋效率更高，但其不滿足電壓和電流的同時全局可觀，且未考慮DG的并網影響，其中直接采用粒子群的算法還存在收斂性較差的問題。而所提改進算法不僅考慮了這些因素，而且收斂性較好，跳出局部收斂的能力較強。合理構建的新評價函數，使其優化結果能較好地符合期望目標的要求，并具有較好的適用性和節省率。

4 結論

考慮到可靠供電對社會經濟發展的重要性，以及配電網智能化和新能源技術發展過程中面臨的挑戰，對智能配電網進行PQ全面監測具有必要性。針對現有PQ監測點優化布置算法的缺陷，提出了一種PQM優化布置思路。不僅改進了BPSO模型，構建了一種新的評價函數，并提出一種基于改進BPSO的PQM優化配置算法。在四種不同結構的配電網絡上進行仿真，結果表明該算法收斂速度較快并具有較好的通用性，能自動、有效地實現PQ監測系統的監測點優化配置，且能適用于DG并網的情況。本文算法以較低的成本實現了配電網的PQ全面監測，并滿足PQ擾動事件的智能診斷和精確定位需求，克服了現有算法的局限性。

[1] MBarr J, Majumder R. Integration of distributed generation in the Volt/VAR management system for active distribution networks[J]. IEEE Transactions on Smart Grid, 2015, 6(2)： 576-586.

[2] 劉蓓, 汪沨, 陳春, 等. 和聲算法在含DG配電網故障定位中的應用[J]. 電工技術學報, 2013, 28(5)：280-286. Liu Bei, Wang Feng, Chen Chun, et al. Harmony search algorithm for solving fault location in distribution networks with DG[J]. Transactions of China Electrotechnical Society, 2013, 28(5)： 280-286.

[3] Chenine M, Ullberg J, Nordstrom L, et al. A framework for wide-area monitoring and control systems interoperability and cybersecurity analysis[J]. IEEE Transactions on Power Delivery, 2014, 29(2)：633-641.

[4] Won D, Chung I, Kim J, et al. A new algorithm to locate power-quality event source with improved realization of distributed monitoring scheme[J]. IEEE Transactions on Power Delivery, 2006, 21(3)： 1641-1647.

[5] Won D, Ahn S, Chung I, et al. A new algorithm to find the optimal numbers and locations of power quality monitors[C]//IEEE Russia Power Tech, 2005：1-7.

[6] 翁國慶, 張有兵. 網絡化電能質量監測與分析系統的設計[J]. 電力系統自動化, 2008, 32(15)： 79-83. Weng Guoqing, Zhang Youbing. Design of a networked power quality monitoring and analysis system[J]. Automation of Electric Power Systems, 2008, 32(15)： 79-83.

[7] 周超, 田立軍. 基于粒子群優化算法的電壓暫降監測點優化配置[J]. 電工技術學報, 2014, 29(4)： 181-187. Zhou Chao, Tian Lijun. An optimum allocation method of voltage sag monitoring nodes based on particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(4)：181-187.

[8] Ali S, Wu K, Weston K,et al. A machine learning approach to meter placement for power quality estimation in smart grid[J]. IEEE Transactions on Smart Grid, 2015, 6(6)： 542-547.

[9] 唐亞迪, 徐永海, 洪旺松. 基于模糊控制模型的電壓暫降監測裝置優化配置[J]. 電力自動化設備, 2015, 35(8)： 1-7. Tang Yadi, Xu Yonghai, Hong Wangsong. Allocation optimization based on fuzzy control model for voltage-sag monitors[J]. Electric Power Automation Equipment, 2015, 35(8)： 1-7.

[10] 徐志超, 楊玲君, 李曉明. 基于聚類改進S變換與直接支持向量機的電能質量擾動識別[J]. 電力自動化設備, 2015, 35(7)： 50-58, 73. Xu Zhichao, Yang Lingjun, Li Xiaoming. Power quality disturbance identification based on clusteringmodified S-transform and direct support vector machine[J]. Electric Power Automation Equipment, 2015, 35(7)： 50-58, 73.

[11] 黃飛騰, 翁國慶, 王強. 帶分布式電源的配電網電能質量擾動源定位[J]. 電力系統自動化, 2015, 39(9)： 150-155. Huang Feiteng, Weng Guoqing, Wang Qiang. Location of power quality disturbance source on distribution network with distributed generation[J]. Automation of Electric Power Systems, 2015, 39(9)： 150-155.

[12] Ganguly S. Multi-objective planning for reactive power compensation of radial distribution networks with unified power quality conditioner allocation using particle swarm optimization[J]. IEEE Transactions on Power System, 2014, 29(4)： 1801-1810.

[13] 王曦, 李興源, 趙睿. 基于相對增益和改進粒子群算法的PSS與直流調制協調策略[J]. 中國電機工程學報, 2014, 34(34)： 6177-6184. Wang Xi, Li Xingyuan, Zhao Rui. Coordination strategy of PSS and DCM based on relative gain and improved PSO[J]. Proceedings of the CSEE, 2014, 34(34)： 6177-6184.

[14] Shen M, Zhan Z, Chen W, et al. Bi-velocity discrete particle swarm optimization and its application to multicast routing problem in communication networks[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12)： 7141-7151.

[15] Ibrahim A A, Mohamed A, Shareef H, et al. A new approach for optimal power quality monitor placement in power system considering system topology[J]. Przeglad Elektrotechniczny, 2012, 88(9a)： 272-276.

[16] IEEE PES distribution system analysis subcommittee's distribution test feeder working group[OL]. http：//ewh.ieee.org/soc/pes/dsacom/testfeeders/index. html.

（編輯 張洪霞）

Optimize Allocation of Power Quality Monitoring Sites with Distributed Generators

Weng Guoqing Huang Feiteng Nan Yurong Zhu Shuangshuang Yang Xiaodong
（College of Information Engineering Zhejiang University of Technology Hangzhou 310023 China）

In order to comprehensively achieve monitoring and diagnosis of the power quality disturbance events in the smart grid as well as consider the optimization of system costs and the interconnection of distributed generators, this paper analyzes the deficiencies of the existing optimal allocation methods for the power quality (PQ) monitors. The model and steps of the binary particle swarm optimization (BPSO) are improved, and a new evaluation function is constructed. Considering the entirely observable network in the domain of the node voltage sag and the completeness of the current information, a novel allocation method based on improved particle swarm optimization is proposed. The improved BPSO is used to iterate the optimal allocation of PQ monitoring sites. Thus the system optimization between the performance and the costs is achieved. Finally, the simulations are carried out using four kinds of distribution networks. The results show that, with fast convergence and good applicability, the proposed algorithm can effectively achieve the diagnosis and optimal allocation of the PQ monitoring sites at a low cost.

Power quality, monitoring sites, optimal allocation, improved particle swarm optimization, distributed generators

TM711

翁國慶 男，1977年生，博士，副教授，研究方向為電能質量監控、電力自動化與智能電網等。

E-mail： wgq@zjut.edu.cn

黃飛騰 男，1984年生，博士研究生，實驗師，研究方向為智能電網、分布式能源與優化算法等。

E-mail： hfate@zjut.edu.cn（通信作者）

10.19595/j.cnki.1000-6753.tces.151913

國家自然科學基金（51207139、51407160），浙江省自然科學基金（LY17E070005）和浙江工業大學創新性實驗項目（ZJ201619）資助。

2015-11-27 改稿日期2016-01-16