信用風(fēng)險(xiǎn)分類預(yù)測(cè)單一模型研究及實(shí)證分析

鄒柏松

(中南民族大學(xué) 經(jīng)濟(jì)學(xué)院，湖北 武漢 430074)

?

信用風(fēng)險(xiǎn)分類預(yù)測(cè)單一模型研究及實(shí)證分析

鄒柏松

(中南民族大學(xué) 經(jīng)濟(jì)學(xué)院，湖北 武漢 430074)

目前，我國(guó)商業(yè)銀行所面臨的信用風(fēng)險(xiǎn)隨著信貸業(yè)務(wù)的不斷發(fā)展而逐步增加，如何對(duì)企業(yè)信用風(fēng)險(xiǎn)進(jìn)行有效區(qū)分和管理，是商業(yè)銀行亟待解決的問題。基于此，本文依據(jù)信用評(píng)估指標(biāo)體系分別對(duì)Logistic回歸模型、貝葉斯判別模型、支持向量機(jī)模型這三類模型進(jìn)行了設(shè)計(jì)與構(gòu)建，同時(shí)對(duì)三類模型分別進(jìn)行實(shí)證分析和結(jié)果評(píng)價(jià)，從分類準(zhǔn)確率和模型穩(wěn)健性兩方面對(duì)結(jié)果進(jìn)行比較，作為進(jìn)一步建立組合分類預(yù)測(cè)模型的基礎(chǔ)。本文的研究成果，有利于推動(dòng)我國(guó)商業(yè)銀行信用風(fēng)險(xiǎn)定量度量方法的研究，從而有助于提高商業(yè)銀行的風(fēng)險(xiǎn)控制水平，使得不良資產(chǎn)得以降低，在提高我國(guó)商業(yè)核心競(jìng)爭(zhēng)力以及促進(jìn)消費(fèi)信貸市場(chǎng)的發(fā)展等方面有巨大的意義。

單一模型；信用風(fēng)險(xiǎn)；統(tǒng)計(jì)方法；數(shù)據(jù)挖掘

一、引言

近年來，我國(guó)信用風(fēng)險(xiǎn)管理水平正在逐步提升，可是隨著金融業(yè)對(duì)外資銀行政策的逐步開放，我國(guó)的商業(yè)銀行所需面對(duì)的國(guó)際和國(guó)內(nèi)競(jìng)爭(zhēng)壓力越來越大，在如今這樣嚴(yán)峻的內(nèi)外形勢(shì)的考驗(yàn)下，為了和國(guó)際接軌，需要研究構(gòu)建以計(jì)量模型為基礎(chǔ)的信用風(fēng)險(xiǎn)管理系統(tǒng)，從而有效和全面地控制風(fēng)險(xiǎn)。

隨著我國(guó)商業(yè)銀行信貸業(yè)務(wù)的不斷發(fā)展，銀行將面臨更大的信用風(fēng)險(xiǎn)，如何對(duì)企業(yè)信用風(fēng)險(xiǎn)進(jìn)行有效區(qū)分和管理，是商業(yè)銀行亟待解決的問題。尤其是我國(guó)信用風(fēng)險(xiǎn)管理體系還不夠完善，關(guān)于信用風(fēng)險(xiǎn)的度量方法多是借鑒國(guó)外現(xiàn)有模型，針對(duì)這一情況，本文結(jié)合上市公司財(cái)務(wù)指標(biāo)數(shù)據(jù)，選取目前廣泛應(yīng)用的Logistic回歸、貝葉斯判別法等統(tǒng)計(jì)方法和支持向量機(jī)模型等數(shù)據(jù)挖掘方法，分別比較其實(shí)證結(jié)果的優(yōu)劣。

二、基于logistic回歸的信用風(fēng)險(xiǎn)分類預(yù)測(cè)模型

1.二項(xiàng)Logistic回歸模型原理

Logistic函數(shù)，即為增長(zhǎng)函數(shù)，在個(gè)人信用評(píng)估這一方面，Logistic回歸的應(yīng)用相對(duì)來說已經(jīng)比較成熟，同時(shí)普遍認(rèn)為在諸多統(tǒng)計(jì)學(xué)方法中穩(wěn)健性和精確性較高，在分類問題中具有較好的特性。由于本文中輸出變量只有0和1兩個(gè)值，因此文中采用二項(xiàng)Logistic回歸模型進(jìn)行建模和預(yù)測(cè)，模型可以在充分借鑒一般線性回歸模型的理論和思路的基礎(chǔ)上轉(zhuǎn)換而來。

首先，對(duì)于一元線性回歸模型yi=β0+βixi+εi，其回歸方程E(yi)=β0+βixi是對(duì)輸出變量均值的預(yù)測(cè)。當(dāng)輸出變量為0/1二分類變量時(shí)，如果仍采用一元線性回歸模型建立回歸方程，則是對(duì)輸入變量為xi時(shí)輸出變量yi=1的概率的預(yù)測(cè)。由此給出的啟示是：可利用一般線性回歸模型(可以是一元，也可是多元)對(duì)輸出變量取值為1的概率P進(jìn)行建模，這時(shí)候，回歸方程所輸出的變量其取值范圍為0～1，回歸方程的一般形式如下所示：

(1)

在應(yīng)用到實(shí)際的過程中，它們之間通常是非線性關(guān)系，一般情況下都和增長(zhǎng)函數(shù)一致，所以應(yīng)該采用非線性轉(zhuǎn)換來處理概率P的轉(zhuǎn)換。通過上述分析，進(jìn)行的兩步處理如下：

(1)把P轉(zhuǎn)換為Ω

(2)

其中，Ω是指發(fā)生比或者相對(duì)風(fēng)險(xiǎn)，表示某一事件發(fā)生和不發(fā)生概率之間比值，Ω值越高，相關(guān)公司就越有可能違約，Ω值的取值范圍介于0和+∞之間。

(2)把Ω轉(zhuǎn)換為lnΩ

(3)

其中，lnΩ被稱為L(zhǎng)ogitP。經(jīng)過這個(gè)步驟的轉(zhuǎn)換之后，LogitP和Ω之間依舊呈現(xiàn)出一致的或增長(zhǎng)或下降的關(guān)系。

這兩個(gè)步驟的轉(zhuǎn)換被稱為L(zhǎng)ogit變換，經(jīng)過Logit變換，就能夠完成在一般線性回歸模型中構(gòu)建輸出變量以及輸入變量間的多元分析模型的過程，即

(4)

稱式(4)為L(zhǎng)ogistic回歸方程，顯然LogitP與輸入變量之間是線性關(guān)系。將Ω代入，有

(5)

于是有

(6)

上式(6)是十分有代表性的增長(zhǎng)函數(shù)，主要體現(xiàn)出了概率P以及輸入變量它們兩者的非線性關(guān)系。

Madalla就曾經(jīng)選擇運(yùn)用Logistic模型來進(jìn)行非違約和違約貸款申請(qǐng)人的區(qū)分，通過研究得出，在違約概率P<0.551的情況下屬于非風(fēng)險(xiǎn)貸款，在違約概率P≥0.551的情況下屬于風(fēng)險(xiǎn)貸款，本文中也將該判別標(biāo)準(zhǔn)應(yīng)用于ST類公司和非ST類公司的判定中。

Logistic回歸模型的參數(shù)估計(jì)通常采用極大似然法來計(jì)算，具體算法如下：

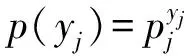
(7)

式(7)即為似然函數(shù)。對(duì)該似然函數(shù)取對(duì)數(shù)得到：

(8)

通過上式得到的βi(i=1,…,k)的估計(jì)值就是極大似然估計(jì)。通過證明得出，在樣本隨機(jī)時(shí)，漸進(jìn)正態(tài)性、有效性和相合性等是Logistic回歸模型的極大似然估計(jì)的重要特點(diǎn)，它一方面解決了線性回歸方法之中的部分缺陷，另一方面它的實(shí)際意義也能夠通過相對(duì)風(fēng)險(xiǎn)十分明顯地體現(xiàn)出來。

2.Logistic模型實(shí)證分析

本文利用Clementine軟件進(jìn)行建模和預(yù)測(cè)，為避免變量之間的多重共線性，采取逐步回歸的方法建立模型，對(duì)測(cè)試樣本重復(fù)10次2-折交叉驗(yàn)證來評(píng)估模型的準(zhǔn)確率，其基本的流程如圖1、圖2所示：

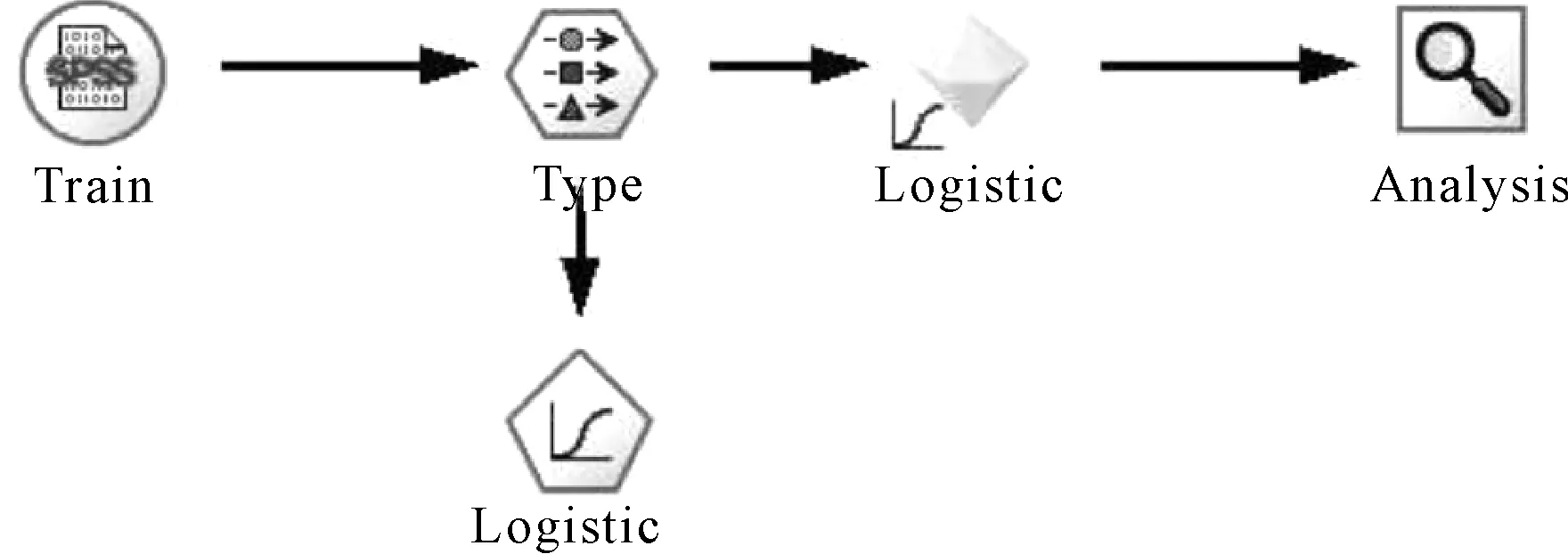
圖1 Logistic訓(xùn)練模型圖

圖2 Logistic測(cè)試模型圖

10次建模和預(yù)測(cè)得到的預(yù)測(cè)準(zhǔn)確率及穩(wěn)定性評(píng)估值如表1所示：

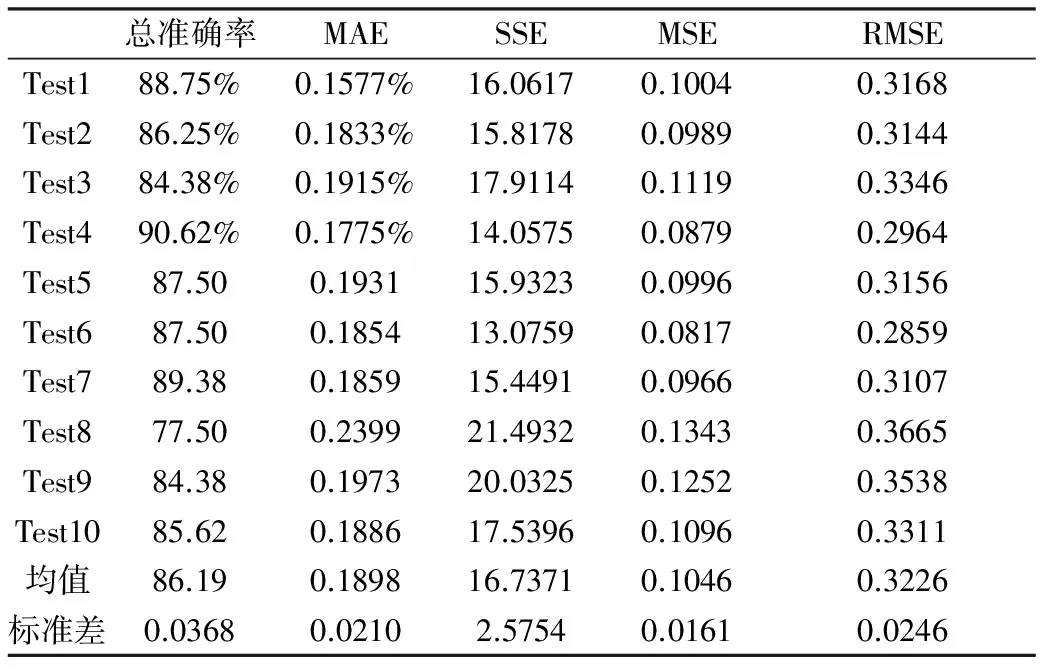
表1 Logistic模型預(yù)測(cè)結(jié)果

其模型收益(Gain)曲線圖如下：

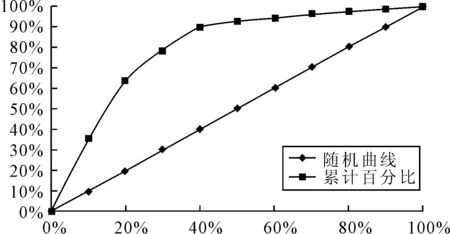
圖3 Logistic訓(xùn)練模型圖

(注：由于本文采取10次2-折交叉驗(yàn)證的方法，因此10次結(jié)果的平均值是用來進(jìn)行Gain圖繪制的數(shù)據(jù)，下同)

其中隨機(jī)曲線表示在完全隨機(jī)的情況下一定百分比的數(shù)據(jù)能夠預(yù)測(cè)出的ST類公司的百分比，顯然，這是一條45度傾斜的直線。由圖3看出，大約30%的數(shù)據(jù)就可以預(yù)測(cè)出80%的ST類公司(標(biāo)記值為“1”)，分類預(yù)測(cè)的效果較好。

三、基于貝葉斯(Bayes)判別的信用風(fēng)險(xiǎn)分類預(yù)測(cè)模型

1.貝葉斯(Bayes)判別的基本原理

貝葉斯判別包含于貝葉斯方法的范圍之內(nèi)，貝葉斯方法主要是對(duì)不確定性進(jìn)行研究的一種推理方法，其中用貝葉斯概率來對(duì)不確定性進(jìn)行詳細(xì)的表示，而且貝葉斯概率屬于一種主觀概率。通常，經(jīng)典概率反映的是事件的客觀特征，這一概率不會(huì)隨人們主觀意識(shí)的變化而變化，而貝葉斯概率則不同，它是人們對(duì)事物發(fā)生概率的主觀估計(jì)。

首先假設(shè)已經(jīng)對(duì)研究的對(duì)象有了一定程度上的認(rèn)識(shí)是貝葉斯判別法的基本思想，先驗(yàn)概率通常被用來對(duì)這種認(rèn)識(shí)進(jìn)行描述。對(duì)于多個(gè)總體的判別來說，不是考慮構(gòu)建判別式，而是對(duì)待判樣本屬于各總體的條件概率p(l|x),l=1,2,…,k進(jìn)行計(jì)算，對(duì)k個(gè)概率的大小進(jìn)行比較，之后再把判定新樣本來自概率最大的那一個(gè)總體。

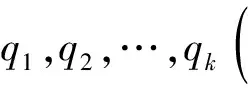
(10)

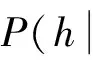
(1)訓(xùn)練樣本的觀測(cè)值

設(shè)個(gè)體分為k類，并分別從第g類中抽得ng(g=1,2,…,k)個(gè)訓(xùn)練樣本，p個(gè)屬性值，依次用x1,x2,…,xp表示，觀測(cè)值如表2所示：

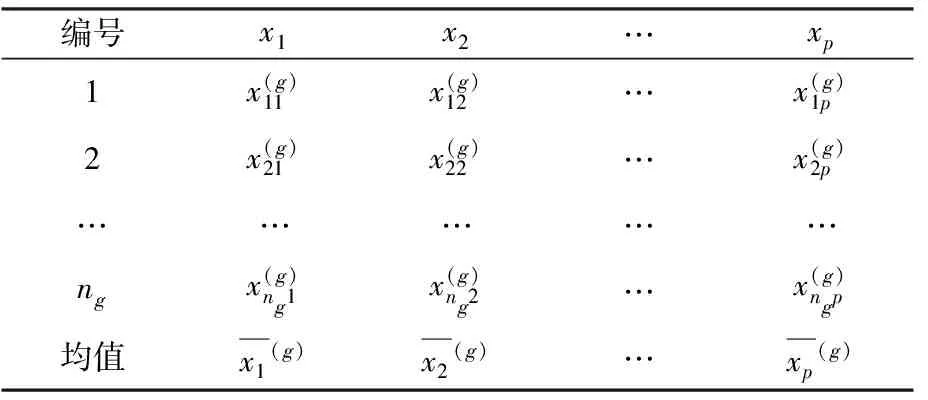
表2 g類訓(xùn)練樣本

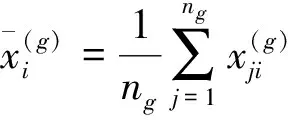
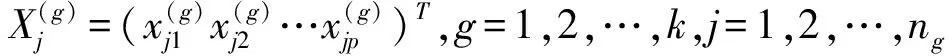
(2)建立判別函數(shù)

1)計(jì)算各類均值及協(xié)方差陣

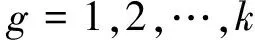
(11)

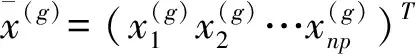
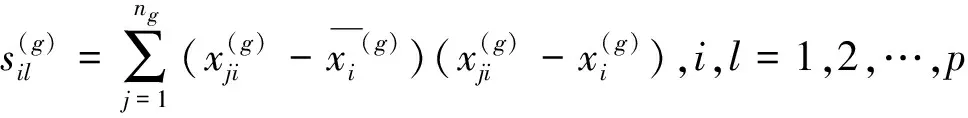
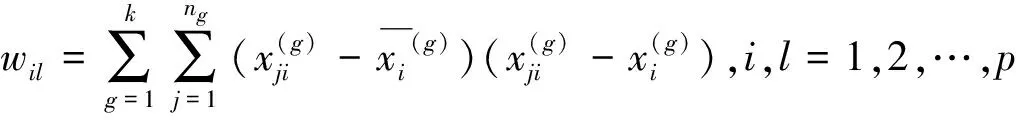
(12)

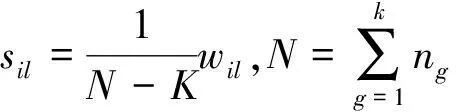
2)判別系數(shù)

計(jì)算協(xié)方差陣S的逆矩陣

令

(13)

(14)

其中

(15)

3)建立判別函數(shù)

建立判別函數(shù)如下：

(16)

對(duì)于任一樣X0=(x1,x2,…,xp)，代入式(16)中，得出k個(gè)值，若其中y(g*)(X0)最大，則該個(gè)體X0=(x1,x2,…,xp)屬于g*類(g*=1,2,…,k)。

2.貝葉斯(Bayes)判別模型實(shí)證分析

基于Clementine軟件的貝葉斯判別模型對(duì)信用風(fēng)險(xiǎn)分類預(yù)測(cè)的基本流程如下：

圖4 Bayes訓(xùn)練模型圖

與Logistic回歸模型類似，在進(jìn)行分類預(yù)測(cè)時(shí)如果采用貝葉斯判別，也需要進(jìn)行變量的篩選，將判別能力強(qiáng)的變量挑選出來構(gòu)建判別函數(shù)，即逐步判別分析法,如圖4。其模型收益(Gain)曲線圖如圖5所示：

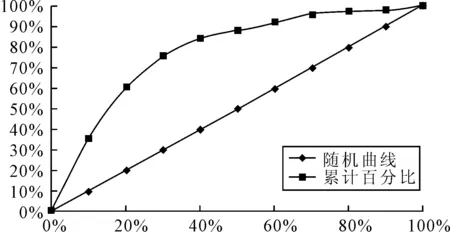
圖5 貝葉斯(Bayes)判別模型收益(Gain)曲線圖

由圖5看出，大約30%的數(shù)據(jù)就可以預(yù)測(cè)出75%的ST類公司(標(biāo)記值為“1”)，分類預(yù)測(cè)的效果較好。從總的預(yù)測(cè)準(zhǔn)確率來看，Logistic回歸模型略好于Bayes判別的結(jié)果，但Bayes判別模型的穩(wěn)健性則略強(qiáng)于Logistic回歸模型。

以上即本文采用的兩種基于統(tǒng)計(jì)方法的分類預(yù)測(cè)模型，這兩種模型均為實(shí)際應(yīng)用中比較成熟的模型，相對(duì)來說，其準(zhǔn)確率和穩(wěn)健性都較好，以下將利用兩種基于數(shù)據(jù)挖掘方法的模型進(jìn)行分類預(yù)測(cè)。

四、基于支持向量機(jī)(SVM)的信用風(fēng)險(xiǎn)分類預(yù)測(cè)模型

1.支持向量機(jī)(SVM)的基本原理

結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則是支持向量機(jī)(SVM)所遵守的主要原則，該方法可以使訓(xùn)練及規(guī)模和VC維之間達(dá)到平衡的狀態(tài)，因此有利于支持向量機(jī)在全局最優(yōu)解這一目標(biāo)實(shí)現(xiàn)的同時(shí)也實(shí)現(xiàn)推廣能力達(dá)到最佳的目標(biāo)。支持向量機(jī)(SVM)的基本思想如下，為保證推廣性的置信范圍以及經(jīng)驗(yàn)風(fēng)險(xiǎn)達(dá)到最小值，同時(shí)實(shí)現(xiàn)對(duì)其的正確分類，從輸入空間非線性將非線性可分?jǐn)?shù)據(jù)集映射到相應(yīng)的高維特征空間，并在該高維特征空間中對(duì)有關(guān)規(guī)劃問題進(jìn)行求解，同時(shí)構(gòu)建出一個(gè)離超平面最近的向量和超平面之間的距離達(dá)到最大的最優(yōu)分類超平面。

2.支持向量機(jī)(SVM)模型實(shí)證分析

基于Clementine軟件的支持向量機(jī)模型對(duì)信用風(fēng)險(xiǎn)分類預(yù)測(cè)的基本流程如圖6、圖7所示：

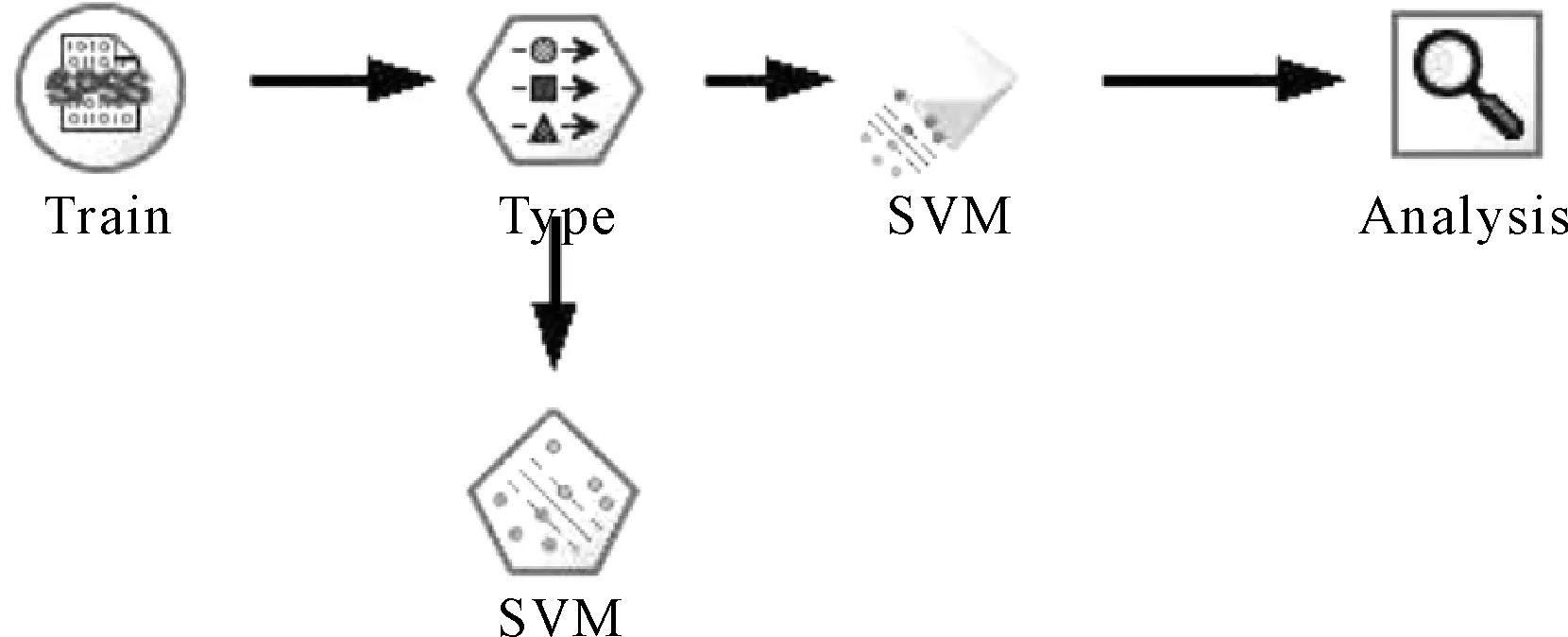
圖6 支持向量機(jī)(SVM)訓(xùn)練模型圖

圖7 支持向量機(jī)(SVM)測(cè)試模型圖

利用10次2-折交叉驗(yàn)證的方法得到的結(jié)果如表3所示：

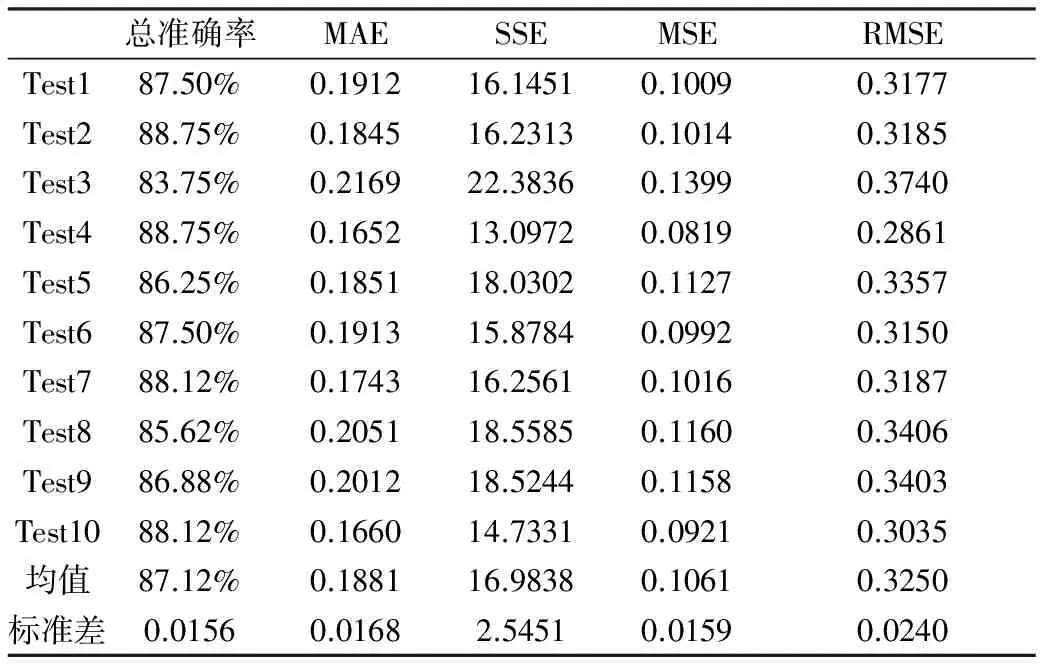
表3 支持向量機(jī)(SVM)模型分類預(yù)測(cè)結(jié)果

其模型收益(Gain)曲線圖如圖8所示：

圖8 SVM模型收益(Gain)曲線圖

通過對(duì)模型結(jié)果的研究能夠看出，該模型的準(zhǔn)確率也比較高，且30%的數(shù)據(jù)就可以預(yù)測(cè)出80%的ST類公司，說明模型效率較高。

以上兩大類模型各有優(yōu)劣，基于統(tǒng)計(jì)方法的模型優(yōu)勢(shì)在于模型的可解釋性較好，從判別方程系數(shù)可以直觀地看出財(cái)務(wù)指標(biāo)的重要程度，同時(shí)，建立在統(tǒng)計(jì)分析基礎(chǔ)之上的模型通常穩(wěn)定性較好，其不足之處在于建模過程中對(duì)樣本要求較高，樣本數(shù)據(jù)的選取對(duì)模型結(jié)果的影響較大。基于數(shù)據(jù)挖掘(或機(jī)器學(xué)習(xí))方法的模型優(yōu)勢(shì)在于模型在訓(xùn)練過程中反復(fù)進(jìn)行迭代，可以達(dá)到較高的預(yù)測(cè)精度，但由于是暗箱操作，只能獲得模型的最終結(jié)果而無法獲知具體各變量的引用情況。

五、結(jié)論

我國(guó)股市大幅崩盤導(dǎo)致大量上市公司違約現(xiàn)象不斷產(chǎn)生，因此使得我國(guó)商業(yè)銀行所面臨的信用風(fēng)險(xiǎn)越來越大，金融業(yè)面臨的最為重要的風(fēng)險(xiǎn)之一即為信用風(fēng)險(xiǎn)，同時(shí)信用風(fēng)險(xiǎn)也是我國(guó)加入世貿(mào)組織之后金融市場(chǎng)所面臨的一個(gè)重大挑戰(zhàn)。基于此，分別利用統(tǒng)計(jì)模型和數(shù)據(jù)挖掘模型進(jìn)行實(shí)證分析，比較各模型自身優(yōu)劣，并進(jìn)行實(shí)證分析和結(jié)果評(píng)價(jià)。在實(shí)際應(yīng)用中，為充分利用這幾類模型的優(yōu)勢(shì)，可以將以上幾種模型進(jìn)行組合，以達(dá)到更好的效果。

[1]陳秀梅,程晗.眾籌融資信用風(fēng)險(xiǎn)分析及管理體系構(gòu)建[J].財(cái)經(jīng)問題研究,2014(12):47-51．

[2]羅方科,陳曉紅.基于Logistic回歸模型的個(gè)人小額貸款信用風(fēng)險(xiǎn)評(píng)估及應(yīng)用[J].財(cái)經(jīng)理論與實(shí)踐,2017,38(1):30-35.

[3]方匡南,范新妍,馬雙鴿.基于網(wǎng)絡(luò)結(jié)構(gòu)Logistic模型的企業(yè)信用風(fēng)險(xiǎn)預(yù)警[J].統(tǒng)計(jì)研究,2016,33(4):50-55.

[4]劉祥東,王未卿.我國(guó)商業(yè)銀行信用風(fēng)險(xiǎn)識(shí)別的多模型比較研究[J].經(jīng)濟(jì)經(jīng)緯,2015,32(6):132-137.

[5]林漢川,張萬軍,楊柳.基于大數(shù)據(jù)的個(gè)人信用風(fēng)險(xiǎn)評(píng)估關(guān)鍵技術(shù)研究[J].管理現(xiàn)代化,2016,36(2):95-97.

[6]丁東洋,周麗莉,劉樂平.貝葉斯方法在信用風(fēng)險(xiǎn)度量中的應(yīng)用研究綜述[J].數(shù)理統(tǒng)計(jì)與管理,2013,32(1):42-56.

[7]史小康,何曉群.個(gè)人信用風(fēng)險(xiǎn)評(píng)分的貝葉斯有偏連接模型研究[J].統(tǒng)計(jì)與信息論壇,2015,v.30;No.173(2):3-8.

[8]鄔建平.基于粗糙集和支持向量機(jī)的電子商務(wù)信用風(fēng)險(xiǎn)分類[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí),2016,46(13):87-92.

[9]隋學(xué)深,喬鵬,丁保利.基于支持向量機(jī)的貸款風(fēng)險(xiǎn)等級(jí)分類真實(shí)性審計(jì)研究[J].審計(jì)研究,2014(3):21-25.

[10]韓兆洲,林少萍,鄭博儒.多類支持向量機(jī)分類技術(shù)及實(shí)證[J].統(tǒng)計(jì)與決策,2015(19):10-13.

責(zé)任編輯：周小梅

2017-05-28

鄒柏松(1987-)，男，湖北宜昌人，碩士，中級(jí)經(jīng)濟(jì)師，研究方向?yàn)閰^(qū)域經(jīng)濟(jì)學(xué)。

TM417

A

1009-1890(2017)02-0016-05