基于直接微分法的水下結構聲學快速敏感度分析

陳磊磊， 趙文暢， 陳海波， 肖琪聃

(1.信陽師范學院 土木工程學院，河南 信陽 464000； 2.中國科學技術大學 近代力學系，合肥 230026)

基于直接微分法的水下結構聲學快速敏感度分析

陳磊磊1， 趙文暢2， 陳海波2， 肖琪聃1

(1.信陽師范學院 土木工程學院，河南 信陽 464000； 2.中國科學技術大學 近代力學系，合肥 230026)

在降低結構振動噪聲方面，結構聲學優化方法展現了很高的應用潛力，并越來越受到研究者們的重視。通過結構聲學敏感度分析建立輻射聲場與結構材料屬性和結構形狀參數的關系，結合優化算法可設計出低輻射噪聲和高聲隱身性能的水下航行結構。發展耦合有限元法與快速多極高階非連續邊界元法進行流固耦合問題的敏感度分析，克服傳統耦合算法的計算精度低，內存占有量高，難以進行大規模實際問題的計算等問題。設計變量可選為流體密度、結構密度、泊松比、楊氏模量、殼厚度和形狀參數等。針對不同設計變量，采用直接微分法分別推導出結構聲學系統和輻射聲功率敏感度表達式。通過帶有解析解的水下點激勵球殼算例驗證算法的正確性與有效性，并通過簡化潛艇算例展示該算法在大規模實際問題上的應用潛力。

輻射聲功率；敏感度分析；耦合有限元與邊界元；非連續邊界元

水中航行結構振動輻射噪聲不僅影響結構內部人員的身心健康，也對海底生物造成干擾。降低振動噪聲和提高水下結構的聲隱身性能是一項非常重要的研究課題。進行水中結構(尤其是薄殼結構)的振動響應分析，流體附加作用不可忽略，同時也增加了數值計算的難度。考慮到有限元在結構振動響應分析和邊界元在無限域外聲場分析時的各自優點，國內外許多學者采用耦合有限元與邊界元方法(FE/BE)進行流固耦合分析[1-4]。然而現有研究大多采用傳統邊界元進行聲場分析，計算量大，內存占有量高，難以進行大規模實際問題的數值計算。文獻[5-6]使用快速多極算法(Fast Multipole Method,FMM)加速流體邊界元計算，提高了流固耦合問題的計算效率，降低了內存占有量。然而這些研究大多采用常量邊界元進行聲場計算，為了提高計算精度，加大結構離散，導致新的計算困難產生。相對于已經被廣泛使用的連續線性和二次邊界元，高階非連續邊界元不僅計算精度高而且避免處理角點問題，尤其在耦合系數矩陣、濕表面面積陣及其逆矩陣的計算上，更加簡單和有效[7]。本文結合高階非連續邊界元與快速多極算法形成快速多極高階非連續邊界元進行結構聲學計算，提高傳統耦合算法的計算精度和計算效率。另外使用單Helmholtz邊界積分方程進行外聲場計算時，會產生解的非唯一性問題，本文使用Burton-Miller方法克服這一問題[8]。

通過敏感度分析研究水中振動結構輻射聲場與結構本身的材料屬性和形狀參數的關系，可指導結構材料的選取和形狀設計，以降低輻射噪聲和提高水下結構的聲隱身性能。文獻[9-10]使用快速多極邊界元法進行聲學敏感度分析，沒有考慮聲振耦合，文獻[11]采用耦合FEM/BEM(Boundary Element Method)方法進行聲振耦合計算，然而在進行敏感度分析時忽略了耦合作用。實際上對聲振耦合方程進行敏感度分析是非常困難的，既要進行結構有限元敏感度計算，又要進行聲學邊界元敏感度計算，同時還需考慮耦合矩陣的敏感度結果，因此現有研究很少進行考慮聲振耦合的敏感度分析。本文克服這些困難，對此進行深入研究，推導出結構聲學耦合敏感度表達式，設計變量可選取為流體密度、結構密度、泊松比、楊氏模量和形狀尺寸參數等。針對不同設計變量分別推導出結構振動輻射聲功率敏感度表達式，進而找到目標函數與設計變量的對應關系，為基于敏感度分析的結構聲學優化設計奠定基礎。最后使用帶有解析解的簡單算法驗證本文算法的正確性和有效性，使用簡化潛艇模型展現本文算法在大規模實際問題中的應用潛力。

1 結構聲學耦合系統

1.1 水下結構聲學系統

組合水下結構振動有限元方程與流體邊界元方程得到表達式

(1)

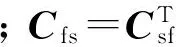
對于實際工程問題，直接求解式(1)，可得到位移響應u和聲壓響應p，然而計算量和內存占有量非常大，難以收斂，并且計算精度不高。為了提高耦合算法的計算效率，將式(1)中的結構振動有限元方程代入到流體邊界元方程中，形成耦合邊界元表達式[7]

Hp-GWCsfp=pi+GWfs

(2)

其中，

W=ω2ρfS-1CfsD-1

D=K-ω2M+iωC

(3)

觀察式(2)發現存在D-1項，實際上直接求解結構矩陣的逆是非常耗時的，本文在計算式(2)右邊D-1fs時，先通過求解線性系統方程Dx=fs，得到x向量即為D-1fs的結果。另外，本文使用GMRES迭代方法求解式(2)，假設第k次迭代步對應的節點聲壓向量為pk,在計算式(2)左邊D-1Csfpk時，先計算Csfpk=b，然后通過求解線性系統方程Dx=b獲得x向量以得到D-1Csfpk的結果。在每次迭代過程中該系統方程都需要被重新求解，由于D矩陣是稀疏帶狀的，使用稀疏直接求解器(Sparse Direct Solver)能十分有效且精確地求解這一系統方程。實際上在每次迭代計算中最耗時的是式(2)的求解，如果使用傳統邊界元算法進行該方程的求解，對于N自由度問題(流體邊界元自由度為N)，計算復雜度為O(N2)，內存占有量也為O(N2)，這無疑是非常耗時和耗內存的，限制了該方法在大規模實際問題中的應用。本文采用寬頻快速多極算法加速傳統邊界元算法中的矩陣向量相乘，同時避免計算流體邊界元系數矩陣G與H，對于N自由度問題，計算復雜度為O(N)，內存占有量也為O(N)，降低了計算量和內存占有量，推進了耦合有限元與邊界元法在大規模實際問題中的應用。

1.2 水下結構聲學系統敏感度分析

在進行敏感度分析時，首先需要確定設計變量，本文針對不同設計變量，例如流體密度、結構密度、泊松比、楊氏模量、結構形狀尺寸等，分別給出相應的敏感度計算表達式。在下面的計算過程中，v代表設計變量。

(1) 當選取流體密度ρf為設計變量，直接將式(2)對設計變量ρf進行微分，可得到如下敏感度表達式

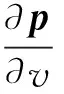
(4)

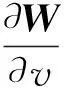
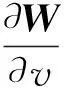
(3) 當選取結構形狀參數為設計變量，直接將式(2)對設計變量進行微分，可得

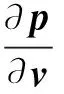
(5)

a=WCsfp+Wfs

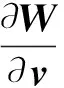
(6)

使用式(2)得到節點聲壓向量值p，然后利用式(4)或式(5)可以得到節點聲壓向量敏感度值。觀察式(6)可發現存在D矩陣求逆后再求導的計算，實際上直接計算D-1已經是十分耗時的，再求導更是非常困難和耗時。為了避免直接計算D-1的導數，本文推導出如下表達式來代替D-1的導數

(7)

本文采用有限差分法來計算式(7)中的D的導數項，設定的有限差分步長為10-4。如果使用傳統邊界元方法進行數值計算，會形成系數矩陣G與H，采用有限差分法可以得到其敏感度結果，然而正如前文所說，該方法計算效率低，實際上對于G或H的敏感度矩陣與向量的相乘，類似于G或H與向量的相乘，可以使用快速多極算法進行加速計算，無需直接計算G、H及其敏感度矩陣，提高了計算效率，降低了內存占有量，為大規模實際耦合問題的敏感度計算及其優化分析提供了有效的數值方法。

使用邊界元法可得到流體域內任一點處的聲壓p

(8)

式中：G(x,y)=iρfωeikr/(4πr);F(x,y)為G(x,y)在點x處的法向導數值;y為域內計算點;S為流固耦合面;r為點x與y的距離。使用式(8)可以得到流體域內任意點處的聲壓值，將式(8)對設計變量進行微分，可得到流體域內任意點處的聲壓敏感度值。

1.3 水下結構振動輻射聲功率的敏感度計算

在流體中，圍繞振動結構的任意面上的輻射聲功率表達式為

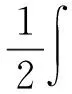
(9)

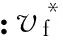
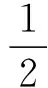
(10)

式中，v為流固耦合面上流體法向速度向量，與結構節點位移向量u具有如下轉換關系

v=-iωS-1Cfsu

(11)

使用式(2)得到節點聲壓向量p，然后利用式(1)中的第一式(結構有限元方程)，得到結構節點位移響應u，最后將式(11)代入到式(10)中，即可得到流固耦合面上的結構振動輻射聲功率。

將式(10)對設計變量進行微分得到如下表達式

(12)

(13)

式中:()H為向量取共軛后再轉置;w1與w2表達式為

w1=iωCfsu*

(14)

耦合系數矩陣Cfs由結構形狀參數決定，與流體密度、結構材料屬性等參數沒有關系。因此，當結構形狀參數被選為設計變量時，Cfs的導數值存在，否則為0。利用式(4)或式(5)可以得到節點聲壓向量敏感度值，為了得到輻射聲功率的敏感度值，還需計算得到節點位移的敏感度值，下面針對不同設計變量，分別推導出u的敏感度表達式。

(1) 當選取流體密度ρf為設計變量，直接將式(1)中的第一式對設計變量ρf進行微分，可得到如下敏感度表達式

(15)

(2) 當選取結構密度ρs、泊松比v、楊氏模量E、殼厚度等參數為設計變量時，得到

(16)

(3) 當選取結構形狀參數為設計變量時(例如球殼半徑)，得到

(17)

使用式(15)～式(17)可以得到節點位移敏感度值，然后利用式(12)即可得到輻射聲功率敏感度值。

2 數值算例

2.1 數值計算離散單元

在數值計算中，先使用有限元軟件ANSYS建立和離散結構模型，導出每個單元的剛度、質量矩陣，然后使用一維變帶寬存儲方法進行所有單元矩陣的整合，最后形成整體剛度和質量矩陣，由于結構矩陣的稀疏與對稱性，只需存儲整體矩陣的上三角非零元素，使用3個一維數組可有效存儲整體矩陣，第一個數組存儲整體矩陣上三角每行非零元素的數量，第二個數組存儲上三角每行非零元素的列編號，第三個數組存儲上三角每行非零元素的值。同時，采用相同網格進行結構有限元與流體邊界元的計算。使用Shell281殼單元進行水下薄殼結構有限元計算，在每個節點處有3個位移自由度和3個旋轉自由度；為了克服傳統連續邊界單元的計算精度低，角點處處理困難等問題，本文使用帶有二次幾何形狀近似的非連續線性邊界單元BE94進行流體邊界元的計算，BE94單元表示使用9節點進行幾何插值計算，使用內部4節點進行物理插值計算，詳細的單元描述和插值過程請參考文獻[7]。

2.2 水下點激勵球殼算例

本節進行水下薄球殼在單點激勵時的振動響應分析，球殼半徑為r，坐標原點在球心處，單位幅值的點激勵作用在點(r,0,0)上，詳細模型圖見文獻[7]，流體與結構參數如表1所示。文獻[7]給出了該模型振動位移響應與輻射聲壓的解析表達式。由于該模型沿X軸軸對稱分布，流固耦合面上的振動輻射聲功率可表達成

(18)

式中:θm=mπ/n;v*f(θm)=iωu*(θm)，足夠大的n能產生高精度的計算結果。將上式對設計變量進行微分可得到輻射聲功率敏感度的解析表達。

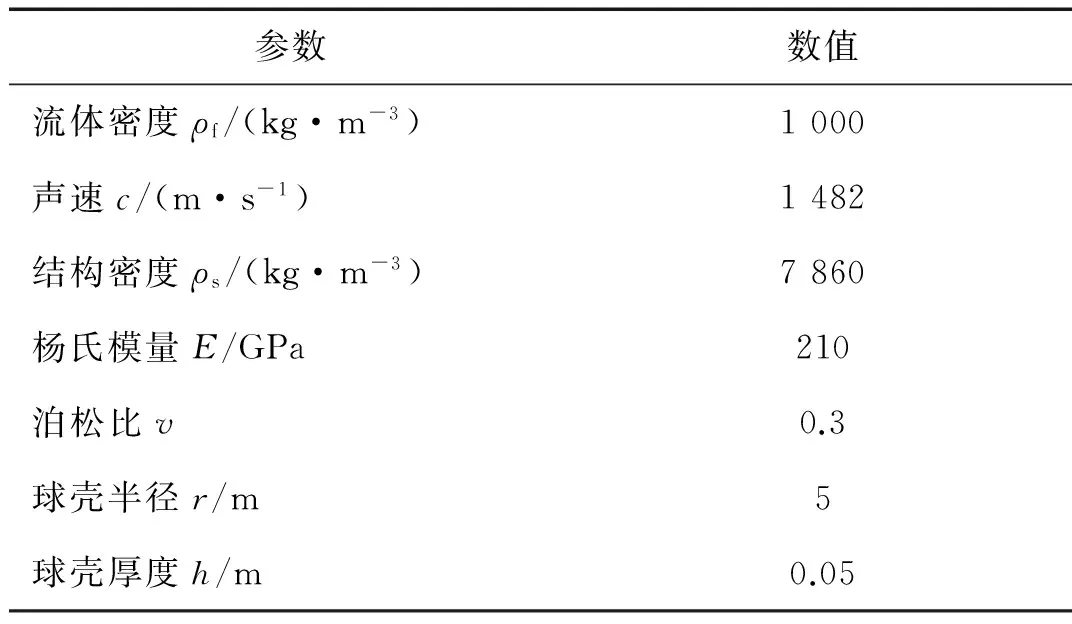
表1 水下球殼的材料與幾何參數

在圖1中，“FE88/FMBE94”表示使用Shell281單元(8節點)進行結構有限元分析，使用帶有二次幾何形狀近似的非連續線性單元BE94進行流體邊界元計算，同時使用FMM算法進行耦合邊界元方程的快速求解。“FE44/FMBE41”表示使用Shell63單元(4節點)進行結構有限元分析，使用帶有線性幾何形狀近似的非連續常量單元BE41進行流體邊界元計算，同時使用FMM算法進行耦合邊界元方程的快速求解。設計變量分別為流體密度和結構密度，計算頻率為50 Hz,計算點分布在距離球心R=2r的圓環上，離散單元數為384。觀察這兩個圖發現，高階耦合單元的計算結果與解析解符合的比較好，然而低階單元的誤差比較大，驗證了本文算法的高精度特點。

(a) 流體密度

(b) 結構密度

Fig.1 Radiated sound pressure sensitivity at distanceR=2rat 50 Hz

在圖2中，后綴“BM”表示使用Burton-Miller方法進行流體邊界元計算，“CBIE”表示使用傳統單Helmholtz邊界積分方程進行流體聲場計算。解析解曲線的計算頻率步長為0.01 Hz，數值解步長為2 Hz，離散單元數為864。觀察該圖可以發現在100 Hz以內的水下結構本征頻率依次為55.9 Hz、70.5 Hz、80.6 Hz、88.4 Hz和94.8 Hz。另外，使用“CBIE”方法在148 Hz左右得到的數值結果偏離解析解，實際上是由于傳統單Helmholtz邊界積分方程在計算外聲場問題時會產生非唯一解的問題，然而使用Burton-Miller法可以有效的解決這個問題。

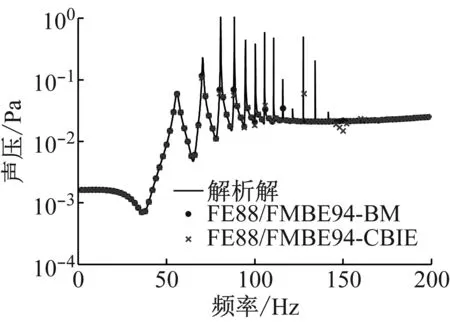
圖2 在點(2r,0,0)處的聲壓隨計算頻率變化圖

圖3呈現了流固耦合面上的輻射聲功率敏感度幅值隨計算頻率變化關系，設計變量依次選取為流體密度、結構密度、泊松比、楊氏模量、球殼厚度和半徑。觀察這些圖可以發現在低頻處敏感度幅值比較小，在結構本征頻率處迅速變化，在一些頻率處急速降低(表現為近似向下垂直線)是由于敏感度值在該頻率附近迅速變化并且發生算法符號的改變，例如由正變負，或由負變正。另外，在這些圖中，數值解與解析解都符合的比較好，驗證了本文算法的正確性和有效性。

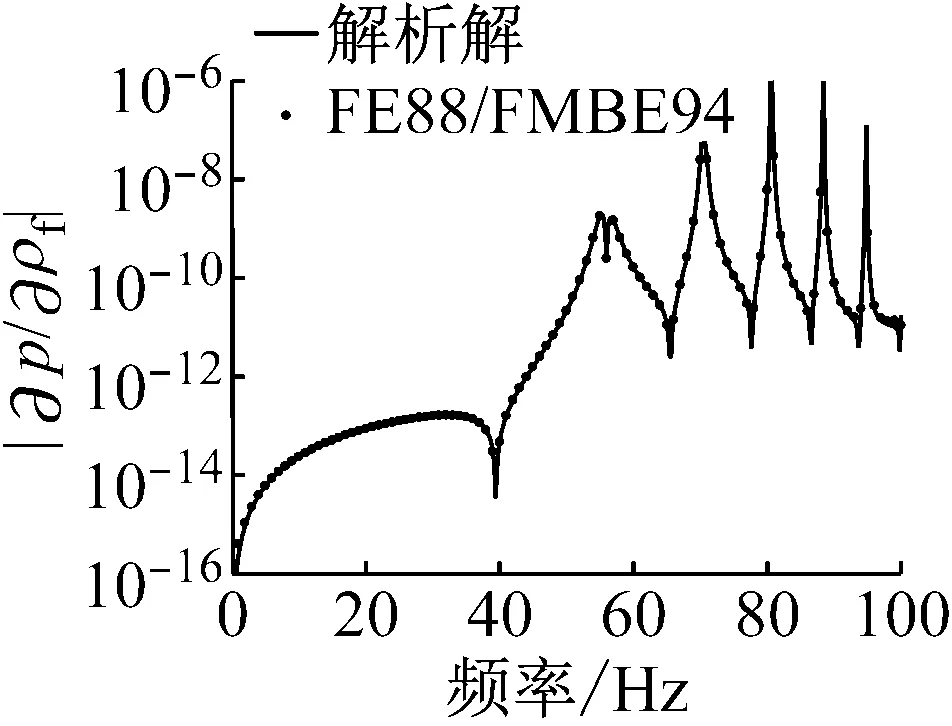
(a) 流體密度

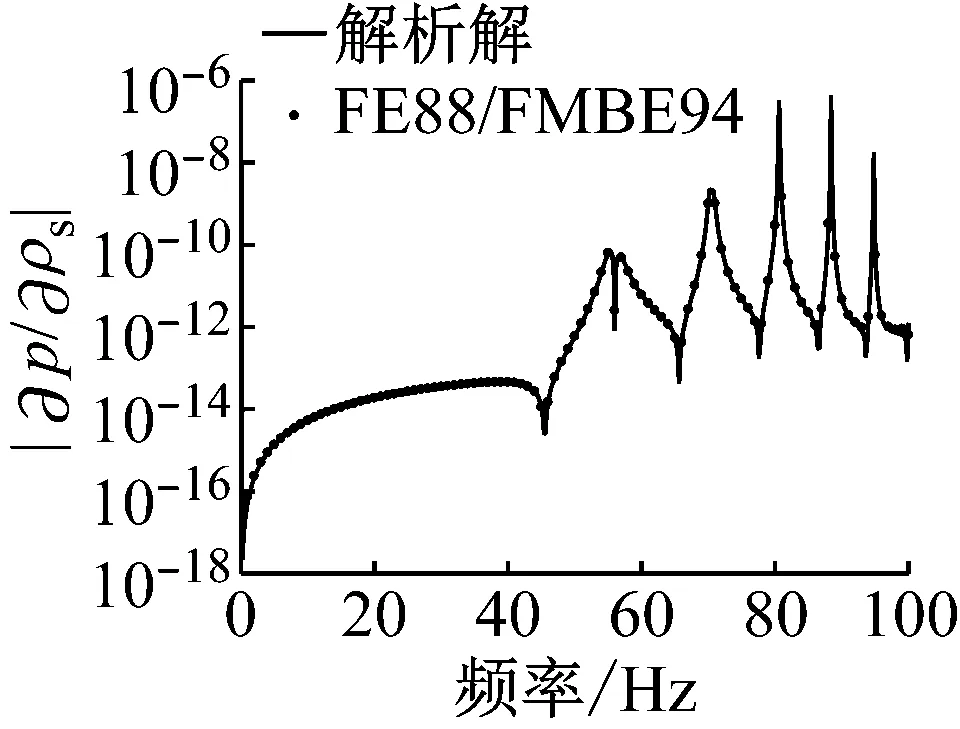
(b) 結構密度

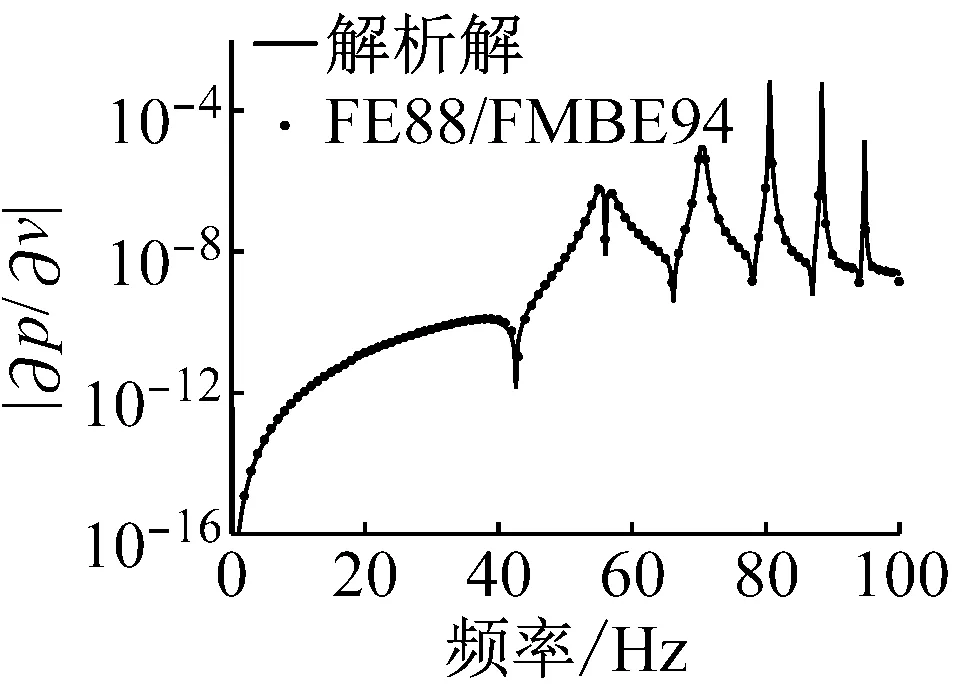
(c) 泊松比

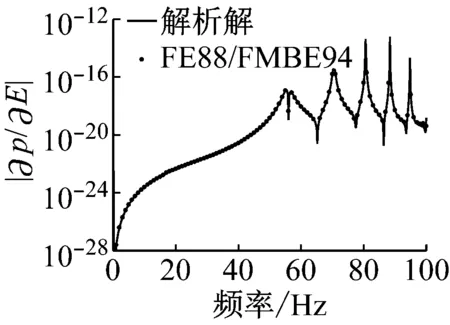
(d) 楊氏模量

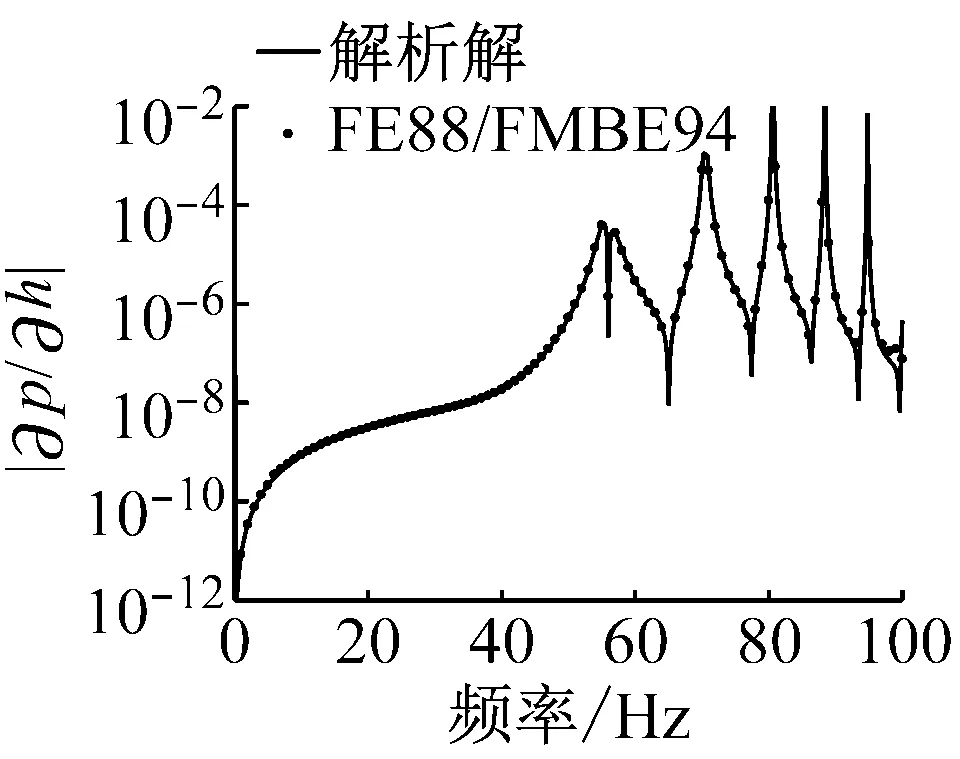
(e) 殼厚度

(f) 球半徑

Fig.3 Amplitude of radiated sound power sensitivity on the fluid-structure interaction surface in terms of frequency

圖4給出了在計算頻率為50 Hz時使用傳統算法與快速算法在計算流固耦合面上的輻射聲功率值時所耗費時間的對比。其中“剛性解”和“加速剛性解”分別表示使用傳統邊界元和寬頻快速多極算法加速計算剛性球模型時所需的時間(不考慮流固耦合)；“彈性解”和“加速彈性解”分別表示使用傳統耦合有限元與邊界元法和耦合有限元與寬頻快速多極邊界元算法計算彈性球模型時所需的時間。由圖4可發現，網格數越多，寬頻快速多極算法的加速效果越明顯。另外，耦合分析比非耦合分析耗費更多時間，這是因為在耦合分析的迭代計算中，每一步都需要求解方程Dx=b，并且彈性耦合的迭代收斂次數遠大于剛性分析次數。

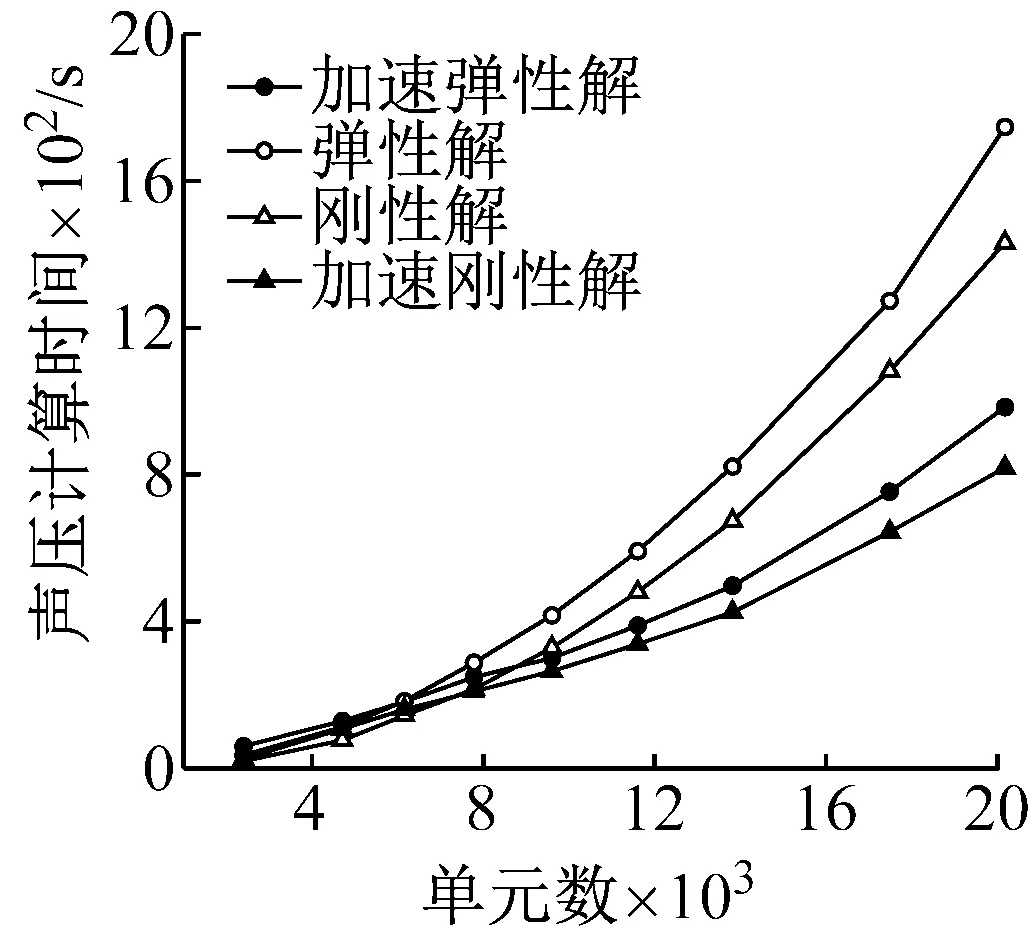
圖4 計算時間隨單元數變化關系

表2給出了采用三種不同類型耦合單元在相近流體邊界節點自由度下(約1 536)計算輻射聲功率時的精度對比，表中的誤差數據表示百分誤差，選取5個頻率進行數值計算。表中“FE44/FMCBE44”表示采用線性有限殼單元(Shell63)進行結構分析，線性連續邊界單元進行聲場分析；“FE88/FMCBE88”表示采用二次有限殼單元(Shell281)進行結構分析，二次連續邊界單元進行聲場分析。觀察表2可以發現FE44/FMCBE44單元表現最差，FE88/FMBE94單元表現最好。另外在80 Hz本征頻率處計算誤差非常大，在200 Hz以外計算誤差隨頻率迅速增加，總之耦合非連續單元表現最好。

表2 三種不同離散耦合單元計算精度對比

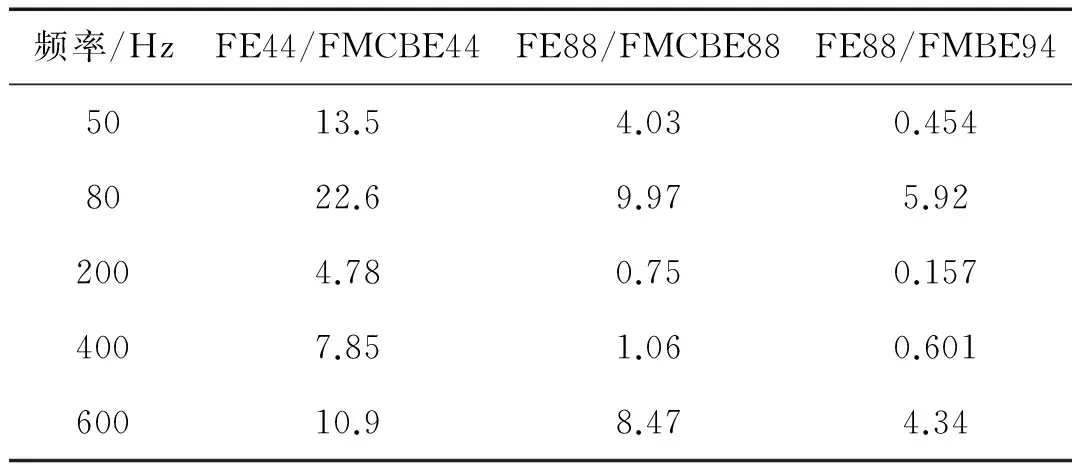
Tab.2 Comparison of calculation accuracy for three different types of coupled elements %

2.3 簡化潛艇結構聲學響應分析

簡化潛艇的形狀與尺寸如圖5所示，分別進行在平面波作用下(沿著正X軸方向傳播，幅值為1 Pa)和在模型兩端的A點與B點處施加集中力F作用下(幅值為1 N)的結構聲學響應分析，流體密度，結構材料屬性參數和殼厚度見表1。

圖5 兩端分別用錐形殼和半球殼封閉的圓柱殼模型

Fig.5 An elastic cylindrical shell with a half-spherical shell and a conical shell

首先進行平面波入射時的聲散射分析。圖6給出了在計算點(-50,0,0)處的聲壓隨計算頻率的變化關系，“剛性解”表明不考慮流固耦合作用，僅采用FMBE94流體單元進行聲學計算，得到流體域內計算點處的聲壓；“彈性解”是采用FE88/FMBE94耦合單元進行流固耦合計算。觀察該圖可以發現，剛性解與數值解的偏差隨著頻率增加而增大，表明進行水下薄殼結果的振動響應分析時必須考慮流體的附加作用。

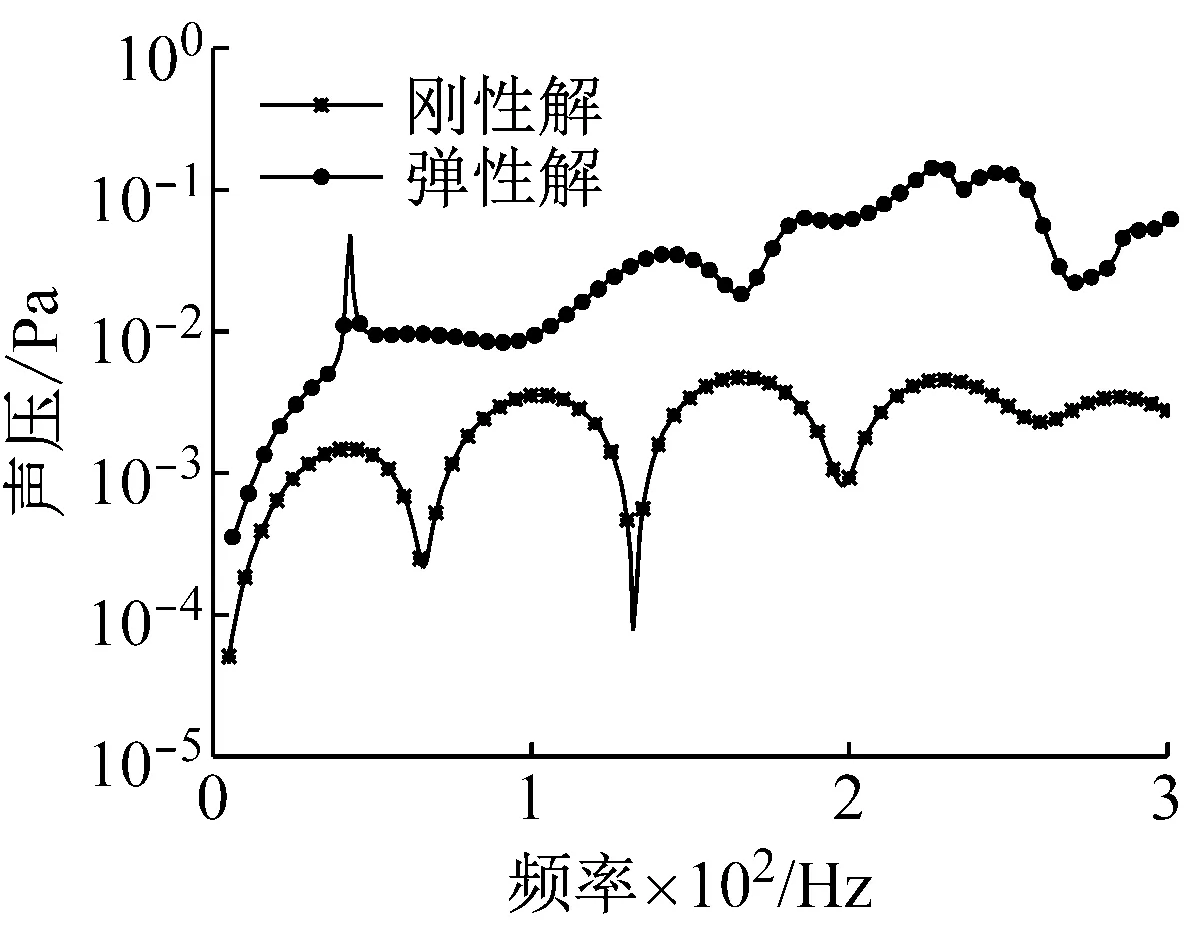
圖6 在計算點(-50,0,0)處的聲壓隨頻率變化圖

Fig.6 Sound pressure at a computing point (-50,0,0) in terms of frequency

圖7呈現了在計算點處聲壓敏感度幅值隨頻率變化關系，殼厚度選為設計變量。使用快速算法得到的計算結果與傳統算法得到的計算結果吻合一致，表明快速算法的使用沒有降低計算精度，保持了傳統邊界元方法的高計算精度優點。另外，在進行平面波作用下的結構散射聲場敏感度計算時，若不考慮流固耦合，只須求解聲學敏感度邊界積分方程，若考慮流固耦合須求解耦合邊界元敏感度方程，增加的計算困難就是耦合矩陣與結構矩陣敏感度的高效求解，尤其當高階耦合單元被使用，更是增加了這一困難。本文使用ANSYS軟件進行結構矩陣的計算，并采用有限差分法計算結構矩陣的敏感度結果。

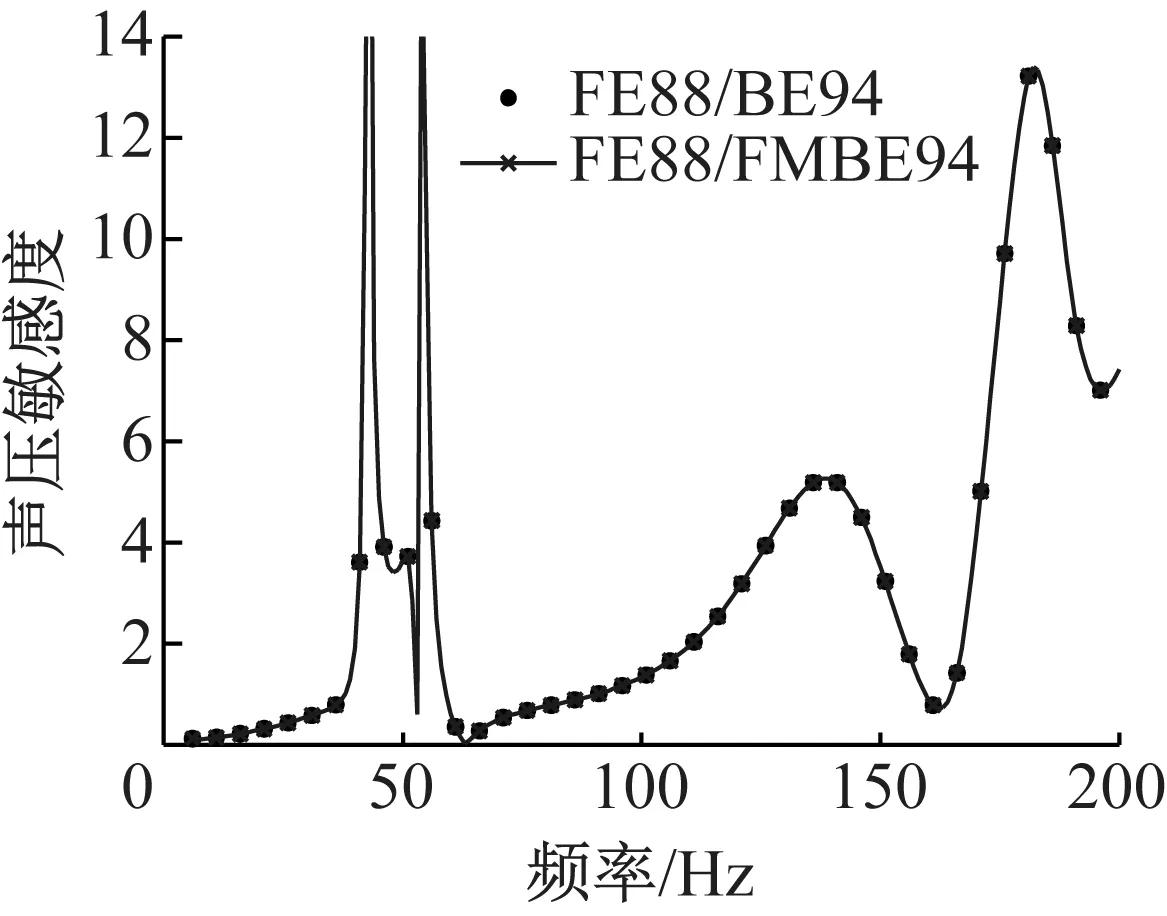
圖7 在計算點處對殼厚度的聲壓敏感度幅值隨頻率變化

Fig.7 Sound pressure sensitivity with respect to the thickness of the shell at the computing point

然后考察在集中力作用下，該模型的振動響應。圖8和圖9分別給出了流固耦合面上的輻射聲功率和其敏感度幅值隨頻率變化關系，設計變量為殼厚度。同樣的，剛性解與彈性解差別很大，實際上結構越薄，耦合影響就越大。

圖8 流固耦合面上輻射聲功率隨頻率變化

Fig.8 Radiated sound power on the fluid-structure interaction surface in terms of frequency

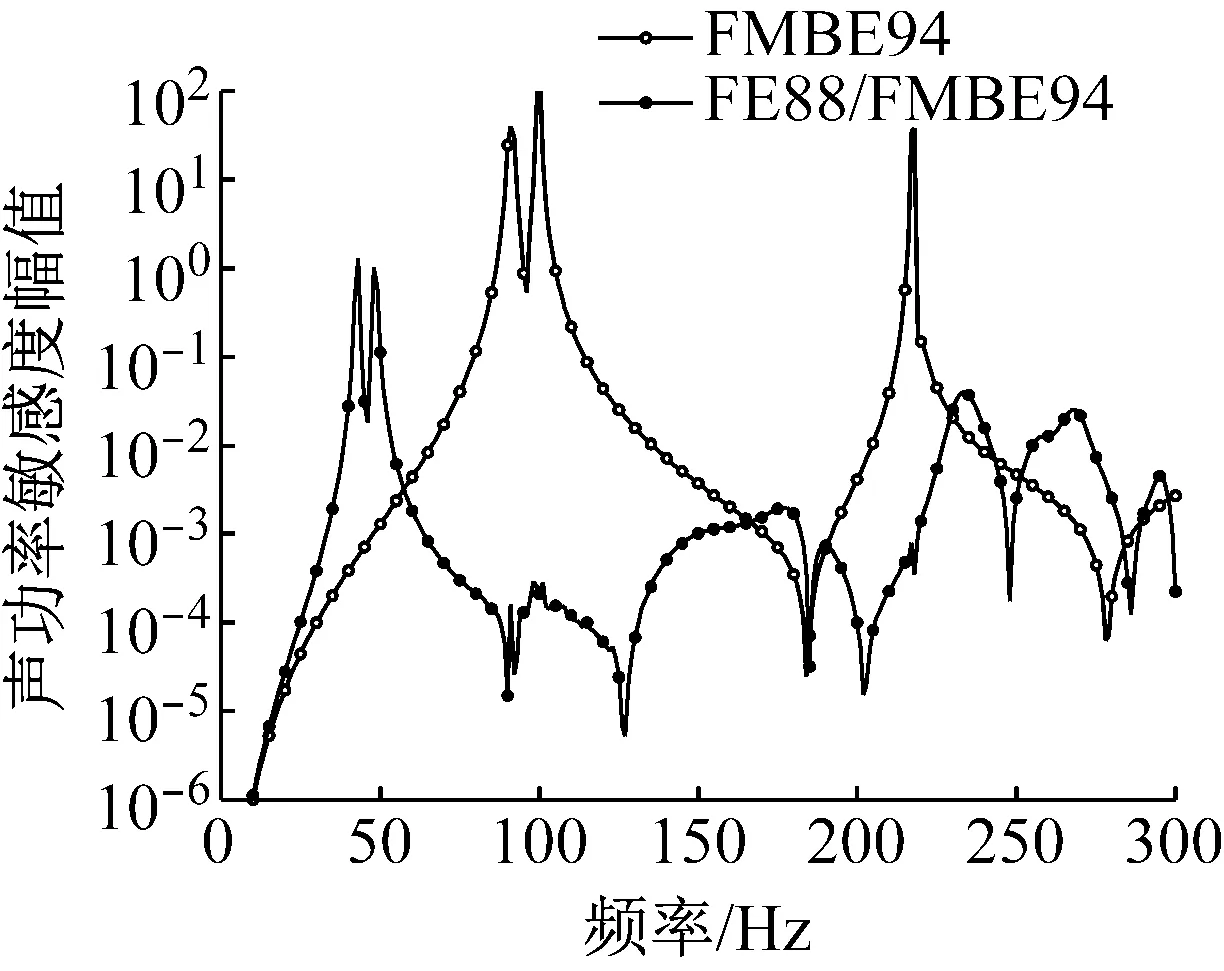
圖9 流固耦合面上輻射聲功率敏感度幅值隨頻率變化

Fig.9 Amplitude of radiated sound power sensitivity on the fluid-structure interaction surface

3 結 論

本文首先推導出用于進行流固耦合分析的耦合邊界元方程和結構振動輻射聲功率表達式，然后針對不同設計變量分別推導出相應的結構聲學敏感度和結構振動輻射聲功率敏感度表達式，通過帶有解析解的點激勵球殼算例驗證本文算法的有效性和正確性，通過簡化潛艇算例驗證本文算法的應用潛力，下一步對整個算法過程與程序編寫進行優化，然后對大規模實際問題進行快速敏感度分析和結構聲學優化算法研究。

[1] 俞孟薩, 史小軍, 陳克勤. 采用有限元和邊界元方法分析彈性加肋圓柱殼的聲學相似性[J]. 中國造船, 1999(3): 65-71.

YU Mengsa, SHI Xiaojun, CHEN Keqin. Study on acoustic similitude of elastic stiffened cylindrical shells by FEM and BEM[J]. Shipbuilding of China, 1999(3): 65-71.

[2] 黎勝, 趙德有.用耦合有限元/邊界元方法研究加筋板的聲傳輸[J].振動工程學報, 2001, 14(3)：364-367.

LI Sheng, ZHAO Deyou. Coupled FEM/BEM approach for analysis of sound transmission through stiffened plates[J].Journal of Vibration Engineering, 2001, 14(3)：364-367.

[3] 沈順根, 李琪華, 王大云, 等. 加肋旋轉殼結構噪聲聲輻射水彈性研究[J].中國造船, 1992(2): 53-62.

SHEN Shungen, LI Qihua, WANG Dayun, et al. Hydroelastic analysis of sound radiation from a stiffened shell of revolution[J]. Shipbuilding of China, 1992(2): 53-62.

[4] ZHENG H, LIU G R, TAO J S. FEM/BEM analysis of diesel piston-slap induced ship hull vibration and underwater noise[J]. Applied Acoustics, 2001, 62(4): 341-58.

[5] 陳磊磊, 陳海波,鄭昌軍,等.基于有限元與寬頻快速多極邊界元的二維流固耦合聲場分析[J].工程力學, 2014, 31(8): 63-69.

CHEN Leilei, CHEN Haibo, ZHENG Changjun, et al. FEM/wideband FMBEM coupling analysis for two dimensional acoustic fluid-strucutre interaction problems[J]. Engineering Mechanics, 2014, 31(8)：63-69.

[6] JUNGE M, BRUNNER D, GAUL L. Solution of FE-BE coupled eigenvalue problems for the prediction of the vibro-acoustic behavior of shipe-like strucutres[J]. International Journal for Numerical Methods in Engineering, 2011, 87: 664-676.

[7] PETERS H, MARBURG S, KESSISSOGLOU N. Structural-acoustic coupling on non-conforming meshes with quadratic shape functions[J]. International Journal for Numerical Methods in Engineering, 2012, 91(1): 27-38.

[8] BURTON A J, MILLER G F. The application of integral equation methods to the numerical solution of some exterior boundary-value problems[J]. Proceedings of the Royal Society of London, 1971, 323: 201-210.

[9] CHEN L L, ZHENG C J, CHEN H B. A wideband FMBEM for 2D acoustic design sensitivity analysis based on direct differentiation method[J]. Computational Mechanics, 2013, 52(3): 631-648.

[10] ZHENG C J, MATSUMOTO T, TAKAHASHI T, et al. A wideband fast multipole boundary element method for three dimensional acoustic shape sensitivity analysis based on direct differentiation method[J]. Engineering Analysis with Boundary Elements, 2012, 36(3): 361-371.

[11] FRITZE D, MARBURG S, HARDTKE H J. FEM-BEM-coupling and structural-acoustic sensitivity analysis for shell geometries[J]. Computers and Structures, 2005, 82(2): 143-154.

Fast analysis for underwater structures’ acoustic sensitivity based on direct differentiation method

CHEN Leilei1, ZHAO Wenchang2, CHEN Haibo2, XIAO Qidan1

(1. School of Civil Engineering, Xinyang Normal University, Xinyang 464000, China；2. Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China)

The structural-acoustic optimization method receives more attention of designers due to its high potential in reducing structures’ vibration and noise. The structural acoustic sensitivity analysis can be used to establish relations among radiated acoustic field, structural material properties and structural shape parameters, then unwater navigating structures with lower radiated noise and higher sound-stealth performance can be designed with the optimization method. Here, the coupled algorithm was developed by combining FE and fast multi-pole higher order discontinuous BE to perform the sensitivity analysis for fluid-structure interaction problems. The developed algorithm improved the calculation accuracy and decreased the memory storage. Fluid density, structural density, Poisson’s ratio, Yong’s modulus, structural shape size and so on were taken as design variables. The sensitivity formulas for structural-acoustic system and radiated sound power with respect to different design variables were derived based on the direct differentiation method, respectively. A numerical example for an underwater spherical shell under a point excitation with an analytical solution was used to verify the validity and correctness of the developed algorithm, and an example for a simplified submarine was used to show the application potential of the developed algorithm in large scale practical problems.

radiated sound power; sensitivity analysis; coupled finite element(FE) and boundary element(BE); discontinuous boundary element(BE)

國家自然科學基金(11172291;U1504505)；河南省科技攻關項目(172102210453)；河南省高等學校重點科研項目(16B560009 ；17A560009)

2016-04-07 修改稿收到日期：2016-05-24

陳磊磊 男，博士，講師，1986年11月生

O39

A

10.13465/j.cnki.jvs.2017.13.026