應用星載GNSS接收機的Molniya軌道衛星測定軌方法

董召勇 尤超藍 李文峰

(上海衛星工程研究所，上海 201109)

?

應用星載GNSS接收機的Molniya軌道衛星測定軌方法

董召勇 尤超藍 李文峰

(上海衛星工程研究所，上海 201109)

針對傳統地基測定軌技術應用于Molniya軌道衛星時跟蹤弧段不足和定位精度低的問題，提出了應用GNSS信息的測定軌方法，以滿足任務對定軌和預報精度要求。分析了Molniya軌道對GNSS星座的導航信息可用性，研究了應用GNSS導航解的軌道確定及預報方法，仿真計算了兩種數據精度模式下導航解作為測量數據參與軌道估算的定軌預報誤差，并分析了測量軌道圈數和跟蹤模型偏差等因素對定軌預報精度的影響。仿真結果表明：利用2圈的導航解參與運算的定軌誤差在15m以內，預報6天的位置誤差在60m以內。此方法具有精度高、穩定性好和數據需求量少等優點，對未來大橢圓軌道衛星測定軌工程實踐具有借鑒意義。

Molniya軌道；全球衛星導航系統；導航解；精密定軌；最小二乘估計

1 引言

Molniya軌道是一種臨界傾角的大橢圓軌道(HEO)，其遠地點位于北半球高緯度地區，遠地點高度和星下點位置較為穩定，具有長期保持在北半球上空的“逗留”特征[1]，1個周期內90%以上的弧段位于北半球上空。Molniya軌道周期通常為12 h，地面軌跡2圈后回歸，在高軌段衛星載荷視場可以完全覆蓋北極地區，廣泛應用于通信、電子偵察和空間物理探測等任務。

目前，針對HEO衛星的測定軌，比較成熟的是采用地基多站測距與測角結合的方式，將地基測量的距離、方位角、俯仰角信息進行批處理后得到初始軌道狀態，進行軌道預報。與天基測量相比，地基測量對衛星軌道的覆蓋率等受地面測控網布設不足的影響十分嚴重，考慮到我國境外測控站部署較少，地基可跟蹤弧段和跟蹤時間受到極大限制。因此，地基測定軌技術應用于HEO衛星的測定軌時，一般定軌精度不高，衛星位置確定精度僅為幾百米。采用星載全球衛星導航系統(GNSS)測定軌技術可克服此不足，并有望實現定軌誤差50 m以內、預報6天誤差100 m以內的能力。

星載GNSS測定軌技術即在衛星上配置GNSS接收機，以導航衛星作為空間基準點測量衛星的位置、速度等軌道狀態信息[2]。出于全球覆蓋的考慮，導航衛星空間部署數量較多，能夠滿足Molniya軌道大弧段覆蓋，在提升測定軌精度的同時，可以實現衛星自主定軌的操作。盡管星載GNSS測定軌技術大多在中低軌道應用，應用于高軌和大橢圓軌道時存在信號“稀疏”等問題，但國內外對其在高軌的應用已進行了積極探索，取得了一定成果。

1997年末，“團隊衛星”(TEAMSAT)/“年輕工程師衛星”(YES)和“赤道衛星”(EQUATOR-S)[3]上的GPS試驗，通過人為地命令接收機去跟蹤特定GPS衛星，成功地在高軌段捕獲到信號；美國空軍研究院主持的Falcon Gold衛星，使用采樣接收機在地球轉移軌道(GTO)上記錄了稀疏的GPS頻譜樣本[4]。這些試驗是衛星在高軌上跟蹤GPS信號的最早案例。

無線電愛好者衛星公司(AMSAT)研制的“AMSAT奧斯卡”衛星(AO-40)[5]運行于HEO軌道，衛星上實施的GPS試驗，表明在高于GPS星座的58 000 km軌道段也可以追蹤到GPS信號，實現無地面介入情況下的全軌段GPS信號自治獲取和跟蹤。在衛星運行速度達10 km/s的低軌段，單個6通道GPS接收機采用簡化的信號獲取方式即可追蹤到4個及以上的GPS衛星。偽距導出的導航解與偽距直接作為測量數據所確定的軌道，兩者之間在3個方向的偏差均值均小于3 km，標準差在幾百米量級。

針對高軌和HEO衛星應用中可見GPS衛星不足而難以獲得導航解的情況，文獻[6]提出了一種HEO軌道確定初始化算法。此算法事先假定標稱軌道根數信息，應用收集的偽距和多普勒測量信息搜索出經過近地點的時間，得到歷元時刻的狀態估計作為濾波初始值，同時提出了一種應用多普勒信息的批處理濾波方法[6]，以計算AO-40衛星的軌道，并成功對無線電愛好者衛星公司的實際飛行數據和戈達德航天飛行中心的飛行仿真數據進行了處理。采用此方法，AO-40衛星沿運行軌跡和垂直運行軌跡方向的位置確定精度分別達到了35 m和87 m。

文獻[7]介紹了一種基于GNSS星間鏈路的中高軌衛星定軌方法，假定用戶衛星也能像導航星座內部中高軌衛星一樣接收GNSS星間鏈路信號，此方法對HEO衛星在徑向的定軌精度可達6 m以內，切向和法向在2 m以內。目前世界主要衛星導航系統中，只有GPS和GLONASS建設有星間鏈路，北斗二號衛星導航系統星間鏈路的建設正在進行。短期內，基于GNSS星間鏈路的測定軌技術難以應用于我國衛星測定軌的工程實踐。

本文提出一種應用GNSS導航信息的Molniya軌道衛星測定軌方法，即將星載GNSS接收機解算出的導航解信息經過批處理濾波改進歷元時刻軌道根數而確定衛星軌道，并實施軌道預報。首先，給出了典型的混合GNSS星座和Molniya衛星軌道的主要參數，并建立了Molniya衛星可利用GNSS信息的限制條件的分析模型，據此計算出用戶星可用GNSS信息的軌道弧段，然后，對Molniya軌道衛星獲取的導航解信息以及軌道確定和預報方法進行了研究，最后，通過仿真算例驗證了方法的可行性。

2 Molniya軌道描述及GNSS星座定義

用戶星運行于Molniya軌道，其軌道根數：半長軸a=26 561.72 km，偏心率e=0.703 403，傾角i=63.4°，近地點幅角ω=270°，升交點赤經Ω=126.091°，平近點角M=0°，初始歷元為2018年7月1日00:00:00(J2000.0)，星下點軌跡如圖1所示。

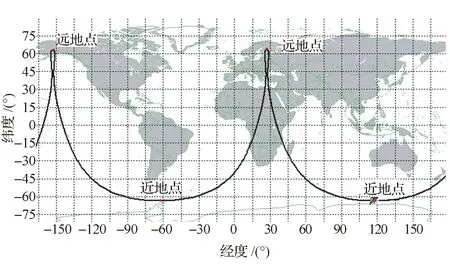
圖1 Molniya軌道星下點軌跡Fig.1 Sub-track of Molniya orbit satellite

導航星運行于混合GNSS星座，星座包含地球靜止軌道(GEO)衛星、傾斜地球同步軌道(IGSO)衛星和中圓地球軌道(MEO)衛星三類衛星。

3 GNSS星座導航信息可用性分析

GNSS接收機在某時刻同時接收到不少于4顆GNSS衛星的信號時，才能夠由偽距測量值求出和用戶星位置相關的導航解，進而認為用戶星在此時刻有“觀測值”(即導航解)。需要開展Molniya軌道

衛星對GNSS星座的導航信息可用性分析，得到用戶星可解算出導航解的軌道弧段。

GNSS系統設計之初主要是針對地面用戶，為其提供連續、實時、高精度的定位導航服務，故GNSS衛星導航信號發射天線主波束指向地球。影響用戶星使用GNSS信息的限制條件[8]有如下4個：

(1)導航星和用戶星之間的幾何視線不被遮擋。

(2)用戶星接收天線在傳輸的GNSS信號主波束范圍內。

Molniya軌道用戶星近地點高度為1500 km，遠地點高度為38 867.2 km，遠地點超過各GNSS衛星的軌道高度，導航星和用戶星的幾何配置如圖2所示，地球遮擋GNSS信號的半錐角為

(1)

式中：Re為地球半徑，rGNSS為地心指向導航星的矢量。

導航星的L1頻段發射天線主瓣波束寬度半角為γ，則約束條件(1)和(2)可抽象為

(2)

式中：ra=-rGNSS，rb=rHEO-rGNSS，rHEO為地心指向用戶星的矢量。

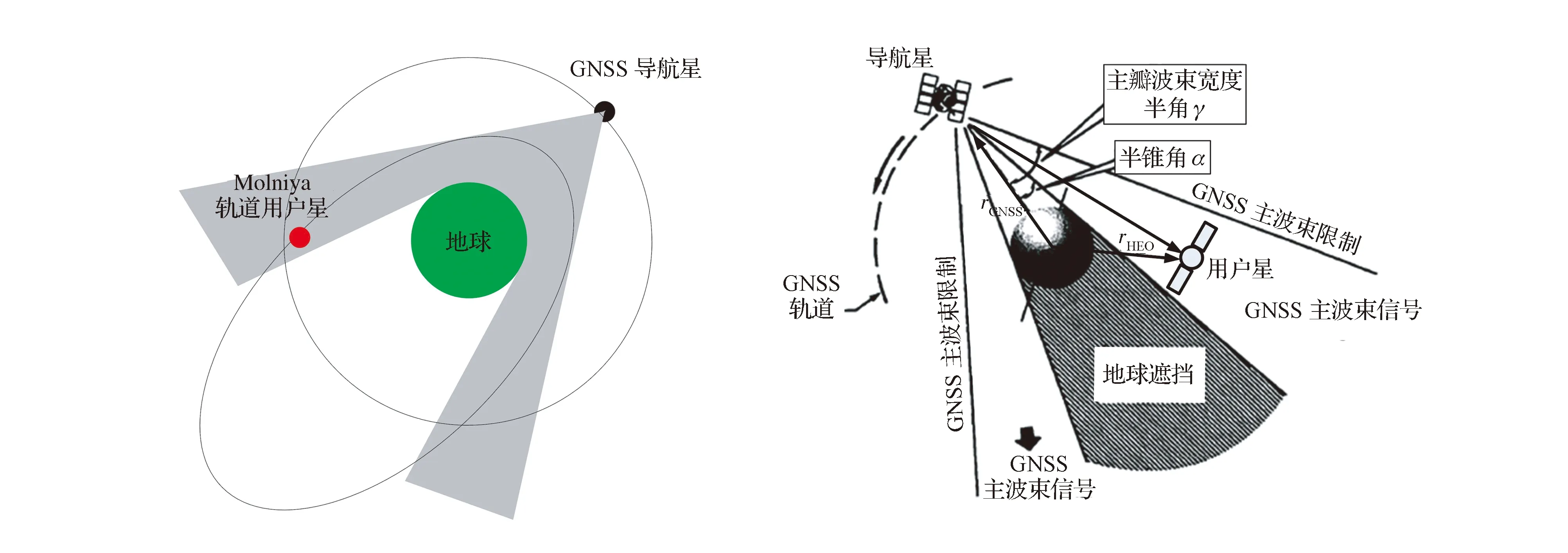
圖2 導航星和用戶星的幾何配置Fig.2 Geometric relationship between navigation satellites and user satellites

(3)用戶星接收到的信號功率超過接收機靈敏度閾值。GNSS接收機接收信號的功率Pr與GNSS衛星發射功率、發射天線增益、鏈路損耗、接收天線增益等諸多因素有關，其計算公式為

(3)

式中：PEIRP為等效各向同性輻射功率，它的定義是衛星天線發送出的功率Pt和該天線增益Gt的乘積，對于GNSS衛星，L1頻段上發射C/A碼的等效各向同性輻射功率為+28.8 dBW；Ld為衛星通信的天波在傳播中受到的自由空間傳播損耗，傳播距離越大，自由空間損耗越大；Gr為GNSS接收天線的增益，一般為3.0 dB；λ為發射信號的波長；R為GNSS衛星到接收機的距離。

接收機靈敏度閾值Pts，目前星載GNSS 接收機中，采用快速傅里葉變換(FFT)的快速捕獲方法，實現了-162 dBW電平下的快速捕獲；在高軌衛星上，GNSS接收機接收到的信號非常微弱，其靈敏度一般較高，為-173 dBW(無星歷)。

則約束條件(3)可抽象為Pr≥Pts。

(4) 剔除衛星數量不夠和相對幾何關系不利弧段，精度衰減因子(DOP)值滿足要求。當可見GNSS衛星數目過少時，用戶星無法通過GNSS星座進行導航定位；當可見GNSS衛星數目足夠多但相對幾何關系較差時，用戶星使用GNSS星座進行導航定位的精度較差。由衛星幾何關系造成的偽距測量與用戶定位誤差間的比例關系，用幾何精度衰減因子DOP來表征，在偽距觀測精度確定的情況下，需要盡可能減小精度因子的數值，以提升對用戶星的定位精度。星座DOP值是影響測量精度的一個重要因素，本文作為仿真研究僅考慮可見GNSS衛星數目的影響，而暫不考慮衛星相對幾何的影響。

4 GNSS接收機獲取的信息及軌道確定與預報方法

根據接收到的4顆或者更多導航星給出的原始偽距測量值，Molniya軌道衛星搭載的GNSS接收機可解算出用戶星的空間位置ru和時鐘偏移量tu，具體解算過程見文獻[9]。導航解即為GNSS接收機解算出的用戶星空間位置，文獻[10]指出，導航解實際上可用作偽測量值進行衛星軌道確定，采用導航解而不是偽距的內在優勢是其簡單的測量模型。針對文章提出的方法，建立了攝動衛星軌道動力學模型和導航解作為測量值的觀測模型，并給出了基于GNSS導航解的批處理算法。

應用星載GNSS接收機的軌道確定與預報方法將涉及諸多時空參考系，時間參考系[11]包括TAI，UTC，GMST，UT1，TT和GPS時間；所涉及的空間參考系[11]包括國際天球參考系(ICRS)、國際地球參考系(ITRS)、WGS84大地坐標系、軌道平面坐標系和RTN坐標系。

4.1 測量模型

在軌道估計問題中將導航解作為觀測值處理，導航解ru在WGS84參考系表示，與ICRS下衛星位置矢量r的關系為

ru(t)=MU(t)r(t)

(4)

式中：U(t)是考慮歲差、章動、地球自轉和極移的從ICRS到ITRS的轉換矩陣；M為ITRS大地坐標系至WGS84大地坐標系的轉換矩陣。經計算，ITRS和WGS84(G873)只有厘米量級上的誤差，兩大地坐標系之間的差異可忽略不計。

引入的測量誤差通常在RTN坐標系下表述，RTN坐標系坐標原點為衛星質心，R軸為徑向(Radial)，與地心到衛星質心連線方向一致；T軸為橫向(Transverse)，在軌道平面內與R軸垂直，指向衛星運動方向；N軸為軌道正法向(Normal)，和瞬時角動量方向一致，與R軸、T軸成右手系。假設在任一時刻，RTN坐標系原點都固定在密切軌道各點上，根據RTN坐標系定義，得到以下關系：

(5)

式中：uR，uT，uN是RTN坐標系統的坐標軸方向矢量；r(t)和v(t)是衛星在ICRS下的瞬時位置和速度矢量；i，j，k是ICRS的坐標軸方向單位矢量。

因此，從ICRS到RTN坐標系轉換矩陣為

(6)

則導航解所在WGS84參考系到RTN坐標系的轉換矩陣為R[MU(t)]-1。

導航解ru對瞬時位置矢量r的偏導數為

?ru/?r=MU(t)

(7)

導航解ru對瞬時速度矢量v的偏導數為0。

4.2 軌道動力學模型

攝動衛星問題的運動微分方程在ICRS坐標系下描述為

(8)

式中：μ為地球引力常數；r為慣性系下衛星相對地球質心的位置矢量；f為單位質量的攝動力，包括地球非球形引力攝動、日月引力攝動、太陽光壓攝動和大氣阻力。Molniya軌道衛星大部分時間處于軌道高度12 000km以上的中高軌段，對衛星軌道影響量級大于10-10km/s2的攝動力僅包括：地球引力場J2,0項攝動、月球引力、太陽引力、地球引力場J2,2項攝動和太陽輻射壓(按量級從大到小排序)[11]。盡管衛星近地點高度達到1500 km，大氣阻力量級較小，但是對于Molniya這種大偏心率軌道，大氣阻力的影響不可忽視。由于太陽光壓系數Cr通常無法由材料常數和衛星幾何來精確計算，需要作為狀態參數在軌道運動方程中進行解算。

4.3 數據批處理算法

狀態方程中除地球中心引力項外，還考慮了J2,0、J2,2、日月引力、太陽輻射壓和大氣阻力等攝動，狀態方程表述為

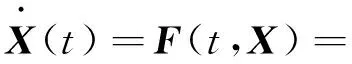
(9)

式中：w(t)為狀態模型誤差，設為獨立零均值的Gauss白噪聲。

觀測方程為

Yi=G(Xi,ti)+εii=1,…,l

(10)

式中：Yi是各離散的觀測時刻ti對應的導航解測量值；v(t)為觀測噪聲，設為獨立零均值的Gauss白噪聲。

待估歷元記為t0，相應的待估狀態量記為X0，x0待估狀態量實際值與參考值之差，借助最小二乘估計的批處理算法進行定軌，可得到歷元時刻x0的估計值為

(11)

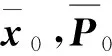
通過軌道確定，一方面得到歷元時刻衛星的精確運動狀態，另一方面將軌道動力學模型描述得更加精準，可以將其用作預報公式，通過數值積分方法推算出任意時刻衛星的運動狀態，以解決GNSS不可用弧段的測軌問題。

5 算例及計算結果分析

假設一種典型的混合GNSS星座進行仿真分析，其組成為：3顆GEO衛星、3顆傾斜地球同步軌道(IGSO)衛星和24顆MEO衛星，合計30顆導航衛星。其中，3顆GEO衛星軌道高度35 788km，分別定點于80°E、110.5°E和140°E；3顆IGSO衛星軌道高度35 788km，傾角55°，星下點軌跡交點分別位于95°E、118°E和147°E附近；24顆MEO衛星軌道高度為20 280km，傾角約55°，近似按照Walker(24/6/1)星座部署于6個軌道面上。各導航衛星星下點軌跡如圖3和圖4所示。

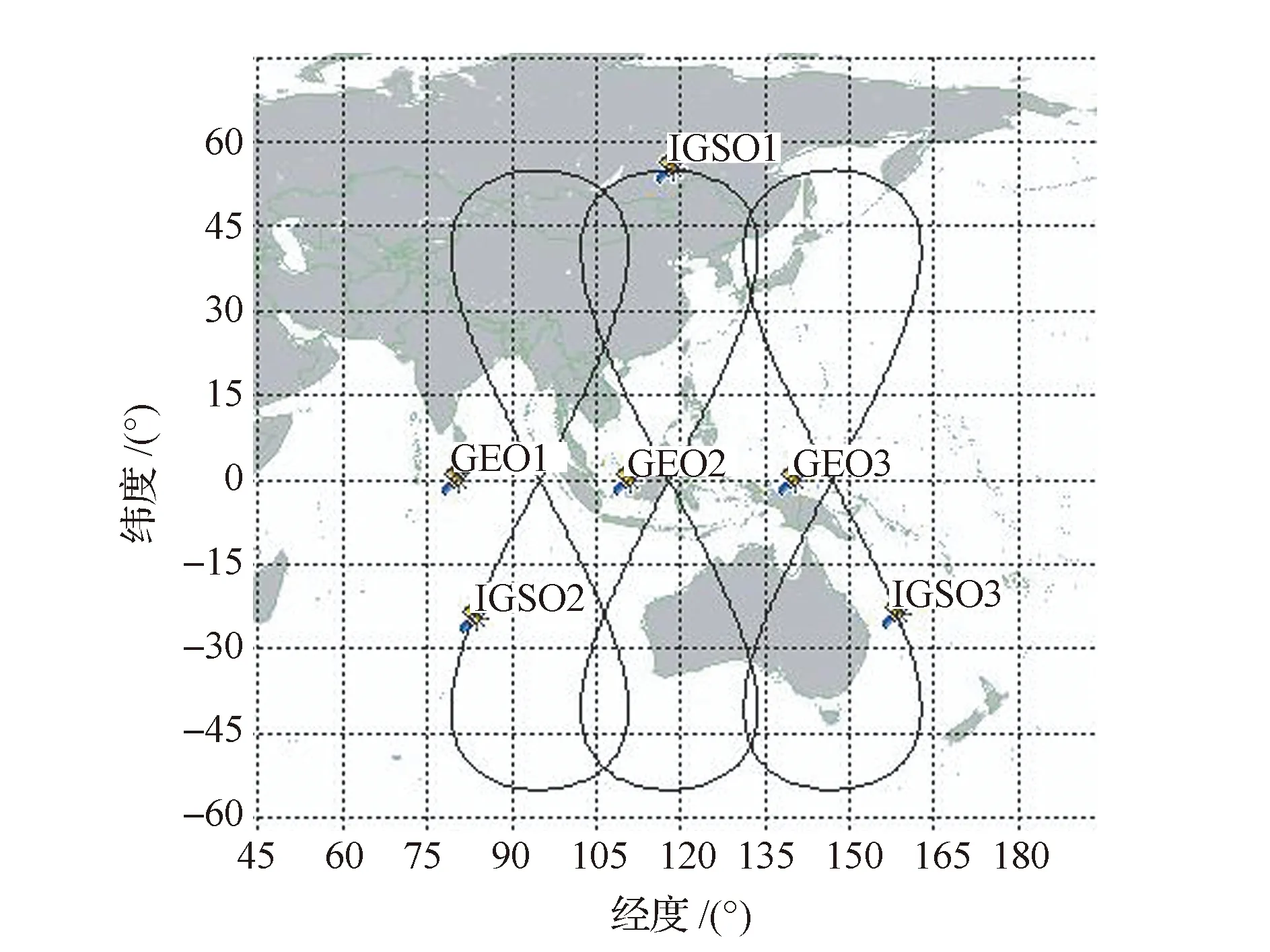
圖3 GEO和IGSO導航衛星星下點軌跡圖Fig.3 Sub-track of GEO and IGSO navigation satellites

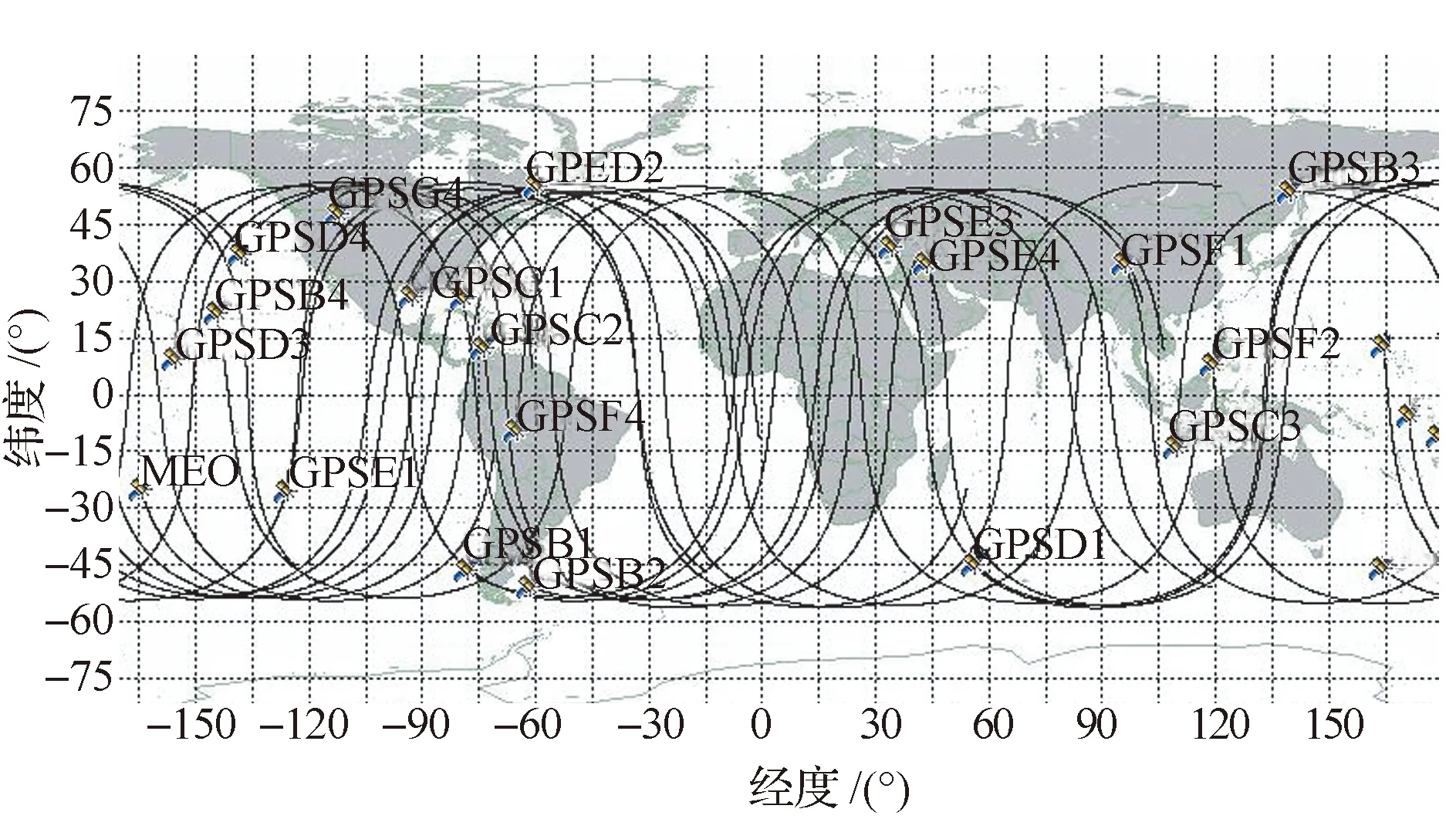
圖4 MEO導航衛星星下點軌跡圖Fig.4 Sub-track of MEO navigation satellites

5.1 導航信息可用性計算

當用戶星可同時獲取4顆及以上的GNSS星信號時，視為在此時刻GNSS信息“可用”。根據軌道特性，各GNSS星和用戶星之間的幾何關系每隔24 h復現一次，只需分析24 h內的情況，就可以推廣到整個用戶壽命周期。圖5是接收機靈敏度分別定為-162 dBW，-173 dBW時GNSS可用衛星數量隨時間的變化情況。

根據圖5可知:

(1)對于所研究的Molniya軌道，可見GNSS星數量≥4顆的弧段集中在軌道高度小于10 000 km的低軌部分；

(2)提高接收機靈敏度可同時增加中高軌及低軌弧段的GNSS可見星的數量；

(3)去除零星的短暫可見部分，接收機靈敏度為-162 dBW時，1天內GNSS信息可用時間為3.03 h，可用弧段如圖6中加粗部分所示；接收機靈敏度提高到-173 dBW時，1天內GNSS信息可用時間增加至4.24 h。

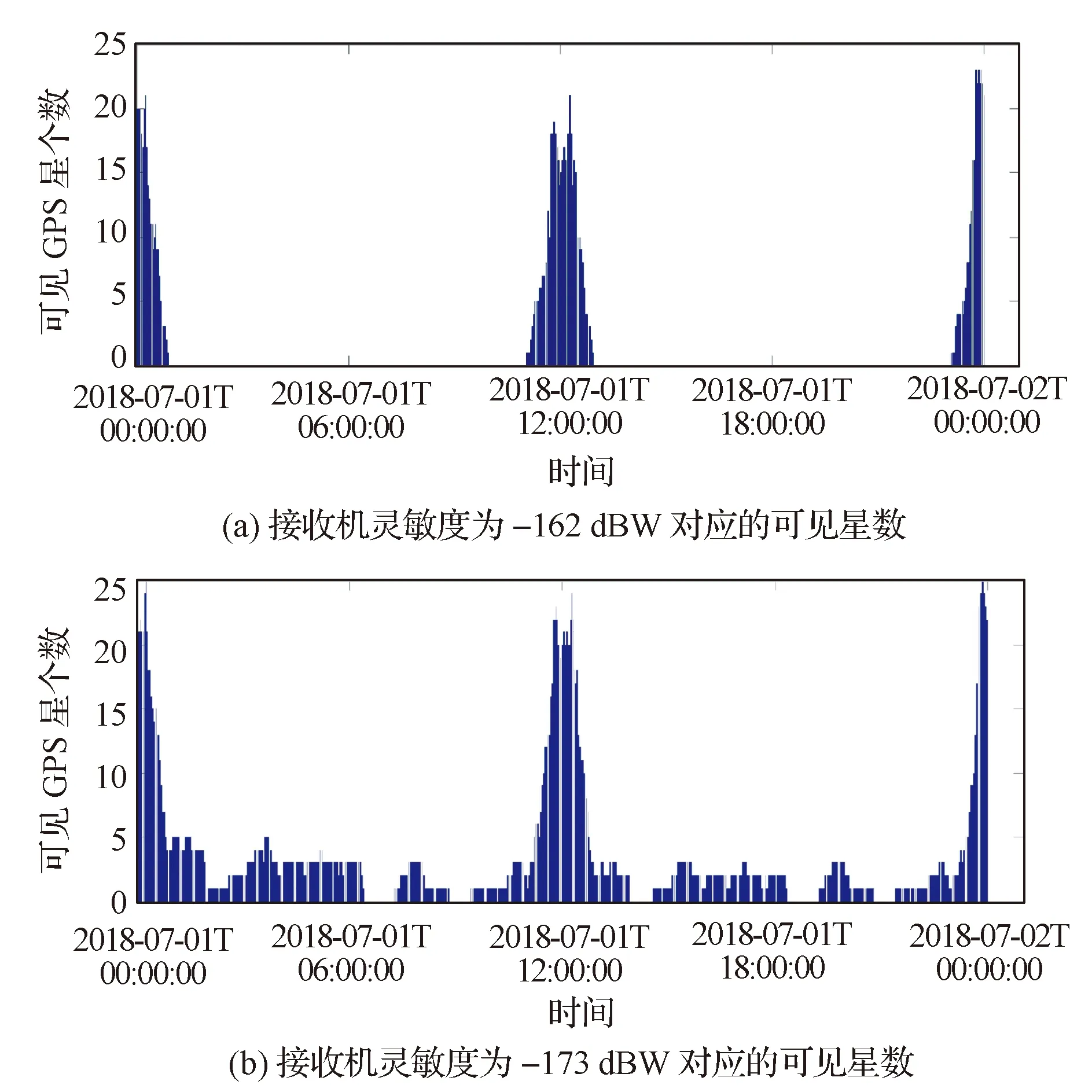
圖5 接收機靈敏度為-162 dBW和-173 dBW對應的GNSS可見星數量Fig.5 Number of visible GNSS stars setting the sensitivity of the receiver as -162 dBW and -173 dBW

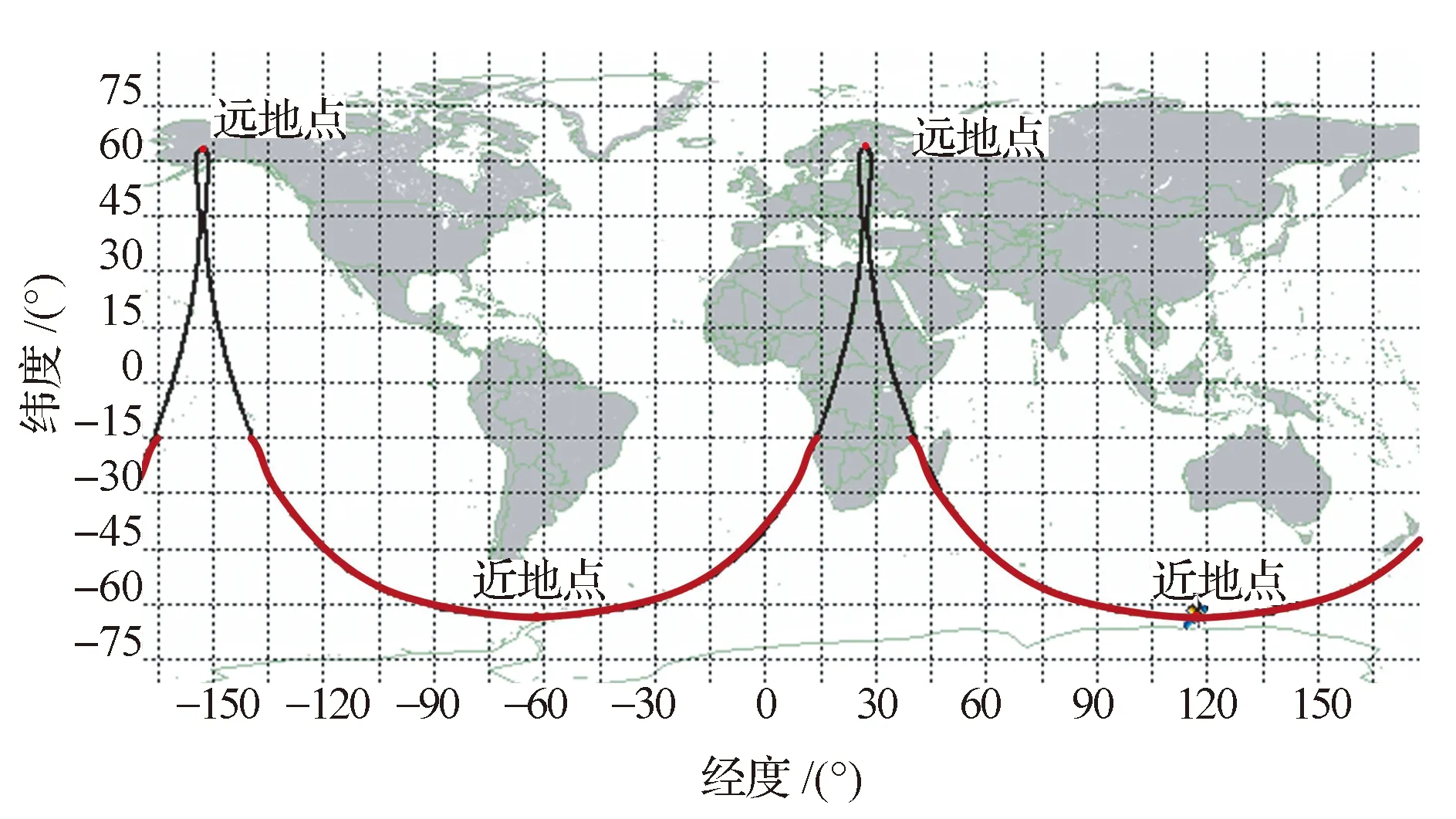
圖6 接收機靈敏度為-162 dBW時對應的GNSS信息可用弧段Fig.6 GNSS information available arcs setting the sensitivity of the receiver as -162 dBW

5.2 定軌預報精度計算

根據GNSS導航信息可用性分析結果，將每圈測量時段設定為：00:00—00:40，11:20—12:00。對于多圈觀測，當前軌道周期的測量時段加上12 h可得下個軌道周期的測量時段，依次類推。每隔60 s取一組數據，一圈可得到80組導航解，利用導航解進行精密定軌計算。

給定兩種導航解精度(WGS84下)：

(1) 對于所有軌道高度的彈道點，3個方向(即RTN坐標系下徑向、橫向和法向，下同)分別添加10 m(3σ)的隨機誤差，簡稱10 m/10 m誤差模式；

(2) 對于距離地面3000 km以下的彈道點，3個方向分別添加10 m(3σ)的隨機誤差；對于3000 km以上的彈道點，3個方向分別添加50 m(3σ)的隨機誤差，簡稱10 m/ 50 m誤差模式。

衛星在軌運行過程中，難以準確獲知其衛星結構、方向和反射系數等信息，光壓攝動的建模會產生偏差。考慮一個存在20%光壓模型偏差(面質比為0.005，光壓系數偏差20%)的動力學模型偏差，參與批處理濾波計算。分別用1圈、2圈、3圈、4圈和5圈的導航解參與批處理濾波計算并預報至第7天，得到表1和表2所示的10 m/10 m和10 m/50 m誤差模式下的定軌預報誤差。

由表1，10 m/10 m誤差模式下，只考慮隨機差而不考慮模型差時，測量圈數超過1時，定軌誤差和預報誤差均可保持2 m以內；同時考慮隨機差和模型差時，隨著測量圈數的增加，定軌誤差從6.87 m逐漸增加至27.61 m，而預報誤差從72.68 m減小至59.68 m后，又逐漸增加至66.89 m。由表2，10 m/50 m誤差模式下，只考慮隨機差而不考慮模型差時，隨著測量圈數的增加，定軌誤差和預報誤差均先減小后增大，保持10 m以內；同時考慮隨機差和模型差時，隨著測量圈數的增加，定軌誤差從13.29 m逐漸增加至27.05 m，而預報誤差基本不變，維持60 m左右，該方法對測量圈數的依賴性不強。需要說明的是，由于測量數據生成時引入的誤差值具有隨機性，本文針對同一種工況多次模擬了數據生成和批處理濾波過程，通過蒙特卡羅仿真分析定軌誤差分布規律。然而，可能因為同一工況模擬仿真次數不足，未能完全規避誤差值的偶然性因素，出現了應用2圈測量數據的定軌和預報精度都略優于3圈的情況。

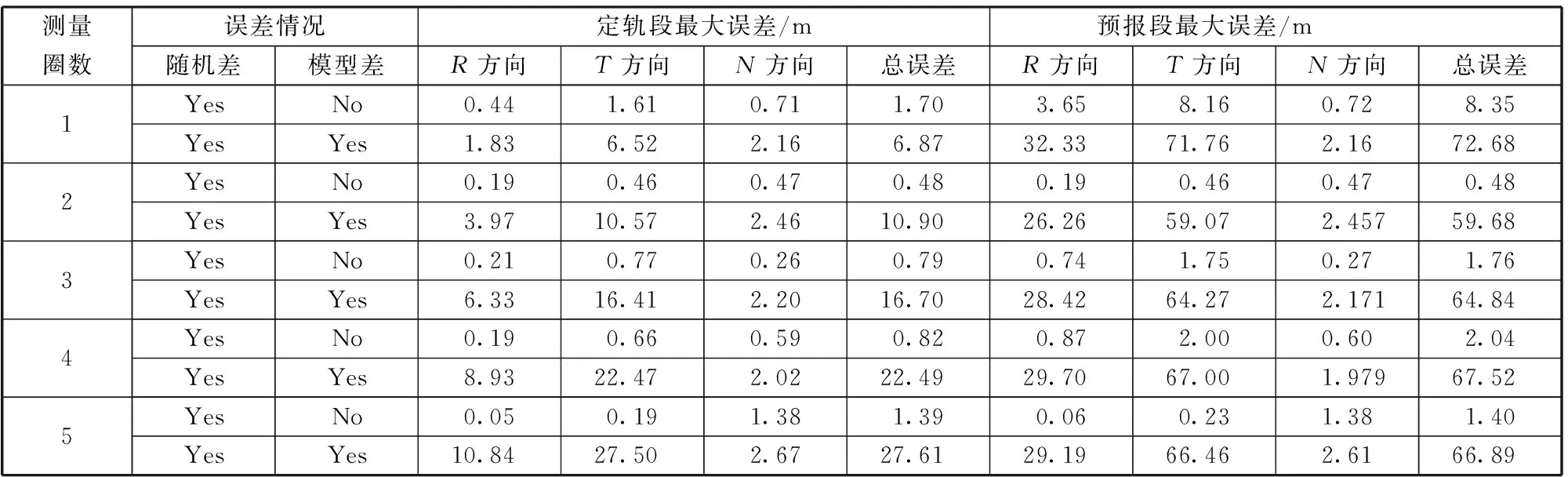
表1 10 m/10 m測量誤差模式下的定軌預報誤差

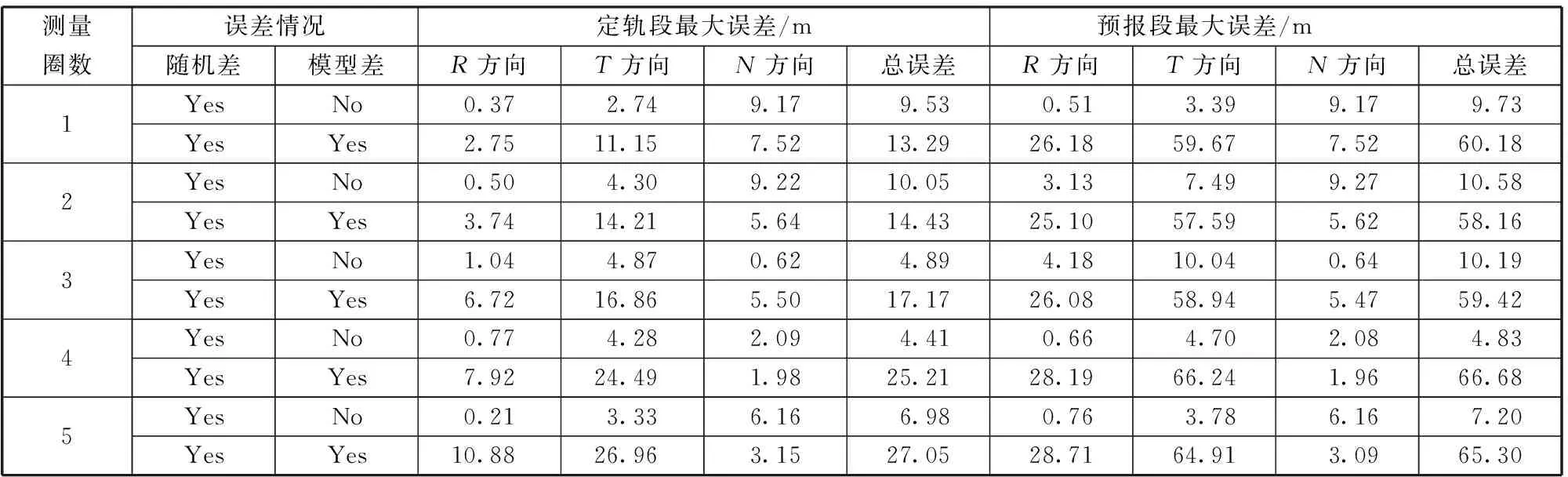
表2 10 m/50 m誤差模式下的定軌預報誤差

比較表1和表2數據，只考慮隨機差而不考慮模型差時，10 m/10 m誤差模式對應的定軌誤差和預報誤差都遠小于10 m/50 m誤差模式對應的值；同時考慮隨機差和模型差時，10 m/10 m和10 m/50 m誤差模式對應的定軌誤差和預報誤差基本相等。測量隨機誤差對定軌預報精度的影響不明顯，模型差的影響比測量誤差顯著。

圖7給出了利用2圈的導航解進行軌道估計計算，兩種誤差模式下的定軌預報誤差曲線。其中，定軌段為0～24 h，預報段為24～168 h。

圖7中，實線表示10 m/10 m誤差模式對應的定軌預報誤差曲線，虛線表示10 m/50 m誤差模式對應的定軌預報誤差曲線。從圖7看出，利用2圈的導航解進行軌道估計計算，兩種誤差模式下的定軌預報誤差在R方向和T方向的變化曲線基本重合，只是在N方向略有差異。

綜上所述，應用星載GNSS的測定軌方法的定軌預報精度對測量圈數的依賴性不強，2圈的GNSS導航解數據即可確保較高的定軌預報精度。引入系統誤差和模型偏差后，定軌預報精度雖略有下降，但不會急劇發散，說明此方法對測量誤差的影響不敏感，穩定性好。利用2圈的導航解參與運算的定軌誤差在15 m以內，預報6天的位置預報誤差在60 m以內，優于傳統地基測定軌方法，滿足任務需求。

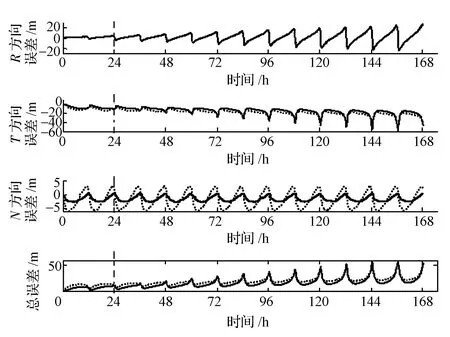
圖7 定軌預報誤差變化曲線Fig.7 Orbit determination and prediction error curve

6 結束語

作為一種大橢圓軌道，Molniya軌道偏心率很大，傳統地基測定軌方法的衛星定軌誤差對測量誤差是極其敏感的，測量數據的微小誤差就能引起定軌預報的較大誤差[12]。應用星載GNSS接收機的測定軌方法將接收機解算出的導航解信息直接作為測量數據進行軌道確定和軌道預報，具有精度高、穩定性好和數據需求量少等優點，實現了衛星自主定軌的操作。與傳統地基測定軌方法相比，定軌預報精度從百米量級提升到了幾十米量級，對測量誤差和模型誤差的敏感性也顯著降低，此方法具有一定的工程參考價值。

References)

[1]Ilcev S D. Highly elliptical orbits (HEO) for high latitudes and polar coverage[C]// 20th International Crimean Conference on Microwave & Telecommunication Technology.New York: IEEE ,2010

[2]樊士偉,孟軼男,高為廣,等. 航天器測定軌技術發展綜述[J]. 測繪科學技術學報,2013,30(6):549-554

Fan Shiwei,Meng Yinan,Gao Weiguang,et al. Summarizing on the development of spacecraft orbit determination technology[J]. Journal of Geometrics Science and Technology,2013,30(6):549-554 (in Chinese)

[3]Balbach O,Eissfeller B,Hein G W,et al. Tracking GPS above GPS satellite altitude: first results of the GPS experiment on the HEO mission equator-S[C]//Position Location and Navigation Symposium. New York: IEEE,1998:243-249

[4]Silva R,Chao C C,Sedlacek S B,et al. GPS signals in a geosynchronous transfer orbit: Falcon Gold data processing[R]. Colorado: United States Air Force Academy,1999

[5]Davis G,Moreau M,Carpenter R,et al. GPS-based navigation and orbit determination for the AMSAT AO-40 satellite[R]. Maryland: Goddard Space Flight Center,2002

[6]Axelrad P,Speed E. Algorithms for autonomous GPS orbit determination and formation flying: investigation of initialization approaches and orbit determination for HEO[R]. Colorado: University of Colorado,2002

[7]孟軼男,樊士偉,李罡,等. 利用GNSS星間鏈路對中高軌航天器測定軌的可行性分析[J]. 武漢大學學報信息科學版,2014,39(4): 445-449

Meng Yinan,Fan Shiwei,Li Gang,et al. Orbit determination of medium-high earth orbital satellite using GNSS crosslink ranging observations[J]. Geomatics and Information Science of Wuhan University,2014,39(4):445-449 (in Chinese)

[8]Li T,Liu J,Huang Z,et al. Observability of HEO satellite autonomous navigation system using GPS[C]// 2010 International Conference on Multimedia Technology. New York: IEEE,2010

[9] Kaplan E D,Hegarty C J. Understanding GPS:principles and applications,2nd edition[M]. London: Artech House,Inc.,2006

[10]Carter S S,Cefolo P J,Proulx R J. The determination of precision mean element sets from GPS receiver on-board navigation solution [C]//Proceedings of the AAS/AIAA Astrodynamics Conference.California: Univelt,Inc.,1995

[11]Montenbruck O,Gill E. Satellite orbits: models,methods,and applications[M]. Berlin: Springer,2000

[12]Antreasian P G,Baird D T,Border J S,et al. 2001 Mars Odyssey orbit determination during interplanetary cruise[J]. Journal of Spacecraft and Rockets,2005,42(2):394-405

(編輯：李多)

Precise Orbit Determination Method of Molniya Orbit Satellites Using Onboard GNSS Receiver

DONG Zhaoyong YOU Chaolan LI Wenfeng

(Shanghai Institute of Satellite Engineering,Shanghai 201109,China)

Considering the problems of lacking visible arc and the low positioning accuracy using the traditional ground-based orbit determination technology,the method using onboard GNSS information is proposed in this paper in order to meet the orbit determination and prediction accuracy from the space mission requirements. The navigation information availability of GNSS constellations is analyzed and the algorithm of orbit determination based on GNSS navigation solutions is studied,then the orbit determination and prediction errors are calculated taking navigation solutions of different accuracy as measurement data. The influence of measured orbital circles and the accuracy of tracking model to orbit determination and prediction accuracy is analyzed. The simulation results show that the orbit determination errors can be restricted below 15 meters and after six days’ prediction the position errors can be restricted below 60 meters using navigation solutions of two orbit circles,when taking the random errors of measurement data and the model deviation into consideration. The method has advantages of high precision,strong stability and low data demand,which may be used for future HEO satellite orbit determination engineering.

Molniya orbit; GNSS; navigation solution; precise orbit determination; least square estimation

2017-04-18；

2017-05-10

董召勇，男，碩士，工程師，研究方向為衛星姿軌控設計。Email：dongzhaoyong1990@163.com。

V

A

10.3969/j.issn.1673-8748.2017.03.004