(2+1)維廣義Calogero-Bogoyavlenskii-Schiff方程的所有單行波解的分類、表示及分叉行為
杜興華
( 東北石油大學 數學與統計學院,黑龍江 大慶 163318 )
(2+1)維廣義Calogero-Bogoyavlenskii-Schiff方程的所有單行波解的分類、表示及分叉行為
杜興華
( 東北石油大學 數學與統計學院,黑龍江 大慶 163318 )
利用多項式完全判別系統法,求出(2+1)維廣義Calogero-Bogoyavlenskii-Schiff方程的所有單行波解的分類和表示(包括新解),顯示參數變化導致的分叉現象,從局域運動轉變到周期波動,體現模型豐富的物理內涵。
多項式完全判別系統; 行波解; 廣義Calogero-Bogoyavlenskii-Schiff方程; 分叉現象
0 引言
求解非線性發展方程的精確行波解是非線性科學中的主要課題,已發展出來反散射法[1]、Backlunud法[2]、Darboux變換法[3]、延拓法[4-5]、Painleve分析法[6]、 Lie群法[7-8]、 Tanh函數法[9]。劉成仕提出多項式完全判別系統法[10-14],即通過化所求方程為初等積分形式,利用多項式完全判別系統構造非線性發展方程的精確行波解,可以求得多種非線性發展方程豐富的精確行波解。對于某些非線性發展方程,可以得到所有單行波解的分類,其中包含其他方法得不到的新解。筆者利用多項式完全判別系統法,研究(2+1)維廣義Calogero-Bogoyavlenskii-Schiff(GCBS)方程[15-17],求出GCBS方程的所有單行波解的分類和表示,其中包含新解,同時討論解的物理意義及物理模型豐富的動力學行為。
1 單行波解分類
考慮(2+1)維廣義Calogero-Bogoyavlenskii-Schiff(GCBS)方程
αuxt+βuxuxz+δuzuxx+uxxxz=0,
(1)
式中:α≠1;β、δ為任意非零常數。
式(1)是由Bogoyavlenskii O I利用Calogero F建議修改的Lax格式構造的,是Schiff J利用約化規范場論中的Yang-Mills方程得到的[18-20]。當令α=4,β=4,δ=2時,式(1)變成Bogoyavlenskii-Schiff方程;當α=4,β=8,δ=4時,式(1)變成(2+1)維Calogero-Bogoyavlenskii-Schiff(CBS)方程。如文獻[15]利用廣義Riccati方程展開法獲得一些精確解;文獻[17]構造無窮序列類孤子新解。
對式(1)做行波變換
u(x,z,t)=u(ξ),ξ=kx+lz-ωt。
(2)
將式(2)代入式(1)得到非線性微分方程
-αkωu″+βk2lu′u″+δk2lu′u″+k3lu(4)=0。
(3)
對式(3)進行關于ξ積分得
?=c1,
(4)
式中:c1為積分常數。
做變換
ν=u′,
(5)
將式(5)代入式(4)并積分得
(6)
式中:c0為積分常數。
做變換
(7)
則式(6)變成
(8)
令
F(w)=w3+d2w2+d1w+d0,
(9)
其中
(10)
將式(8)化為初等積分
(11)
式中:ξ0為積分常數。F(w)完全判別系統為
(12)
根據三階多項式完全判別系統Δ和D,分為四種情形討論。
情形1Δ=0,D<0,F(w)=0有一個二重實根和一個單重實根,即
F(w)=(w-α1)2(w-α2),
(13)
式中:α1、α2為實常數,且α1≠α2。對式(11)進行積分得
(14)
(15)
如果w>α2,則式(6)的精確解為
(16)
(17)
(18)
情形2Δ=0,D=0,F(w)=0有一個三重實根,即
F(w)=(w-α1)3。
(19)
式(6)的精確解為
(20)
情形3Δ>0,D<0,F(w)=0,有三個不同的實根,即
F(w)=(w-α1)(w-α2)(w-α3),
(21)
式中:α3為實常數,且α1<α2<α3。式(12)變為
(22)
當α1 (23) 當w>α3時,式(6)的精確解為 (24) 情形4Δ<0,F(w)=0有一個實根和一對共軛復根,即 F(w)=(w-α1)(w2+pw+q), (25) 式中:p、q為實常數,且p2-4q<0。式(12)變為 (26) 當w>α1時,式(6)的精確解為 (27) 定理 式(1)的所有單行波解的分類: (1)如果ν1(ξ)是式(6)的解,那么式(1)的行波解為 (28) (2)如果ν2(ξ)是式(6)的解,那么式(1)的行波解為 (29) (3)如果ν3(ξ)是式(6)的解,那么式(1)的行波解為 (30) (4)如果ν4(ξ)是式(6)的解,那么式(1)的行波解為 (31) (5)如果ν5(ξ)是式(6)的解,那么式(1)的行波解為 (32) (6)如果ν6(ξ)是式(6)的解,那么式(1)的行波解為 (33) (7)如果ν7(ξ)是式(6)的解,那么式(1)的行波解為 (34) 式(28-30)為孤波解,表示能量在無窮遠衰減的波動現象,類似于量子力學中局域波函數,表示粒子運動的一種局域現象。式(31)是有理解,也在遠處衰減,但是沒有式(28-30)衰減的迅速,表示一種較大范圍的局域效應。式(32-34)是橢圓函數解,表示周期的波動現象。 對于不同的參數,式(1)解的形式是完全不同的。特別是當判別系統的值達到臨界點時,解開始發生分叉現象,從局域運動轉變為周期運動,體現模型豐富的動力學行為。 (35) (36) 當α<0時,式(1)的行波解為 (37) (38) (39) 當w>0時,式(1)的行波解為 (40) (41) 利用多項式完全判別系統法,將(2+1)維廣義Calogero-Bogoyavlenskii-Schiff方程化為積分形式,利用三階多項式完全判別系統,求出方程的所有單行波解的分類,其中包含其他方法沒有得到的新解,如式(32-34)。 在不同等參數條件下解是可以實現的,根據解的分類,對于不同的參數選取,解的形式發生變化,即發生典型的分叉現象,從局域運動到周期運動變化,顯示模型豐富的物理內涵。對于不同的環境條件,模型顯示不同的物理圖像,比一般的動力系統相圖法更簡單直接。 [1] Ablowitz M J, Clarkson P A. Soliton, nonlinear evolution equation and inverse scattering [M]. Cambridge: Cambridge University Press, 1991. [2] 谷超豪.孤立子理論及其應用[M].杭州:浙江科技出版社,1990. Gu Chaohao. Soliton theory and its applications [M]. Hangzhou: Zhejiang Science and Technology Publishing House, 1990. [3] Matveev V B, Salle M A. Darboux transformations and solitons [M]. Berlin: Springer, 1991. [4] Estabrook F B, Wahlquist H D. Prolongation structures of nonlinear evolution equations, Ⅱ [J]. Journal of Mathematical Physics, 1976,17(7):1293-1297. [5] Zhang D G. Integrability of fermionic extensions of the Burgers equation [J]. Physics Letters A, 1996,223(6):436-438. [6] Hereman W, Takaoka M. Solitary wave solutions of nonlinear evolution and wave equations using a direct method and MACSYMA [J]. Journal of Physics A: Mathematical and General, 1990,23(21):4805-4822. [7] Olver P J. Applications of Lie group to differential equation [M]. New York: Springer, 1986. [8] Bluman G W, Kumei S. Symmetries and differential equations [M]. Berlin: Springer, 1989. [9] Parkes E J, Duffy B R. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations [J]. Computer Physics Communications, 1996,98(3):288-300. [10] Liu C S. Exact traveling wave solutions for (1+1)-dimensional dispersive long wave equation [J]. Chinese Physics Society, 2005,14(9):1710-1715. [11] Liu C S. Classification of all single traveling wave solutions to Calogero-Degasperis-Focas equation [J]. Communications in Theoretical Physics, 2007,48(4):601-604. [12] Liu C S. Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations [J]. Computer Physics Communications, 2010,181(2): 317-324. [13] Liu C S. All single traveling wave solutions to (3+1)-Dimensional Nizhnok-Novikov-Veselov equation [J]. Communications in Theoretical Physics, 2006,45(6):991-992. [14] 杜興華.2+1維Bousenisq方程的精確行波解[J].大慶石油學院學報,2007,31(1):118-119. Du Xinghua. Exact traveling wave solutions to (2+1)-dimensional Bousenisq equation [J]. Journal of Daqing Petroleum Institute, 2007,31(1):118-119. [15] Li B, Chen Y. Exact analytical solutions of the generalized Calogero-Bogoyavlenskii-Schiff equation using symbolic computation [J]. Czechos lovak Journal of Physics, 2004,54(5):517-528. [16] 張煥萍,陳勇,李彪.2+1維廣義Calogero-Bogoyavlenskii-Schiff方程的無窮對稱及其約化[J].物理學報,2009,58(11):7393-7396. Zhang Huanping, Chen Yong, Li Biao. Infinitely many symmetries and symmetry reduction of (2+1)-dimensinal generalized Calogero-Bogoyavlenskii-Schiff equation [J]. Acta Physica Sinica, 2009,58(11):7393-7396. [17] 套格圖桑.(2+1)維廣義Calogero-Bogoyavlenskii-Schiff方程的無窮序列類孤子解[J].物理學報,2013,62(21):210201-1-7. Taogetusang. New infinite sequence soliton-like solutions of (2+1)-dimensinal generalized Calogero-Bogoyavlenskii-Schiff equation [J]. Acta Physica Sinica, 2013,62(21):210201-1-7. [18] Bogoyavlenskii O I. Overturning solitons in new two-dimensinal integrable equations [J]. Mathematics of the USSR-lzvestiya, 1990,34(2):245-259. [19] Calogero F. A method to generate solvable nonlinear evolution equations [J]. Lettere al Nuovo Cimento, 1975,14(12):443-447. [20] Schiff J. Integrabillty of Chern-Simons-Higgs vortex equations and a reduction of the Self-Dual Yang-Mills equations to three dimensions [M]//Leri D, Winternitz. Painleve trascendents. New York: Plenum Press, 1992:393-405. 2017-05-02;編輯:任志平 國家自然科學基金項目(11375030) 杜興華(1969-),女,碩士,教授,主要從事數學物理方面的研究。 O192; O189.1 A 2095-4107(2017)03-0111-06 DOI 10.3969/j.issn.2095-4107.2017.03.012
2 單行波解實現
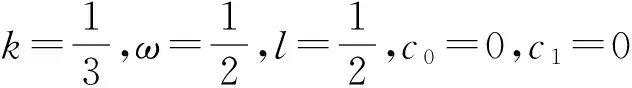
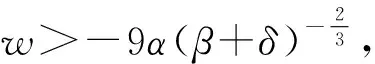
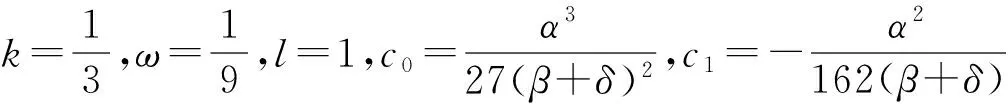
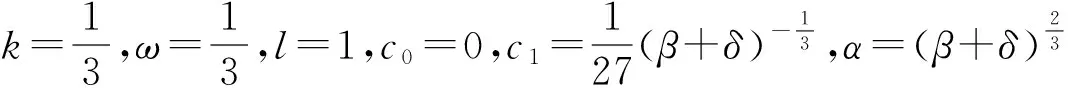
3 結束語

